Kezdőlap


Cím:	Solutions for the Problems of the József Kürschák Mathematics Competition, 2002
Szerző(k):	Gyula Károlyi
Füzet:	2004/februári melléklet, 3 - 13. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Problem 1. The sides of an acute-angled triangle are pairwise different, its orthocentre is $M$ , the centre of its inscribed circle is $K$ , and the centre of its circumscribed circle is $O$ . Prove that if a circle passes through the points $K$ , $O$ , $M$ and a vertex of the triangle, then it also passes through another vertex.

Solution 1. The points

K

O

M

lie in the interior of the triangle. If the vertices are denoted by

A

B

C

and the corresponding angles by

α

β

γ

, then

∠ B A M = 90^{\circ} - β = ∠ C A O

. The second equality is true because in the isosceles triangle

A O C

∠ A O C = 2 β

, since the angle at the centre is twice the angle at the circumference. The line

A K

bisects the angle

B A C

, so the rays

A M

and

A O

lie symmetrically on either side of the ray

A K

. The three rays do not coincide (or else the triangle would be isosceles). Thus the line segments

K M

and

K O

subtend equal angles at the vertex

A

, and the line

A K

separates the points

M

and

O

. It is clear that this statement remains valid if we replace

A

with any other vertex of the triangle.
Assume now that the points

A

M

K

O

are concyclic. Being so, the converse of the theorem about angles at the circumference implies that the line segments

K M

and

K O

are equal. As we have seen, they subtend equal angles at the vertices of the triangle. Let us examine, therefore, the locus of the points

P

where the two edges subtend equal angles.

Figure 1

If that angle is

φ

for a given

P

, then

P

lies on one of the two arcs where the segment

K M

subtends an angle

φ

, and also on one of the two arcs where the segment

K O

subtends an angle

φ

. Let these arcs be

i

and

j

, respectively. We will call the arc

i

an inward arc if the arc lies on the same side of the line

K M

as the point

O

, and an outward arc if they lie on the opposite side. There will be no ambiguity, since the points

K

O

M

cannot be collinear. This terminology can be extended to the arc

j

as well, if we interchange the roles of points

O

and

M

.
If both

i

and

j

are outward arcs, their intersection (if any) lies on the perpendicular bisector

f

of the line segment

M O

, since the two arcs are congruent due to

K M = K O

. The same holds if both arcs are inward ones. The only exception is the case when the two arcs have at least two further common points in addition to their common endpoint

K

. This happens if and only if the two arcs are incident to the same circle, that is the circle through the points

K

O

M

.
Is it possible that we have one outward arc (say, the arc

i

) and one inward arc? In that case, the two arcs intersect each other if and only if

φ

is smaller than the angle

K M O

. Then

j

intersects the extension of the ray

O M

beyond

M

. At that point

K M

and

K O

subtend equal angles, so that point must be the intersection of the two arcs. Such a point, however, cannot be a vertex of the triangle

A B C

, since a circle through that vertex and

K

would not separate the points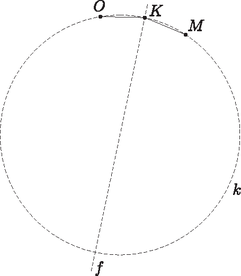

M

and

O

Figure 2

We can conclude that each vertex of the triangle lies either on the line

f

or on the circle

k

. Since the point

K

lies on

f

, at most one of the vertices may lie on

f

, and thus at least two of them must lie on the circle

k

. The claim is hence proved.

Solution 2 (based on the solution by Rácz, Béla András). Let

A

B

C

denote the vertices of the triangle, and assume that the points

A

M

K

O

are on a circle

k

. Note that this circle is unique since the four points are all different. According to the previous solution,

K M = K O

, that is,

K

lies on the perpendicular bisector

f

of the line segment

M O

. Note that the points

B

O

and

M

cannot be collinear, or else

A B

and

B C

would be equal.
Consider the intersection

L

of the angle bisector

e

of the angle

M B O

with the circle

ℓ

circumscribed about the triangle

M B O

. The converse of the theorem about the angles subtended at the circumference of a circle implies

M L = L O

, that is, the point

L

lies on

f

, too. As shown in the first part of the previous proof, the point

K

also lies on the lines

e

and

f

. Therefore, if the lines

e

and

f

do not coincide, then

K = L

, that is, the points

B

O

K

M

all lie on the circle

ℓ

. Since the points

K

O

M

are different,

k

and

ℓ

must be identical, and thus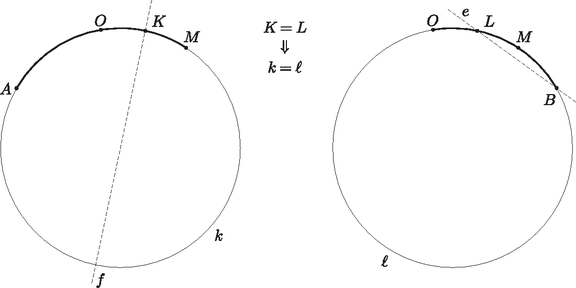

k

passes through the vertex

B

as well.

Figure 3

If the lines

e

and

f

coincide, then

f

passes through the vertex

B

, that is,

B M = B O = R

, where

R

is the radius of the circumcircle of the triangle

A B C

. If

M_{C}

is the perpendicular projection of

M

on the side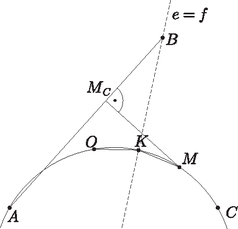

A B

, then

\begin{matrix} B M_{C} = B C cos β = 2 R sin α cos β, \end{matrix}

that is,

\begin{matrix} B M = \frac{B M_{C}}{sin α} = 2 R cos β . \end{matrix}

Thus

cos β = \frac{1}{2}

β = 60^{\circ}

. A simple calculation yields that the edge

A C

subtends a

120^{\circ}

angle at each of the points

M

K

and

O

. Since the points

M

K

O

lie on the same side of the line

A C

, it is the points

A

M

K

O

C

that lie on one circle this time, and that circle must be identical to

k

Figure 4

Solution 3 (based on the solution by Harangi, Viktor). As seen above, the points

K

O

M

are different,

K M = K O

and the line

O M

does not pass through any vertex of the triangle. Assume that the line

O M

separates the vertex

A

from the other two. Then the perpendicular bisector

f

of the line segment

O M

(which passes through the point

K

) must intersect the side

B C

, otherwise one of the points

M

and

O

(say,

M

) would lie closer to each of the points

B

and

C

than the other one. Since

K

lies on both the bisector of the angle

M B O

and that of the angle

M C O

, and an angle bisector divides the opposite side in the ratio of the adjacent sides, it follows that both of the lines

B K

and

C K

would intersect the line segment

O M

closer to its endpoint

M

, and thus

K

would also lie closer to

M

than

O

. That is contradiction.
Thus one of the vertices

B

and

C

lies on the same side of the line

f

as the point

M

, and the other one lies on the same side as

O

. Without loss of generality, we may assume that

B M \leq B O

and

C M \geq C O

, where at least one of these relations is a strict inequality. Therefore the line

B K

intersects the line segment

M O

closer to

M

, and the line

C K

intersects it closer to

O

. (One, but not both of the intersections may coincide with the midpoint of the edge

M O

). Consequently, the line

O M

separates the point

K

from the vertices

B

and

C

. We can establish, therefore, that both vertices

B

and

C

lie between the arms of the angle

M K O

.
Reflect now the point

C

in the line

f

to get the point

C'

. Since

∠ K C' O = ∠ K C M = ∠ K C O

, and

C

and

C'

are on the same side of the line

K O

, the points

K

C

C'

O

are clearly concyclic, and for symmetry reasons their circle also passes through the point

M

. Thus

C

lies on the circumscribed circle of the triangle

K O M

. For the same reason, vertex

B

is also incident to this circle but vertex

A

is not, since the line

M O

does not separate the points

A

and

K

. That completes the proof.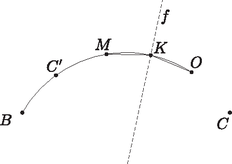

Figure 5

Remarks. Is it a necessary condition that the sides of the triangle are pairwise different? If the triangle is isosceles, then the points

K

O

M

are collinear. A circle can pass through all these points only if two of them coincide, that is, if the triangle is equilateral. Thus it would have been enough to require that the triangle is a non-equilateral acute-angled triangle.
If the triangle is not acute-angled, it cannot be equilateral either, and such a restriction is not needed. If the triangle is right-angled, the point

M

coincides with a vertex. Thus if a circle passes through the points

K

O

M

, then it necessarily passes through a vertex of the triangle. However, it can pass through another vertex only if the third angle is

60^{\circ}

. (Why?) The statement is hence not true for right triangles. And what about an obtuse triangle? In that case the solution is more complicated, but the claim still holds.

Exercises
1) The orthocentre of an obtuse-angled triangle is

M

, the centre of its inscribed circle is

K

, and the centre of its circumscribed circle is

O

. Prove that if a circle passes through the points

K

O

M

and a vertex of the triangle, then it also passes through another vertex.
2) If a triangle is not right-angled, then there exists a circle passing through the points

K

O

M

and a vertex if and only if one angle of the triangle is

60^{\circ}

Problem 2. Consider the sequence of the Fibonacci numbers defined by the recursion

\begin{matrix} f_{1} = f_{2} = 1, f_{n} = f_{n - 1} + f_{n - 2} (n \geq 3) . \end{matrix}

Assume that the fraction

\frac{a}{b}

, where

a

and

b

are positive integers, is smaller than one of the fractions

\frac{f_{n}}{f_{n - 1}}

and

\frac{f_{n + 1}}{f_{n}}

but is greater than the other. Show that

b \geq f_{n + 1}

Solution 1 (based on the solutions by Kocsis, Albert Tihamér and Zsbán, Ambrus). The proof is by induction on

n

. Let us check the claim first for

n = 2

and

3

. For

n = 2

, the condition is

1 < \frac{a}{b} < 2

, and hence

b \geq 2 = f_{3}

. For

n = 3

\frac{3}{2} < \frac{a}{b} < 2

implies

b \geq 3 = f_{4}

. Assume now that

m \geq 3

and the statement is already proved for

2 \leq n \leq m

.
Let

n = m + 1

, and assume that

\frac{f_{n}}{f_{n - 1}} < \frac{f_{n + 1}}{f_{n}}

, and the positive integers

a

and

b

satisfy

\begin{matrix} \frac{f_{m + 1}}{f_{m}} = \frac{f_{n}}{f_{n - 1}} < \frac{a}{b} < \frac{f_{n + 1}}{f_{n}} = \frac{f_{m + 2}}{f_{m + 1}} . \end{matrix}

Reducing the terms in the inequality by 1, we get

\begin{matrix} \frac{f_{m - 1}}{f_{m}} = \frac{f_{m + 1} - f_{m}}{f_{m}} < \frac{a - b}{b} < \frac{f_{m + 2} - f_{m + 1}}{f_{m + 1}} = \frac{f_{m}}{f_{m + 1}} . \end{matrix}

Since there are positive numbers at both ends (and thus in the middle as well), the inequality is reversed when switching to the reciprocals:

\begin{matrix} \frac{f_{m}}{f_{m - 1}} > \frac{b}{a - b} > \frac{f_{m + 1}}{f_{m}} . \end{matrix}

It follows from the assumption that

a - b \geq f_{m + 1}

. If the terms are reduced by 1 once more and the reciprocals are taken, the inequality

\begin{matrix} \frac{f_{m - 1}}{f_{m - 2}} < \frac{a - b}{2 b - a} < \frac{f_{m}}{f_{m - 1}} \end{matrix}

is obtained, and then it follows from the assumption that

2 b - a \geq f_{m}

.
Adding the two results yields

\begin{matrix} b = (2 b - a) + (a - b) \geq f_{m} + f_{m + 1} = f_{m + 2} = f_{n + 1}, \end{matrix}

thus the statement is true for

n = m + 1

.
The same reasoning applies when

\begin{matrix} \frac{f_{m + 1}}{f_{m}} = \frac{f_{n}}{f_{n - 1}} > \frac{a}{b} > \frac{f_{n + 1}}{f_{n}} = \frac{f_{m + 2}}{f_{m + 1}}, \end{matrix}

only one should interchange the roles of the relations ``

<

'' and ``

>

''.

Solution 2 (based on the solution by Egri, Attila). Let us assume that

\begin{matrix} \frac{f_{n}}{f_{n - 1}} < \frac{a}{b} < \frac{f_{n + 1}}{f_{n}} . \end{matrix}

Multiplying through the inequality by the positive quantity

b f_{n - 1} f_{n}

we get

\begin{matrix} b f_{n}^{2} < a f_{n - 1} f_{n} < b f_{n - 1} f_{n + 1} . \end{matrix}

The difference between the first two numbers is

f_{n} \cdot (a f_{n - 1} - b f_{n})

, a positive integer divisible by

f_{n}

, whose value is therefore at least

f_{n}

. For similar reasons, the difference

f_{n - 1} \cdot (b f_{n + 1} - a f_{n})

between the last two numbers is at least

f_{n - 1}

. Therefore the difference between the first and last numbers is:

\begin{matrix} b (f_{n - 1} f_{n + 1} - f_{n}^{2}) \geq f_{n} + f_{n - 1} = f_{n + 1} . \end{matrix}

Hence it is enough to prove that

k_{n} = f_{n - 1} f_{n + 1} - f_{n}^{2} = 1

.
If

n = 2

then

k_{n} = 1

, and if

n = 3

then

k_{n} = - 1

. If we go on checking the values of

k_{n}

, we find alternating values of

+ 1

and

- 1

, that is,

k_{n} = {(- 1)}^{n}

. This is true for

n = 2

, and if it holds for some integer

n \geq 2

, then it follows that

\begin{matrix} \begin{matrix} k_{n + 1} & = f_{n} f_{n + 2} - f_{n + 1}^{2} = f_{n} (f_{n} + f_{n + 1}) - f_{n + 1}^{2} \\ = f_{n}^{2} - f_{n + 1} (f_{n + 1} - f_{n}) = f_{n}^{2} - f_{n + 1} f_{n - 1} = - k_{n} = - {(- 1)}^{n} = {(- 1)}^{n + 1} . \end{matrix} \end{matrix}

Since in our case

b

and

f_{n + 1}

are both positive,

k_{n}

must also be positive and thus its value is 1, as we set out to prove. A similar argument works if

\begin{matrix} \frac{f_{n}}{f_{n - 1}} > \frac{a}{b} > \frac{f_{n + 1}}{f_{n}} . \end{matrix}

Remark. This argument also yields the general statement that if

a

b

x

y

z

v

are positive integers,

y z - x v = 1

and

\frac{x}{y} < \frac{a}{b} < \frac{z}{v}

, then

b \geq y + v

Solution 3. Assume for simplicity that

n

is even. According to the relation

f_{n - 1} f_{n + 1} - f_{n}^{2} = {(- 1)}^{n}

used in the previous solution, the inequality

\begin{matrix} \frac{f_{n}}{f_{n - 1}} < \frac{a}{b} < \frac{f_{n + 1}}{f_{n}} \end{matrix}

holds in this form. The difference

\begin{matrix} \frac{a}{b} - \frac{f_{n}}{f_{n - 1}} = \frac{a f_{n - 1} - b f_{n}}{b f_{n - 1}} \end{matrix}

is positive, so being an integer, the numerator is at least 1. Therefore,

\begin{matrix} \frac{1}{b f_{n - 1}} \leq \frac{a}{b} - \frac{f_{n}}{f_{n - 1}} < \frac{f_{n + 1}}{f_{n}} - \frac{f_{n}}{f_{n - 1}} = \frac{1}{f_{n - 1} f_{n}}, \end{matrix}

and hence

b f_{n - 1} > f_{n - 1} f_{n}

, that is,

b > f_{n}

.
Consider the fraction

\frac{f_{n + 2}}{f_{n + 1}}

which is smaller than

\frac{f_{n + 1}}{f_{n}}

. If

\begin{matrix} \frac{f_{n + 2}}{f_{n + 1}} < \frac{a}{b} < \frac{f_{n + 1}}{f_{n}}, \end{matrix}

then a reasoning similar to the one above yields

\begin{matrix} \frac{1}{b f_{n}} \leq \frac{f_{n + 1}}{f_{n}} - \frac{a}{b} < \frac{f_{n + 1}}{f_{n}} - \frac{f_{n + 2}}{f_{n + 1}} = \frac{1}{f_{n + 1} f_{n}}, \end{matrix}

and therefore

b > f_{n + 1}

.
If

\frac{a}{b} = \frac{f_{n + 2}}{f_{n + 1}}

, then

b \geq f_{n + 1}

for

f_{n + 2}

and

f_{n + 1}

are relatively prime. This is shown as follows: if a positive integer

d

divides both

f_{n + 2}

and

f_{n + 1}

, then it also divides their difference

f_{n} = f_{n + 2} - f_{n + 1}

, and so on,

d

divides all the numbers

f_{n - 1}, f_{n - 2}, ..., f_{1}

. Since

f_{1} = 1

d

must be 1.
There remains the case

\begin{matrix} \frac{f_{n}}{f_{n - 1}} < \frac{a}{b} < \frac{f_{n + 2}}{f_{n + 1}} . \end{matrix}

Consider the difference

ℓ_{n} = f_{n + 2} f_{n - 1} - f_{n} f_{n + 1}

. By induction we get

ℓ_{n} = {(- 1)}^{n}

, and therefore

\begin{matrix} \frac{1}{b f_{n - 1}} \leq \frac{a}{b} - \frac{f_{n}}{f_{n - 1}} < \frac{f_{n + 2}}{f_{n + 1}} - \frac{f_{n}}{f_{n - 1}} = \frac{1}{f_{n + 1} f_{n - 1}}, \end{matrix}

and again we can conclude that

b > f_{n + 1}

.
A similar argument yields the claim if

n

is odd.

Several papers used the theory of the Farey sequence. Here is an example.

Solution 4. (based on the solution by Pallos, Péter). Starting from the sequence

F_{1} = (\frac{0}{1}, \frac{1}{1})

, proceed using the following recurrence. Having defined the sequence

F_{n}

, insert the fraction

\frac{a + c}{b + d}

between any two consecutive terms

\frac{a}{b}

and

\frac{c}{d}

F_{n}

. If the sequence

F_{n}

is strictly increasing, then so is the next sequence

F_{n + 1}

. The solution is based on the following two theorems: 1. Each fraction appears in the sequence

F_{n}

in lowest terms. 2) Every rational number between

0

and

1

belongs to some sequence

F_{n}

.
Note that

\frac{f_{n - 1}}{f_{n}}

and

\frac{f_{n}}{f_{n + 1}}

are consecutive terms of the sequence

F_{n}

. This is the case if

n = 2

, and if

\frac{f_{n - 1}}{f_{n}}

and

\frac{f_{n}}{f_{n + 1}}

are consecutive terms of

F_{n}

for an integer

n \geq 2

, then the fraction inserted between them in the next sequence

F_{n + 1}

is equal to

\begin{matrix} \frac{f_{n - 1} + f_{n}}{f_{n} + f_{n + 1}} = \frac{f_{n + 1}}{f_{n + 2}}, \end{matrix}

therefore the statement is also true for

n + 1

.
Since

f_{n}

is strictly increasing, the fraction

\frac{a}{b}

is greater than 1. According to the above properties, the fraction

\frac{b}{a}

thus occurs in some sequence

F_{m}

, reduced to lowest terms in a form

\frac{b'}{a'}

. Since

\frac{b'}{a'}

is greater then one of the fractions

\frac{f_{n - 1}}{f_{n}}

and

\frac{f_{n}}{f_{n + 1}}

and smaller than the other one, clearly

m > n

. The construction of the sequences

F_{m}

implies that the numerator of every fraction inserted between

\frac{f_{n - 1}}{f_{n}}

and

\frac{f_{n}}{f_{n + 1}}

is at least

f_{n - 1} + f_{n}

, and hence

\begin{matrix} b \geq b' \geq f_{n - 1} + f_{n} = f_{n + 1} . \end{matrix}

The proof is hence complete.

Remark. In this solution, a sledgehammer was used to crack a nut, since the proofs of the stated properties of Farey sequences are actually based on considerations contained in the previous solutions.

Problem 3. Prove that the set of edges formed by the sides and diagonals of a convex

3^{n}

-gon can be partitioned into sets of three edges, such that the edges in each triple form a triangle.

Solution 1 (based on the solution by Csikvári, Péter). Let us assign to the vertices of the polygon the numbers

0,1,2, ..., 3^{n} - 1

, written in base-3 notation. Each number consists of

n

digits at most. If the number of digits is less than

n

, then adding leading zeros we have a sequence of

n

digits of 0, 1 or 2. In other words, we assign to the vertices of the polygon those sequences of length

n

whose terms are either 0, 1, or 2.
Consider the triangles satisfying the following condition: Whichever position is chosen from the first to the

n

-th, the three numbers assigned to the vertices of the triangle either have the same digit at the given position, or all three of them have different digits at that position. It is clear that for any pair of vertices of the polygon there is exactly one additional vertex available such that the three of them satisfy the above condition. Thus every single side and diagonal of our polygon is the side of exactly one such triangle, and hence the sets of three edges forming the sides of such triangles will have the required property.

Solution 2. The proof is by induction on

n

. The claim is obvious if

n = 1

. Assume that the statement is already proved for some positive integer

n

and consider a convex

3^{n + 1}

-gon whose vertices are

A_{i}

B_{i}

C_{i}

where

1 \leq i \leq 3^{n}

. By the induction hypothesis the edges connecting the vertices

A_{i}

can be divided into triplets as required. The same is true for the edges connecting the vertices

B_{i}

and for those connecting the vertices

C_{i}

.
The rest of the edges can be grouped as follows: The edges

A_{i} B_{j}

B_{j} C_{k}

and

C_{k} A_{i}

are put together whenever

i + j + k

is divisible by

3^{n}

. It is clear that three such edges form a triangle. On the other hand, if any two of the numbers

i

j

k

are fixed, the divisibility condition uniquely determines the third one, and hence every edge occurs in exactly one triplet. The statement is hence true for

n + 1

, and the induction step is complete.

Solution 3 (based on the solution by Steller, Gábor). As in the previous solutions, the task is to find triangles such that their vertices are vertices of the original polygon, and each given edge is a side of one and only one triangle. In other words, any pair of triangles have at most one vertex in common. We also use mathematical induction to prove that this can be done. Assume that we have found suitable triangles

P_{i} P_{j} P_{k}

for a polygon

P_{1} P_{2} ... P_{3^{n}}

. It follows from the conditions that the number of triangles is one third of the total number of edges, that is,

\begin{matrix} \frac{1}{3} (\binom{3^{n}}{2}) = \frac{3^{n - 1} (3^{n} - 1)}{2} . \end{matrix}

Let

A_{i}

B_{i}

C_{i}

(

1 \leq i \leq 3^{n}

) denote the vertices of a convex

3^{n + 1}

-gon. Consider the triangles

A_{i} B_{i} C_{i}

where

1 \leq i \leq 3^{n}

, and call them triangles of the first kind. Consider now each triangle

P_{i} P_{j} P_{k}

of the above partition, and construct the triangles

A_{i} A_{j} A_{k}

B_{i} B_{j} B_{k}

C_{i} C_{j} C_{k}

(second kind) and the triangles

A_{i} B_{j} C_{k}

A_{i} C_{j} B_{k}

B_{i} A_{j} C_{k}

B_{i} C_{j} A_{k}

C_{i} A_{j} B_{k}

C_{i} B_{j} A_{k}

(third kind). One gets

\begin{matrix} 9 \cdot \frac{3^{n - 1} (3^{n} - 1)}{2} + 3^{n} = \frac{3^{n} (3^{n + 1} - 3)}{2} + 3^{n} = \frac{3^{n} (3^{n + 1} - 1)}{2} \end{matrix}

triangles altogether, which is equal to the number of triangles needed for a suitable partition. Therefore, it is enough to show that any pair of triangles listed above have at most one vertex in common.
It is clear that triangles of the first kind have no vertex in common at all, and they cannot have more than one common vertex with any triangle of the second kind either. Two triangles of the second kind either have no common vertex, or by the induction hypothesis they have at most one such vertex. Triangles of the third kind may have at most one vertex in common with triangles of the other two kinds. Finally, two triangles of the third kind may have at most one common vertex. This follows from the induction hypothesis, since if, say,

A_{i} B_{j} C_{k}

and

A_{i} B_{j} C_{k'}

are both triangles of the third kind, then the partition of the original

3^{n}

-gon must have contained both the triangles

P_{i} P_{j} P_{k}

and

P_{i} P_{j} P_{k'}

. That can only happen if

k = k'

Solution 4 (based on the solution by Harangi, Viktor). We can assume without the loss of generality that the polygon is regular. This opens the way for a geometric argument. The solution is once again by induction on

n

. For

n = 1

, the statement is trivial. Assume that the problem is already solved for some

n \geq 1

, and consider a regular

3^{n + 1}

-gon

P

. Label the vertices with the three letters

A

B

C

, going around the polygon in some direction. Vertex

A

is always followed by

B

, then

C

and then

A

again. The vertices labelled identically form three

3^{n}

-gons, and the edges of each can be partitioned as required. There remains to take care of the edges connecting differently labelled vertices.
Consider the symmetry axis

t

of the polygon through a vertex marked

A

. Since

P

has an odd number of vertices, this axis does not contain any other vertex. The image after a reflection of a vertex marked

A

about the axis

t

is another vertex marked

A

, that of a reflection of a vertex marked

B

is a vertex marked

C

, and that of a reflection of a vertex marked

C

is a vertex marked

B

. Similarly, if the axis is through a vertex marked

B

C

, it is the vertices marked

B

and

C

, respectively, that map onto vertices of the same kind.
We proceed now as follows: the edges of a triangle of type

A B C

are grouped together if and only if the triangle is symmetrical about the axis of the polygon passing through the vertex

A

. We show that every edge of type

A B

B C

C A

of the polygon

P

is used exactly once, which means that the induction works.
An edge of type

A B

belongs exactly to one such triangle, the one whose third vertex is obtained by reflecting

B

about the axis through

A

. The image will be a vertex of type

C

as said above. By symmetry, each edge of type

A C

belongs to exactly one triangle as well. Finally, consider an edge of type

B C

. Its perpendicular bisector is a symmetry axis of

P

, so it passes through a particular vertex of

P

, which must be a vertex of type

A

for the reasons mentioned above. That vertex, and only that may be the third vertex of the required triangle.

Finally, let us examine the solution that reveals the genuine geometrical (or algebraic, if you like) background of the problem. The required partition can be accomplished in terms of the lines of the

n

-dimensional affine space over the three-element field. The argument below will hopefully reveal the point of the story.

Solution 5 (based on the solution by Rácz, Béla András). Let

p

be an arbitrary prime number. We are going to prove the following general theorem: The edges of a complete graph on

p^{n}

vertices can be partitioned into sets forming the edges of a complete graph on

p

points each. For

p = 3

, this is simply the original problem. See on the front page.
Consider the sequences

a = (a_{1}, a_{2}, ..., a_{n})

where, for every

i

a_{i}

is a non-negative integer less than

p

. The number of such sequences is clearly

p^{n}

. They represent the points of the

n

-dimensional affine space over the

p

-element field, which we will identify with the vertices of the given complete graph. We may also think of them as vectors, similar to the way the position vectors are identified with their endpoints in 3-dimensional Euclidean space. The sum of two points

a

and

v

is defined as

\begin{matrix} a + v = (a_{1} + v_{1}, a_{2} + v_{2}, ..., a_{n} + v_{n}), \end{matrix}

where the sums

a_{i} + v_{i}

are meant modulo

p

. We can also say that the point

a

is shifted by the vector

v

. The difference between two points can be defined in a similar way, and

a + (b - a) = b

will be true.

α

times a point (or vector)

v

is defined as the point (or vector)

\begin{matrix} α v = (α v_{1}, α v_{2}, ..., α v_{n}), \end{matrix}

where

α \in {0,1, ..., p - 1}

and

α v_{i}

is also considered modulo

p

. If the integers

α

and

β

are congruent modulo

p

α v

and

β v

define the same point.
How can we define a line through two different points

a

and

b

? Let us add the multiples of the vector

v = b - a

to the point

a

, as we would do in the Euclidean case. It is easy to show that any such line consists of

p

distinct points. On one hand, there may be at most

p

points on the line since it is enough to add the vector

v

to the point

a

0,1, ..., p - 1

times. On the other hand, if

a + j v = a + k v

for two different numbers

j, k \in {0,1, ..., p - 1}

then

j v_{i} = k v_{i}

modulo

p

for each coordinate

v_{i}

v

. Thus

(k - j) v_{i}

is divisible by

p

, which can only happen if every

v_{i}

is zero. That contradicts

a

and

b

being different points.
Any pair of distinct points determine a line passing through exactly

p

points. The crucial observation is that any pair of different lines have at most one point in common, or in other words, any pair of points belong to exactly one line. Hence the statement follows: the complete graphs on

p

points to be found correspond to the different lines.

Exercises
1) Prove that the roles of

a

and

b

can be interchanged in the definition of the line through

a

and

b

.
2) Prove that if

c = a + α (b - a)

and

d = a + β (b - a)

are two different points of the line through the points

a

and

b

, then

a

and

b

lie on the line determined by

c

and

d

. How does this imply the ``crucial'' observation mentioned in the solution?
3) How can we define two lines to be parallel?
4) How can planes be defined? How many points will a plane have? What would the set of common points of two planes look like?
5) What problems would we face if, formulating the statement of the above general theorem with a composite number

m

in the place of the prime

p

, we tried to apply the same ideas to obtain a proof?