Kezdőlap


Cím:	The 2003 Eötvös Competition
Szerző(k):	Gnädig Péter
Füzet:	2004/januári melléklet, 42 - 48. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

On 17 October 2003 Eötvös Loránd Physical Society held in Budapest and in 15 other towns the 55th Eötvös Competition since the 1949 restart of the event.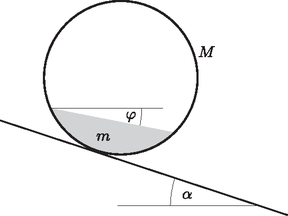
In the following we present the problems and their solution.

1. A thin-walled cylinder rolls without slipping down a slope with incline angle of

α = 10^{\circ}

. The mass of the cylinder wall is

M

and the mass of the closing disks is negligible. The cylinder contains mercury of mass

m

. (The friction between the cylinder and the mercury is negligible.)

Figure 1

The sloping angle of the mercury surface settles at some angle

φ

. Determine this angle

φ

a)

M ≪ m;

b)

M = m .

(Péter Balogh)

Solution. The solution based on dynamics seems straightforward. Force is exerted on the mercury by the Earth and by the cylinder. On the cylinder there is force exerted by the Earth, the mercury and the slope. Therefore force is exerted on this system (mercury + cylinder) by the slope and the Earth. As a result the mass centre of the system moves parallel with the slope with an acceleration of

a

. Denoting the friction force by

S

, by the law of dynamics (second law of motion):

\begin{matrix} (m + M) g sin α - S = (m + M) a . \end{matrix}

The cylinder rotates around its mass centre, which is also moving, with an angular acceleration of

β = a / R

. The accelerated rotation is driven by friction force

S

. (Note that the mercury does not rotate since the friction is negligible between the mercury and the cylinder.) Therefore the dynamical equation is: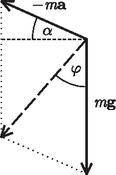

\begin{matrix} S R = M R^{2} \frac{a}{R}, \end{matrix}

from where

\begin{matrix} S = M a \end{matrix}

follows. Substituting this into the dynamical equation of the motion for the acceleration we get

\begin{matrix} a = \frac{m + M}{m + 2 M} g sin α . \end{matrix}

In special cases

\begin{matrix} a = {\begin{matrix} g sin α, & if M ≪ m; \\ \frac{2}{3} g sin α, & if M = m; \\ \frac{1}{2} g sin α, & if M ≫ m . \end{matrix} \end{matrix}

The simplest way we can determine the sloping angle of the mercury is if we consider that in a system co-accelerating with the liquid, the surface of the liquid is still perpendicular to the resultant force of the gravitational and inertial forces acting on it. The angle

φ

between the surface of the mercury and the horizontal plane will be the same as the angle

φ

between the resultant force and the vertical direction. On the basis of Figure 2 the tangent of the angle in question is easily given by

\begin{matrix} tan φ = \frac{m a cos α}{m g - m a sin α} = \frac{cos α}{\frac{g}{a} - sin α} . \end{matrix}

Figure 2

Let us examine the three special cases concerning acceleration.

a)

When

M ≪ m

\begin{matrix} tan φ = \frac{cos α}{\frac{1}{sin α} - sin α} = tan α, \end{matrix}

that is

φ = α = 10^{\circ}

b)

When

M = m

\begin{matrix} tan φ = \frac{cos α}{\frac{3}{2 sin α} - sin α} = \frac{2 sin α cos α}{3 - 2 sin^{2} α}, \end{matrix}

from where

φ = 6. 636^{\circ} \approx 6. 6^{\circ}

c)

In the case of

M ≫ m

\begin{matrix} tan φ = \frac{cos α}{\frac{2}{sin α} - sin α} = \frac{sin α cos α}{2 - sin^{2} α}, \end{matrix}

from where

φ = 4. 962^{\circ} \approx 5. 0^{\circ}

Note. The discussion of the

M ≫ m

case was not in the original objectives of the problem. It is discussed here simply for the sake of symmetry and because some of the competitors examined this instead of the

M ≪ m

case.

2. In two infinitely thin linear conductors situated parallel at a distance

d

from each other electric currents of the same magnitude flow in opposite directions. The lines of magnetic induction are in planes perpendicular to the conductors. Choose an arbitrary point

P

in one of the planes and examine whether the induction line going through that point is circular.

(Gyula Radnai)

Solution. Figure 3 illustrates some of the magnetic induction lines of the magnetic field generated by the currents in the two parallel conductors equal in magnitude but of opposite directions.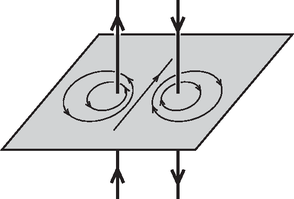

Figure 3

Due to the special current pattern the resulting magnetic field shows considerable symmetry. The induction lines separating the two conductors are not only mirror images of each other but any closed line following the direction of magnetic induction is also symmetric to the plane laid across the two conductors. This does not mean that the induction lines cannot be ellipses or higher order closed curves, but if there is a circle among them, its center must be situated in the plane laid across the conductors.
Let us define an

(x, y)

coordinate system in the selected plane in a way that one of the currents crosses it in the origin, and the other at point

(d,0)

. Only those circles containing point

P (x, y)

of the plane can be real induction lines that have their center on axis ``

x

''. The center of the circle is

(x_{0},0)

. The equation of the circle is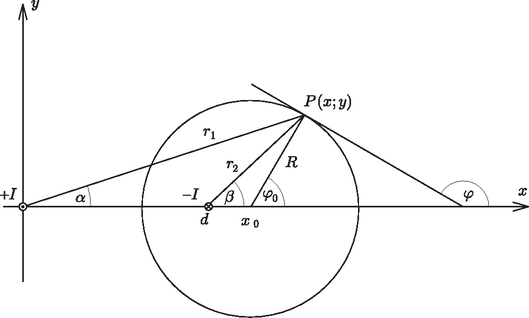

\begin{matrix} {(x - x_{0})}^{2} + y^{2} = R^{2}, \end{matrix}

where

R

is a function of

d

and

x_{0}

Figure 4

If this circle is an induction line, then at any point of the circle the direction of the induction vector is the same as that of the tangent line at that point (Figure 4). The angular coefficient at point

P (x, y)

\begin{matrix} tan φ = - \frac{1}{tan φ_{0}} = - \frac{1}{\frac{y}{x - x_{0}}} = - \frac{x - x_{0}}{y} . \end{matrix}

This is to be compared with the angular coefficient of the induction vector in point

P

. The angular coefficient of the resultant

B

is (Figure 5)

\begin{matrix} tan φ_{B} = \frac{B_{y}}{B_{x}} = \frac{B_{1 y} + B_{2 y}}{B_{1 x} + B_{2 x}} . \end{matrix}

Let us calculate this quantity. The magnitude of the induction vector generated by a single conductor is

\begin{matrix} B = \frac{μ_{0} I}{2 π} \cdot \frac{1}{r} . \end{matrix}

With this and exploiting the geometrical properties shown in Figure 5 the individual components are

\begin{matrix} B_{1 y} & = & B_{1} cos α = \frac{μ_{0} I}{2 π} \cdot \frac{cos α}{r_{1}} = \frac{μ_{0} I}{2 π} \cdot \frac{x}{r_{1}^{2}}, \\ B_{2 y} & = & - B_{2} cos β = - \frac{μ_{0} I}{2 π} \cdot \frac{cos β}{r_{2}} = \frac{μ_{0} I}{2 π} \cdot \frac{(d - x)}{r_{2}^{2}}, \\ B_{1 x} & = & - B_{1} sin α = - \frac{μ_{0} I}{2 π} \cdot \frac{sin α}{r_{1}} = - \frac{μ_{0} I}{2 π} \cdot \frac{y}{r_{1}^{2}}, \\ B_{2 x} & = & B_{2} sin β = \frac{μ_{0} I}{2 π} \cdot \frac{sin β}{r_{2}} = \frac{μ_{0} I}{2 π} \cdot \frac{y}{r_{2}^{2}} . \end{matrix}

Let us substitute these expressions into the the equation set up for

tan φ_{B}

. After reduction we get

\begin{matrix} tan φ_{B} = \frac{\frac{x}{r_{1}^{2}} + \frac{d - x}{r_{2}^{2}}}{- \frac{y}{r_{1}^{2}} + \frac{y}{r_{2}^{2}}} = \frac{x (\frac{1}{r_{1}^{2}} - \frac{1}{r_{2}^{2}}) + \frac{d}{r_{2}^{2}}}{- y (\frac{1}{r_{1}^{2}} - \frac{1}{r_{2}^{2}})} = - \frac{x - \frac{d}{1 - {(r_{2} / r_{1})}^{2}}}{y} . \end{matrix}

This expression can be equivalent to the earlier expression

\begin{matrix} tan φ = - \frac{x - x_{0}}{y} \end{matrix}

if and only if

\begin{matrix} x_{0} = \frac{d}{1 - {(r_{2} / r_{1})}^{2}} . \end{matrix}

Substituting also expressions

r_{2} = \sqrt[]{y^{2} + {(x - d)}^{2}}

and

r_{1} = \sqrt[]{y^{2} + x^{2}}

after rearranging the sides we get

{(x - 0)}^{2} + y^{2} = x_{0} (x_{0} - d)

. And this is exactly the equation of the

(x_{0},0)

centered circle containing the given point

P

, that is the induction line is circular. We get the radius of the circle as well

\begin{matrix} R = \sqrt[]{x_{0} (x_{0} - d)} . \end{matrix}

Figure 5

Since

P

can be any point in space and across one point there can go only one line, in this magnetic field every induction line is circular!

Note. The loci of the points of the plane with constant ratio of distances from two given points is the so called Apollonius' circle. Our results can be interpreted in other words that the induction lines of this magnetic field are Apollonius' circles.

Introducing the notation

r_{2} / r_{1} = λ

, the equation of the circles becomes

\begin{matrix} {(x - \frac{d}{1 - λ^{2}})}^{2} + y^{2} = {(λ \frac{d}{1 - λ^{2}})}^{2}, \end{matrix}

from where the interesting relationship

R = λ x_{0}

can also be read. (Apollonius lived between 262 and 190 b.c., and he introduced the terms ellipse, parabola and hyperbola in his work on conic sections.)

3. Inside the capsule of a freely orbiting spaceship a water ball

4 cm

in diameter is floating motionless. In its vicinity there is a

8 cm

long thin glass stick of circular cross-section with rounded ends. We gently make the stick touch the ``water drop''. Outline what shape the water is going to take.

(Frigyes Károlyházy)

Solution. At the beginning (Figure 6) the glass stick floats in the vicinity of the water ball.
The process begins when we gently touch the water drop with one end of the stick (Figure 7). The water moistens the stick, slightly flowing onto the rounded end of the stick (Figure 8). However, the process cannot stop here since the resultant force acting on the stick is not zero. It is true that the pressure is somewhat higher inside the water drop than the air pressure outside (

Δ p = 2 α / R

) and this could result in pushing the stick of radius

r

outwards, but the

2 r π α

suction force of the water film covering the stick is much larger. Therefore, the stick advances further into the water drop. This intermediate situation is shown in Figure 9.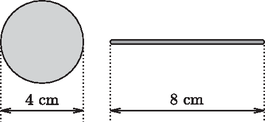

Figure 6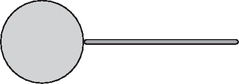

Figure 7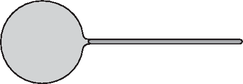

Figure 8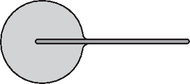

Figure 9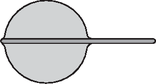

Figure 10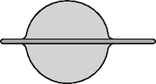

Figure 11

But there is still no equilibrium of forces, there is no reason why the stick should stop until the state shown in Figure 10. Here the stick reaches the left side of the water drop and slightly overshoots so the water surface is slightly extruded. The equilibrium of forces is reached only when the left end of the stick emerges from the water drop and the water surface at both ends of the stick takes the same shape (Figure 11).
It is also to be considered whether the water drop spreads on the stick or not. The total energy of the system equals the sum of the surface energy of the water touching the air and the surface energy of the water touching the glass. This energy tries to be the smallest possible. Considering that the stick is thin, the amount of glass surface is negligible compared to the overall surface of the water ball. The equilibrium of the system is determined by the minimum surface requirement of the water, and this is met by the shape of a sphere (in the case of constant volume). In the final state the water ball is almost exactly spherical, and the glass stick lies in the diameter of the sphere with both of its ends sticking out from the water.

*

The ceremonial declaration of the results took place on 21 November 2003.
First the president of the competition committee spoke in memory of the late Ede Teller and recited the problems that Teller had to solve to win the 1925 Eötvös competition. The people present agreed that those problems were easier than the current ones. It is to be admitted though that at that time not too much literature, not as many good exercise books and clubs were available for preparation.
After the introductory flashbacks, the presentation of the 2003 Eötvös competition problems and their correct solutions followed. To the solutions of the first two problems given by Gyula Radnai, Peter Gnädig added some interesting supplementary notes and presented a solution based on a surprising analogy. Then the president of the competition committee asked some of the best performing participants to present their solutions of the third problem approached from different angles.
The prizes were handed to the winners by Judit Németh, corresponding member of the Hungarian Academy of Sciences and president of the Loránd Eötvös Physical Society.
The first prize along with a 20000Ft book certificate was awarded to Márton Horváth 12th grade student of Fazekas Mihály Secondary School, Budapest, pupil of Gábor Horváth. He correctly solved all the three problems.
The second prize with a 15000Ft book certificate was awarded each to Endre Csóka, a mathematics student of Eötvös Loránd University, who formerly passed his A levels at Fazekas Mihály Secondary School, Debrecen as pupil of Ervin Szegedi and to Péter Kómár 11th grade student of Fazekas Mihály Secondary School, Budapest, pupil of Cecília Dvorák.
The happiest competitor this year again was the first prize winner, because besides the moral victory he was also awarded the Society's Eötvös Competition Medal. Thus there are already two people in the country who possess this medal.