Kezdőlap


Cím:	Solutions to the Problems of the József Kürschák Mathematics Competition
Szerző(k):	Tamás Fleiner
Füzet:	2005/februári melléklet, 13 - 18. oldal	PDF \| MathML

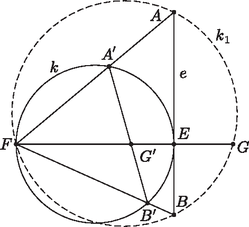
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Problem 1. The line $e$ touches the circle $k$ of diameter $E F$ at the point $E$ . Consider all point pairs $A$ , $B$ of the line $e$ , such that the line segment $A B$ contains the point $E$ and $A E \cdot E B$ equals a given constant. For such a pair of points, let $A'$ and $B'$ denote the intersections of the circle $k$ with the line segments $A F$ and $B F$ , respectively. Prove that the lines $A' B'$ are all concurrent.

Solution 1. Let

G

denote the second intersection of the circle

k_{1}

circumscribed about the triangle

A B F

and the line

E F

. The power of the point

E

with respect to

k_{1}

is a constant (

A E \cdot E B = F E \cdot E G

) therefore, the position of

G

is independent of the choice of the pair

A

B

Consider now the inversion with respect to the circle of radius

E F

centred at

F

. The inverse of the line

e

is the circle

k

and the inverses of the points

A

and

B

are the points

A'

and

B'

. The inverse of the circle

k_{1}

is the line

A' B'

, and within that, the arc containing

G

is mapped onto the line segment

A' B'

. Thus the line segment

A' B'

is passing through the inverse

G'

of the point

G

, which was shown to be independent of the choice of

A

and

B

□

Remarks. 1. The above solution is based on the properties of inversion, which is not covered by the high school curriculum. The solutions by L. Balogh and P. Maga also use inversion.
2. From the solution above, it is easy to see that if

E F = 1

then

\begin{matrix} F G' = \frac{1}{F G} = \frac{1}{1 + E G} = \frac{1}{1 + A E \cdot E B} . \end{matrix}

The following two solutions are more down to earth.

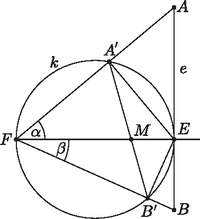
Solution 2. Let

M

denote the intersection of

E F

and

A' B'

. We will show that

M

is the same point for all pairs

A

B

, that is, the length of

F M

is constant. The length of

F M

can be expressed in terms of the ratio of the areas of the triangle

F A' B'

and the quadrilateral

F A' E B'

\begin{matrix} \frac{F M}{E F} = \frac{A_{F A' B'}}{A_{F A' E B'}} . \end{matrix}

Let the length of the line segment

E F

be chosen as unity, and let

∠ A F E = α

and

∠ B F E = β

. Tangency and Thales' theorem imply that the triangles

F E A

F E B

F A' E

and

F B' E

are right-angled, and thus

A E = tan α

B E = tan β

F A' = cos α

F B' = cos β

A' E = sin α

and

B' E = sin β

. Hence the areas in question are

\begin{matrix} A_{F A' B'} & = & \frac{1}{2} F A' \cdot F B' sin (α + β) = \frac{cos α \cdot cos β \cdot sin (α + β)}{2}, \\ A_{F A' E B'} & = & A_{F A' E} + A_{F E B'} = \frac{sin α cos α + sin β cos β}{2} = \frac{sin 2 α + sin 2 β}{4} = \\ = & \frac{sin (α + β) cos (α - β)}{2}, \end{matrix}

and finally,

\begin{matrix} F M & = & \frac{F M}{E F} = \frac{A_{F A' B'}}{A_{F A' E B'}} = \frac{cos α cos β}{cos (α - β)} = \frac{cos α cos β}{cos α cos β - sin α sin β} = \\ = & \frac{1}{1 + tan α tan β} = \frac{1}{1 + E A \cdot E B} . \end{matrix}

Therefore, the length of the line segment

F M

is constant.

□

Solution 3. (Outlines of the solution by G. Kis). Let the centre of

k

be the origin of the cartesian plane and let its radius be equal to unity. Set the coordinates of

A

and

B

(1, a)

and

(1, b)

, respectively. Then the equations of the lines

A F

and

B F

and the circle

k

are

\begin{matrix} \frac{a x}{2} + \frac{a}{2} & = & y \\ \frac{b x}{2} + \frac{b}{2} & = & y \\ x^{2} + y^{2} & = & 1. \end{matrix}

The intersections are obtained by solving the corresponding pairs of simultaneous equations:

\begin{matrix} A' = (\frac{8}{a^{2} + 4} - 1, \frac{4 a}{a^{2} + 4}) and B' = (\frac{8}{b^{2} + 4} - 1, \frac{4 b}{b^{2} + 4}) . \end{matrix}

Hence the equation of the line

A' B'

\begin{matrix} \frac{4 + a b}{2 (a + b)} (x + 1 - \frac{8}{a^{2} + 4}) + \frac{4 a}{a^{2} + 4} = y . \end{matrix}

Substituting

y = 0

, the

x

-coordinate of the intersection of the line

A' B'

with the

x

-axis is

\begin{matrix} x_{0} = \frac{4 + a b}{4 - a b} . \end{matrix}

This quantity is constant since

a b

is constant. Therefore, the lines

A' B'

all pass through the point

(x_{0},0)

□

Problem 2. A

k

-colouring of a graph

G

is a colouring of the points of

G

with

k

available colours, such that the two endpoints of every edge of

G

are coloured differently. A graph

G

is said to have the unique

k

-colouring property if there exists one and only one

k

-colouring of

G

such that there are no points

u

and

v

G

that have the same colour in some

k

-colouring and different colours in another

k

-colouring of

G

.
Prove that if a graph on

n

points has the unique

3

-colouring property and

n \geq 3

then

G

has at least

2 n - 3

edges.

Solution. Consider a fixed 3-colouring of

G

in which there are

n_{1}

n_{2}

n_{3}

vertices, respectively, coloured in the given colours. Then clearly

n_{1} + n_{2} + n_{3} = n

.
Assume that two colour classes (say the red and the green) do not span a connected graph in

G

, that is the subgraph formed by the edges connecting red and green points has at least two components. If the colours are interchanged in one of these components (that is the colour of the green points is changed to red and vice versa), then the edges of the resulting graph still connect points of different colours. Thus we obtain a 3-colouring in which the colour classes form a different partition of the points of

G

. In the new 3-colouring there are either two differently coloured points that previously had the same colour or two similarly coloured points that previously had different colours. This contradicts the unique 3-colouring property of

G

. Therefore, every two colour classes of

G

span a connected graph.
It is known that the number of edges in a connected graph is at most 1 less than the number of its vertices. Hence the number of vertices in the first two colour classes is at least

n_{1} + n_{2} - 1

, the number of vertices in the first and third colour classes is at least

n_{1} + n_{3} - 1

and, finally, the number of vertices in the second and third colour classes is at least

n_{2} + n_{3} - 1

. The edges counted above are clearly different from each other, hence

\begin{matrix} (n_{1} + n_{2} - 1) + (n_{2} + n_{3} - 1) + (n_{3} + n_{1} - 1) = 2 n - 3 \end{matrix}

is indeed a lower bound for the number of edges in

G

□

Remarks. 1. There were several attempts to solve the problem by induction: The statement is clearly true for graphs on 3 points. Assume that the estimation is proved to be correct for graphs on at most

n - 1

points. If the degree of each vertex of a graph on

n

points with a unique 3-colouring is at least 4 then the number of its edges is at least

2 n

and the statement is true. If

G

has a vertex of degree 2 then cancelling that vertex yields a graph with a unique 3-colouring. (This is straightforward.) The resulting graph has at least

2 (n - 1) - 3 = 2 n - 5

edges by assumption, and thus

G

itself has at least

2 n - 5 + 2 = 2 n - 3

edges. We are left to the case when the minimum degree in

G

is 3. Unfortunately, if a vertex of degree 3 happens to be cancelled, then the remaining graph

G - v

will not necessarily have a proper 3-colouring: it may happen that in some 3-colouring of

G - v

the points connected to

v

have different colours. Now if two points of the same colour connected to

v

are glued together, then the resulting graph will have a unique 3-colouring but the number of its edges is only 3 less than the number of edges in

G

. A proof by induction would require a graph that has fewer edges by at least 4.
The Competition Committee does not know of any argument that would improve the above idea to a complete proof by induction.
2. Some competitors showed that the lower bound given in the problem can be attained. It is clear that the complete graph on 3 points has a unique 3-colouring and it has

2 \cdot 3 - 3 = 3

edges. It is also easy to see that adding another vertex to a graph

G

of a unique 3-colouring, connecting it to two differently coloured vertices of

G

yields a new graph with a unique 3-colouring for which the estimation will be sharp if it was sharp for the original graph.
3. With reasonable modifications, the solution can be extended to estimate the number of edges in graphs that have a unique

k

-colouring. It can be shown that a graph with a unique

k

-colouring has at least

\begin{matrix} (k - 1) (n - k) + (\binom{k}{2}) \end{matrix}

edges. Remark 2 can also be generalized: The complete graph on

k

vertices has a unique

k

-colouring, and a vertex added to a graph with a unique

k

-colouring and connected to

k - 1

vertices of different colours will also result a graph with a unique

k

-colouring.
4. Our method also works if instead of the

k

-colouring being unique, we have only an upper bound for the number of

k

-colourings in a graph. The solution provides an upper bound for the component graphs spanned by two colour classes and hence the number of edges spanning two components can be estimated from below.

Problem 3. Let

(a, b)

denote the greatest common factor of the integers

a

and

b

. Prove that apart from a finite number of exceptions,

\begin{matrix} \sum_{i = 1}^{n} \sum_{j = 1}^{n} (i, j) > 4 n^{2} \end{matrix}

for every positive integer

n

Solution 1. Denote the sum on the left-hand side of the above inequality by

f (n)

. Examine how many times a given number

d

occurs as

(i, j)

in the sum. It is clear that if

(i, j) = d

then

\frac{i}{d}

and

\frac{j}{d}

are relative primes and they both lie in the interval

[1, ⌊ \frac{n}{d} ⌋]

where

⌊ n ⌋

denotes the greatest integer not exceeding

n

.
On the other hand, if

i', j' \in [1, ⌊ \frac{n}{d} ⌋]

are relative prime then with

i = i' \cdot d

and

j = j' \cdot d

we have

(i, j) = d

and

i, j \in [1, n]

. This correspondence yields the following rearrangement:

\begin{matrix} f (n) = \sum_{i = 1}^{n} \sum_{j = 1}^{n} (i, j) = \sum_{d = 1}^{n} \sum_{\begin{matrix} (i, j) = d, \\ 1 \leq i \leq n, \\ 1 \leq j \leq n \end{matrix}}^{} d = \sum_{d = 1}^{}^{n} \sum_{\begin{matrix} (i, j) = 1, \\ 1 \leq i \leq \frac{n}{d}, \\ 1 \leq j \leq \frac{n}{d} \end{matrix}}^{} d = \sum_{d = 1}^{n} d \cdot g (\frac{n}{d}), \end{matrix}

(1)

where

g (x)

is the number of coprime pairs formed by the numbers between 1 and

x

. Estimating the value of

g (x)

we will show that

\begin{matrix} g (x) \geq \frac{x^{2}}{100} . \end{matrix}

(2)

Since the pair

(1,1)

is always present (2) is obvious for

x \leq 10

. We shall proceed by subtracting, for each

d

, the number of pairs containing

d

as a common factor from the total number of pairs:

\begin{matrix} g (x) \geq {⌊ x ⌋}^{2} - {⌊ \frac{x}{2} ⌋}^{2} - {⌊ \frac{x}{3} ⌋}^{2} - {⌊ \frac{x}{4} ⌋}^{2} - \dots > {(\frac{9 x}{10})}^{2} - \frac{x^{2}}{2^{2}} - \frac{x^{2}}{3^{2}} - \frac{x^{2}}{4^{2}} - \dots > \\ > & x^{2} (\frac{81}{100} - \frac{1}{4} - (\frac{1}{2 \cdot 3} + \frac{1}{3 \cdot 4} + \frac{1}{4 \cdot 5} \dots)) = \\ = & x^{2} (\frac{81}{100} - \frac{1}{4} - (\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} \dots)) \geq x^{2} (\frac{81}{100} - \frac{1}{4} - \frac{1}{2}) > \frac{x^{2}}{100} . \end{matrix}

Substituting the estimation into (1), we get

\begin{matrix} f (n) = \sum_{d = 1}^{n} d \cdot g (\frac{n}{d}) \geq \sum_{d = 1}^{n} d \cdot \frac{n^{2}}{100 \cdot d^{2}} = \frac{n^{2}}{100} \sum_{d = 1}^{n} \frac{1}{d} . \end{matrix}

(3)

Since the harmonic series diverges,

\sum_{d = 1}^{N} \frac{1}{d} > 400

for some

N

. (For example,

N = 2^{800}

will do.) Applying (3) to

n \geq N

yields

\begin{matrix} \sum_{i = 1}^{n} \sum_{j = 1}^{n} (i, j) = f (n) \geq \frac{n^{2}}{100} \cdot 400 = 4 n^{2} . \end{matrix}

The claim is hence proved.

□

Remarks. 1. It turns out from the proof that the factor 4 on the right-hand side can be replaced by any positive constant. The price for this is that the largest integer for which the inequality of the problem is not true will be greater.
2. Using more sophisticated number-theoretical machinery, it can be shown that the function

g (x)

in the solution approaches

\frac{6}{π^{2}} x^{2}

asymptotically. Hence the sum

f (n)

is equal to

\frac{6}{π^{2}} x^{2} log x

asymptotically.
3. Most solvers found less elementary solutions based on the divergence of the sum of reciprocals of primes. A typical reasoning is outlined below:

Solution 2. The greatest common factor

(i, j)

can be estimated with the sum of the common prime factors of the numbers

i

and

j

. Let

p_{1} < p_{2} < \dots < p_{k}

be the primes dividing both

i

and

j

. Since every prime is at least 2,

\begin{matrix} (i, j) & \geq p_{1} \cdot p_{2} \cdot ... \cdot p_{k} \geq p_{1} + p_{2} \cdot p_{3} \cdot ... \cdot p_{k} \geq & (4) \\ \geq p_{1} + p_{2} + p_{3} \cdot ... \cdot p_{k} \geq \dots \geq p_{1} + p_{2} + \dots + p_{k} . \end{matrix}

It is well known that the sum of the reciprocals of primes tends to infinity. Therefore, there is a number

N

for which the sum of the reciprocals of the primes between 1 and

N

is greater than say 6. Then (4) can be applied to estimate

f (n)

for

n \geq N

as follows:

\begin{matrix} f (n) \geq \sum_{p is prime} \sum_{p ∣ (i, j)} p = \sum_{p is prime} p \cdot {⌊ \frac{n}{p} ⌋}^{2} \geq \sum_{\begin{matrix} p is prime \\ p \leq n \end{matrix}} p {(\frac{n}{p} - 1)}^{2} = \\ = & \sum_{\begin{matrix} p is prime \\ p \leq n \end{matrix}} (\frac{n^{2}}{p} - 2 n + p) > - 2 n^{2} + n^{2} \cdot \sum_{\begin{matrix} p is prime \\ p \leq n \end{matrix}} \frac{1}{p} \geq - 2 n^{2} + n^{2} \cdot \sum_{\begin{matrix} p is prime \\ p \leq N \end{matrix}} \frac{1}{p} \geq \\ \geq & - 2 n^{2} + 6 n^{2} = 4 n^{2} . □ \end{matrix}