Kezdőlap


Cím:	Feuerbach's circle touches the tangent circles
Szerző(k):	Zoltán Füredi
Füzet:	2005/februári melléklet, 7 - 13. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

¹
Two proofs are presented on Feuerbach's theorem seen above.

Notations

The three sides of triangle

A B C

are denoted by

a

b

and

c

the usual way. Let

K

denote the circumscribed circle with centre

O

, and radius

r

;

B

denotes the inscribed circle, its centre is

Q

, its radius is

ϱ

, and the area of the triangle is

t

, its semiperimeter is

s

, its centroid is

S

, its orthocentre is

M

, and the midpoints of the sides are

H_{a}

H_{b}

and

H_{c}

. Heron's formula expresses the area of the triangle in terms of the sides,

\begin{matrix} t = \sqrt[]{s (s - a) (s - b) (s - c)} . \end{matrix}

Further known formulae of area:

\begin{matrix} t = ϱ s = \frac{1}{2} a b sin γ = \frac{a b c}{4 r} . \end{matrix}

From these and the expansion of Heron's formula we get that

\begin{matrix} 2 r ϱ & = \frac{a b c}{a + b + c}, & (1) \\ ϱ^{2} & = \frac{(s - a) (s - b) (s - c)}{s} & (2) \\ = \frac{- a^{3} - b^{3} - c^{3} - 2 a b c + a b^{2} + a c^{2} + b a^{2} + b c^{2} + c a^{2} + c b^{2}}{4 (a + b + c)} . \end{matrix}

Figure 1

Feuerbach's circle

Let

F

denote the circle passing through the midpoints of the sides. Since triangle

H_{a} H_{b} H_{c}

is obtained from triangle

A B C

by a scaling down of centre

S

and factor

- \frac{1}{2}

, the radius of

F

\frac{r}{2}

and its centre is

F

, and it is adjacent to Euler's line of the triangle:

F

is the midpoint of the segment

O M

S

trisects

O M

and

O F

. Euler (1707‐1783) already knew that

F

passes through the feet of the altitudes and the midpoints of segments joining

M

and the vertices. The reason why

F

is still called Feuerbach's circle is the following nice theorem:

Theorem.

F

touches the inscribed and the escribed circles.

In 1822, in his doctoral dissertation Karl Wilhelm Feuerbach (1800‐1834) calculated the distance of the centres of the circles in question. He showed that

| F Q | = | \frac{1}{2} r - ϱ |

. As all data of the triangle can be expressed with

a

b

and

c

, if not in other way, but implicitly, as a root of (simultaneous) equation(s), this calculation can be carried out, at least in principle. If points

A

B

and

C

are placed in a coordinate system as points

(0; 0)

(1; 0)

and

(x; y)

, then only two parameters are needed for the calculations. The calculation may result in higher and higher degree equations, which are more and more difficult to handle. Therefore, the majority of the proofs of the theorem use vectors. The calculation below stands out with its relative shortness. I learnt the most significant elements of the argument (Lemma 1) more than 30 years ago at István Reiman's extracurricular problem-solving course, and it can be found in István Reiman's book titled Geometry and its Frontiers (Gondolat Kiadó, Budapest, 1986).
It is more convenient to determine the square of the distances: avoiding square roots, only rational fractions come in sight. From (1) and (2) it is immediately known how to express the last two terms of

{(\frac{1}{2} r - ϱ)}^{2} = \frac{1}{4} r^{2} - r ϱ + ϱ^{2}

with

a

b

and

c

. For the calculation of

{| F Q |}^{2}

below only

a

b

c

and

r

are used.

Vectors

The task becomes much simpler with the right choice of the origin. In our case let the vector pointing from point

O

X

be denoted by

X

. Then

| A | = | B | = | C | = r

. For any origin

S = \frac{1}{3} (A + B + C)

. As the starting point of the position vectors is

O

and points

O

S

M

and

F

are all adjacent to Euler's line, it follows that

M = 3 S = A + B + C

and

\begin{matrix} F = \frac{1}{2} (A + B + C) . \end{matrix}

(3)

Lemma 1.

\begin{matrix} Q = \frac{a A + b B + c C}{a + b + c} . \end{matrix}

(4)

Proof. Let

P

denote the fraction on the right-hand side of (4). We show that its end-point is lying on the bisectors of the angles, respectively. The length of vector

C - A

b

, thus

\frac{1}{b} (C - A)

is the unit vector from

A

towards

C

. Similarly,

\frac{1}{c} (B - A)

is the unit vector towards

B

. Hence the end-point of the sum of these two, i.e.

\frac{b B + c C - (b + c) A}{b c}

lies on the angle bisector at

A

. Any point of the bisector line can be obtained if the sum is multiplied by a scalar and added to

A

. Removing fractions yields the parametric vector-equation of the angle bisector of

A

\begin{matrix} f_{A} (x) = A + x (b B + c C - (b + c) A) . \end{matrix}

x

runs through real numbers, vectors

f_{A} (x)

yield the points of the angle bisector. Once you know the result, checking is easy: the line defined by

f_{A} (x)

is determined by two of its points:

x = 0

gives vertex

A

x = \frac{1}{b + c}

gives the point of the segment

B C

dividing it in the ratio

c : b

, i.e. the foot of the angle bisector. Choosing

x = \frac{1}{a + b + c}

shows that

P

lies on the bisector indeed. By symmetry,

P

also lies on the other two bisectors, so

P = Q

□

Besides basic properties of vectors (commutativity of addition, linear combination) the notion of scalar product is also needed. As the product of a vector with itself is the square of its length, an arbitrary distance

| X Y |

or its square can be calculated:

{| X Y |}^{2} = {| X - Y |}^{2} = X^{2} + Y^{2} - 2 X Y

. Besides the commutativity and a certain kind of associativity of the dot product, only the values of the products

A B

A C

and

B C

are needed. As

c^{2} = {| B - A |}^{2} = {| B |}^{2} + | A^{2} | - 2 A B = 2 r^{2} - 2 A B

, we get that

\begin{matrix} A B = r^{2} - \frac{1}{2} c^{2}, A C = r^{2} - \frac{1}{2} b^{2}, B C = r^{2} - \frac{1}{2} a^{2} . \end{matrix}

(5)

Proof of the theorem. Calculate the distance of two centres,

F

and

Q

\begin{matrix} Q^{2} = {| Q |}^{2} = {(\frac{a A + b B + c C}{a + b + c})}^{2} & (6) \\ = \frac{a^{2} A^{2} + b^{2} B^{2} + c^{2} C^{2} + 2 a b A B + 2 a c A C + 2 b c B C}{{(a + b + c)}^{2}} \\ = \frac{a^{2} r^{2} + b^{2} r^{2} + c^{2} r^{2} + 2 a b r^{2} - a b c^{2} + 2 a c r^{2} - a c b^{2} + 2 b c r^{2} - b c a^{2}}{{(a + b + c)}^{2}} \\ = r^{2} - \frac{a b c}{a + b + c} . \end{matrix}

From this, (1) yields Euler's theorem:

\begin{matrix} {| Q |}^{2} = r^{2} - 2 r ϱ \end{matrix}

(7)

and hence

\frac{1}{2} r \geq ϱ

\begin{matrix} F^{2} = {| F |}^{2} = \frac{1}{4} {(A + B + C)}^{2} = \frac{1}{4} (3 r^{2} + 2 A B + 2 A C + 2 B C) & (8) \\ = \frac{1}{4} (9 r^{2} - a^{2} - b^{2} - c^{2}), \\ 2 F Q = (A + B + C) \frac{a A + b B + c C}{a + b + c} & (9) \\ = \frac{1}{a + b + c} (a A^{2} + b B^{2} + c C^{2} + (a + b) A B + (a + c) A C + (b + c) B C) \\ = r^{2} + \frac{1}{a + b + c} ((a + b) (r^{2} - \frac{1}{2} c^{2}) + (a + c) (r^{2} - \frac{1}{2} b^{2}) \\ + (b + c) (r^{2} - \frac{1}{2} a^{2})) \\ = 3 r^{2} - \frac{1}{2 (a + b + c)} (a c^{2} + b c^{2} + a b^{2} + c b^{2} + b a^{2} + c a^{2}) . \end{matrix}

Subtract (9) from the sum of equations (6) and (8):

\begin{matrix} {| F - Q |}^{2} = F^{2} + Q^{2} - 2 F Q = \frac{1}{4} r^{2} \\ + \frac{- 4 a b c - (a + b + c) (a^{2} + b^{2} + c^{2}) + 2 (a c^{2} + b c^{2} + a b^{2} + c b^{2} + b a^{2} + c a^{2})}{4 (a + b + c)} \\ = \frac{1}{4} r^{2} - \frac{2 a b c}{4 (a + b + c)} + \frac{- a^{3} - b^{3} - c^{3} - 2 a b c + a b^{2} + a c^{2} + b a^{2} + b c^{2} + c a^{2} + c b^{2}}{4 (a + b + c)} . \end{matrix}

From this, with (1) and (2)

\begin{matrix} {| F - Q |}^{2} = \frac{1}{4} r^{2} - r ϱ + ϱ^{2} = {(\frac{1}{2} r - ϱ)}^{2} . \end{matrix}

The length of segment

F Q

\frac{1}{2} r - ϱ

, and hence the circle of centre

Q

and radius

ϱ

touches the circle of centre

F

and radius

\frac{1}{2} r

(Feuerbach's circle) from inside.

□

Remarks

1. Prove that the vector pointing to the centre of the circle escribed to side

a

\begin{matrix} Q_{a} = \frac{- a A + b B + c C}{- a + b + c} . \end{matrix}

2. Find similar proofs that the inscribed circle touches the escribed ones from outside.

3. According to the theorem of Jean-Victor Poncelet (1788‐1867) if the vertices of

k

-sided polygon

A_{1}, ..., A_{k}

lie on the circle

K

and, at the same time, the sides touch a circle

B

, then starting from an arbitrary point

X = X_{1}

of circle

K

, drawing a tangent line to circle

B

and thus receiving next point

X_{2}

on circle

K

, then carrying on with the procedure, the broken line received after the

k

th step closes, i.e.

X_{k + 1} = X_{1}

.²
Based on Euler's formula (7), prove Poncelet's theorem for

k = 3

4. A theorem similar to Lemma 1 (with an equally simple proof) holds in all dimensions; e.g. if

A_{1}

A_{2}

A_{3}

and

A_{4}

are the vertices of a tetrahedron,

A_{1}

A_{2}

A_{3}

and

A_{4}

are vectors pointing from the centre of the circumscribed sphere to the vertices, and

Q

is the vector pointing to the centre of the inscribed sphere,

Q

, then

\begin{matrix} Q = \sum_{1 \leq i \leq 4}^{} \frac{t_{i}}{t_{1} + \dots + t_{4}} A_{i}, \end{matrix}

where

t_{i}

is the area of the face opposite to

A_{i}

5. Using equation (8) prove that

sin^{2} α + sin^{2} β + sin^{2} γ = 2

if and only if the triangle is right-angled.

6. Prove that Feuerbach's circle

F

touches the inscribed and escribed circles of triangles

A B M

A C M

and

B C M

. (This means 12 further circles!)

Proof by inversion

The simplest proof of Feuerbach's theorem is presented, which has been found by M'Clelland (1891) and Lachlan (1893) independently, and has been adopted by most textbooks (e.g. D. Pedoe: Circles, MAA publication, 1957, 1979, 1995). The proof of the main idea (Lemma 2) below is new and slightly simpler than usual.
Let

A_{0}

denote the point of tangency of the inscribed circle

B

on the side

a

, and

A_{1}

the point of tangency of circle

H

escribed to side

a

, and, finally let

f

be the common axis of symmetry of these two circles, the interior angle bisector at

A

. These two circles have 4 common tangent lines, the sides

ℓ_{a}

ℓ_{b}

ℓ_{c}

, and a fourth line

ℓ_{a}'

, the reflection of

ℓ_{a}

about

f

. Let

B'

and

C'

be the reflections of vertices

B

and

C

about

f

, in this case

B'

C' \in ℓ_{a}'

.
As

| C A_{0} | = s - c

and

| B A_{1} | = s - c

, the midpoint of segment

A_{0} A_{1}

H_{a}

and its length is

| a - 2 (s - c) | = | c - b |

. Suppose that

b \neq c

and let

i

denote the inversion with respect to circle of diameter

A_{0} A_{1}

. In this case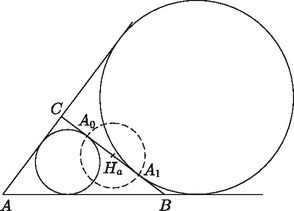

i (A_{0}) = A_{0}

i (A_{1}) = A_{1}

i (ℓ_{a}) = ℓ_{a}

Figure 2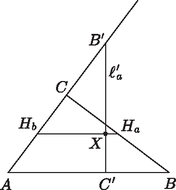

Figure 3

Lemma 2.

i (B) = B

i (H) = H

and

i (ℓ_{a}') = F

Proof. Inversion preserves tangency, thus

i (B)

touches

i (ℓ_{a})

at point

i (A_{0})

. Hence the image of

B

is itself. We get similarly that

i (H) = H

.
It still has to be proved that

i (F) = ℓ_{a}'

. As

F

contains the centre of the inversion,

H_{a}

, its image is a line. We prove that the images of

H_{b}

and

H_{c}

are adjacent to the line

ℓ_{a}'

. Consider

H_{b}

, the case of

H_{c}

is similar. Let

X

be the intersection of lines

H_{a} H_{b}

and

ℓ_{a}'

. The similarity of triangles

B' A C'

and

B' H_{b} X

implies that

\begin{matrix} | H_{b} X | = | A C' | \cdot \frac{| H_{b} B' |}{| A B' |} = | A C' | \cdot \frac{| A B' | - | A H_{b} |}{| A B' |} = b \frac{c - \frac{b}{2}}{c} . \end{matrix}

c - \frac{b}{2}

is negative, then

X

is outside the segment

[H_{b} H_{a}]

. We get that

| H_{b} X | < \frac{c}{2}

and hence,

X

is on the ray

[H_{a} H_{b})

. Moreover,

\begin{matrix} | H_{b} H_{a} | \cdot | X H_{a} | = | H_{b} H_{a} | (| H_{b} H_{a} | - | H_{b} X |) = \frac{c}{2} (\frac{c}{2} - b \frac{c - \frac{b}{2}}{c}) = \frac{1}{4} {(c - b)}^{2} . \end{matrix}

Hence,

i (H_{b}) = X

, so

i (H_{b}) \in ℓ_{a}'

□

Finally, since

ℓ_{a}'

is the common tangent line of

B

and

H

, so

F

is a common tangent (circle) of the images of these two circles. Finally, the same holds for any other escribed circle instead of

H

, the circle

F

touches all four tangent circles, indeed.

Appendix, some properties of inversion

Inversion

i

with respect to a circle of centre

O

and radius

r

is a bijection of the points apart form

O

of the plane so that the image

i (P)

of point

P

is on the ray starting from

O

and passing through

P

such that

| O P | \cdot | O i (P) | = r^{2}

. This is an involution, i.e.

i (i (P)) = P

.
‐ The image of a straight line

ℓ

through

O

is itself (more precisely,

i (ℓ ∖ {O}) = ℓ ∖ {O}

.)
‐ If

O \notin ℓ

, then its image is a circle passing through

O

.
‐ The image of a circle containing

O

is a straight line not containing

O

.
‐ The image of a circle not containing

O

is another circle. Their exterior point of similarity is

O

.
‐ Inversion preserves tangency, and the images of tangent circles and lines also touch each other. Moreover, inversion also preserves angles.

¹Research supported in part by the Hungarian National Science Foundation under grants OTKA T 032452, T 037846 and by the National Science Foundation under grant DMS 0140692.

²More information on Poncelet's theorem can be found in András Hraskó's article in KöMaL 2002/1, pp. 21‐31. (in English).