Cím: Síkidomok felbontása hegyesszögű vagy egyenlő szárú háromszögekre
Szerző(k):  Martin Gardner 
Füzet: 1982/április, 172 - 173. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Síkidomok felbontása hegyesszögű vagy egyenlő szárú háromszögekre
 
(Fordította Fried Ervinné)
 

Egy háromszög hegyesszögű, ha mindegyik belső szöge kisebb 90∘-nál. Mi azon hegyesszögű háromszögek számának minimuma, amennyire egy négyzetet fel lehet bontani úgy, hogy a részek ne fedjék egymást?
Martin Gardner 20 évvel ezelőtt mutatta meg, hogyan lehet egy négyzetet 8 hegyesszögű háromszögre bontani. (1. ábra). A New Mathematical Diversions from Scientific American-ban ezt írta a problémáról: ,,Néhány napig meg voltam győződve, hogy 9 a válasz, amikor hirtelen megláttam, hogyan lehet ezt 8-ra csökkenteni."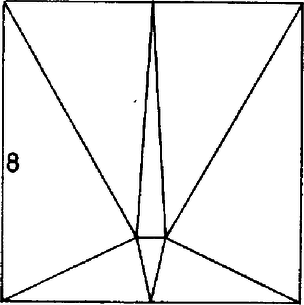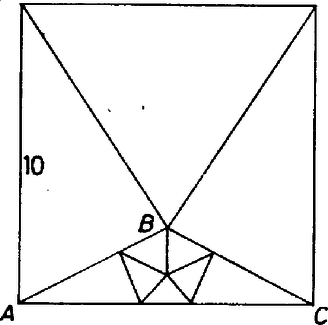
Azóta sok levelet kapott olyan olvasóktól, akiknek nem sikerült 9 hegyesszögű háromszögre bontani a négyzetet, de megmutatták, hogy 10 vagy annál több háromszög esetén lehetséges a megoldás. A 2. ábra 10-re mutat egyet. Megjegyezzük, hogy ebben az ABC tompaszögű háromszög 7 hegyesszögű háromszögre van feldarabolva, továbbá egy ötszög 5 hegyesszögű háromszögre.

Ha mármost az ABC tompaszögű háromszöget felosztjuk egy hegyes- és egy tompaszögű háromszögre a BD szakasszal, ahogyan azt a 3. ábra mutatja, akkor alkalmazni tudjuk az előbbi ötszög-eljárást úgy, hogy a BCD háromszöget osztjuk 7 hegyesszögű háromszögre, és így 11 hegyesszögű háromszöget hozunk létre az eredeti négyzetben. Az eljárást ismételve, előállíthatunk 12. 13 14 hegyesszögű háromszöget.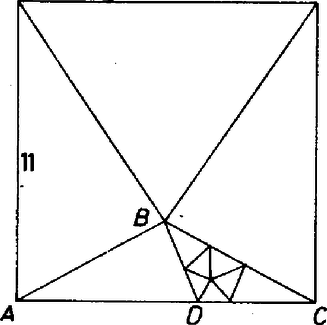

Látszólag 9 hegyesszögű háromszögre a legnehezebb felosztást találni. (4. ábra).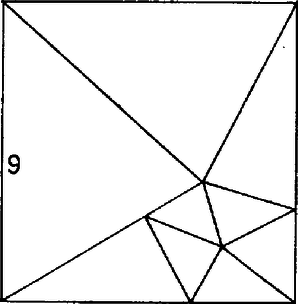

Számos hasonló probléma merült fel más alakzatok (egymást nem fedő) háromszögekkel történő felbontására. Megemlítünk kettőt. Könnyű egy négyzetet felosztani bármilyen 2k számú egyenlő területű háromszögre. Lehet-e azonban felosztani páratlan számú egyenlő területű háromszögre? A meglepő válasz: nem lehet. Tudomásunk szerint az első, aki bizonyította ezt, Paul Monsky volt (American Mathematical Monthly 77. kötet 151-164. old. 1970. febr.)
Egy másik érdekes tétel szerint bármely háromszög felosztható n egyenlő szárú háromszögre, feltéve, hogy n>3. Egy Gali Salvator-tól származó bizonyítás a Crux Mathematicorum-ban 1977-ben jelent meg. Az egyenlő oldalú háromszög esete különösen érdekes. Könnyű felosztani egy egyenlő oldalú háromszöget 4 egybevágó egyenlő szárú háromszögre. (Némely háromszöget nem lehet felosztani 3 vagy 2 egyenlő szárú háromszögre, ezek miatt van szükség a fenti tételben az n>3 feltételre.)
Fel lehet-e osztani egy szabályos háromszöget 5 egyenlő szárú háromszögre? Megmutatjuk, hogy lehet, de nem lesz mind az 5 háromszög szabályos: vagy pontosan 1 vagy pontosan 2 szabályos van közöttük (lásd a borító 4. oldalát). Az nem lehetséges, hogy 2-nél több legyen szabályos.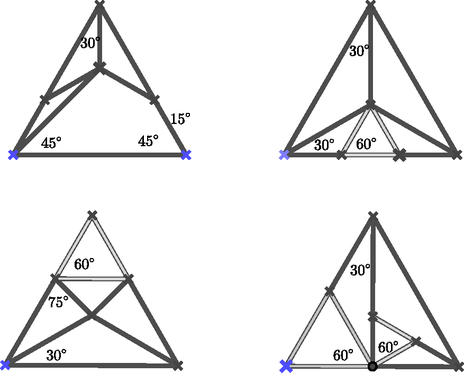