Cím:	Megoldásvázlatok a 2018/4. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Varga Péter
Füzet:	2018/május, 273 - 282. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Egy katonai laktanyában az ábrán látható őrbódéban őrködnek a katonák. A 3,5 m magas építmény egy négyzetes hasábból és egy hozzá kapcsolódó szabályos négyoldalú gúlából áll. Bejárata téglalap alakú, annak felső, rövidebb oldalára illesztett félkörrel. A négyzetes oszlop alapéle 1,3 m, magassága 2,5 m, míg a bejárat téglalap alakú része 0,8 m széles és 1,8 m magas. $a)$ Mennyibe kerül az őrbódé külső lefestése, ha $1\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$ felület lefestéséhez 1,5 dl festék szükséges, melynek literje 3200 Ft? (Az őrbódé tetejét is festjük, ajtaját azonban nem.)  (6 pont) A laktanyában a hétvégi (pénteki, szombati és vasárnapi) éjszakai őrség kialakításakor a parancsnok az alábbi szempontokat veszi figyelembe: $•$ Minden katona legalább egy éjszaka őrködjön, de ne legyen olyan katona, aki mindhárom éjszaka őrségben van. $•$ A teljes létszámnak a fele teljesítsen pontosan két éjszaka őrszolgálatot. $•$ Az őrség létszáma az első éjszaka $16$ fő, a második éjszaka $22$ fő, míg a harmadik éjszaka $10$ fő. $b)$ Hány katona vett részt az éjszakai őrségben?  (5 pont)   Megoldás. $a)$ Az őrbódé külső lefestéséhez szükséges festék mennyiségének meghatározásához számítsuk ki az építmény felszínét. A szabályos négyoldalú gúla oldallapjának $m$ magassága a Pitagorasz-tétellel: $m=\sqrt[]{1^2+0\mathrm{,}{65}^2}=\sqrt[]{1\mathrm{,}4225}$, így a gúla felszíne: $\begin{array}{c}{\displaystyle A_{\text{gúla}}=4\cdot \frac{1\mathrm{,}3\cdot \sqrt[]{1\mathrm{,}4225}}{2}\approx 3\mathrm{,}1\left({\text{m}}^2\right)\mathrm{.}}\end{array}$ A négyzetes hasáb felszíne: $\begin{array}{c}{\displaystyle A_{\text{hasáb}}=4\cdot 1\mathrm{,}3\cdot 2\mathrm{,}5-\left(0\mathrm{,}8\cdot 1\mathrm{,}8+\frac{0\mathrm{,}{4}^2\pi }{2}\right)\approx 11\mathrm{,}3\left({\text{m}}^2\right)\mathrm{.}}\end{array}$ Az őrbódé felszíne a gúla és a hasáb felszínének az összege, vagyis $A_{\text{bódé}}\approx 14\mathrm{,}4\left({\text{m}}^2\right)$. Az őrbódé külső lefestéséhez 3 doboz 1 literes festéket kell megvenni, így a lefestés 9600 Ft-ba kerül. 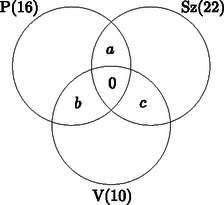$b)$ A feladatban megadott feltételek alapján az alábbi halmazábra készíthető:     Ha $x$ jelöli az éjszakai őrségben résztvevők számát, akkor $a+b+c=\frac{x}{2}$. A három halmaz uniójának elemszámát felírva: $\begin{array}{c}{\displaystyle 16+22+10-\frac{x}{2}-2\cdot 0=x\mathrm{,}\text{így}x=32.}\end{array}$ Tehát 32 katona vett részt az éjszakai őrségben.   2. Egy szabályos dobókockával $20$-szor dobva 5 db egyest, 5 db kettest, 4 db hármast, 3 db négyest és 3 db ötöst dobtunk. $a)$ Számítsuk ki a dobott számok átlagát és szórását.  (3 pont) A dobott számok közül 4 db-ot véletlenszerűen kiválasztunk. $b)$ Hány esetben lesz a kiválasztott számok között legalább egy hármas?  (4 pont) $c)$ Mekkora annak a valószínűsége, hogy mind a négy kiválasztott szám különböző?  (6 pont)   Megoldás. $a)$ A dobott számok átlaga $\frac{54}{20}=2\mathrm{,}7$, szórása $\begin{array}{c}{\displaystyle \sqrt[]{\frac{5\cdot {\left(-1\mathrm{,}7\right)}^2+5\cdot {\left(-0\mathrm{,}7\right)}^2+4\cdot {\mathrm{0,3}}^2+3\cdot \mathrm{1,}{3}^2+3\cdot 2\mathrm{,}{3}^2}{20}}=\sqrt[]{1\mathrm{,}91}\approx 1\mathrm{,}38.}\end{array}$ $b)$ Az összes eset számából levonjuk a kedvezőtlen esetek számát. A 20 dobott számból 4-et minden lehetséges módon $\left(\genfrac{}{}{0ex}{}{20}{4}\right)=4845$-féleképpen választhatunk ki, ez az összes eset száma. Kedvezőtlen esetek azok, amelyekben a kiválasztott számok között nincs hármas, melyek száma $\left(\genfrac{}{}{0ex}{}{16}{4}\right)=1820$. Összesen tehát $4845-1820=3025$ esetben lesz a kiválasztott számok között legalább egy hármas. $c)$ A 20 dobott számból 4-et minden lehetséges módon $\left(\genfrac{}{}{0ex}{}{20}{4}\right)=4845$-féleképpen választhatunk ki, ez az összes eset száma. Ha a kiválasztásnál az 1-esből vagy a 2-esből nem választunk, de a többiből egyet-egyet igen, akkor a kedvező esetek száma: $\left(\genfrac{}{}{0ex}{}{5}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot {\left(\genfrac{}{}{0ex}{}{3}{1}\right)}^2=180$. Ha a kiválasztásnál a 3-asból nem választunk, de a többiből egyet-egyet igen, akkor a kedvező esetek száma: ${\left(\genfrac{}{}{0ex}{}{5}{1}\right)}^2\cdot {\left(\genfrac{}{}{0ex}{}{3}{1}\right)}^2=225$. Ha a kiválasztásnál a 4-esből vagy az 5-ösből nem választunk, de a többiből egyet-egyet igen, akkor a kedvező esetek száma: ${\left(\genfrac{}{}{0ex}{}{5}{1}\right)}^2\cdot \left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{1}\right)=300$. A keresett valószínűség (a kedvező esetek számának és az összes eset számának hányadosa): $\begin{array}{c}{\displaystyle p=\frac{2\cdot \left(\genfrac{}{}{0ex}{}{5}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot {\left(\genfrac{}{}{0ex}{}{3}{1}\right)}^2+{\left(\genfrac{}{}{0ex}{}{5}{1}\right)}^2\cdot {\left(\genfrac{}{}{0ex}{}{3}{1}\right)}^2+2\cdot {\left(\genfrac{}{}{0ex}{}{5}{1}\right)}^2\cdot \left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{3}{1}\right)}{\left(\genfrac{}{}{0ex}{}{20}{4}\right)}=\frac{79}{323}\approx 0\mathrm{,}2446.}\end{array}$   3. $a)$ Az $\text{u}\left(1;\text{log}{}_{8}x\right)$ és $\text{v}\left(\text{log}{}_{2}x;-1\right)$ vektorok merőlegesek egymásra. Határozzuk meg $x$ értékét $\left(x>0\right)$.  (5 pont) $b)$ Adott a síkon $n$ db pont, melyek közül semelyik három nem illeszkedik egy egyenesre $\left(n\ge 3\right)$. Határozzuk meg $n$ értékét, ha a pontok $20$-szor annyi négyszöget határoznak meg, mint egyenest.  (8 pont)   Megoldás. $a)$ I. megoldás. Ha két vektor merőleges egymásra, akkor a skaláris szorzatuk nulla. A skaláris szorzatot a koordináták segítségével felírva megoldandó az alábbi egyenlet: $\text{log}{}_{2}x-\text{log}{}_{8}x=0$. A 8-as alapú logaritmust átírva: $\text{log}{}_{8}x=\frac{\text{log}{}_{2}x}{\text{log}{}_{2}8}$, mellyel a megoldandó egyenlet $\text{log}{}_{2}x=0$, ahonnan $x=1$, mely megoldása a feladatnak. II. megoldás. A $\text{v}$ vektor akkor merőleges az $\text{u}$ vektorra, ha $\text{v}$ koordinátáit felcserélve, és egyiknek az előjelét megváltoztatva éppen $\text{u}$ koordinátáit kapjuk. Az előbbiek miatt megoldandó az alábbi egyenlet: $\text{log}{}_{8}x=\text{log}{}_{2}x$. A 8-as alapú logaritmust átírva: $\text{log}{}_{8}x=\frac{\text{log}{}_{2}x}{\text{log}{}_{2}8}$, mellyel a megoldandó egyenlet $\text{log}{}_{2}x=0$, ahonnan $x=1$, mely megoldása a feladatnak. $b)$ $n$ db a feltételeknek megfelelő pont $\left(\genfrac{}{}{0ex}{}{n}{4}\right)$ db pontnégyest, és $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ db egyenest határoz meg, tehát megoldandó az $\left(\genfrac{}{}{0ex}{}{n}{4}\right)=20\cdot \left(\genfrac{}{}{0ex}{}{n}{2}\right)$ egyenlet. Az előbbi egyenlet az alábbi alakban írható: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)\left(n-2\right)\left(n-3\right)}{4\cdot 3\cdot 2\cdot 1}=20\cdot \frac{n\left(n-1\right)}{2\cdot 1}\mathrm{.}}\end{array}$ Az $\frac{n\cdot \left(n-1\right)}{2}\ne 0$ kifejezéssel osztva az egyenlet mindkét oldalát: $\frac{\left(n-2\right)\cdot \left(n-3\right)}{4\cdot 3}=20$, melyből az $n^2-5n-234=0$ másodfokú egyenletet kapjuk. Az egyenlet pozitív gyöke 18 (negatív gyöke $-13$), tehát a pontok száma 18. Ellenőrzés: a 18 pont 3060 db négyszöget, illetve 153 db egyenest határoz meg, és $20\cdot 153=3060$.   4. Adott az $f:\text{R}\to \text{R}$, $x\mapsto x^4+3x^2+1$ függvény. $a)$ Igazoljuk, hogy az $f$ függvény szigorúan monoton csökken a negatív valós számok halmazán.  (3 pont) $b)$ Igazoljuk, hogy az $f$ függvény páros.  (4 pont) $c)$ Adjuk meg az $f$ függvénynek azt az $F$ primitív függvényét, amelyre $F\left(-1\right)=2$.  (4 pont) $d)$ Állapítsuk meg a $\underset{x\to \infty }{\overset{}{\underset{}{\overset{}{\text{lim}}}}}\frac{3x^2+1}{x^4}$ határértéket.  (3 pont)   Megoldás. $a)$ Az $f$ függvény differenciálható az értelmezési tartományán és $f\text{'}\left(x\right)=4x^3+6x$. Ha $x<0$, akkor $4x^3<0$ és $6x<0$, így $f\text{'}\left(x\right)<0$. Ha $x<0$ és $f\text{'}\left(x\right)<0$, akkor az $f$ függvény szigorúan monoton csökken a negatív valós számok halmazán. $b)$ Az $f$ függvény páros, ha az értelmezési tartomány bármely $x_0$ eleme esetén $-x_0$ is eleme az értelmezési tartománynak és bármely $x_0$-ra $f\left(x_0\right)=f\left(-x_0\right)$. Az $f$ függvény értelmezési tartománya a valós számok halmaza, ezért bármely $x_0$ esetén annak ellentettje is eleme az értelmezési tartománynak. $\begin{array}{c}{\displaystyle f\left(x_0\right)=x_0^4+3x_0^2+\mathrm{1,}f\left(-x_0\right)={\left(-x_0\right)}^4+3{\left(-x_0\right)}^2+1.}\end{array}$ Mivel egy valós számnak és ellentettjének negyedik hatványa, valamint négyzete megegyezik, ezért $f\left(x_0\right)=f\left(-x_0\right)$, tehát az $f$ függvény páros. $c)$ $\begin{array}{c}{\displaystyle \int \left(x^4+3x^2+1\right)\text{d}x=\frac{x^5}{5}+x^3+x+C\mathrm{.}}\end{array}$ Mivel $F\left(-1\right)=2$, így $\frac{{\left(-1\right)}^5}{5}+{\left(-1\right)}^3+\left(-1\right)+C=2$, ahonnan $C=\frac{21}{5}$. A keresett függvény: $\begin{array}{c}{\displaystyle F\left(x\right)=\frac{x^5}{5}+x^3+x+\frac{21}{5}\mathrm{.}}\end{array}$ $d)$ $\begin{array}{c}{\displaystyle \underset{x\to \infty }{\overset{}{\text{lim}}}\frac{3x^2+1}{x^4}=\underset{x\to \infty }{\overset{}{\text{lim}}}\frac{\frac{3}{x^2}+\frac{1}{x^4}}{1}\mathrm{.}}\end{array}$ Mivel $x\to \infty$, így az előbbi tört számlálója 0-hoz, nevezője 1-hez tart, ezért a keresett határérték 0.   II. rész     5. $a)$ A tízes számrendszerben felírt $\overline{abc}$ háromjegyű szám számjegyei a felírás sorrendjében egy számtani sorozat egymást követő három elemét alkotják. Ha a háromjegyű számot elosztjuk a számjegyeinek összegével, $26$-ot kapunk. Ha az eredeti számban a százasok és az egyesek számát felcseréljük, az eredetinél $396$-tal nagyobb számot kapunk. Melyik ez a háromjegyű szám?  (7 pont) $b)$ Adjuk meg azokat a különböző számjegyekből álló tízes számrendszerben felírt $\overline{a6c}$ alakú háromjegyű számokat, amelyek a $4$, $6$ és $9$ számok közül pontosan kettővel oszthatók.  (7 pont) $c)$ Lehet-e $a^p\cdot b^q\cdot c^r$ négyzetszám, ha $a$, $b$ és $c$ különböző prímszámok, $p$, $q$ és $r$ pedig különböző páratlan egészek?  (2 pont)   Megoldás. $a)$ Jelöljük az eredeti számban a tízesek helyén álló számjegyet $b$-vel, ekkor a feladatban megfogalmazott feltétel alapján a százasok helyén $b-d$, az egyesek helyén $b+d$ áll, ahol $d$ a számtani sorozat differenciája. Az előbbiek felhasználásával az eredeti háromjegyű szám: $100\left(b-d\right)+10b+b+d=111b-99d$. Ha az eredeti számot elosztjuk a számjegyeinek összegével, akkor $\frac{111b-99d}{3b}=26$, ahonnan $b=3d$. Ha az eredeti szám számjegyeit felcseréljük, akkor a felcserélt szám: $100\left(b+d\right)+10b+b-d=111b+99d$ lesz. A feladat szövege alapján az alábbi egyenlet írható fel: $111b-99d=111b+99d-396$, ahonnan $d=2$. A keresett szám a 468. Ellenőrzés: a 468 háromjegyű szám számjegyei a felírás sorrendjében valóban egy számtani sorozat három egymást követő elemét alkotják, és $\frac{468}{4+6+8}=26$, továbbá $864-468=396$. $b)$ Egy háromjegyű szám a 4, 6 és 9 számok közül pontosan kettővel osztható, ha ${\displaystyle \begin{array}{cc}{\displaystyle \text{<span style="font-style: italic;">I. eset:</span>}}\hfill & {\displaystyle \text{osztható 4-gyel és 9-cel, de nem osztható 6-tal;}}\hfill \\ {\displaystyle \text{<span style="font-style: italic;">II. eset:</span>}}\hfill & {\displaystyle \text{osztható 4-gyel és 6-tal, de nem osztható 9-cel;}}\hfill \\ {\displaystyle \text{<span style="font-style: italic;">III. eset:</span>}}\hfill & {\displaystyle \text{osztható 6-tal és 9-cel, de nem osztható 4-gyel. }}\hfill \end{array}}$ I. eset: Ha $4\mid \overline{a6c}$ és $9\mid \overline{a6c}$, akkor $2\mid \overline{a6c}$ és $3\mid \overline{a6c}$, amiből következik, hogy $6\mid \overline{a6c}$, tehát ilyen eset nem lehetséges. II. eset: Ha $4\mid \overline{a6c}$ és $6\mid \overline{a6c}$, akkor $\overline{6c}$-nek 4-gyel oszthatónak kell lennie, továbbá teljesülnie kell annak is, hogy $3\mid a+6+c$, de 9-cel ne legyen osztható $a+6+c$. Az előbbi feltételek csak akkor teljesülnek ($a\ne c$-t is figyelembevéve), ha $\left(a;c\right)=\left(9;0\right)$, $\left(2;4\right)$, $\left(5;4\right)$, $\left(1;8\right)$ vagy $\left(7;8\right)$. III. eset: Ha $6\mid \overline{a6c}$ és $9\mid \overline{a6c}$, akkor a 2-vel való oszthatóság miatt $c$-nek párosnak kell lennie, továbbá $9\mid a+6+c$, de $\overline{6c}$ nem lehet 4-gyel osztható. Az előbbi feltételek $a\ne c$ esetén pontosan akkor teljesülnek, ha $\left(a;c\right)=\left(1;2\right)$. Az összes megfelelő háromjegyű szám: 162; 168; 264; 564, 768, 960. $c)$ Mivel egy négyzetszám prímtényezős felbontásában minden prím kitevője páros, ezért $a^p\cdot b^q\cdot c^r$ nem lehet négyzetszám.   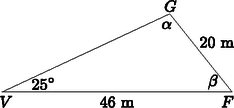6. Egy földmérő noteszában egy vízszintes háromszög alakú telekről a következő bejegyzés olvasható: ,,A telek három sarkán villanypózna, fúrt kút és gázcsonk található. A villanypózna a fúrt kúttól 46 méterre, a fúrt kút a gázcsonktól 20 méterre található. A villanypóznánál állva a fúrt kút és a gázcsonk alkotta szakasz 25$°$-os szögben látszik.'' $a)$ Számítsuk ki a háromszög alakú telek lehetséges területét.  (5 pont) Az előbbi telken a víz-, a gáz- és az elektromos ellátottság nagyon fontos, ugyanis azon kereskedelmi egység épül. Az elektromos rendszer költsége a víz- és a gázellátás költségeinek mértani közepe. Ha a gázellátás költségeit 100 000 Ft-tal csökkentenénk, akkor a víz-, az elektromos- és a gázellátás költségei ebben a sorrendben számtani sorozatot alkotnának. Az elektromos költségek a vízellátás költségeinek $150\%$-át teszik ki. $b)$ Mennyibe kerülnek a felsorolt közművek egyenként?  (6 pont) A telken a víz-, gáz- és az elektromos ellátottság kivitelezésére hat árajánlat érkezett hat különböző vállalkozástól. $c)$ Igazoljuk, hogy a versenytárgyalás résztvevői között biztosan van három olyan személy, akik kölcsönösen ismerik, vagy három olyan, akik kölcsönösen nem ismerik egymást (Egy vállalkozást egy tárgyalópartner képvisel).  (5 pont)   Megoldás. $a)$ Jelölje a háromszög alakú telek egyik sarkában lévő villanypóznát $V$, a másikban lévő fúrt kutat $F$, míg a harmadik csúcsban lévő gázcsonkot $G$.     A $VFG$ háromszögben a szinusztételt alkalmazva: $\frac{\text{sin}\alpha }{\text{sin}{25}^{\circ }}=\frac{46}{20}$, ahonnan ${\alpha }_1\approx 76\mathrm{,}{41}^{\circ }$ vagy ${\alpha }_2\approx 103\mathrm{,}{59}^{\circ }$. Az előbbi szögek ismeretében a megfelelő $\alpha$ szögekhez tartozó $\beta$ szögek a háromszög belső szögeinek összege alapján: ${\beta }_1\approx 78\mathrm{,}{59}^{\circ }$ vagy ${\beta }_2\approx 51\mathrm{,}{41}^{\circ }$. A háromszög alakú telek lehetséges területe a trigonometrikus területképlet alapján: $\begin{array}{c}{\displaystyle T_{VFG}=\frac{46\cdot 20\cdot \text{sin}{\beta }_1}{2}\approx 451{\text{m}}^2\text{vagy}{T}_{VFG\text{'}}=\frac{46\cdot 20\cdot \text{sin}{\beta }_2}{2}\approx 360{\text{m}}^2\mathrm{.}}\end{array}$ $b)$ Jelölje a vízellátás költségét $V$, a gázellátásét $G$, míg az elektromos rendszerét $E$. A feladat szövege alapján $E=\sqrt[]{V\cdot G}$ és $E=1\mathrm{,}5\cdot V$. Mivel a számtani sorozat $n$-edik ($n>1$) eleme a tőle szimmetrikusan elhelyezkedő elemek számtani közepe, ezért a következő egyenlet írható fel: $\begin{array}{c}{\displaystyle V+2\mathrm{,}25\cdot V-100000=3\cdot V\mathrm{,}\text{ahonnan}V=400000\text{Ft}\mathrm{.}}\end{array}$ A vízellátás költségeinek ismeretében $E=600000$ Ft, valamint $G=900000$ Ft. $c)$ A versenytárgyalás minden résztvevőjének legfeljebb 5 ismerőse lehet a tárgyalás résztvevői között. Válasszunk ki egy résztvevőt a tárgyalók közül, legyen ő $A$. A skatulyaelv alapján két eset lehetséges: I. eset: $A$ legalább 3 másik résztvevőt ismer (például $B$-t, $C$-t és $D$-t). Ha $B$, $C$ és $D$ között van kettő, akik ismerik egymást, például $B$ és $C$, akkor találtunk három olyan résztvevőt, akik kölcsönösen ismerik egymást ($A$, $B$, $C)$. Ha $B$, $C$ és $D$ között nincs kettő, akik ismernék egymást, akkor ők kölcsönösen nem ismerik egymást. II. eset: $A$ legalább 3 másik résztvevőt nem ismer (például $B$-t, $C$-t és $D$-t). Az I. esethez hasonló okoskodással: Ha $B$, $C$ és $D$ között van kettő, akik nem ismerik egymást, például $B$ és $C$, akkor találtunk három olyan résztvevőt, akik kölcsönösen nem ismerik egymást ($A$, $B$, $C)$. Ha $B$, $C$ és $D$ között nincs kettő, akik nem ismernék egymást, akkor ők kölcsönösen ismerik egymást. Tehát az előbbiek miatt mindig van három olyan résztvevő, akik kölcsönösen ismerik, vagy kölcsönösen nem ismerik egymást.   7. Tekintsük a következő, fagráfra vonatkozó állítást: Ha 5 fagráfnak összesen 41 éle van, és ezeket a fagráfokat egy gráfnak tekintjük, akkor ezen gráf pontjainak száma páros. $a)$ Adjuk meg az előbbi állítás logikai értékét (igaz vagy hamis). A választ indokoljuk.  (3 pont) $b)$ Igazoljuk, hogy ha egy ötpontú egyszerű gráfnak $8$ éle van, akkor a gráfnak van legalább két olyan pontja, amelyből pontosan három él indul ki.  (5 pont) 2017. november 8-án a Fővárosi Állat- és Növénykertben kiselefánt született. A hírt először csak az állat egyik gondozója tudja. $c)$ Hányféleképpen juthat el a hír a többi 4 gondozóhoz, ha mindenki telefonon beszél a másikkal, és a lehető legkevesebb hívással értesül mindenki a hírről?  (8 pont)   Megoldás. $a)$ Mivel egy $n$ pontú fagráf éleinek száma $n-1$, így az 5 db fagráfnak 5-tel kevesebb éle van, mint pontja. Az előbbiek miatt az 5 db különböző, diszjunkt fagráfból álló gráf csúcsainak száma 46, tehát az állítás igaz. $b)$ Tekintsünk egy 5 pontú teljes gráfot, vagyis egy olyan gráfot, amelyben minden pontot minden másikkal pontosan egy él köt össze. Az előbbi gráfnak összesen 10 éle van. Töröljünk le a 10 élből kettőt, hogy 8 élünk legyen. Elsőként bármelyik élet letörölhetjük, ekkor olyan gráfot kapunk, amelyben két pontból 3, a többi háromból 4 él indul ki. Másodikként vagy olyan élet törlünk le, amely az egyik 3 és az egyik 4 fokszámú pontot köti össze, vagy olyat, amely két 4 fokszámú pontot köt össze. Utóbbi esetben négy 3- és egy 4 fokszámú pont marad, míg előbbi esetben egy 2-, két 3- és két 4 fokszámú pont marad. Látható, hogy mindegyik esetben van legalább két 3 fokszámú pont. $c)$ Jelölje $A$ azt a gondozót, aki először tudja meg a hírt. Összesen 4 telefonhívás kell ahhoz, hogy mindenkihez eljusson a hír. Ha $A$ hívja fel mind a 4 másik gondozót, akkor 1 eset van. Ha $A$ csak 3 másik gondozót hív fel, és a 3 felhívott gondozó közül valamelyik hívja fel a negyediket, akkor összesen $4\cdot 3=12$ eset van. Ha $A$ csak 2 másik gondozót hív fel, akkor a 2 felhívott gondozót $\left(\genfrac{}{}{0ex}{}{4}{2}\right)$-féleképpen választhatja ki. $A$ bármely 2 gondozót hívja fel, a másik 2 gondozó 8-féleképpen értesülhet a hírről, így összesen $\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 8=48$ ilyen eset van. Ha $A$ csak 1 másik gondozót hív fel, akkor a 4 gondozó közül bármelyiket felhívhatja. Bármelyiküket hívja fel, a felhívott felhívhatja mind a 3 másik gondozót, ami 1 eset. Az $A$ által felhívott gondozó felhívhat 2 gondozót, és utána valamelyikük hívja fel a negyedik gondozót, aki még nem értesült a hírről. Ezt 6-féleképpen tehetik meg. Az $A$ által felhívott gondozó 1 gondozót hív fel, és ő hívja fel a többieket, ez 3 eset. Mindenki 1 gondozót hív fel, ami $3\cdot 2\cdot 1=6$ eset. Mivel $A$ négyféleképpen választhatja ki, hogy melyik gondozót hívja fel, ezért itt összesen $4\cdot \left(1+6+3+6\right)=64$ eset van. Az 5 gondozó összesen 125-féleképpen értesítheti egymást.   8. Az ábrán egy 300 méter hosszú egyenes alagút bejárata látható, mely egy 8 méter sugarú kör egy része. Az alagúton keresztülvivő autóút az alagút tetejétől 9,5 méterre található.     $a)$ Milyen széles az autóút?  (3 pont) $b)$ Mekkora térfogatú kőzetmennyiséget kellett eltávolítani az alagút fúrása során?  (5 pont) Egy túlméretes szállítmány olyan téglatest alakú tárgyat szállít, melyet a jármű 1,5 méter magasan lévő platójára helyeznek. $c)$ Mekkora lehet legfeljebb egy olyan tárgy keresztmetszete, ami még átvihető a kétsávos alagúton szabályosan közlekedve?  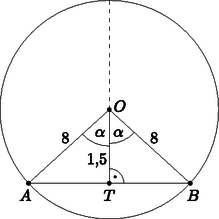(8 pont)   Megoldás. $a)$ Az ábra szerint az $OTB$ derékszögű háromszögben az $TB$ szakasz hossza (m-ben számolva) $TB=\sqrt[]{8^2-1\mathrm{,}{5}^2}=\sqrt[]{61\mathrm{,}75}$ (m), így az autóút kb. 15,7 m széles.     $b)$ Az ábra szerint az $OTB$ derékszögű háromszögből: $\text{cos}\alpha =\frac{1\mathrm{,}5}{8}=0\mathrm{,}1875$, ahonnan $\alpha \approx 79\mathrm{,}{2}^{\circ }$, tehát a nagyobbik körcikk középponti szöge ${360}^{\circ }-2\alpha \approx 201\mathrm{,}{6}^{\circ }$. Az $AOB$ egyenlő szárú háromszög területe: $\begin{array}{c}{\displaystyle T_1=\frac{8^2\cdot \text{sin}2\alpha }{2}\left(\approx 11\mathrm{,}8{\text{m}}^2\right)\mathrm{.}}\end{array}$ A teljes kör területe $T=8^2\pi \left(\approx 201\mathrm{,}1{\text{m}}^2\right)$, ezért a nagyobb körcikk területe $\begin{array}{c}{\displaystyle T_2=\frac{{360}^{\circ }-2\alpha }{{360}^{\circ }}\cdot 8^2\pi \left(\approx 112\mathrm{,}6{\text{m}}^2\right)\mathrm{,}}\end{array}$ a nagyobb körszelet területe $T_1+T_2\approx 124\mathrm{,}4{\text{m}}^2$. Az eltávolított kőzetmennyiség kb. $300\cdot \mathrm{124,4}=37320$ m${}^3$. 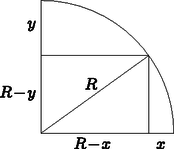$c)$ Az ábra jelöléseit használva írjuk fel a téglalap alakú síkmetszet területét: $T=\left(R-x\right)\left(R-y\right)$, ugyanakkor ${\left(R-x\right)}^2+{\left(R-y\right)}^2=R^2$.     Az $\frac{a^2+b^2}{2}\ge ab$ egyenlőtlenség alapján $a=R-x$ és $b=R-y$ választással $\frac{R^2}{2}\ge T$ adódik. Egyenlőség csak $a=b$, vagyis $x=y$ esetén lesz, amikor is $\begin{array}{c}{\displaystyle R-x=R-y=\frac{R\cdot \sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Tehát a maximálisan átvihető tárgy keresztmetszete egy négyzet, melynek oldala kb. $\left(4\sqrt[]{2}\approx \right)5\mathrm{,}7$ méter.   9. A gumiszerelő műhelyben a szakember tudja, hogy normál körülmények között a gépjárművek első ‐ meghajtott ‐ két kerekén lévő gumik $30000$ kilométer alatt, a hátsó gumik $50000$ kilométer alatt kopnak el. $a)$ Hány kilométert képes biztonságosan autózni adott gumiszettel az autós, ha az első- és hátsó tengelyen lévő kerekek egymással kicserélhetők?  (6 pont) A személygépkocsikra való gumik gyártósoráról lekerülő termékeket nagyon alaposan ellenőrzik. Egy gyártósori széria jellemzően $80000$ gumit tartalmaz, melyből általában $400$ darab hibás (méret és/vagy anyag összetételi eltérés miatt). Az automatikus minőségellenőrzésen az ellenőrző berendezés csak a valóban hibás gumik $99\%$-át találja meg, a jó termékek $2\%$-át viszont hibásnak minősíti. $b)$ Mekkora annak a valószínűsége, hogy az automatikus ellenőrző berendezés által hibásnak minősített gumi valóban hibás?  (5 pont) $c)$ Mekkora valószínűséggel képes az automatikus ellenőrző berendezés a jó minősítést megállapítani?  (5 pont)   Megoldás. $a)$ Ha az első tengelyen 30 000 km, a hátsón 50 000 km megtétele után kopik el a meghajtott gumi, akkor az első tengelyen a gumi $\frac{1}{30000}$-ed, a hátsó tengelyen pedig $\frac{1}{50000}$-ed része kopik el kilométerenként. Jelölje $a$ az első, míg $b$ a hátsó tengelyen futott km-ek számát, ekkor mindkét gumipárra felírható az alábbi egyenlet: $\frac{a}{30000}+\frac{b}{50000}=1$, amiből $5a+3b=150000$. Mivel az előbbi egyenlet mindkét gumipárra igaz és az egyenletes kopás miatt $a=b$, ezért $8a=150000$, ahonnan $a=18750$ km. Tehát mindkét tengelyen 18 750 km-t fut a gumipár, így összesen maximum 37 500 km-t lehet velük biztonságosan megtenni. $b)$ és $c)$   ${\displaystyle \begin{array}{|cccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{ Jó gumi}}\hfill & \hfill {\displaystyle \text{Hibás gumi}}\hfill & \hfill {\displaystyle \text{Összesen }}\hfill \\ {\displaystyle \text{Jónak minősíti}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>995</mn><mo>⋅</mo><mn>0</mn><mn>,</mn><mn>98</mn><mo stretchy="false">=</mo><mn>0</mn><mn>,</mn><mn>9751</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>005</mn><mo>⋅</mo><mn>0</mn><mn>,</mn><mn>01</mn><mo stretchy="false">=</mo><mn>0</mn><mn>,</mn><mn>00005</mn></math>}}\hfill & \hfill {\displaystyle \text{ 0,97515 }}\hfill \\ {\displaystyle \text{Hibásnak minősíti}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>995</mn><mo>⋅</mo><mn>0</mn><mn>,</mn><mn>02</mn><mo stretchy="false">=</mo><mn>0</mn><mn>,</mn><mn>0199</mn></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>0</mn><mn>,</mn><mn>005</mn><mo>⋅</mo><mn>0</mn><mn>,</mn><mn>99</mn><mo stretchy="false">=</mo><mn>0</mn><mn>,</mn><mn>00495</mn></math>}}\hfill & \hfill {\displaystyle \text{ 0,02485 }}\hfill \\ {\displaystyle \text{Összesen}}\hfill & \hfill {\displaystyle \text{ 0,995}}\hfill & \hfill {\displaystyle \text{ 0,005}}\hfill & \hfill {\displaystyle \text{1 }}\hfill \\ \hline\end{array}}$   A táblázat alapján annak a valószínűsége, hogy az automatikus ellenőrző berendezés által hibásnak minősített gumi valóban hibás: $\begin{array}{c}{\displaystyle p=\frac{0\mathrm{,}00495}{0\mathrm{,}00495+0\mathrm{,}0199}=\frac{99}{497}\approx 0\mathrm{,}1992.}\end{array}$ A táblázat alapján annak a valószínűsége, hogy az automatikus ellenőrző berendezés a megfelelő minősítést állapítja meg: $p=0\mathrm{,}9751+0\mathrm{,}00495=0\mathrm{,}98005$.