Cím:	Taxik és távolságok
Szerző(k):	Horváth Manuéla
Füzet:	2018/május, 258 - 271. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. A taxi geometria bevezetése Az euklideszi geometriában két pont távolságát ,,légvonalban'' határozzuk meg (lásd az 1. ábrát). Ezzel szemben a taxi geometria esetében, mint ahogy azt az elnevezése is sugallja, a $P$ és $Q$ pontok közötti távolságot úgy adjuk meg, ahogy egy taxi haladna a legrövidebb úton egy városban $P$ pontból $Q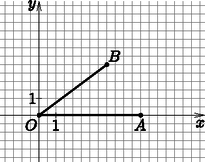$-ba.   1. ábra   A taxi geometria egy jobb modellt ad a városi közlekedésre, mint az euklideszi. Az ebben a geometriában mért távolság sokkal hasznosabb információ lehet a közlekedő ember számára, mint az euklideszi, mivel sajnos rá vagyunk kényszerülve, hogy utcákon, járdákon közlekedjünk, és nincs alkalmunk légvonalban eljutni valahova. Az, hogy egy pont tőlünk az euklideszi távolság szerint pontosan $\sqrt[]{30}$ egységnyi távolságra van, általában nem túl hasznos információ. Az emberek számára tehát gyakran az igazi távolság a taxi távolság. De ‐ ahogy minden alkalommal, mikor matematikai modellt készítünk egy valós rendszerre ‐ szükség van bizonyos egyszerűsítő feltételekre, mivel nélkülük a modell felállítása vagy a probléma megoldása túl bonyolulttá válhat. Esetünkben jelentősen leegyszerűsítjük a város képét: minden utcának észak-dél, illetve kelet-nyugat irányúnak kell lennie, mint ahogyan ezt a 2. ábra is szemlélteti, az utcáknak nincsen szélessége, az utcák kereszteződései az egész koordinátájú pontok, és egy háztömböt egy négyzetrács jelöl. Sajnos nincs olyan település a világon, amely teljesen megfelelne ezeknek a feltételeknek, léteznek viszont városrészek, amelyek nagyjából igen. Ilyenek például az amerikai egyesült államokbeli New Yorkban található Manhattan egyes részei. 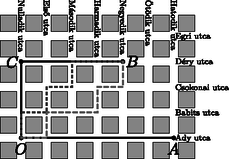  2. ábra   Most pedig képzeljük el az $A$ és $B$ pontokat, mintha egy város különböző pontjai lennének a 2. ábrához hasonlóan. Ekkor már teljesen máshogy gondolkodunk, ha azt szeretnénk megtudni, hogy a kiindulási helyünktől, vagyis az $O$ ponttól, az Ady és a Hatodik utca kereszteződésében lévő $A$ pont, vagy a Déry és a Negyedik utca találkozásánál található $B$ pont van közelebb. Elsődlegesen nem a Pitagorasz-tétellel fogunk okoskodni, hanem egyszerűen megszámoljuk, hogy hány háztömbnyi távolságot kell megtennünk úgy, hogy csak a tengelyekkel párhuzamosan haladhatunk, hogy eljussunk a célpontokhoz. Más szóval hányat kell ,,vízszintesen'', vagyis kelet-nyugati irányban, illetve ,,függőlegesen'', azaz észak-déli irányban lépnünk, ha a város egyik pontjából el szeretnénk jutni egy másikba, méghozzá a lehető legrövidebb úton. Az egyszerűség kedvéért a továbbiakban ezeket az irányokat a ,,felfelé'', vagy ,,lefelé'', illetve ,,jobbra'', ,,balra'' kifejezésekkel illetjük. Ha $O$-ból el akarunk menni $B$-be, ezt többféleképpen is megtehetjük, például a 2. ábrán jelzett utakon, ekkor mindkét esetben valóban úgy közlekedtünk, mint egy taxi, mivel csak vízszintesen és függőlegesen mozogtunk. Legyenek $O$ és $B$ egy koordináta-rendszernek a pontjai, ahol $O=\left(o_1;o_2\right)$ és $B=\left(b_1;b_2\right)$. Ekkor $O$-ból $B$-be haladva legalább $|o_1-b_1|$ hosszú utat kell vízszintesen megtennünk és legalább $|o_2-b_2|$ utat kell megtennünk függőlegesen. A felírt szakaszok hosszainak az összege fogja megadni, hogy milyen hosszú úton jutunk el az egyik pontból a másikba, ha a lehető legrövidebben megyünk. Ezek után felírhatjuk a két pont ,,taxi távolságát'' megadó képletet: $d_T\left(O;B\right)=|b_1-o_1|+|b_2-o_2|$. Természetesen a képlet úgy is használható, ha a pontok koordinátái nem egészek, de az egyszerűség kedvéért a továbbiakban csak egész koordinátájú pontokkal foglalkozunk. 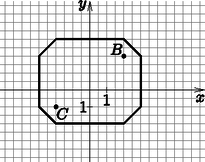Jelölje a későbbiekben $d_E$ az euklideszi, míg $d_T$ a taxi geometriabeli távolságot. Nézzük meg az 1. ábrán az $A=\left(6;0\right)$ és $B=\left(4;3\right)$ pontok euklideszi távolságát az origótól. Az $A$ pont esetében ez nyilván $d_E\left(A;O\right)=6$, míg a $B$ pont esetében a Pitagorasz-tétel segítségével tudjuk azt kiszámolni, azaz $d_E\left(B;O\right)=\sqrt[]{{\left(0-4\right)}^2+{\left(0-3\right)}^2}=5$. Ebből következik, hogy $d_E\left(B;O\right)<d_E\left(A;O\right)$, tehát az euklideszi távolság szerint $B$ közelebb van $O$-hoz, mint az $A$ pont. A következőkben számoljuk ki ugyanezen pontok között a taxi távolságot is. Ahhoz, hogy az $O$ ponttól eljussunk $A$-ba $6$, míg a $B$ pont esetében $3+4=7$ háztömbnyi távolságot kell megtennünk. Vagyis $d_T\left(A;O\right)=6$ és $d_T\left(B;O\right)=3+4=7$, ahol az utóbbi esetben az összeg első tagja a függőlegesen, a második pedig a vízszintesen megtett út. Megfigyelhető, hogy $d_T\left(B;O\right)>d_T\left(A;O\right)$, tehát a taxi távolság szerint $A$ közelebb van $O$-hoz, mint $B$. Érdemes ezután megvizsgálni, mit mondhatunk általában a kétféle távolság nagyságának kapcsolatáról.   1. állítás. Két pont euklideszi távolsága legfeljebb akkora, mint a taxi távolságuk, ami pedig legfeljebb az euklideszi távolság $\sqrt[]{2}$-szerese.   Bizonyítás. Legyenek $X=\left(x_1;x_2\right)$ és $Y=\left(y_1;y_2\right)$ a sík pontjai. Ekkor az abszolútérték nemnegativitásának köszönhetően $2|x_1-y_1||x_2-y_2|\ge 0$ teljesül. Adjunk hozzá az egyenlőtlenség mindkét oldalához ${|x_1-y_1|}^2+{|x_2-y_2|}^2$-et, ekkor a következőt kapjuk: $\begin{array}{c}{\displaystyle 2|x_1-y_1||x_2-y_2|+{|x_1-y_1|}^2+{|x_2-y_2|}^2\ge {|x_1-y_1|}^2+{|x_2-y_2|}^2\mathrm{.}}\end{array}$ Mivel az egyenlőtlenség bal oldalán egy teljes négyzet található, így azt összevonva, $\begin{array}{c}{\displaystyle {\left(|x_1-y_1|+|x_2-y_2|\right)}^2\ge {\left(x_1-y_1\right)}^2+{\left(x_2-y_2\right)}^2\mathrm{.}}\end{array}$ Mindkét oldalon gyököt vonva, az egyszerűsítés után azt kapjuk, hogy $\begin{array}{c}{\displaystyle |x_1-y_1|+|x_2-y_2|\ge \sqrt[]{{\left(x_1-y_1\right)}^2+{\left(x_2-y_2\right)}^2}\mathrm{,}}\end{array}$ ami nem más, mint $d_T\ge d_E$. Az euklideszi távolság tehát nagyobb vagy egyenlő, mint a taxi távolság. Egyenlőség pedig csak abban az esetben áll fenn, ha $x_1=y_1$, vagy $x_2=y_2$ teljesül, vagyis $x$ és $y$ egy (vízszintes vagy függőleges) egyenesen helyezkednek el. Hasonlóan, az ${\left(|x_1-x_2|-|y_1-y_2|\right)}^2\ge 0$ egyenlőtlenség rendezésével ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {|x_1-x_2|}^2+{|y_1-y_2|}^2}& {\displaystyle \ge 2|x_1-x_2|\cdot |y_1-y_2|\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\left({\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2\right)}& {\displaystyle \ge {\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2+2|x_1-x_2|\cdot |y_1-y_2|\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\left({\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2\right)}& {\displaystyle \ge {\left(|x_1-x_2|+|y_1-y_2|\right)}^2\mathrm{,}}\hfill \end{array}}$ négyzetgyököt vonva pedig $\begin{array}{c}{\displaystyle \sqrt[]{2}\sqrt[]{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}\ge |x_1-x_2|+|y_1-y_2|\mathrm{,}}\end{array}$ azaz valóban $\sqrt[]{2}{d}_E\ge d_T$. Ezzel az állítást beláttuk.  $\square$ Meg kell még jegyeznünk, hogy a fentiekben csak olyan pontokkal foglalkoztunk, amelyek egész számú koordinátákkal rendelkeznek, de ugyanúgy, ahogy bármely, akár nem egész koordinátájú pontok esetében is ki tudjuk számolni azok euklideszi távolságát, így a taxi távolságot is. Bármely két pontnak van tehát taxi távolsága, attól függetlenül, hogy azok két utca találkozásánál vannak vagy sem. A következőkben nézzünk meg néhány ,,gyakorlati'' problémát, amelyek megoldásában a taxi geometriát célszerű alkalmazni az euklideszi helyett. 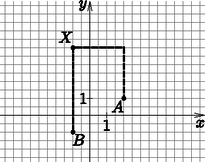  3. ábra     1. feladat. Az ideális városban bejelentés érkezett a rendőrségi diszpécserhez, miszerint baleset történt az $X=\left(-1;4\right)$ pontban. Két járőrkocsi is a baleset közelében van, az egyik az $A=\left(2;1\right)$, míg a másik a $B=\left(-1;-1\right)$ helyen. Melyik kocsit küldjék a baleset helyszínére?   Megoldás. Vegyünk egy koordináta-rendszert és jelöljük rajta az $X=\left(-1;4\right)$, $A=\left(2;1\right)$ és $B=\left(-1;-1\right)$ pontokat. Mivel azt szeretnénk, hogy egy járőr minél előbb a helyszínre érjen, a legközelebbi kocsit kell odaküldenünk. Ehhez ki kell számolnunk, hogy $A$ és $B$ milyen távolságra vannak $X$-től a taxi távolság szerint. Nézzük meg először az $A$ és $X$ közötti távolságot, ez az előzőekben leírtak alapján úgy számolható ki, hogy összeadjuk, hogy hány háztömböt kell vízszintesen, illetve függőlegesen haladnunk $A$-tól $X$-ig, vagyis $d_T\left(A;X\right)=|2-\left(-1\right)|+|1-4|=6$. Hasonlóan járjunk el a $B$ és $X$ pontok esetében, azaz $d_T\left(B;X\right)=|-1-\left(-1\right)|+|-1-4|=5$. Ezek alapján azt kaptuk, hogy az $A$-val jelölt rendőrautó $6$, míg a $B$-vel jelölt rendőrautó $5$ háztömbnyi távolságra van a baleset helyszínétől. A diszpécser a $B$ kocsit fogja a baleset helyszínére küldeni, mivel az közelebb van ahhoz, így gyorsabban fog odaérni (feltéve persze, hogy a városban mindenütt ugyanakkora a forgalom).   2. feladat. Anna és Balázs lakást keresnek az ideális városban, Anna egy bankban dolgozik, amely az $A=\left(-3;-1\right)$ kereszteződésben található, míg Balázs egy iskolában, amely $B=\left(3;3\right)$-ban van. Úgy döntöttek, hogy olyan helyen keresnek albérletet, ahol Anna munkahelyétől a lakásig és Balázs munkahelyétől a lakásig vett távolságok összege minimális. Mely kereszteződésekben keressenek lakást?   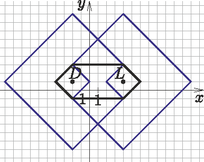Megoldás. Vegyünk egy koordináta-rendszert, ahol jelöljük Anna munkahelyét $A$-val, Balázsét $B$-vel és $L$-lel a keresendő lakást. A kérdés matematikailag megfogalmazva az, hogy keressük azon $L$ pontokat, amelyekre a $d_T\left(A;L\right)+d_T\left(B;L\right)$ kifejezés minimális. Ahhoz, hogy $A$-ból $B$-be eljussunk a legrövidebb úton, függőlegesen felfelé kell haladnunk $4$ háztömböt és vízszintesen jobbra $6$-ot. Ezt többféleképpen is megtehetjük attól függően, hogy melyik kereszteződésben melyik irányt választjuk a kettő közül. Az összes lehetséges útvonalat jelölve a 4. ábrán lévő téglalapot kapjuk. Ha ennek a belsejében vagy a határán lévő kereszteződésekben keresünk albérletet, akkor az $A$-tól és $B$-től vett távolságának az összege $10$, hiszen ekkor $A$-tól az albérletig és az albérlettől $B$-ig megtett út éppen $A$ és $B$ távolsága. Tekintsünk most egy tetszőleges pontot a kapott téglalapon kívül az első síknegyedben és tegyük fel, hogy ez a keresett lakás, legyen ez például az $L=\left(1;5\right)$. Ekkor $L$-nek az $A$-tól vett távolsága $d_T\left(A;L\right)=|-3-1|+|-1-5|=10$ és $B$-től $d_T\left(B;L\right)=|3-1|+|3-5|=4$. Vagyis ebben az esetben $d_T\left(A;L\right)+d_T\left(B;L\right)=14$. Ez láthatóan több, mintha az előzőekben megbeszélt területen béreltek volna lakást, hiszen itt az $A$ pontból kiindulva $4$ háztömbnyit kell gyalogolnunk ,,felfelé'' ahhoz, hogy eljussunk a $B$-n átmenő vízszintes (kelet-nyugati) egyenesig (utcáig), de mivel az $L$ ,,feljebb'' található, ezért még $2$-t kell megtennünk ebbe az irányba. Jobbra ugyan kevesebbet kell mennünk, $4$ háztömbnyit, viszont a ,,hiányzó'' $2$ háztömböt $B$-nek kell megtennie ,,balra'' és ezen felül $B$-nek is haladnia kell ugyanannyit ,,felfelé'', mint amennyi extra háztömböt kellett $A$-nak. Összeszámolva, többet kellett függőlegesen és vízszintesen is haladnunk, mintha a téglalap belsejéből, vagy határáról választottunk volna egy pontot. Hasonló eredményeket kapunk, ha a többi síknegyedből választunk pontokat a téglalapon kívül. A $d_T\left(A;L\right)+d_T\left(B;L\right)$ összeg minimuma tehát $10$, és a minimumot adó pontok a 4. ábrán jelölt téglalap pontjai. 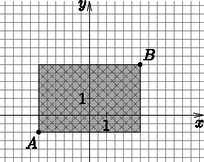  4. ábra     2. A kör Az euklideszi geometriában a síkon egy kört vagy körvonalat a következőképpen definiálunk.   1. definíció. A körvonal a sík azon pontjainak a mértani helye, amelyek a sík egy adott pontjától adott távolságra helyezkednek el. Az adott pont a kör középpontja, míg a távolságot a kör sugarának nevezzük. 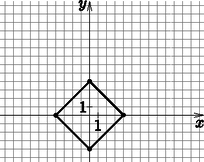    5. ábra   Ha a megszokott euklideszi távolságot vesszük figyelembe, akkor egy ,,kör'' alakú alakzatot kapunk, viszont a taxi távolság esetében a kör már nem így fog kinézni, azaz nem lesz kör alakú. Ahhoz, hogy megtudjuk, hogy milyen lesz az új alakzatunk, vegyünk egy $\left(x_0;y_0\right)$ pontot és keressük meg azokat az $\left(x;y\right)$ pontokat, amelyek tőle adott $r$ taxi távolságra helyezkednek el. Vagyis $d_T\left(\left(x_0;y_0\right)\mathrm{,}\left(x;y\right)\right)=|x_0-x|+|y_0-y|=r$. Nézzük meg az abszolútértékek feloldására szolgáló négy esetet és az általuk meghatározott alakzatokat. Ha $x_0\ge x$ és $y_0\ge y$, akkor elhagyva az abszolútérték jeleket az egyenletünk $x_0-x+y_0-y=r$, amelyet átrendezve $y=-x+x_0+y_0-r$. Az egyenlet az $x_0\ge x$ és $y_0\ge y$ feltételek mellett egy szakaszt határoz meg, amelynek pontjai $r$ taxi távolságra vannak az $\left(x_0;y_0\right)$ ponttól és végpontjai $\left(x_0-r;y_0\right)$ és $\left(x_0;y_0-r\right)$. Ha $x_0\le x$ és $y_0\ge y$, akkor az egyenlet $\begin{array}{c}{\displaystyle -\left(x_0-x\right)+y_0-y=r\mathrm{,}\text{átrendezve}y=x-x_0+y_0-r\mathrm{.}}\end{array}$ Ennek a szakasznak a végpontjai az $\left(x_0+r;y_0\right)$ és az $\left(x_0;y_0-r\right)$. Ha $x_0\le x$ és $y_0\le y$, akkor a $-\left(x_0-x\right)-\left(y_0-y\right)=r$ egyenletet kapjuk, amelyet átrendezve az $y=-x+x_0+y_0+r$ kifejezést kapjuk. A szakasz végpontjai ebben az esetben $\left(x_0+r;y_0\right)$ és $\left(x_0;y_0+r\right)$. Ha $x_0\ge x$ és $y_0\le y$, akkor az egyenlet $x_0-x-\left(y_0-y\right)=r$, amelyet ha átrendezünk, az $y=x-x_0+y_0+r$ egyenletet kapjuk. Ekkor a kapott szakasz végpontjai $\left(x_0;y_0+r\right)$ és $\left(x_0-r;y_0\right)$. Vegyük észre, hogy az egyes szakaszok végpontjai megegyeznek, így egy négyzetet határoznak meg, amelynek a csúcsai az $\left(x_0;y_0-r\right)$, $\left(x_0+r;y_0\right)$, $\left(x_0;y_0+r\right)$ és az $\left(x_0-r;y_0\right)$ pontok lesznek. A kör a taxi geometriában tehát egy euklideszi értelemben vett négyzet, amelynek csúcsai az előbbi pontok. Alkalmazzuk a fentiekben leírtakat néhány feladatban.   3. feladat. Eszter az ideális városban járt, amikor az $E=\left(2;1\right)$ pontban észrevette, hogy fogyóban van az üzemanyaga. Tudja, hogy $5$ háztömb távolságban található egy benzinkút. Mely pontokban helyezkedhet el a benzinkút?   Megoldás. A koordináta-rendszerben vegyük fel az $E$ pontot. Azokat a pontokat keressük, amelyek $5$ háztömb távolságra vannak az $E$-től, vagyis egy adott ponttól egyenlő távolságra lévő pontokat. Ez azt jelenti, hogy egy $E$ középpontú $5$ sugarú taxi kört akarunk meghatározni. Ekkor a $\left(2;1+5\right)=\left(2;6\right)$, $\left(2;1-5\right)=\left(2;-4\right)$, $\left(2+5;1\right)=\left(7;1\right)$ és $\left(2-5;1\right)=\left(-3;1\right)$ pontok meghatároznak egy euklideszi értelemben vett négyzetet, vagyis az $E$ középpontú $5$ sugarú taxi kört. A taxi körvonalat alkotó pontok mindegyike tehát $5$ taxi távolságra van Eszter jelenlegi helyétől, vagyis megállapíthatjuk, hogy a keresett benzinkút a taxi körvonal valamelyik pontjában helyezkedik el. Ha az $y$-tengellyel párhuzamosan mozdítjuk el a pontot, akkor a távolsága $E$-től nőni fog. Ha viszont az $x$-tengellyel párhuzamosan indulunk el, akkor az egyik irányba csökkenni, a másikba pedig ismételten nőni fog a távolság a két pont között. A következőkben próbáljuk meg egy, a ponton átmenő $1$ meredekségű egyenesen mozgatni a pontunkat, ekkor ha a negyedik síknegyed felé haladunk, akkor ismét azt fogjuk tapasztalni, hogy a távolság egyre csak nő. Azonban, ha a másik irányt választjuk, akkor a távolságunk nem fog változni, vagyis ugyanúgy $5$ marad, egészen a $\left(2;6\right)$ csúcsig, onnantól kezdve az egyenesen tovább haladva a távolságuk ismét nőni fog. Ezek a pontok mind jó távolságra lesznek $E$-től. Most nézzük meg az ugyanezen a ponton áthaladó $-1$ meredekségű egyenest. Ebben az esetben ha az első síknegyed felé megyünk, akkor a távolság egyre csak nő, viszont a másik irányban haladva újra jó pontokat kapunk, mivel ezek ugyanúgy $5$ háztömbnyire lesznek $E$-től. Ismét csak egy csúcsig, méghozzá a $\left(2;-4\right)$-ig mehetünk, mivel ha tovább folytatjuk utunkat az egyenesen a távolság megint nőni fog. Ezt a gondolatmenetet alkalmazva a $\left(-3;1\right)$ pontra hasonló alakzatot fogunk kapni. Ha vesszük az unióját a másik pontnál kapott alakzattal egy négyzetet fogunk kapni, amelynek az összes pontja pontosan $5$ távolságra lesz Eszter jelenlegi helyétől, vagyis ezen a vonalon kell elhelyezkednie a benzinkútnak.   4. feladat. Péter az ideális városban dolgozik egy irodában, amely az $I=\left(1;2\right)$ pontban helyezkedik el. Minden nap eljár ebédelni, de mivel nem szeretne túl messzire menni a munkahelyétől, így eldöntötte, hogy legfeljebb $3$ háztömbnyire hajlandó éttermet keresni. Hol találhatók azok az éttermek a városban, ahol Péter elfogyaszthatja az ebédjét?   Megoldás. Vegyük fel a koordináta-rendszerünkben az irodát, ahol Péter dolgozik. Keressük meg azokat a pontokat, amelyek pontosan $3$ távolságra vannak $I$-től a taxi geometriában. A fentiekben leírtak alapján tudjuk, hogy azok az $\begin{array}{c}{\displaystyle \left(1;2+3\right)=\left(1;5\right)\mathrm{,}\left(1;2-3\right)=\left(1;-1\right)\mathrm{,}\left(1+3;2\right)=\left(4;2\right)\text{ és }\left(1-3;2\right)=\left(-2;5\right)}\end{array}$ pontok által meghatározott euklideszi értelemben vett négyzetlap pontjai. Péter a négyzetlap pontjai között kereshet éttermet.   5. feladat. Egy építész cég szeretne egy apartmanházat felépíteni, méghozzá úgy, hogy az legfeljebb $5$ háztömb távolságban legyen a $B=\left(-3;0\right)$ pontban található bevásárlóközponttól, illetve, hogy legfeljebb $4$ háztömbnyire legyen a teniszpályától, amely a $T=\left(2;2\right)$ pontban helyezkedik el. Hova építheti fel a házat, hogy mindkettő feltétel teljesüljön?   Megoldás. Gondoljuk meg, hogy hogyan is oldanánk meg a feladatot a szokásos távolságfüggvény mellett. Vegyünk fel egy koordináta-rendszert és abban jelöljük a $B$ és $T$ pontokat a megfelelő helyen. A feladat szerint a $B$ ponttól legfeljebb $5$ háztömb távolságra építkezhetünk, ezen pontok halmaza ekkor egy körlap lesz. Ugyanígy járhatunk el a $T$ pont esetében is. Ekkor kaptunk két körlapot, mindkét feltételünk akkor fog egyszerre teljesülni, hogyha a két körlap metszetében építkezünk. Ha most a taxi metrikában oldjuk meg a feladatot, hasonlóan kell eljárnunk, azzal a különbséggel, hogy az előzőek alapján tudjuk, hogy a körlapok ebben az esetben négyzetlapok lesznek, méghozzá pontosan úgy, mint a 6. ábrán. Ha a két négyzetlap metszetében keres az építész cég helyet az apartmanház felépítéséhez, biztosan teljesülni fog mindkét feltétel. 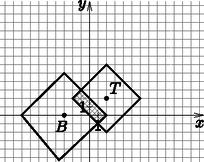  6. ábra     6. feladat. Egy telefontársaság (a $20$. század első felében $\text{...}$) telefonfülkéket szeretne telepíteni az ideális városba, méghozzá úgy, hogy mindenki, aki legfeljebb $12$ háztömbnyi távolságra lakik a városközponttól, legfeljebb $4$ háztömbnyire legyen egy telefonfülkétől. Hová tegye a telefonfülkéket a cég?   Megoldás. Vegyünk fel egy koordináta-rendszert, ahol legyen az origó a városközpont. Ettől legfeljebb $12$ háztömbnyi távolságnyira szeretnénk a telefonfülkéket telepíteni. Nézzük meg először azokat a pontokat, amelyek pontosan ekkora távolságra lesznek az origótól. Egy adott ponttól egyenlő távolságra lévő pontok halmazát, azaz egy taxi kört fogunk ismét keresni. Ha ezt tudjuk, akkor felírhatjuk a taxi kör csúcsait: $\left(12;0\right)$, $\left(-12;0\right)$, $\left(0;12\right)$ és $\left(0;-12\right)$, ezek megadják a $12$ sugarú, origó centrumú taxi körlapot. A kapott taxi kört fel tudjuk osztani, ahogyan a 7. ábra is mutatja, $9$ egybevágó részre. Látható, hogy az így kapott euklideszi értelemben vett négyszögek $4$ egységnyi sugarú taxi körök. Ha ezen körök mindegyikébe elhelyezünk egy-egy fülkét, akkor a $12$ sugarú körlap egész területére teljesül, hogy az ott élők legfeljebb $4$ háztömbnyire vannak a legközelebbi fülkétől. Azok, akik a taxi körök határán élnek $2$; azok, akik a négyzetek megfelelő sarkaiban élnek $4$ fülke közül is választhatnak. Ahogyan a 8. ábrán is láthatjuk, $9$ fülke elég lesz a terület teljes lefedéséhez. 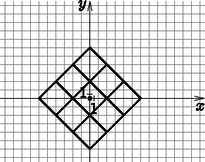  7. ábra 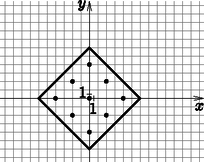    8. 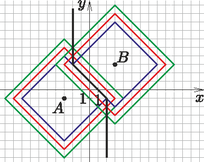ábra     7. feladat. Anna és Balázs albérletet keresnek. Egyetlen feltételhez ragaszkodnak, méghozzá ahhoz, hogy mindketten egyenlő távolságra lakjanak a munkahelyüktől, vagyis Anna a banktól, amely az $A=\left(-3;-1\right)$ pontban található és Balázs az iskolától, amely a $B=\left(3;3\right)$ pontban van.   9. ábra   Megoldás. Ahogy már a 2. feladatban is kiszámoltuk $d_T\left(A;B\right)=|-3-3|+|-1-3|=10$, ennek a fele $5$, vagyis az albérlet legalább $5$ taxi távolságra kell, hogy legyen $A$-tól és $B$-től is. Keressük meg először az $A$ és $B$ pontoktól $5$ háztömbnyi távolságra lévő pontokat. Egy adott ponttól adott távolságra lévő pontokat keresünk, vagyis egy-egy taxi kört. Az $A$ pontnál a $\left(-3;4\right)$, $\left(-8;-1\right)$, $\left(-3;-6\right)$ és $\left(2;-1\right)$ pontok, míg a $B$ esetében a $\left(3;8\right)$, $\left(-2;3\right)$, $\left(3;-2\right)$ és $\left(8;3\right)$ pontok határozzák meg az $5$ sugarú taxi köröket. A két taxi kör az oldalszakaszaik egy részében fognak érintkezni, ahogyan az a 9. ábrán is látható a belső négyzetek esetében, ezek azok a pontok, amelyekre teljesül, hogy mindkét ponttól $5$ távolságra vannak. Ha Anna és Balázs ezen a szakaszon keres lakást, akkor biztosan teljesülni fog rá a feltételük. Nemcsak az $A$-tól és $B$-től $5$ taxi távolságra lévő pontok lesznek megfelelőek, hanem azok is, amelyek $\mathrm{6,7,}\text{...}$ taxi távolságra vannak tőlük. Ha ezeket a taxi köröket is felrajzoljuk, akkor láthatjuk a 9. ábrán a két középső, illetve a két külső négyzeten, hogy 2-2 pontban fogják egymást metszeni, vagyis ezek azok a pontok, amelyek $A$-tól és $B$-től is egyenlő távolságra vannak. Ha az összes jó pontot megtaláltuk, akkor a fekete töröttvonalat fogjuk megkapni. Annának és Balázsnak ezen a vonalon kell albérletet keresniük, ha azt akarják, hogy az mindkettejük munkahelyétől egyenlő távolságra legyen. Mozgassuk a $C$-t és nézzük meg, hogyan változik az $A$-hoz viszonyított távolsága. Ha az $y$-tengellyel párhuzamosan mozdítom el bármelyik irányba, akkor a távolság nőni fog. Ha az $x$-tengellyel párhuzamosan teszem ugyanezt, akkor egyik irányba csökken, míg a másikba nő a távolsága az $A$-tól. Ezek után próbáljunk meg ferdén, a ponton átmenő, euklideszi értelemben vett $1$ meredekségű egyenes mentén haladni. Ha távolodunk az $y$-tengelytől, akkor a távolság ismét nő. Azonban, ha közeledünk felé, akkor nem változik, $5$ marad egészen addig, míg el nem érünk az $A$ pont vonalába, utána a távolság újra nőni fog. A $-1$ meredekségű egyenesen haladva hasonló eredményeket kapunk. Vegyük most a $D=\left(-8;-1\right)$ pontot és mozgassuk úgy, mint $C$-t. A $C$ és $D$ pontok mozgatása által egy négyzetet kaptunk és megtaláltuk az összes olyan pontot, amely $5$ távolságra lesz $A$-tól. Ugyanezt szeretnénk megtenni $B$-vel is, ahol ugyanúgy egy négyzetet fogunk kapni. A két négyszög egyik oldalegyenese egybeesik, ahogyan az a 9. ábrán is látszik. Tehát ezek lesznek azok a pontok a téglalapon belül, amelyekre teljesül a feltételünk. A követezőkben nézzük meg azokat a pontokat, amelyek $6$ háztömbnyi távolságra lesznek a két munkahelytől. Az előző eljárást alkalmazva, azt tapasztaljuk, hogy ismét két négyzetet kaptunk, amelyeket az ábrán kékkel jelöltünk. Ezeknek a metszéspontjai lesznek azok a pontok, amelyek $A$-tól és $B$-től egyenlő távolságra lesznek. Ha az eddigiekhez hasonlóan folytatjuk és megnézzük a $\mathrm{7,8,}\text{...}$ távolságra lévő pontokat is, akkor az ábrán feketével jelzett vonalat kapjuk. Vagyis azok lesznek azok a pontok, amelyek egyenlő távolságra lesznek Anna és Balázs munkahelyétől, itt kell maguknak albérletet keresni, ha azt szeretnék, hogy a fenti feltétel teljesüljön.   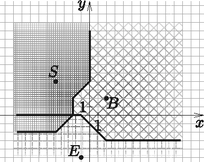8. feladat. Az ideális városban három középiskola is van: a Széchenyi az $S=\left(-4;3\right)$ pontban, a Berzsenyi a $B=\left(2;1\right)$ pontban, az Eötvös az $E=\left(-1;-6\right)$ pontban. A város egyes pontjain lakó gyerekek melyik középiskola diákjai, ha mindenki a számára legközelebb lévőbe jár?   Megoldás. Ebben a feladatban adott három ponttól egyenlő távolságra lévő pontokat szeretnénk megtalálni. Számoljuk ki először a pontok távolságát egymástól: $d_T\left(S;B\right)=|-4-2|+|3-1|=8$, $d_T\left(S;E\right)=|-4+1|+|3+6|=12$ és $d_T\left(E;B\right)=|-1-2|+|-6-1|=10$. Nézzük meg, hogy kik lesznek azok, akik válaszhatnak, hogy melyik iskolába járjanak, mivel két iskolától is egyenlő távolságra laknak. Vegyük a Széchenyi és a Berzsenyi iskolákat, vagyis az $S=\left(-4;3\right)$ és $B=\left(2;1\right)$ pontokat a koordináta-rendszerünkben és nézzük meg, melyek azok a pontok, amelyek ugyanannyi távolságra vannak tőlük. Alkalmazzuk a 7. feladatban tanultakat, így kapni fogunk egy szakaszt, amely a $\left(-2;2\right)$ és $\left(0;4\right)$ pontokra illeszkedik, valamint az ezekből a pontokból kiinduló félegyeneseket, amelyek párhuzamosak a tengelyekkel. Ha ugyanezt az eljárást használjuk az $S$ és $E$, illetve $E$ és $B$ esetében, hasonló alakzatokat kapunk, annyi változtatással, hogy mindkét esetben, ha azokat a pontokat keressük, amelyek nagyobb távolságra vannak mindkét ponttól, mint a távolságuknak a fele, ezúttal nem ,,felfele'' és ,,lefele'' keressük, hanem az $x$-tengellyel párhuzamosan jobb, illetve bal irányban. Végül a 10. ábrát kapjuk, ahol látható, hogy a töröttvonalak metszeni fogják egymást a $\left(-2;0\right)$ pontban. Ez azt jelenti, hogy akik itt laknak, azok három, a töröttvonal többi pontján lakó gyerekek pedig kettő iskola közül választhatnak; míg azok, akik a különböző módon satírozott részeken élnek, nem választhatnak, ők a hozzájuk legközelebbi iskolába járnak.   10. ábra     3. Az ellipszis Az euklideszi síkon egy ellipszist a következőképpen definiálunk.   2. definíció. Az ellipszis azoknak a síkbeli pontoknak a mértani helye, amelyeknek a síkon két adott ponttól mért távolságaik összege állandó, és ez az állandó nagyobb, mint a két pont távolsága. A két adott pontot fókuszpontoknak hívjuk. Ahogy azt már a kör esetében is láthattuk, a távolságfüggvény megváltozásával az alakzat képe is módosulni fog. Először gondoljuk meg, hogyan is rajzolnánk fel egy euklideszi értelemben vett ellipszist. A taxi ellipszis is hasonló módon rajzolható fel, azzal a különséggel, hogy ebben az esetben körök helyett négyzeteket fogunk összemetszeni. Hogy ez hogyan is működik, egy feladaton keresztül nézzük meg.   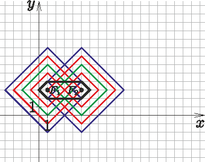9. feladat. Legyenek a fókuszok az $F_1=\left(1;3\right)$ és $F_2=\left(5;3\right)$ pontok. Azokat a $P$ pontokat keressük a síkon, amelyeknek a fókuszoktól vett távolságösszege $6$ egység.   Megoldás. A feladat feltétele: $d_T\left(P;F_1\right)+d_T\left(P;F_2\right)=6$. A $6$-ot például fel tudjuk írni a $4$ és $2$ összegeként. Ekkor legyen $d_T\left(P;F_1\right)=4$ és $d_T\left(P;F_2\right)=2$. Ez azt jelenti, hogy mindkét esetben egy adott pontól adott távolságra lévő pontok halmazát keressük, vagyis taxi köröket, amelyeknek a centruma az adott fókusz, a sugara pedig a távolság. Ha ezeket felrajzoljuk, akkor a metszéspontjaikra igaz, hogy $F_1$-től $4$ és $F_2$-től $2$ távolságra vannak, vagyis ezek a pontok rajta lesznek a keresett taxi ellipszisünkön. Ezt az eljárást folytatjuk úgy, hogy közben olyan sugarú taxi köröket metszünk össze, amelyek sugarainak az összege $6$. Az $1$ és $5$ sugarú körök esetében egy érdekes dolgot figyelhetünk meg. Ezek ugyanis nem egy vagy két pontban fogják metszeni egymást, hanem a kisebbik négyszög két teljes oldalszakaszában. Ha az összes lehetséges kört felrajzoltuk, akkor a 11. ábrán látható taxi ellipszist fogjuk kapni.   11. 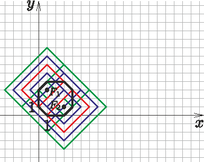ábra   Ezek alapján azt feltételezhetnénk, hogy egy taxi ellipszis általában egy hatszög lesz, azonban ez nincs mindig így. Változtassuk meg a fókuszpontokat úgy, hogy azoknak egyik koordinátája se egyezzen meg a másik megfelelő koordinátájával. Ha a 9. feladatban lévő fókuszok helyett például az $F_1=\left(1;3\right)$ és $F_2=\left(3;1\right)$ pontokkal oldjuk meg a feladatot, akkor a 12. ábrát kapjuk, amelyen jól látható, hogy ezúttal egy nyolcszög a megoldás. Tekintsük a 11. és 12. ábrákat és figyeljük meg a kapcsolatot az ellipszis vízszintes és függőleges oldalai és a fókuszok által meghatározott téglalap között. Ha közelítjük egymáshoz a két fókuszt, akkor egyre kisebb lesz a téglalap, valamint az ellipszis vízszintes és függőleges oldalai is, egészen addig, amíg a két pont meg nem egyezik, amikor is az ellipszisből egy taxi kört kapunk. Hasonló jelenség figyelhető meg az euklideszi értelemben vett ellipszis esetében is, hiszen ahogy közelítjük a két fókuszt egymáshoz, annál jobban fog az alakzat egy körre hasonlítani.   12. ábra   Nézzük meg, hogyan tudjuk alkalmazni a fentiekben leírtakat néhány feladatban.   10. feladat. Csongor, aki a $C=\left(-2;-1\right)$ pontban lakik az ideális városban, minden reggel futni jár. Egy barátja, akinek otthona a $B=\left(2;2\right)$ pontban van, úgy dönt, hogy csatlakozik hozzá. Elhatározzák, hogy mindig a város határán fognak találkozni. Kiszámolták, hogy ez csak úgy sikerülhet, ha a Csongor és barátja által futott táv pontosan $9$ háztömbnyi. Melyek lesznek a város szélét jelző pontok?   Megoldás. Vegyünk fel egy koordináta-rendszert és abban jelöljük a $C=\left(-2;-1\right)$ és $B=\left(2;2\right)$ pontokat. Azokat a $P$ pontokat keressük, amelyekre teljesül, hogy $d_T\left(P;C\right)+d_T\left(P;B\right)=9$, amely egy taxi ellipszis. Legyen például $d_T\left(P;C\right)=1$ és $d_T\left(P;B\right)=8$. Ekkor ez azt jelenti, hogy a $B$ és $C$ pontoktól adott távolságra lévő pontok halmazát keressük, vagyis taxi köröket. Ha ábrázoljuk először a $C$-től $1$ és a $B$-től $8$ taxi távolságra lévő pontokat, a két taxi kör két metszéspontjára igaz lesz a feltételünk, amely ebben az esetben nem két metszéspont lesz, hanem a kis taxi kör két teljes oldalszakasza, mivel azok teljes egészében a nagy taxi kör oldalszakaszainak részei. Ugyanezt megtehetjük fordítva is, miszerint ha felrajzoljuk a $C$-től $8$ és a $B$-től $1$ taxi távolságra lévő pontokat, ekkor ismét két oldalszakaszt fogunk kapni. Nézzük meg, hogy a $9$ még hányféleképpen bontható fel két szám összegére. Ha a $2$ és $7$ sugarú taxi körök metszik egymást, akkor két metszéspontot fogunk kapni és ugyanez történik, ha a $3$ és $6$ sugarú taxi körök esetét vizsgáljuk meg. Ha azonban a $4$ és $5$ sugarú taxi körök metszetét képezzük, azok egy pontban és két oldalszakasz egy kis szakaszán fogják metszeni egymást. Ezek a pontok egy taxi ellipszist fognak alkotni, ahogyan azt a 13. ábrán is láthatjuk. Ezek lesznek a város szélét jelző pontok.   13. ábra     11. feladat. Dóra, aki az ideális városban lakik, irodát keres a vállalkozásának. Úgy szeretne helyet találni, hogy a $D=\left(-2;1\right)$ pontban elhelyezkedő lakásától az irodáig, valamint az $L=\left(4;1\right)$ pontban lévő óvodától, ahova a lánya jár, az irodáig legfeljebb $10$ háztömbnyi távolságot kelljen megtennie. Hol keressen irodát?   Megoldás. A koordináta-rendszerben vegyük fel a $D$ és $L$ pontokat. Azokat a $P$ pontokat keressük, amelyekre teljesül, hogy a $D$-től és $L$-től való távolságok összege kisebb vagy egyenlő, mint $10$, vagyis $d_T\left(P;D\right)+d_T\left(P;L\right)\le 10$. Keressük meg elsőként azokat a pontokat, amelyekre a távolságok összege pontosan $10$ háztömbnyi. A $10$ többféleképpen is felírható két pozitív egész szám összegeként. Ha megnézzük először az $1$ és $9$ sugarú taxi köröket, észrevehetjük, hogy ezeknek nincs egyetlen közös pontjuk se. A $2+8$ felbontás esetében rajzoljuk fel a $D$ középpontú $2$ sugarú, és az $L$ centrumú $8$ sugarú taxi köröket. Azt tapasztaljuk, hogy ezen négyszögeknek ezúttal nem egy vagy két metszéspontja lesz, hanem a kisebbik kör két teljes oldalát fedi a nagy kör Ezek mind jó pontok lesznek, hiszen teljesül rájuk a feladat feltétele. Ugyanezt meggondolhatjuk fordított esetben is, ahol a $D$ centrumú $8$ sugarú, és az $L$ középpontú $2$ sugarú taxi köröket metsszük össze. Ez annak köszönhető, hogy a két megadott pont egy egyenesre illeszkedik. Az összes többi felbontáshoz tartozó körök két pontban fogják metszeni egymást. Ha az összes lehetséges felbontást ábrázoljuk, akkor a 14. ábrán látható taxi ellipszist fogjuk kapni. Ha Dóra ezen a vonalon talál irodát a vállalkozásának, akkor teljesülni fog rá a feladat feltétele. Azonban megfelelő pontok lesznek azok is, amelyeknek az óvodától, illetve a lakástól vett távolságaik összege kevesebb, mint $10$ háztömb. Ha felrajzolnánk azt az ellipszist, amelyre $d_T\left(P;D\right)+d_T\left(P;L\right)=11$ teljesül, akkor azt tapasztalnánk, hogy része lesz az előző alakzatunk, vagyis minél nagyobb távolságot adunk meg a távolságok összegeként, annál nagyobb ellipsziseket fogunk kapni. Ez azt jelenti, hogy ha azt keressük, hogy hol kevesebb az összeg, mint $10$, akkor annak az ellipszisnek a belső pontjaira lesz igaz az állítás, amelyekre $d_T\left(P;D\right)+d_T\left(P;L\right)<10$ teljesül. Vagyis Dóra ezen a taxi ellipszisen belül is találhat magának megfelelő irodát.   14. ábra     12. feladat. Egy ipari vállalat gyárat szeretne építeni az ideális városban úgy, hogy a távolságok összege a gyártól a $R=\left(5;-1\right)$ pontban elhelyezkedő repülőtérig, illetve a $V=\left(-5;-3\right)$ helyen lévő vasútállomásig legfeljebb $16$ háztömb legyen. A város azonban a zajszabályozás érdekében előírja, hogy a $K=\left(-4;2\right)$-ben elhelyezkedő könyvtár $3$ háztömbös környezetében nem épülhet fel a gyár. Mely területre építkezhet a vállalat?   Megoldás. Helyezzük el a megadott $R=\left(5;-1\right)$ pontban lévő repülőteret, a $V=\left(-5;-3\right)$ helyen lévő vasútállomást és a $K=\left(-4;2\right)$-ben elhelyezkedő könyvtárat egy koordináta-rendszerben. Először jelöljük azokat a pontokat, amelyek $3$ háztömbnyire vannak a könyvtártól, hiszen tudjuk, hogy erre a területre nem épülhet fel gyár. Mivel egy adott ponttól adott távolságra lévő pontokat szeretnénk meghatározni, egy taxi kört fogunk keresni, amelyet a 2. szakaszban leírtak alapján fel tudunk rajzolni. Másodszor pedig azokat a pontokat keressük meg, ahol a távolságok összege gyártól a repülőtérig és a vasútállomásig legfeljebb $16$ háztömb. Vagyis matematikailag átfogalmazva a feladatot, azokat a $P$ pontokat keressük, amelyekre teljesül, hogy $d_T\left(P;R\right)+d_T\left(P;V\right)\le 16$. Ezek alapján megállapíthatjuk, hogy egy taxi ellipszist keresünk, amelynek a fókuszpontjai az $R$ és $V$ pontok és mivel ezek nem egy egyenesre illeszkednek, így a 10. feladatban leírtakhoz hasonlóan meg tudjuk rajzolni az alakzatot. Mivel nekünk nemcsak azok a pontok lesznek jók, amelyekre a távolságaik összege $R$-től és $V$-től pontosan $16$, hanem azok is, amelyekre a távolságösszeg ennél kisebb, ezért ismét az ellipszis belsejében lévő pontok is megfelelőnek bizonyulnak. Látható azonban, hogy a $K$ pont $3$ sugarú köre belemetsz az ellipszislapba. Erről tudjuk, hogy ide nem építkezhetünk, viszont bárhová máshova az ellipszisen belül igen, ahogyan a 15. ábrán is láthatjuk. 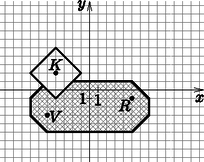  15. ábra     4. Egy további érdekesség Mint ahogyan említettük, a taxi geometria egy sokkal jobb modellt ad a városi közlekedésre az euklideszi geometriával szemben. Tudunk azonban még olyan változtatásokat bevezetni a távolságfüggvényen, amelyekkel az ideális városunk jobban fog hasonlítani egy átlagos városhoz, viszont ezáltal egy kicsit bonyolultabb matematikát is kell alkalmaznunk. Vezessünk be egy tömegközlekedési eszközt, például egy metrót, amely a 16. ábrán látható $L$ vonalon közlekedik és az állomásai az $L$ egyenes egész koordinátájú pontjai. Ha ezt a közlekedési eszközt használjuk, akkor az csökkentheti bizonyos pontok között a távolságot. Tegyük fel, hogy az $A=\left(-3;6\right)$ ponton állunk és szeretnénk eljutni a $P=\left(3;3\right)$ pontban lévő pékségig. Ezt például úgy tehetjük meg, hogy elsétálunk $3$ háztömbnyi távolságot a $\left(-3;3\right)$ pontig majd felülünk a metróra, amellyel eljuthatunk a $\left(3;1\right)$-ig és innentől már csak $2$ háztömböt kell sétálnunk a $P$ pontig. Vagyis a gyalogosan megtett út $A$-ból $P$-be $5$. Természetesen, ha más lett volna a kiindulási helyünk, mondjuk a $B=\left(1;5\right)$ pont, akkor nem kellett volna használni a metrót, gyalogosan is eljuthatunk a kívánt helyre, amely ekkor pontosan $4$ háztömbnyire lesz tőlünk. Nevezzük el az új távolságfüggvényünket a tömegközlekedési eszközünk miatt $d_M$-nek, és definiáljuk a következőképpen: $d_M$ legyen a $d_T\left(X;Y\right)$ távolság, valamint a $d_T\left(X;Q\right)+d_T\left(Y;Q\right)$ kifejezések közül a legkisebb, ahol $Q$ befutja a metróállomásokat (azaz mindig az $X$-hez legközelebbi állomáson szállunk fel és az $Y$-hoz legközelebbin szállunk le). Ekkor 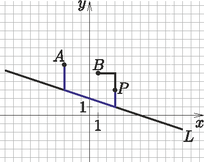$d_M\left(A;P\right)=5$ és $d_M\left(B;P\right)=4$.   16. ábra   Ha azt szeretnénk, hogy az ideális városunk egy még jobb modellt adjon, bevezethetünk több metróvonalat, vagy esetleg telepíthetünk egy tavat a városba. A valódi világ nyújtotta felvethető kérdések száma innentől kezdve végtelen, és jól látható, hogy a felvetődő problémák egy középiskolás számára is érdekesek és megoldhatók.   Irodalomjegyzék [1] Banerjee, Amar Kumar: Metric Spaces and Complex Analysis, New Age International, 2008. [2] Golland, Luise: Karl Menger and Taxicab Geometry in Mathematics Magazine, Vol. 63., No. 5. , pp. 326‐327., Mathematical Association of America, 1990. [3] Greenlees, John: Metric spaces, The University of Sheffield, 2011. [4] Hildebrand, S.K., Milnes, Harold Willis: An Interesting Metric Space in Mathematics Magazine, Vol. 41., No. 5., pp. 244‐247., Mathematical Association of America, 1968. [5] Hong, Min-Chun: Metrics ‐ Lecture Material, The University of Queensland, 2013. [6] Janssen, Christina: Taxicab Geometry: Not the Shortest Ride Across Town (Exploring Conics with a Non-Euclidean Metric), Iowa State University, 2007. [7] Krause, Eugene F.: Taxicab Geometry - An Adventure in Non-Euclidean Geometry, Dover Publications, Inc., New York, 1986. [8] Laczkovich Miklós ‐ T. Sós Vera: Analízis II., Nemzeti Tankönyvkiadó, Budapest, 2007. [9] Shantaram, R.: On an Interesting Metric Space in Mathematics Magazine, Vol. 43., No. 2., pp. 95‐97., Mathematical Association of America, 1970. [10] Reynolds, Barbara E.: Taxicab Geometry, The Pi Mu Epsilon Journal, Worcester, MA. Vol. 7., No. 2., pp. 77‐88., 1980. [11] Sikolya Eszter: Analízis III. előadásjegyzet, ELTE, 2010/2011 őszi félév. [12] Junge, Marius: Metric Spaces, The University of Illinois.