Cím:	Megoldásvázlatok a 2018/3. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Kántor Sándor
Füzet:	2018/április, 203 - 211. oldal	PDF  |  MathML
Hivatkozás(ok):	2018/március: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg a valós számok halmazán az alábbi egyenleteket (ha a megoldás pontos értéke nem racionális szám, akkor közelítő értéket is adjunk): $a)$ $3^{2x+2}+9^{2x+1}=4$.  (5 pont) $b)$ $\text{log}{}_2\left(x-3\right)+{\left(\text{log}{}_4\left(8x-24\right)\right)}^2=6\mathrm{,}25$.  (7 pont)   Megoldás. $a)$ Az egyenlet alakja ekvivalens átalakítások után: $\begin{array}{c}{\displaystyle {\left(3^{2x+1}\right)}^2+3\cdot 3^{2x+1}-4=0.}\end{array}$ Ez a másodfokú egyenlet gyökképlete alapján akkor teljesül, ha $3^{2x+1}=1=3^0$, vagy ha $3^{2x+1}=-4$. Nyilván csak az első egyenlőséget teljesítő $x$ van, ami a 3 alapú exponenciális függvény szigorú monotonitása miatt fennálló $2x+1=0$ egyenletből az $x=-0\mathrm{,}5$ érték. Ezért ez az eredeti egyenlet megoldása. $b)$ Az egyenlet alakja $x>3$ esetén a logaritmus azonosságai alapján $\begin{array}{c}{\displaystyle \text{log}{}_2\left(x-3\right)+{\left(\frac{\text{log}{}_{2}8\left(x-3\right)}{\text{log}{}_{2}4}\right)}^2=6\mathrm{,}\mathrm{25,}}\end{array}$ és további ekvivalens átalakításokkal: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4\text{log}{}_2\left(x-3\right)+{\left(3+\text{log}{}_2\left(x-3\right)\right)}^2}& {\displaystyle =\mathrm{25,}}\hfill \\ \hfill {\displaystyle {\left(\text{log}{}_2\left(x-3\right)\right)}^2+10\text{log}{}_2\left(x-3\right)-16=0.}\end{array}}$ Ez $\text{log}{}_2\left(x-3\right)$-ben másodfokú egyenlet, így a gyökképlet alapján $\begin{array}{c}{\displaystyle \text{log}{}_2\left(x-3\right)=\frac{-10\pm \sqrt[]{100+64}}{2}=-5\pm \sqrt[]{41}\mathrm{.}}\end{array}$ Ebből $x=3+2^{-5\pm \sqrt[]{41}}$. Ezért az eredeti egyenlet megoldásai: $\begin{array}{c}{\displaystyle x_1=3+2^{-5+\sqrt[]{41}}\approx 5\mathrm{,}6447\text{és}{x}_2=3+2^{-5-\sqrt[]{41}}\approx 3\mathrm{,}00037.}\end{array}$   2. Egy háromszög oldalhosszai olyan számtani sorozat első három eleme, amelynek második eleme $6$. $a)$ Adjuk meg azt a számhalmazt (a legegyszerűbb alakú) pontos értékekkel, amelynek elemei az ilyen háromszögek területei.  (7 pont) $b)$ Van-e az ilyen háromszögek között maximális területű, van-e minimális területű? Ha igen, akkor melyik az?  (2 pont) $c)$ Van-e az ilyen háromszögek között két olyan, amelyeknél a beírt kör sugara egyenlő? Ha igen, akkor melyek azok?  (3 pont)   Megoldás. $a)$ A számtani sorozat differenciájának abszolút értékét $d$-vel jelöljük, így az oldalhosszak $6-d$, 6 és $6+d$, ahol nyilván $0\le d$, és a háromszög-egyenlőtlenség miatt $6+d<6-d+6$, azaz $d<3$. A háromszög területét a Héron-képlettel számoljuk ki. A félkerület: $\begin{array}{c}{\displaystyle s=\frac{6-d+6+6+d}{2}=9.}\end{array}$ A terület: $\begin{array}{c}{\displaystyle T=\sqrt[]{9\left(9-\left(6-d\right)\right)\left(9-6\right)\left(9-\left(6+d\right)\right)}=\sqrt[]{27\left(9-d^2\right)}\mathrm{.}}\end{array}$ Ebből $0\le d<3$ miatt következik, hogy $0<T\le \sqrt[]{27\cdot 9}=9\sqrt[]{3}$, és $T$ minden ilyen értéket felvesz, így a keresett számhalmaz $\left]0;9\sqrt[]{3}\right]$. $b)$ Az $a)$ megoldásából következik, hogy ilyen háromszögek között minimális területű nincs, maximális területű van, a $d=0$ esetben. Ez a 6 oldalhosszúságú szabályos háromszög. $c)$ Ismeretes, hogy a háromszög beírt körének sugara $\varrho =\frac{T}{s}$. A feladatban szereplő háromszögeknél $s=9$ állandó, így $\varrho$ és $T$ kapcsolata kölcsönös és egyértelmű, tehát $\varrho$ és $d$ kapcsolata is az. Ezért a feladatban szereplő háromszögeknél a különböző háromszögek beírt körének sugara is különbözik. Tehát nincs két olyan háromszög, amelyeknél a beírt kör sugara egyenlő.   3. Egy ügyfél egy bankból $1980$-ban felvett egymillió Ft kölcsönt, évi $5\%$-os kamatra, $20$ évi, évente egyszeri, azonos összegű törlesztési kötelezettséggel. $a)$ Mennyi volt az évi törlesztési összeg, $10$ Ft-ra kerekítve?  (5 pont) A kölcsönszerződést nem lehetett megváltoztatni a növekvő infláció ellenére sem, pedig $1992$-ben $(12$ évvel a tárgyalt hitelfelvétel után$)$ már a bank adott $10\%$-os kamatot a nála elhelyezett pénzre. Ezért a bank a fent leírt kölcsön felvevőjének felajánlotta, hogy hátralevő tartozását megszüntetheti, ha az éppen fennálló tartozásának $90\%$-át kifizeti. $b)$ Mennyivel tartozott az ügyfél $12$ év leteltével?  (4 pont) $c)$ Mennyit helyezzen el az ügyfél egy (másik) bankban, hogy abból az eredeti törlesztő részletét évente kivéve és $10\%$-os kamattal számolva $8$ év alatt megszüntesse a tartozását? Érdemes-e elfogadni a bank ajánlatát, vagy kisebb összegnek egy (másik) bankban való elhelyezésével érdemes tovább törleszteni a tartozását?  (4 pont)   Megoldás. $a)$ A feladatban leírt kölcsöntörlesztésre $T$ kölcsön, $n$ évre, $p\%$-os kamat és $t$ törlesztőrészlet esetén, $q=1+\frac{p}{100}$ jelöléssel az ismert képlet érvényes: $\begin{array}{c}{\displaystyle T{q}^n=t\frac{q^n-1}{q-1}\mathrm{.}}\end{array}$ Ebből a mi esetünkben: $\begin{array}{c}{\displaystyle t=1000000\cdot \frac{1\mathrm{,}{05}^{20}\cdot 0\mathrm{,}05}{1\mathrm{,}{05}^{20}-1}\mathrm{.}}\end{array}$ Ezt zsebszámológéppel kiszámolva és azt tízesre kerekítve: $t\approx 80240$ Ft. $b)$ A járadékszámítási képletet használva és hasonlóan kiszámolva a 12 év után fennálló tartozás: $\begin{array}{c}{\displaystyle 1000000\cdot 1\mathrm{,}{05}^{12}-t\cdot \frac{1\mathrm{,}{05}^{12}-1}{0\mathrm{,}05}\approx 518660\text{Ft. }}\end{array}$ $c)$ Egy bankban elhelyezett $x$ összegből a fenti $t$ évjáradékot kivéve 8 év alatt évi 10% kamat mellett megszűnik az adósság. Az $x$ lép a képletben $T$ helyébe: $x\cdot 1\mathrm{,}{1}^8-t\frac{1\mathrm{,}{1}^8-1}{0\mathrm{,}1}$. Ebből $\begin{array}{c}{\displaystyle x=t\cdot \frac{1\mathrm{,}{1}^8-1}{0\mathrm{,}1\cdot 1\mathrm{,}{1}^8}\approx 428070\text{Ft}\mathrm{.}}\end{array}$ Mivel az 518 660 Ft összeg 90%-a 10 Ft-ra kerekítve $466790\text{Ft}>428070\text{Ft}$, érdemes folytatni a fenti módon a törlesztést.   4. Jelölje $k$ azt a kört, amelyik érinti a koordináta-rendszer $x$ tengelyét, és érinti az $f\left(x\right)=\frac{1}{3}\left(x^2+20\right)$ $\left(x\in \text{R}\right)$ függvény grafikonját a függvénynek a $2$ abszcisszájú pontjában. (A függvény grafikonjának az érintése egy pontban azt jelenti, hogy az érintő kör ebben a pontban érinti a grafikonhoz az adott pontban húzott érintőt, és az érintő elválasztja a grafikont és a kört.) $a)$ Írjuk fel a $k$ kör egyenletét.  (7 pont) $b)$ Mennyi annak a korlátos síkidomnak a területe, amelyet az $y$ tengely, az $x$ tengely, a $k$ kör és a függvény grafikonja határol?  (7 pont) 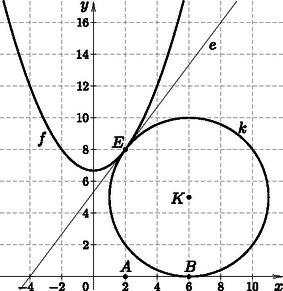  Megoldás. $a)$ A függvény 2 abszcisszájú pontja $E\left(2;8\right)$, a függvény grafikonjához ebben a pontban húzott érintő iránytangense $f\text{'}\left(2\right)=\frac{4}{3}$. A $k$ kör középpontja azon az egyenesen van, amely áthalad a $E\left(2;8\right)$ ponton és egy normálvektora $\overrightarrow{n}\left(3;4\right)$, ezért az egyenes egyenlete $3x+4y=38$.     A $k$ kör $K\left(u;v\right)$ középpontja rajta van az egyenesen, ezért $3u+4v=38$, másrészt ugyanolyan távol van $E$-től, mint az $x$ tengelytől, így $\begin{array}{c}{\displaystyle \sqrt[]{{\left(u-2\right)}^2+{\left(v-8\right)}^2}=v\mathrm{,}}\end{array}$ és erre ${\left(u-2\right)}^2+{\left(v-8\right)}^2=v^2$ is teljesül, de a feladat szerint nyilván csak $u>2$ és $0<v<8$ lehet, mert a kör az érintőnek a függvény grafikonjával ellentétes oldalán és az $x$ tengely felett van. A $3u+4v=38$, ${\left(u-2\right)}^2+{\left(v-8\right)}^2=v^2$ egyenletrendszert oldjuk meg. Mivel $3\left(u-2\right)=32-4v$, így ${\left(32-4v\right)}^2+9{\left(v-8\right)}^2=9v^2$. Ebből $25{\left(8-v\right)}^2=9v^2$, és az $u$-ra, $v$-re tett feltételek miatt $v=5$ és $u=6$. A kör egyenlete ${\left(x-6\right)}^2+{\left(y-5\right)}^2=25$. $b)$ A keresett terület kiszámításához felhasználjuk a függvénynek a $\left[0;2\right]$ intervallumon vett görbe alatti $t_1$ területét, az $A\left(2;0\right)E\left(2;8\right)K\left(6;5\right)B\left(6;0\right)$ trapéz $t_2$ területét, és az $EKB$ körcikk $t_3$ területét. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t_1}& {\displaystyle ={\int }_0^{2}f\left(x\right)\text{d}x={\left[\frac{x^3}{9}+\frac{20x}{3}\right]}_0^2=\frac{128}{9}\mathrm{,}}\hfill \\ \hfill {\displaystyle t_2}& {\displaystyle =\frac{AE+BK}{2}\cdot AB=\frac{8+5}{2}\cdot 4=\mathrm{26,}}\hfill \\ \hfill {\displaystyle t_3}& {\displaystyle =5^2\pi \cdot \frac{\alpha }{2\pi }=12\mathrm{,}5\cdot \alpha \mathrm{,}\text{ahol}\alpha =EKB\sphericalangle \mathrm{.}}\hfill \end{array}}$ Az $EKB$ háromszögben a koszinusz-tételt alkalmazva: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{E{K}^2+K{B}^2-E{B}^2}{2EK\cdot KB}=\frac{25+25-\left(64+16\right)}{2\cdot 5\cdot 5}=-0\mathrm{,}\mathrm{6,}}\end{array}$ így $t_3$ értéke zsebszámológéppel számolva és 3 tizedesre kerekítve 27,679. A keresett terület: $\begin{array}{c}{\displaystyle t=t_1+t_2-t_3=\frac{128}{9}+26-12\mathrm{,}5\cdot \alpha \approx 12\mathrm{,}54.}\end{array}$   II. rész     5. $a)$ Oldjuk meg az $X$ halmazra az $A\setminus X=B$; $A\cup X=C$ egyenletrendszert, ahol az adott $A$, $B$, $C$ halmazokra $B\subset A\subset C$ teljesül.  (6 pont) $b)$ Igazoljuk, hogy az $A$ és $B$ ítéletekre az $\left(A\vee B\right)^\left(A\vee \neg B\right)$ és $A$ ítéletek ekvivalensek.  (6 pont) $c)$ Igaz-e, hogy $\forall H\subset {\text{R}}^{+}$ és $\forall h\in H$ esetén $\exists n\in {\text{N}}^{+}$ úgy, hogy $\frac{1}{n}<h<n$? Ha nem, akkor adjunk rá példát, ha igen, akkor írjuk le, hogy az ilyen $n$ függ-e a $h$-tól, vagy nem? Állításunkat bizonyítani nem kell.  (4 pont)   Megoldás. $a)$ Mivel tetszőleges $A$ és $X$ halmazra nyilvánvaló (a műveletek definíciójából következően), hogy $X=\left(A\cup X\right)\setminus \left(A\setminus X\right)$, ezért $X=C\setminus B$. $b)$ Az $\left(A;B\right)$ ítéletpár lehetséges $\left(\text{i};\text{i}\right)$, $\left(\text{i};\text{h}\right)$, $\left(\text{h};\text{i}\right)$, $\left(\text{h};\text{h}\right)$ értékeit az $\left(A\vee B\right)^\left(A\vee \neg B\right)$ ítéletre kipróbálva rendre az i, i, h, h értéket kapjuk, ami az $A$ értéke, tehát valóban ekvivalensek. $c)$ Igaz, és az $n$ függ a $h$-tól.   6. $a)$ Hány olyan $2018$ pontú, páronként nem izomorf fagráf van, amelyekben nincs háromnál több élt tartalmazó út?  (11 pont) $b)$ Hol helyezkednek el a koordináta-rendszerben azoknak a $2018$ pontú fagráfoknak a pontjai, amelyek mindegyikének pontja az origó, és minden élének a két végpontja olyan $\left(x_1;y_1\right)$, $\left(x_2;y_2\right)$ pont, amelyre $x_1$, $y_1$, $x_2$, $y_2$ egész számok, és az $\left(x_1-x_2\right)$, $\left(y_1-y_2\right)$ számoknak az egyike $0$, a másik $0$, $1$, vagy $-1$.  (5 pont)   Megoldás. $a)$ Ha egy 2018 pontú fagráfban nincs háromnál több élt tartalmazó út, akkor ‐ mivel a gráf összefüggő ‐ a leghosszabb út kettő vagy három élt tartalmaz benne. Ha a fagrában minden út legfeljebb két élt tartalmaz, akkor egy ilyen út legyen az $AB$, $BC$ élekből álló $ABC$ részgráf. Ez a részgráf a fagráf más ($A$, $B$, $C$ csúcsoktól különböző) $P$ csúcsához sem $A$-ból, sem $C$-ből induló, $B$-t nem tartalmazó úttal nem csatlakozhat, mert különben lenne a gráfban három élből álló út. Tehát $BP$ út van a fagráfban, de ez csak a $BP$ él lehet, mert különben $A$-t $P$-vel két élnél hosszabb út kötné össze. Ezért (izomorfiától eltekintve) csak egy olyan 2018 pontú fagráf van, amelyben nincs kettőnél több élt tartalmazó út. Ha egy 2018 pontú fagráfban minden út legfeljebb három élből áll, és van három élből álló út, akkor legyen egy ilyen az $AB$, $BC$, $CD$ élekből álló út. A fentihez hasonlóan belátható, hogy egyrészt sem $A$-hoz, sem $D$-hez nem csatlakozhat a gráf további éle, mert különben lenne három élnél hosszabb út; másrészt a gráf minden további pontját a $B$ és $C$ pont közül pontosan az egyikkel él köti össze, mert különben lenne három élnél hosszabb út (vagy egy kör). Tehát, ha egy 2018 pontú fagráfban minden út legfeljebb három élből áll, és van három élből álló út, akkor a gráfnak az $AB$, $BC$, $CD$ éleken kívül $n$ darab ($0\le n\le 2014$) $B$-hez csatlakozó olyan éle, és $\left(2014-n\right)$ darab $C$-hez csatlakozó olyan éle van, amelynek másik végpontja nincs $A$, $B$, $C$, $D$ között. Rögzített $n$ esetén az $n$-hez és a $\left(2014-n\right)$- hez tartozó két gráf izomorf (illetve $n=1007$-nél azonos), tehát 1008 különböző ilyen fagráf van. Így a keresett szám 1009. $b)$ A feladatban leírt fagráfnak az origót a gráf tetszőleges $P\left(x;y\right)$ pontjával összekötő út éleinek száma nem kisebb, mint $|x|+|y|$, így $|x|+|y|\le 2017$. Ezért $P$ benne van az $N=\left(2017;0\right)$, $\left(0;2017\right)$, $\left(-2017;0\right)$, $\left(0;-2017\right)$ négyzetben, annak a határát is beleszámítva. Mivel $N$ minden pontja nyilván valamelyik fagráfnak pontja, ezért a fagráfok pontjai az $N$ négyzet belsejében vagy határán elhelyezkedő pontok.   7. Egy társaság $5$ nőből és $5$ férfiből áll, és köztük két házaspár van. $a)$ Hányféleképpen ülhetnek le egy kerek asztal köré, ha minden nő mindkét oldalán férfi ül? Két leülés különböző, ha van olyan személy a társaságban akinek a két leülésnél legalább az egyik oldal (jobb vagy bal) felől nem ugyanaz ül, mint a másik leülésnél.  (4 pont) $b)$ Hányféleképpen ülhetnek le egy kerek asztal köré, ha minden nő mindkét oldalán férfi ül, és mindkét férj a felesége jobb oldalán ül (két leülés különböző olyan módon, mint az $a)$ esetnél).  (4 pont) $c)$ Mennyi annak a valószínűsége, hogy a társaság úgy ül le, hogy minden nő mindkét oldalán férfi ül, de egyik férfi sem ül a felesége mellett?  (8 pont)   Megoldás. $a)$ Mivel ugyanannyi férfi van, mint nő, és két nő nem ül egymás mellett, ezért nők és férfiak felváltva ülnek. A nők ciklikus permutációban $4!=24$-féleképpen ülhetnek le. A nők leülése után a férfiak leülésének ciklikus cseréje már változást jelentene a leülésben, ezért az ő leülésük száma $5!=120$. Így a tejes leülési szám a kettő szorzata: $24\cdot 120=2880$. $b)$ A nők ciklikus permutációban $4!=24$-féleképpen ülhetnek le. Ezeknél a leüléseknél a két férj helye rögzített, a további három férfi pedig $3!=6$-féleképpen ülhet le. Tehát a keresett szám $24\cdot 6=144$. $c)$ A jobb leírás érdekében megjelöljük a székeket, nagybetűvel a nők, kis betűvel a férfiak székét, az óramutató járása szerint: $AaBbCcDdEe$. Az egyik (mindegy, hogy melyik) férjes nő ($n_1$) helyét rögzítjük, legyen ez $A$. A másik férjes nő ($n_2$) 4 különböző helyre ülhet. Ha $B$-re ült, akkor az $n_1$ nő $f_1$ férje 3 helyre: $b$, $c$, illetve $d$ székekre ülhetett, és ekkor $f_2$ férj rendre a $\left(c\mathrm{,}d\mathrm{,}e\right)$, a $\left(d\mathrm{,}e\right)$, illetve a $\left(c\mathrm{,}e\right)$ székekre ülhetett. Ez 7 eset. Ha $n_2$ $C$-re ült, akkor $f_1$ ugyanazokra a $b$, $c$, illetve $d$ székekre ülhetett, és ekkor $f_2$ férj rendre az $\left(a\mathrm{,}d\mathrm{,}e\right)$, az $\left(a\mathrm{,}d\mathrm{,}e\right)$, illetve az $\left(a\mathrm{,}e\right)$ székekre ülhetett. Ez 8 eset. A szimmetria miatt, ha $n_2$ nem $B$-re, hanem $E$-re, illetve nem $C$-re, hanem $D$-re ült, akkor is a férjek leülésére 7, illetve 8 lehetőség van. Tehát a házastársak leülésére 30 lehetőség van. Mindegyiknél $3!=6$ lehetőség a többi férfi leülésére, és $3!=6$ lehetőség a többi nő leülésére. Tehát, ha a társaság úgy ül le, hogy minden nő mindkét oldalán férfi ül, de egyik férfi sem ül a felesége mellett, akkor a lehetséges leülések száma $30\cdot 6\cdot 6=1080$. Az összes leülések száma az $a)$ rész szerint 2880, tehát a keresett valószínűség $\frac{1080}{2880}=\frac{3}{8}$.   8. Legyen $\begin{array}{c}{\displaystyle f\left(x\right)=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}2x\mathrm{,}}& {\displaystyle \text{ha }0\le x\le \pi \mathrm{,}}\hfill \\ \hfill {\displaystyle |2\text{sin}\left(x-\pi \right)|\mathrm{,}}& {\displaystyle \text{ha }\pi \le x\le 3\pi \mathrm{.}}\hfill \end{array}}}\end{array}$ $a)$ Differenciálható-e a függvény az $x_0=\pi$ pontban?  (4 pont) $b)$ Adjuk meg azt a legbővebb halmazt, amelyen a függvény szigorúan monoton növekvő, és amelyen szigorúan monoton csökkenő.  (6 pont) $c)$ Adjuk meg bizonyítás nélkül a függvény szélsőértékeinek helyét és értékét, de jelezzük nem csak azt, hogy minimum vagy maximum, hanem a szélsőértéknek a szigorú, a helyi és az abszolút tulajdonságát is.  (6 pont)   Megoldás. $a)$ Ha egy $g\left(x\right)$, $x\in \left(a;b\right)$ függvény differenciálható az $x_0\in \left(a;b\right)$ pontban, akkor a differenciálhányados definíciója szerint nyilvánvaló, hogy a $g\left(x\right)$, $x\in \left(a;x_0\right]$ függvény is és a $g\left(x\right)$, $x\in \left[x_0;b\right)$ függvény is differenciálható $x_0$-ban, és a differencálhányadosok egyenlők. Ennek alapján az $f\left(x\right)=\text{sin}2x$, ha $0\le x\le \pi$ függvény differenciálhányadosa $\pi$-ben $2\text{cos}2\pi =2$, és az $f\left(x\right)=|2\text{sin}\left(x-\pi \right)|$, ha $\pi \le x\le 3\pi$ függvény differenciálhányadosa $\pi$-ben $2\text{cos}0=2$. Másrészt az $f\left(x\right)=\text{sin}2x$, ha $0\le x\le \pi$ függvény differenciálhányadosa $\pi$-ben 2 és az $f\left(x\right)=|2\text{sin}\left(x-\pi \right)|$, ha $\pi \le x\le 3\pi$ függvény differenciálhányadosa $\pi$-ben 2 miatt az $\begin{array}{c}{\displaystyle f\left(x\right)=\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{sin}2x\mathrm{,}}& {\displaystyle \text{ha }0\le x\le \pi \mathrm{,}}\hfill \\ \hfill {\displaystyle |2\text{sin}\left(x-\pi \right)|\mathrm{,}}& {\displaystyle \text{ha }\pi \le x\le 3\pi \mathrm{.}}\hfill \end{array}}}\end{array}$ függvény is differenciálható $\pi$-ben (és a differenciálhányadosa 2). A bizonyítás tehát arra a tételre való hivatkozással történik, hogy egy függvény az értelmezési tartományának belső pontjában akkor és csak akkor differenciálható, ha abban a pontban van jobb és bal oldali differenciálhányadosa, és azok megegyeznek. $b)$ A függvény a $\left[0;\frac{1}{4}\pi \right]$, $\left[\frac{3}{4}\pi ;\frac{3}{2}\pi \right]$, $\left[2\pi ;\frac{5}{2}\pi \right]$ intervallumokon szigorúan monoton növekvő, mert a végpontok kivételével a differenciálhányadosok pozitívok: $\left(0;\frac{1}{4}\pi \right)$-ben $2\text{cos}2x>0$, $\left(\frac{3}{4}\pi ;\frac{3}{2}\pi \right)$-ben megosztva: $\left(\frac{3}{4}\pi ;\pi \right]$-ben $2\text{cos}2x>0$, $\left[\pi ;\frac{3}{2}\pi \right)$-ben $2\text{cos}\left(x-\pi \right)>0$, és $\left(2\pi ;\frac{5}{2}\pi \right)$-ben $|2\text{cos}\left(x-\pi \right)|>0$. De a zárt intervallumokon is érvényes a szigorú monotonitás, a definíció alapján bizonyítható. Ugyanis az intervallum kezdőpontjában felvett függvényérték kisebb, a végpontjában felvett függvényérték pedig nagyobb, mint a nyilt intervallumban felvett függvényérték. Hasonlóan bizonyítható, hogy az $\left[\frac{1}{4}\pi ;\frac{3}{4}\pi \right]$, $\left[\frac{3}{2}\pi ;2\pi \right]$, $\left[\frac{5}{2}\pi ;3\pi \right]$ zárt intervallumokon az $f\left(x\right)$ függvény szigorúan monoton csökkenő: az intervallumok belsejében a differenciálhányados negatív, a végpontokra a szigorú monotonitás a definíció alapján belátható. $c)$ A szélsőértékek helye és értéke: $x=0$-ban szigorú helyi minimum van, értéke 0. $x=\frac{1}{4}\pi$-ben szigorú helyi maximum van, értéke 1. $x=\frac{3}{4}\pi$-ben szigorú abszolút minimum van, értéke $-1$. $x=\frac{3}{2}\pi$-ben szigorú helyi és abszolut (nem szigorú) maximum van, értéke 2. $x=2\pi$-ben szigorú helyi minimum van, értéke 0. $x=\frac{5}{2}\pi$-ben szigorú helyi és abszolút (nem szigorú) maximum van, értéke 2. $x=3\pi$-ben szigorú helyi minimum van, értéke 0.   9. Egy könyvesboltban három kiadónak $($jelölésük legyen A, B, C) mind a négy középiskolai évfolyam részére szóló matematika tankönyve megtalálható, áruk az évfolyamtól nem, csak a kiadótól függően rendre 1500 Ft, 1800 Ft és 2000 Ft. A könyvekről a boltban levő példányok számára vonatkozóan az alábbi adatok állnak rendelkezésünkre. ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>9</mn></math>. évfolyamos:}}\hfill & {\displaystyle \text{<span style="font-weight: normal;font-style: normal;">A</span>-ból <span style="font-weight: normal;font-style: normal;">102 db,</span> <span style="font-weight: normal;font-style: normal;">B</span>-ből <span style="font-weight: normal;font-style: normal;">120 db,</span> <span style="font-weight: normal;font-style: normal;">C</span>-ből <span style="font-weight: normal;font-style: normal;">78 db</span> van;}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>10</mn></math>. évfolyamos:}}\hfill & {\displaystyle \text{összesen <span style="font-weight: normal;font-style: normal;">220 db</span> van, áruk átlagosan <span style="font-weight: normal;font-style: normal;">1750 Ft;</span>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>11</mn></math>. évfolyamos:}}\hfill & {\displaystyle \text{összesen <span style="font-weight: normal;font-style: normal;">210 db</span> van, áruk átlagosan <span style="font-weight: normal;font-style: normal;">1760 Ft;</span>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>12</mn></math>. évfolyamosról:}}\hfill & {\displaystyle \text{nincs adat, }}\hfill \end{array}}$ de tudjuk, hogy a négy évfolyaméból együtt (tehát az összes könyv) 810 db van, áruk átlagosan 1760 Ft. (Az átlagok egészre kerekített értékek). $a)$ Mennyi a raktáron levő $9$. évfolyamos könyvárak módusza, mediánja, átlaga és szórása?  (6 pont) $b)$ Mit tudunk a fenti adatok alapján a $12$. évfolyamos könyvek számáról és átlagáráról?  (5 pont) $c)$ Ha az A kiadó raktárban levő könyveinek a száma $305$, akkor mennyi a B és a C kiadók raktárban levő könyveinek száma, egészre kerekítve (az átlagok is egészre kerekített értékek voltak)?  (5 pont)   Megoldás. $a)$ A 9. évfolyamos könyvárak módusza: 1800, mediánja: 1800. Átlaga: $\begin{array}{c}{\displaystyle \frac{102\cdot 1500+120\cdot 1800+78\cdot 2000}{102+120+78}=1750.}\end{array}$ Szórása: $\begin{array}{c}{\displaystyle \sqrt[]{\frac{102\cdot {\left(1500-1750\right)}^2+120\cdot {\left(1800-1750\right)}^2+78\cdot {\left(2000-1750\right)}^2}{102+120+78}}\mathrm{,}}\end{array}$ egészre kerekítve 196. $b)$ A 12. évfolyamos könyvek darabszámát az összesből a többi évfolyamos darabszámát levonva kapjuk, száma: $810-300-220-210=80$. Ha a 12. évfolyamos könyvek átlagára $x$ Ft, akkor az összes könyv árát kétféleképpen kiszámolva az $x$-re egyenletet kapunk: $\begin{array}{c}{\displaystyle 810\cdot 1760=300\cdot 1750+220\cdot 1750+210\cdot 1760+80x\mathrm{.}}\end{array}$ Ebből a 12. évfolyamos könyvek átlagára: $x=1825$ Ft. $c)$ Legyen a $B$, illetve a $C$ kiadók raktárban levő könyveinek száma $b$, illetve $c$. Tehát $b+c=810-305=505$, és az átlagáruk alapján $\begin{array}{c}{\displaystyle 1500\cdot 305+1800b+2000c=810\cdot \mathrm{1760,}\text{azaz}18b+20c=9681.}\end{array}$ A két egyenletből (egészre kerekítve): $b=220$ és $c=285$.