Cím:	Megoldásvázlatok a 2018/2. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Lorántfy László
Füzet:	2018/március, 142 - 152. oldal	PDF  |  MathML
Hivatkozás(ok):	2018/február: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Egy bolthálózat húszéves fennállása alkalmából azzal kedveskedik a vásárlóknak, hogy $20\%$ kedvezményt kapnak vásárlásuk összegéből, ha $4$ kockával dobva a dobott számok összege legalább $20$. $a)$ Mekkora ennek a valószínűsége? $b)$ Becsüljük meg, mennyibe kerül a vállalatnak ez az akció a jubileumi évben, ha $38000$ vásárlóra számítanak és a vásárlások összegszerű megoszlását az alábbi táblázatban adták meg: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cc|}\hline \hfill {\displaystyle \text{0 ‐ 4999 Ft}}& \hfill {\displaystyle \text{12\% }}\\ \hfill {\displaystyle \text{5000 ‐ 9999 Ft}}& \hfill {\displaystyle \text{36\% }}\\ \hfill {\displaystyle \text{10 000 ‐ 14 999 Ft}}& \hfill {\displaystyle \text{47\% }}\\ \hfill {\displaystyle \text{15 000 ‐ 50 000 Ft }}& \hfill {\displaystyle \text{5\% }}\\ \hline\end{array}}}\end{array}$  (11 pont)   Megoldás. $a)$ Az összes esetek száma: $N_{\text{ö}}=6^4=1296$. Kedvező esetek:   ${\displaystyle \begin{array}{|cc|}\hline {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>24</mn></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">=</mo><mn>20</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mo>⋅</mo><mn>1</mn><mo stretchy="false">=</mo><mn>2</mn></math> eset}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>23</mn></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>22</mn></math>,}}\hfill & {\displaystyle }\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>21</mn></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>20</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo>⋅</mo><mrow><mo>(</mo><mfrac linethickness="0"><mrow><mn>4</mn></mrow><mrow><mn>1</mn></mrow></mfrac><mo>)</mo></mrow><mo stretchy="false">=</mo><mn>5</mn><mo>⋅</mo><mn>4</mn><mo stretchy="false">=</mo><mn>20</mn></math> eset }}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>21</mn></math>}}\hfill & {\displaystyle }\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>22</mn></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mo stretchy="false">+</mo><mn>4</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>20</mn></math> }}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mo>⋅</mo><mrow><mo>(</mo><mfrac linethickness="0"><mrow><mn>4</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>)</mo></mrow><mo stretchy="false">=</mo><mn>2</mn><mo>⋅</mo><mn>6</mn><mo stretchy="false">=</mo><mn>12</mn></math> eset <math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="12pt" depth="6pt"></mspace></mphantom></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>21</mn></math>, <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">=</mo><mn>20</mn></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo>⋅</mo><mrow><mo>(</mo><mfrac linethickness="0"><mrow><mn>4</mn></mrow><mrow><mn>2</mn></mrow></mfrac><mo>)</mo></mrow><mo>⋅</mo><mn>2</mn><mo stretchy="false">=</mo><mn>3</mn><mo>⋅</mo><mn>12</mn><mo stretchy="false">=</mo><mn>36</mn></math> eset <math xmlns="http://www.w3.org/1998/Math/MathML"><mphantom><mspace backround="\#000" height="12pt"></mspace></mphantom></math>}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>3</mn><mo stretchy="false">+</mo><mn>5</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">+</mo><mn>6</mn><mo stretchy="false">=</mo><mn>20</mn></math> }}\hfill & {\displaystyle }\hfill \\ \hline\end{array}}$ $\begin{array}{c}{\displaystyle N_{\text{k}}=70.}\end{array}$ A keresett valószínűség: $p=\frac{N_{\text{k}}}{N_{\text{ö}}}=\frac{70}{1296}\approx 0\mathrm{,}054$. $b)$ A várható 38 000 vásárló közül a kapott valószínűség szerint 2052 fog nyerni. A nyerteseket a vásárlások megoszlása szerint szétosztva, és a megadott összeghatárok középértékével számolva:   ${\displaystyle \begin{array}{|cccc|}\hline \hfill {\displaystyle \text{2 500 Ft}}& \hfill {\displaystyle \text{ 12\%}}& \hfill {\displaystyle \text{ 246}}& \hfill {\displaystyle \text{ 615 000 }}\\ \hfill {\displaystyle \text{7 500 Ft}}& \hfill {\displaystyle \text{ 36\%}}& \hfill {\displaystyle \text{ 739}}& \hfill {\displaystyle \text{ 5 542 500 }}\\ \hfill {\displaystyle \text{12 500 Ft}}& \hfill {\displaystyle \text{ 47\%}}& \hfill {\displaystyle \text{ 964}}& \hfill {\displaystyle \text{ 12 050 000 }}\\ \hfill {\displaystyle \text{32 500 Ft }}& \hfill {\displaystyle \text{ 5\%}}& \hfill {\displaystyle \text{ 103}}& \hfill {\displaystyle \text{ 3 347 500 }}\\ \hfill {\displaystyle \text{Összesen:}}& \hfill {\displaystyle \text{ 100\%}}& \hfill {\displaystyle \text{ 2,052 }}& \hfill {\displaystyle \text{ 21 555 000 }}\\ \hline\end{array}}$   Tehát várhatóan 21 555 000 Ft-ba fog kerülni a jubileumi akció a cégnek.   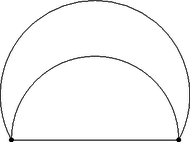2. Egy LED lámpát úgy alakítottak ki, hogy a LED fényforrásokat egy félgömb felületén helyezték el és azért, hogy a felülete ne legyen vakító, egy gömbszelet alakú opálos burát helyeztek fölé az ábrának megfelelően. A két bura falvastagsága elhanyagolható. A félgömb sugara 15 cm, a bura felülete pedig pont kétszerese a félgömb felszínének. A lámpákat a gyárban négyzetes oszlop alakú papírdobozokba csomagolják úgy, hogy a csillárok ne mozdulhassanak el a dobozban. Mekkorák legyenek a dobozok külső méretei, ha a rétegelt papír vastagsága $d=5$ mm?  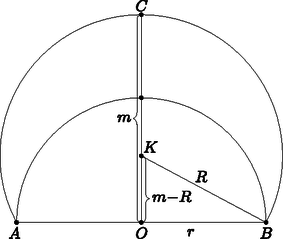(12 pont)       Megoldás. Használjuk az ábra jelöléseit. A félgömb középpontja legyen $O$, sugara $r=15$ cm, a gömbszelet középpontja $K$, sugara $R$, magassága $m$.     A félgömb felszíne: $A=2{\pi r}^2$, a bura felszíne: $A_B=2\pi Rm$. A feltétel szerint $A_B=2A$, vagyis $2\pi Rm=4{\pi r}^2$, amiből $Rm=2r^2$. A $BKO$ derékszögű háromszögben írjuk fel a Pitagorasz-tételt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(m-R\right)}^2+r^2}& {\displaystyle =R^2\mathrm{,}}\hfill \\ \hfill {\displaystyle m^2-2mR+R^2+r^2}& {\displaystyle =R^2\mathrm{,}}\hfill \\ \hfill {\displaystyle m^2}& {\displaystyle =2mR-r^2\mathrm{.}}\hfill \end{array}}$ Behelyettesítve $Rm$ értékét: $m^2=3r^2$. Mivel $m>0$, így $m=\sqrt[]{3}r\approx 25\mathrm{,}98$ cm és $\begin{array}{c}{\displaystyle R=\frac{2r^2}{m}=\frac{2r^2}{\sqrt[]{3}r}=\frac{2r}{\sqrt[]{3}}=17\mathrm{,}32\text{cm.}}\end{array}$ A doboz külső méretei: $a=2\left(R+d\right)\approx 35\mathrm{,}64$ cm és $m\approx 25\mathrm{,}98$ cm.   3. Egy személyautó fedélzeti számítógépe az átlagfogyasztást az előzőleg megtett 100 km alapján számítja. A tankban lévő üzemanyag mennyiségét is ismerve így azt is jelzi, hogy hány km-t tudunk még autózni a meglévő üzemanyaggal, nevezzük ezt hatótávolság. Egy alkalommal induláskor a hatótáv kijelzett értéke 500 km. Egyenletes sebességgel haladunk autópályán. 50 km megtétele után a kijelző 588 km-es hatótávot jelez. Ezután még 680 km-t teszünk meg ugyanezzel az egyenletes sebességgel, amikor az üzemanyag jelző vészvillogó kigyullad, jelezve, hogy már csak 5 l üzemanyagunk van. Mennyi üzemanyag volt a tankban induláskor?   Megoldás. Legyen a tankban lévő üzemanyag induláskor $x$ liter, az autópályán történő egyenletes haladáskor a fogyasztás $y$ liter/km. Mivel a hatótáv induláskor 500 km, így az előzőleg megtett 100 km-en $\frac{x}{500}$ liter/km volt az átlagfogyasztás. 50 km megtétele után a gépkocsi $50y$ liter üzemanyag fogyasztott, ezért a tankban most $x-50y$ liter benzin van. Az előző 100 km-en az átlagfogyasztás: $\begin{array}{c}{\displaystyle \frac{1}{2}\left(\frac{x}{500}+y\right)\mathrm{.}}\end{array}$ Ezzel a fogyasztással számolva a tankban lévő üzemanyag még 588 km-re lenne elegendő, így $\begin{array}{c}{\displaystyle \frac{588}{2}\left(\frac{x}{500}+y\right)=x-50y\mathrm{.}}\end{array}$ Indulástól a vészvillogó kigyulladásáig $50+680=730$ km-t tettünk meg $y$ liter/km átlagfogyasztással, vagyis $730y$ liter üzemanyagot fogyasztottunk el, ezért $x-730y=5$. A második egyenletből $x$-et kifejezve: $x=730y+5$. Ezt visszahelyettesítve az első egyenletbe és rendezve: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 294\left(\frac{730y+5}{500}+y\right)}& {\displaystyle =730y+5-50y\mathrm{,}}\hfill \\ \hfill {\displaystyle 723\mathrm{,}24y+2\mathrm{,}94}& {\displaystyle =680y+\mathrm{5,}}\hfill \\ \hfill {\displaystyle 43\mathrm{,}24y}& {\displaystyle =2\mathrm{,}\mathrm{06,}}\hfill \\ \hfill {\displaystyle y}& {\displaystyle \approx 0\mathrm{,}047641.}\hfill \end{array}}$ Ezt beírva a második egyenletbe: $x\approx 39\mathrm{,}78$. Tehát induláskor 39,78 liter üzemanyag volt a tankban.   4. Egy torony csonkakúp alakú kupolája alul 4 m, felül 3 m kerületű, alkotója pedig 2 m. A kupola egyik oldalán egy hangya mászik fel a torony tengelyének síkjában, 47 cm-re van a kupola alsó szegélyétől. A vele átellenes oldalon egy másik hangya mászik felfelé ugyanabban a síkban, és már csak 3 cm hiányzik, hogy elérje a kupola tetejét. Ekkor a két hangya az eredeti úti célt feladva, a lehető legrövidebb úton egymás felé indul. Mekkora távolságot tesznek meg a találkozásig, ha egyenlő sebességgel haladnak?  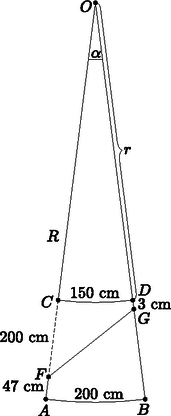(14 pont)   Megoldás. Egészítsük ki a csonkakúp palást felét körcikké. Használjuk az ábra jelöléseit.     Legyen $OA=OB=R$, $OC=OD=r$. Az első hangya helyét jelölje az $F$ pont, így $AF=47$ cm, a másodikét a $G$ pont, így $GD=3$ cm. $AC=BD=200$ cm, így $R=r+200$. Az adott kerület értékekből következik, hogy a körívek hossza: $AB=200$ cm, $CD=150$ cm. Az $OCD$ és $OAB$ körcikkek hasonlósága miatt: $\begin{array}{c}{\displaystyle \frac{R}{200}=\frac{r}{150}\mathrm{,}\text{vagyis}\frac{r+200}{200}=\frac{r}{150}\mathrm{,}}\end{array}$ amiből $r=600$ cm adódik. Számoljuk ki az $\alpha$ szöget: $\begin{array}{c}{\displaystyle \frac{\alpha }{{360}^{\circ }}=\frac{{CD}_{\text{ív}}}{2r\pi }\mathrm{,}\text{amiből}\alpha =\frac{150}{2\cdot 600\pi }\cdot {360}^{\circ }\approx 14\mathrm{,}{32}^{\circ }\mathrm{.}}\end{array}$ Az $OFG$ háromszögben keressük az $FG$ oldalt, $OF=r+CF=600+153=753$ cm, $OG=r+3=603$ cm. Használjuk a koszinusz-tételt: $\begin{array}{c}{\displaystyle {FG}^2={753}^2+{603}^2-2\cdot 753\cdot 603\cdot \text{cos}14\mathrm{,}{32}^{\circ }\mathrm{.}}\end{array}$ Ebből $FG\approx 225\mathrm{,}20$ cm. Mivel azonos sebességgel haladnak, ezért egy hangyának ennek a felét, $112\mathrm{,}62$ cm-t kell megtenni.   II. rész     5. 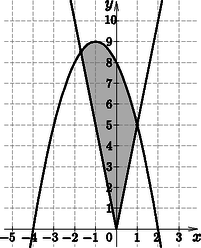$a)$ Oldjuk meg az alábbi egyenletet: $\begin{array}{c}{\displaystyle 5|x|=x\cdot (3x+2-2\sqrt[]{8-2x-x^2})\mathrm{.}}\end{array}$ $b)$ Határozzuk meg az $f\left(x\right)=-x^2-2x+8$ és a $g\left(x\right)=5|x|$ függvények által közrezárt területrész nagyságát.  (16 pont)   Megoldás. $x=0$ megoldása az egyenletnek, mert ekkor a gyökjel alatti kifejezés értéke pozitív és mindkét oldal $0$. Legyen $x>0$. Ekkor $\begin{array}{c}{\displaystyle 5x=x\cdot \left(3x+2-2\sqrt[]{8-2x-x^2}\right)\mathrm{.}}\end{array}$ A $-x^2-2x+8=0$ másodfokú egyenlet megoldásai $-4$ és $2$. Így $-x^2-2x+8\ge 0$ akkor teljesül, ha $0<x\le 2$. Ekkor mindkét oldalt osztva $x$-szel: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 5=3x+2-2\sqrt[]{-x^2-2x+8}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\sqrt[]{-x^2-2x+8}=3x-3.}\hfill \end{array}}$ Mindkét oldalt négyzetre emelve (ez $x\ge 1$ esetén ekvivalens átalakítás): $\begin{array}{c}{\displaystyle 4\left(-x^2-2x+8\right)=9x^2-18x+9.}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle 0=13x^2-10x-23.}\end{array}$ A másodfokú egyenlet gyökei: $x_1=\frac{23}{13}$ és $x_2=-1$. A kezdő feltétel és a kikötés miatt az egyenlet megoldása: $x_1=\frac{23}{13}$. Legyen $x<0$. Ekkor $\begin{array}{c}{\displaystyle -5x=x\cdot \left(3x+2-2\sqrt[]{8-2x-x^2}\right)\mathrm{.}}\end{array}$ A $-x^2-2x+8\ge 0$ egyenlőtlenség akkor teljesül, ha $-4\le x<0$. Mindkét oldalt osztva $x$-szel: ${\displaystyle \begin{array}{c}\hfill {\displaystyle -5=3x+2-2\sqrt[]{-x^2-2x+8}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\sqrt[]{-x^2-2x+8}=3x+7.}\hfill \end{array}}$ Mindkét oldalt négyzetre emelve (ez $x\ge -\frac{7}{3}$ esetén ekvivalens lépés): $\begin{array}{c}{\displaystyle 4\left(-x^2-2x+8\right)=9x^2+42x+49.}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle 0=13x^2+50x+17.}\end{array}$ A másodfokú egyenlet gyökei: $\begin{array}{c}{\displaystyle x_3=\frac{-25-2\sqrt[]{101}}{13}\approx -3\mathrm{,}4692\text{és}{x}_4=\frac{-25+2\sqrt[]{101}}{13}\approx -0\mathrm{,}3769.}\end{array}$ Mindkét megoldás megfelel a kikötéseknek. Összegezve: Négy megoldást találtunk. Ebből három kielégíti az egyenletet. $b)$ Határozzuk meg a metszéspontok $x$ koordinátáit.     $x\ge 0$ esetén $5x=-x^2-2x+8$, vagyis $\begin{array}{c}{\displaystyle x^2+7x-8=0.}\end{array}$ A pozitív megoldás $x_1=1$. $x<0$ esetén $-5x=-x^2-2x+8$, vagyis $\begin{array}{c}{\displaystyle x^2-3x-8=0.}\end{array}$ A negatív megoldás $x_2\approx -1\mathrm{,}7$. A közrezárt területrész nagysága: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =\underset{-1\mathrm{,}7}{\overset{0}{\int }}\left(-x^2-2x+8-\left(-5x\right)\right)\text{d}x+\underset{0}{\overset{1}{\int }}\left(-x^2-2x+8-5x\right)\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\underset{-1\mathrm{,}7}{\overset{0}{\int }}\left(-x^2+3x+8\right)\text{d}x+\underset{0}{\overset{1}{\int }}\left(-x^2-7x+8\right)\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left[-\frac{x^3}{3}+\frac{3x^2}{2}+8x\right]}_{-1\mathrm{,}7}^0+{\left[-\frac{x^3}{3}-\frac{7x^2}{2}+8x\right]}_0^1\approx 7\mathrm{,}63+4\mathrm{,}17=11\mathrm{,}8.}\hfill \end{array}}$   6. Egy üzemanyagtöltő állomás földalatti benzintároló tartálya egy fekvő hengerpalástból és a két végét lezáró két félgömbből áll. Teljes hossza 6 m, sugara 1,2 m. $a)$ Mekkora a tartály térfogata? $b)$ Mennyi benzin van benne, ha a szintmérő úszó éppen a sugár felénél áll? $c)$ Egy tartálykocsiból feltöltik a tárolót. Mennyi benzint engedtek bele, ha a szintmérő 92 cm-rel emelkedett?  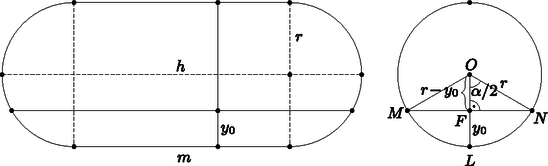(16 pont)   Megoldás. $a)$ Használjuk az ábra jelöléseit. $h=6$ m, $r=1\mathrm{,}2$ m. A tartály térfogata egy henger és egy gömb térfogatának az összege. A henger magassága $m=h-2r=3\mathrm{,}6$ m. $\begin{array}{c}{\displaystyle V=r^2\pi m+\frac{4r^3\pi }{3}={1\mathrm{,}2}^2\pi \cdot 3\mathrm{,}6+\frac{4\cdot {1\mathrm{,}2}^3\pi }{3}\approx 23\mathrm{,}524{\text{m}}^3\mathrm{.}}\end{array}$     $b)$ A szintmérő $y_0=\frac{r}{2}=0\mathrm{,}6$ m magasan áll. Az $OFN$ derékszögű háromszögben $\begin{array}{c}{\displaystyle \text{cos}\frac{\alpha }{2}=\frac{r-y_0}{r}=\frac{0\mathrm{,}6}{1\mathrm{,}2}=\frac{1}{2}\mathrm{,}\text{ezért}\frac{\alpha }{2}={60}^{\circ }\mathrm{,}\alpha ={120}^{\circ }=\frac{2\pi }{3}\text{rad}\mathrm{.}}\end{array}$ Az $LMN$ körszelet területe: $\begin{array}{c}{\displaystyle T_{\text{sz}}=\frac{1}{2}{r}^2\left({\alpha }_r-\text{sin}\alpha \right)=\frac{1}{2}1\mathrm{,}{2}^2\left(\frac{2\pi }{3}-\text{sin}{120}^{\circ }\right)\approx 0\mathrm{,}884426{\text{m}}^2\mathrm{.}}\end{array}$ Az üzemanyag térfogata egy gömbszelet és egy körszelet alapú hasáb térfogatának összege. A gömbszelet magassága $y_0$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_0}& {\displaystyle =V_{\text{gsz}}+V_{\text{h}}=\pi r{y}_0^2-\frac{\pi y_0^3}{3}+T_{sz}\cdot m\approx \pi \cdot 1\mathrm{,}2\cdot {0\mathrm{,}6}^2-\frac{\pi \cdot 0\mathrm{,}{6}^3}{3}+0\mathrm{,}884426\cdot 3\mathrm{,}\mathrm{6,}}\hfill \\ \hfill {\displaystyle V_0}& {\displaystyle \approx 4\mathrm{,}315{\text{m}}^3\mathrm{.}}\hfill \end{array}}$ Tehát $4\mathrm{,}315{\text{m}}^3$ benzin van a tartályban. 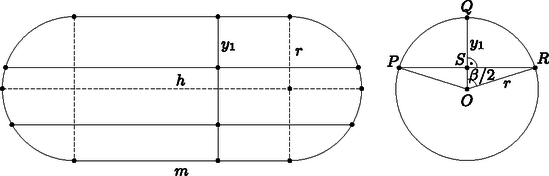$c)$ Ha a szintmérő $92$ cm-t emelkedik, akkor $0\mathrm{,}6+0\mathrm{,}92=1\mathrm{,}52$ m magasan fog állni, vagyis a tartály tetejéig még $y_1=\mathrm{2,4}-1\mathrm{,}52=0\mathrm{,}88$ m távolság van. Számítsuk ki a tartályban lévő levegő térfogatát a $b)$ pontban alkalmazott módszerrel és ebből már egyszerűen megkaphatjuk, mennyi benzint engedtek a tartályba.     Az $ORS$ derékszögű háromszögben $\begin{array}{c}{\displaystyle \text{cos}\frac{\beta }{2}=\frac{r-y_1}{r}=\frac{0\mathrm{,}32}{1\mathrm{,}2}=\frac{4}{15}\mathrm{,}\text{ezért}\frac{\alpha }{2}\approx 1\mathrm{,}30086\text{rad}\mathrm{,}\alpha \approx 2\mathrm{,}60173\text{rad}\mathrm{.}}\end{array}$ Az $LMN$ körszelet területe: $\begin{array}{c}{\displaystyle T_{\text{sz1}}=\frac{1}{2}{r}^2\left({\alpha }_r-\text{sin}{\alpha }_r\right)\approx \frac{1}{2}{1\mathrm{,}2}^2\left(2\mathrm{,}60173-\text{sin}2\mathrm{,}60173\right)\approx 1\mathrm{,}50315{\text{m}}^2\mathrm{.}}\end{array}$ A gömbszelet magassága $y_1$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_1}& {\displaystyle =V_{\text{gsz1}}+V_{\text{h1}}=\pi r{y}_1^2-\frac{\pi y_1^3}{3}+T_{\text{sz1}}\cdot m=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi \cdot 1\mathrm{,}2\cdot {0\mathrm{,}88}^2-\frac{\pi \cdot 0\mathrm{,}{88}^3}{3}+1\mathrm{,}50315\cdot 3\mathrm{,}6\approx 7\mathrm{,}61712{\text{m}}^3\mathrm{,}}\hfill \\ \hfill {\displaystyle V_1}& {\displaystyle \approx 7\mathrm{,}617{\text{m}}^3\mathrm{.}}\hfill \end{array}}$ A tartályba töltött benzin mennyisége: $\begin{array}{c}{\displaystyle V_{\text{BE}}=V-V_0-V_1=23\mathrm{,}524-4\mathrm{,}315-7\mathrm{,}617=11\mathrm{,}592{\text{m}}^3\mathrm{.}}\end{array}$   7. Egy ismeretlen alapú számrendszerben az ${\overline{ab}}_x$ kétjegyű szám és a számjegyei felcserélésével kapott ${\overline{ba}}_x$ kétjegyű szám között a következő összefüggések állnak fenn: $1.$ ${\overline{ab}}_x+{\overline{ba}}_x={\overline{110}}_x$, $2.$ ${\overline{ab}}_x-{\overline{ba}}_x={\overline{20}}_{10}$. $a)$ Határozzuk meg a számrendszer alapját. $b)$ Az ilyen alapú számrendszerekben milyen oszthatósági szabály érvényes a $3$-mal és az $5$-tel való oszthatóságra? $c)$ Határozzuk meg a $c$ és $d$ számjegyek értékét úgy, hogy az ${\overline{12c45d}}_x$ alakú szám a lehető legnagyobb $15$-tel osztható szám legyen ezekben a számrendszerekben.  (16 pont)   Megoldás. $a)$ Az első egyenletben az 1-es helyiértékű számjegyeket összeadva látszik, hogy $b+a=x$, vagyis $b=x-a$. A második egyenletből: $\begin{array}{c}{\displaystyle ax+b-bx-a=20.}\end{array}$ Ebbe beírva az első egyenletből kapott összefüggést: $\begin{array}{c}{\displaystyle ax+x-a-\left(x-a\right)\cdot x-a=20.}\end{array}$ Rendezve: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2ax-2a-x^2+x}& {\displaystyle =\mathrm{20,}}\hfill \\ \hfill {\displaystyle 2a\left(x-1\right)-x\left(x-1\right)}& {\displaystyle =\mathrm{20,}}\hfill \\ \hfill {\displaystyle \left(2a-x\right)\left(x-1\right)}& {\displaystyle =20.}\hfill \end{array}}$ Ha $x$ páros szám, akkor $\left(x-1\right)$ páratlan, $\left(2a-x\right)$ pedig páros. Ha $x$ páratlan szám, akkor $\left(x-1\right)$ páros és $\left(2a-x\right)$ páratlan. A két szorzótényező tehát ellenkező paritású. 20 osztóit figyelembe véve 4 esetet kell megvizsgálnunk: 1. $\left(2a-x\right)\left(x-1\right)=1\cdot 20$. Ekkor $x-1=20$, vagyis $x=21$, és $2a-x=1$, vagyis $a=11$. Ez megoldás. 2. $\left(2a-x\right)\left(x-1\right)=20\cdot 1$. Ekkor $x-1=1$, vagyis $x=2$, és $2a-x=20$, vagyis $a=11$. Mivel $a>x$, ezért ez nem megoldás. 3. $\left(2a-x\right)\left(x-1\right)=4\cdot 5$. Ekkor $x-1=5$, vagyis $x=6$, és $2a-x=4$, vagyis $a=5$. Ez megoldás. 4. $\left(2a-x\right)\left(x-1\right)=5\cdot 4$. Ekkor $x-1=4$, vagyis $x=5$, és $2a-x=5$, vagyis $a=5$. Mivel $a=x$, ezért ez nem megoldás. Tehát a számrendszer alapja $x=6$ vagy $x=21$ lehet. $b)$ Egy $6$ vagy $21$ alapú számrendszerben pontosan akkor osztható 3-mal egy szám, ha az utolsó számjegye osztható, hiszen a számrendszer alapja osztható 3-mal. Mivel $6=5+1$ és $21=4\cdot 5+1$, ezért a 6 és 21 minden hatványa 5-tel osztva 1-et ad maradékul. Így ezekben a számrendszerekben egy szám akkor osztható 5-tel, ha számjegyeinek összege osztható 5-tel. $c)$ Legyen $x=6$. Ekkor az ${\overline{12c45d}}_6$ akkor lesz 15-tel osztható, ha 3-mal és 5-tel is osztható. 3-mal akkor osztható, ha utolsó számjegye $d=0$ vagy $d=3$. ${\overline{12c450}}_6$ esetén a számjegyek összege $12+c$. Ez csak $c=3$ esetén lesz 5-tel osztható, így a szám ${\overline{123450}}_6$. ${\overline{12c453}}_6$ esetén a számjegyek összege $15+c$. Ez csak $c=5$ esetén lesz 5-tel osztható. Ekkor a szám ${\overline{125453}}_6$. Ez a nagyobb szám. Legyen $x=21$. Ekkor az ${\overline{12c45d}}_{21}$ utolsó számjegye lehet $18$. Ekkor a számjegyek összege $30+c$. Az 5-tel való oszthatósághoz lehet $c=20$. Ez a legnagyobb számjegy a $21$-es számrendszerben, így biztosan ez a feltételeknek megfelelő legnagyobb szám, tehát $\begin{array}{c}{\displaystyle {\overline{12\left(20\right)45\left(18\right)}}_{21}\mathrm{.}}\end{array}$   8. Péter egy 5,2 millió Ft értékű új autót vásárol egy autókereskedőtől. Az összeg $40\%$-a az önrész, amit átvételkor ki kell fizetnie, az ár fennmaradó részét $5$ év alatt törleszti, évi egyenlő részletekben $8\%$-os éves kamattal. $a)$ Mennyi lesz Péter éves törlesztő részlete? A kereskedő ajánlata, hogy ha $5$ év múlva egy ugyanilyen értékű kocsit vesz nála, akkor ezt az autót visszavásárolja tőle, évi $10\%$ értékcsökkenést figyelembe véve és csak az árkülönbözetet kell kifizetnie. $b)$ Mennyit kell fizetnie Péternek az új autóért $5$ év múlva, ha elfogadja az ajánlatot? Péter elhatározza, hogy elfogadja a kereskedő ajánlatát és előtakarékoskodik az $5$ év múlva esedékes autócserére. A bank legjobb ajánlata évi $2\mathrm{,}4\%$-os kamat $5$ éves futamidőre havi egyenlő részletekben történő befizetéssel, havi kamatozással. (A havi kamat az éves kamat tizenketted része.) Mekkora összeget fizessen be a bankba havonta, hogy az $5$ év után kivett összegből fedezni tudja az autó cseréjét?  (16 pont)   Megoldás. $a)$ Az $5200\cdot 0\mathrm{,}6=3120$ eFt hitelt 8% kamattal évi $x$ eFt-os egyenlő részletekben 5 év alatt törleszti úgy, hogy az utolsó befizetéskor a hitel lejár. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3120\cdot {1\mathrm{,}08}^5}& {\displaystyle =x\cdot {1\mathrm{,}08}^4+x\cdot {1\mathrm{,}08}^3+x\cdot {1\mathrm{,}08}^2+x\cdot {1\mathrm{,}08}^1+x\mathrm{,}}\hfill \\ \hfill {\displaystyle 4584\mathrm{,}3036}& {\displaystyle =x\cdot \frac{{1\mathrm{,}08}^5-1}{1\mathrm{,}08-1}=5\mathrm{,}8666x\mathrm{,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle \approx 781\mathrm{,}424\text{eFt}\mathrm{.}}\hfill \end{array}}$ Az éves törlesztő részlet 781 424 Ft lesz. $b)$ 5 év múlva a 10% értékcsökkenést figyelembe véve az autó értéke $5200000\cdot {0\mathrm{,}9}^5\approx 3070548$ eFt lesz, ezért Péternek $5200000-3070548=2129452$ eFt-ot kell fizetni 5 év múlva a kereskedőnek a cseréért. $c)$ 5 év alatt, havi $x$ Ft-os befizetéssel, évi 2,4%-os, vagyis havi 0,2%-os kamattal 2 129 452 Ft-ot kell összegyűjtenie. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x\cdot {1\mathrm{,}002}^{60}+x\cdot {1\mathrm{,}002}^{59}+\text{...}+x\cdot {1\mathrm{,}002}^2+x\cdot 1\mathrm{,}002}& {\displaystyle =2129\mathrm{452,}}\hfill \\ \hfill {\displaystyle 1\mathrm{,}002\cdot x\cdot \frac{{1\mathrm{,}002}^{60}-1}{1\mathrm{,}002-1}}& {\displaystyle =2129\mathrm{452,}}\hfill \\ \hfill {\displaystyle x}& {\displaystyle \approx 33373\text{Ft}\mathrm{.}}\hfill \end{array}}$ Tehát 33 373 Ft-ot kell havonta befizetnie, hogy 5 év múlva a kivett összegből fedezni tudja az autó cseréjét.   9. Egy $12$ pontú egyszerű gráfnak $56$ éle van. $a)$ Legalább hány kilencnél nagyobb fokszámú csúcsa van a gráfnak? $b)$ Bizonyítsuk be, hogy a gráf összefüggő. Egy asztalitenisz csapatnak $6$ férfi és $6$ nő versenyzője van. $c)$ Az edzőnek két férfi, két női és két vegyes párost kell kiválasztania egy közelgő versenyre. Egy versenyző legfeljebb két különböző típusú párosban játszhat. Hányféle kiválasztás lehetséges? $d)$ Mennyi az esélye annak, hogy az egyik női versenyző, Tímea, egyik párosba sem kerül be?  (16 pont)   Megoldás. $a)$ Ha minden csúcsnak 9 lenne a fokszáma, akkor a fokszámok összege $12\cdot 9=108$ lenne. Az 56 él miatt a fokszámok összege 112, a különbség 4. Egy csúcs maximális fokszáma 11 lehet, tehát lehet két 11 fokszámú csúcs és 10 csúcs, aminek 9 a fokszáma. Ez megvalósítható úgy, hogy egy 12 pontú teljes gráfban két pontban minden élt meghagyunk. A maradék 10 pontot egy szabályos 10 szög csúcsainak képzelve elhagyjuk a szomszédos csúcsokat összekötő éleket. Ekkor ezek fokszáma 9-re csökken. Tehát legalább kettő 9-nél nagyobb fokszámú csúcsa van a gráfnak. $b)$ A 11 pontú teljes gráf éleinek száma $\frac{11\cdot 10}{2}=55$. Mivel ennek a gráfnak 56 éle van, így a 12. pontból is indul legalább egy él, ezért a gráf összefüggő. 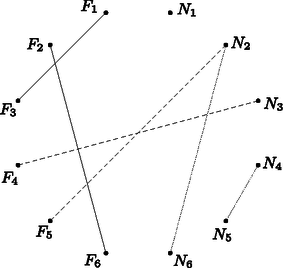$c)$ A 6 férfiversenyző közül két férfi pároshoz kell kiválasztani játékosokat, úgy, hogy egy férfi játékos nem szerepelhet mindkét párosban (ábra).     Ez $n_{\text{F}}=\frac{6\cdot 5}{2}\cdot \frac{4\cdot 3}{2}=90$-féleképpen lehetséges. Hasonlóan $n_{\text{N}}=90$-féleképpen lehet kiválasztani a női páros tagjait a 6 nő közül. A vegyes páros tagja bármelyik nő és bármelyik férfi lehet, mert eddig mindenki legfeljebb egy párosban szerepel. Így a két vegyes páros tagjait $n_{\text{V}}=6\cdot 6\cdot 5\cdot 5=900$-féleképpen lehet kiválasztani. Összesen tehát $n_{\text{ö}}=n_{\text{F}}\cdot n_{\text{N}}\cdot n_{\text{V}}=7290000$ féle kiválasztás lehetséges. $d)$ Ha Tímea egyik párosba sem kerül be, akkor a női párosok tagjait csak 5 nő közül választhatjuk ki, így $n_{\text{N1}}=\frac{5\cdot 4}{2}\cdot \frac{3\cdot 2}{2}=30$. A vegyes páros tagjait 6 férfi és 5 nő közül választhatjuk, vagyis $n_{\text{V1}}=6\cdot 5\cdot 5\cdot 4=600$. Tehát a kedvező esetek száma: $n_{\text{K}}=n_{\text{F}}\cdot n_{\text{N1}}\cdot n_{\text{V1}}=1620000$. Így annak az esélye, hogy Tímea egyik párosba sem kerül be: $\begin{array}{c}{\displaystyle p=\frac{n_{\text{ö}}}{n_{\text{K}}}=\frac{1620000}{7290000}=0\mathrm{,}2=20\%\mathrm{.}}\end{array}$