|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Monte-Carlo híres a kaszinóiról és az ott folyó szerencsejátékról. A szerencsejátékok kapcsolata a matematikával a XVII. században Pascal és Fermat munkásságával kezdődött. A szerencsejátékok, és általában a véletlen jelenségek több érdekes és nehezen megoldható matematikai problémát eredményeztek. A megoldásukkal olyan kérdésekre kaptak választ, melyek régóta foglalkoztatták a játékosokat. A kedvelt játékokról megállapították, hogy melyik fél számára mennyire ,,nyerő''. Természetesen az is nyilvánvaló volt, hogy a kiszámított valószínűségeket egyetlen játékra nincs értelme alkalmazni, hanem sok játék eredményét kell följegyezni és összegezni. A játékok nem vesztettek varázsukból, ugyanakkor igazi kihívás volt a matematikusoknak egy-egy valószínűség kiszámítása.
A XX. század közepén a számítógépek megjelenésével a szerencsejáték és a matematika is új lehetőségeket nyert. A kiszámított valószínűségeket ,,ellenőrizni'' is lehetett nagyszámú kísérlettel. Csak meg kellett tanítani a számítógépet kockát dobni: a gép -szer elvégez egy kísérletet, és minden kísérletben véletlenszerűen választ a lehetőségek közül. Az így nyert relatív gyakoriságok és a matematikai úton számított valószínűségek összevethetők voltak.
A Monte-Carlo-módszerek egy speciális problémamegoldási lehetőséget jelentenek, melyeket sikerrel alkalmaztak a matematika, fizika valamint az informatika területén. Az alapgondolat az előbbi ,,ellenőrzés'' fordítottja. Mit tehetünk akkor, ha a vizsgált jelenség bizonyos értékei nem kiszámíthatók, tehát nincs zárt, könnyen kiértékelhető formula az eredmény meghatározására? Az egyik út már ismert volt a számítógépek előtt: numerikus módszerekkel meg lehetett határozni olyan számítási lépéseket, melyek megfelelő pontossággal megközelítik a keresett mennyiségeket. A numerikus módszerek alkalmazásában is nagy segítség volt a számítógép. A Monte-Carlo-módszer mást javasol: szimuláljuk sokszor a problémához kapcsolható kísérletet, és a kapott eredmények alapján adjunk közelítést a keresett ismeretlen értékekre.
Lássuk először egy klasszikus valószínűségszámítás feladatnál a módszer működését: a 2008. márciusi számunkban megjelent B. 4080. feladat: A körvonalon egymástól függetlenül véletlenszerűen kiválasztunk 3 pontot. Mi annak a valószínűsége, hogy az általuk meghatározott háromszög hegyesszögű?
A feladat több szép megoldása olvasható honlapunkon, ezért nem volna szükségünk a Monte-Carlo-módszerre, hogy az eredményt közelítsük, mégis tanulságos a példa. A kísérletben véletlenszerűen elhelyezünk pontokat egy egységsugarú körön, majd meghatározzuk a kapott háromszög szögeit, és megállapítjuk, hogy hegyesszögű-e. A kísérletet -szer elvégezve megszámoljuk a hegyesszögű háromszögeket. Ha ezek száma , akkor a kísérletsorozatban a hegyesszögű háromszögek előfordulásának relatív gyakoriságát kapjuk, ami elég nagy esetén megfelelően pontos lesz. Kérdés ugyanakkor, hogy pl. két tizedesjegy pontossághoz milyen értéket érdemes megadni, de ezt hagyjuk későbbre, most foglalkozzunk a kísérletsorozatot megvalósító programmal.
Próbáljuk meg elkészíteni a számítógépes programot. Legyen egy egységkör a koordináta-rendszer kezdőpontjában, és , és a véletlenszerűen választott csúcsok. A legtöbb programozási nyelvben megtalálhatók véletlenszámok, pl. egy valós értéket kaphatunk a intervallumból (jelöljük ezt RND-vel). Azt a kérdést, hogy a számítógép miként állít elő véletlen értéket, hagyjuk későbbre. Amit biztosan tudnunk kell RND-ről, hogy egy futó program egymást követő RND értékét ábrázolva az egység intervallumon, azok nagyjából egyenletes sűrűséggel helyezkednek el. Azaz minél nagyobb a pontok száma, annál jobban teljesül, hogy az intervallum bármely szakaszának hossza, és a rajta megtalálható pontok száma között egyenes arányosság áll fönn. Első ötletünk, hogy RND értékét 2-vel megszorozva és 1-gyel csökkentve máris adódik mindhárom csúcs koordinátája. Az koordináták számításához használjuk a Pitagorasz-tételt, illetve egy-egy másik véletlenszámot: ha ez utóbbi 0,5-nél kisebb, akkor a pozitív, egyébként a negatív koordinátát válasszuk. Így véletlenszerűen kijelöltünk három pontot a köríven, már csak a szögeket kell kiszámolni. A kísérletet sokszor elvégezve egy relatív gyakorisággal tudjuk közelíteni a keresett értéket.
Gondoljuk meg, hogy helyesen jártunk-e el. Tanulmányainkból tudjuk, hogy a valószínűség klasszikus kiszámítási módja, a kedvező és összes esetek hányadosa csak akkor adja a valószínűséget, ha a kísérletben szereplő elemi események mind egyenlő valószínűséggel következnek be. Hasonlóan figyelnünk kell a geometriai valószínűség meghatározásakor is. Mivel jelen esetben a csúcsok egy köríven helyezkednek el, ezért szükséges, hogy ott bármely két azonos hosszúságú ívre ,,közel'' azonos számú pont kerüljön. A koordináták előbbi megválasztásával azonban ezt az íveknél nem teljesítettük (ld. bal oldali ábra), mivel ott két azonos hosszúságú szakaszhoz két különböző hosszúságú ív tartozik. Akkor járunk el helyesen, ha az RND értékét adó intervallumot a körívnek feleltetjük meg. Tehát egy véletlen csúcsot pl. az tengelytől adott irányban fölmért szög jelöl ki a körvonalon.
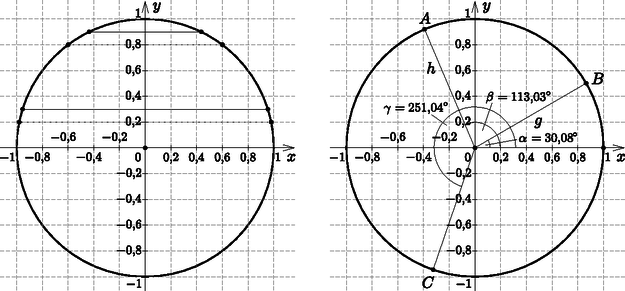
A program feladata a következő: számú kísérletet végez, és minden esetben megállapítja, hogy a kapott pontok egy hegyesszögű háromszög csúcsai-e. Megszámolja ezeket, és a kapott darabszámot a végén elosztja -nel.
Eljárás Hegy3korvonal(N)
k := 0 (hegyesszögű háromszögek száma)
Ciklus h := 1-től N-ig
alfa :=
ax := cos(alfa) : ay := sin(alfa)
beta := 2 π*RND(0,1)
bx := cos(beta) : by := sin(beta)
gamma := 2 π*RND(0,1)
cx := cos(gamma) : cy := sin(gamma)
Ha hegyes(ax,ax,bx,by,cx,cy) akkor k := k+1
Ciklus vége
Ki: k/N
Eljárás vége
Az eljárásban szereplő hegyes() függvény megállapítja, hogy a kapott koordinátákkal jellemzett háromszög hegyesszögű-e. Ehhez a szögek pontos nagyságát nem kell meghatározni, csak azt, hogy derékszögnél nagyobb, kisebb, vagy vele egyenlő-e. Például az A csúcsnál lévő szögről elég információt ad az AB→⋅AC→ skaláris szorzat előjele. A függvény mindhárom skaláris szorzat pozitív értéke esetén ad igaz választ. Ennek elkészítését az olvasóra bízzuk.
Változtassuk meg a feladatot úgy, hogy most a pontok egy körlapon találhatók! Akkor járunk el helyesen, ha biztosítjuk, hogy a körlapon véletlenszerűen helyezkedjenek el a csúcsok. Minél több kísérletet végzünk, annál jobban teljesülnie kell, hogy a véletlenszerűen választott pontok ,,egyenletes sűrűséggel'' vannak elszórva a körlapon. Pontosabban fogalmazva: legyen a körlap egy T1 és T2 területű részére eső véletlen pontok száma P1 és P2. A kísérletek számának növelésével a P1/P2 hányados közelíti a T1/T2 értékét, miközben N értéke növekszik.
A körvonalnál láttuk, hogy a kapott [0,1[ intervallumot kibővítettük [0,2π[ intervallummá. Most területekről van szó, így jó gondolatnak tűnik, hogy egy véletlen csúcs x és y koordinátáját jelentse egy-egy RND érték. Ekkor azonban egy egység oldalú négyzeten oszlanak el egyenletesen a pontok. Ez nem jelent gondot, ha az egységsugarú körön kívüli pont esetén újra próbálkozunk, és egy másik véletlen számpárt kérünk. Ezzel persze tovább tart a program futása, de a megoldás a kitűzött feladatot oldja meg. A program ezek alapján a következő:
Eljárás Hegy3korlap(N)
k := 0 (hegyesszögű háromszögek száma)
Ciklus h := 1-től N-ig
ax := RND(0,1) : ay := RND(0,1)
Ciklus amíg ax2+ay2 > 1
ax := RND(0,1) : ay := RND(0,1)
Ciklus vége
... hasonlóan a másik két csúccsal
Ha hegyes(ax,ax,bx,by,cx,cy) akkor k := k+1
Ciklus vége
Ki: k/N
Eljárás vége
A feladat tovább bővíthető, pl. fölvethető, hogy a körvonalon vagy a körlapon véletlenszerűen választott pontok átlagosan mekkora kerületű, területű háromszöget határoznak meg. Ez utóbbi feladatok eredménye összetett számításokkal kapható, míg Monte-Carlo-módszerrel az eddigiekhez hasonlóan.
Lapunk korábbi számaiban foglalkoztunk a témával, a megjelent cikkek közül most Cserti László: A munkára fogott véletlen, I. részét ajánlanánk, amelyben több jó példát láthatunk a módszer használatára.
http://db.komal.hu/KomalHU/showpdf.phtml?tabla=Cikk&id=200459. |
 PDF | MathML
PDF | MathML 