Cím:	Megoldásvázlatok a 2018/1. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Varga Péter
Füzet:	2018/február, 80 - 88. oldal	PDF  |  MathML
Hivatkozás(ok):	2018/január: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán az alábbi egyenletrendszert: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 4\cdot 2^x+5^y}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle 8\cdot 2^x+3\cdot 5^y}& {\displaystyle =5.}\hfill \end{array}}}\end{array}$ (5 pont) $b)$ Oldjuk meg a $\left[\pi ;2\pi \right]$ intervallumon az alábbi egyenletet: $\begin{array}{c}{\displaystyle 3\cdot \text{tg}{}^{2}x-2\sqrt[]{3}\cdot \text{tg}x-3=0.}\end{array}$ (5 pont)   Megoldás. $a)$ I. megoldás. Az első egyenletből $5^y=2-4\cdot 2^x$, melyet a második egyenletbe helyettesítve és rendezve $4\cdot 2^x=1$. Az exponenciális függvény szigorú monotonitása miatt $x=-2$, $y=0$. Az eredeti egyenletrendszerbe történő behelyettesítés után láthatjuk, hogy a kapott számpár valóban megoldás. II. megoldás. Az első egyenlet háromszorosából a második egyenletet kivonva: $4\cdot 2^x=1$. Az exponenciális függvény szigorú monotonitása miatt $x=-2$, $y=0$. Az eredeti egyenletrendszerbe történő behelyettesítés után láthatjuk, hogy a kapott számpár valóban megoldás. $b)$ Az egyenlet $\text{tg}x$-ben másodfokú, melynek gyökei: $\text{tg}x=\sqrt[]{3}$ és $\text{tg}x=-\frac{\sqrt[]{3}}{3}$. $\text{tg}x=\sqrt[]{3}$ a $\left[\pi ;2\pi \right]$ alaphalmazon pontosan akkor teljesül, ha $x=\frac{4\pi }{3}$, $\text{tg}x=-\frac{\sqrt[]{3}}{3}$ a $\left[\pi ;2\pi \right]$ alaphalmazon pontosan akkor teljesül, ha $x=\frac{11\pi }{6}$. A két értéket behelyettesítve az eredeti egyenletbe meggyőződhetünk róla, hogy mindkettő megoldás.   2. A Mölkky egy finn ügyességi játék, amit tizenkét darab fabábuval játszanak. A bábukat 5,5 cm átmérőjű, 15 cm magas egyenes körhenger alakú fából készítik úgy, hogy a henger tetejét az 1. ábrán látható módon ${45}^{\circ }$-os szögben levágják, majd a bábuk tetejére 1‐12-ig sorszámokat rajzolnak. 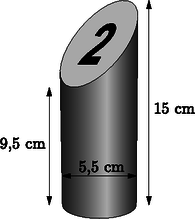  1. ábra   $a)$ Mekkora egy, a játékhoz használt fabábu térfogata?  (4 pont) A játék kezdetén a bábukat a 2. ábrán látható elrendezésben egy keret segítségével szorosan egymás mellé illesztik, hogy azok érintsék egymást.   2. ábra   $b)$ Mekkora a keret kerülete?  (4 pont) A játék elején a játékosok egy dobófával (Mölkky-vel) próbálják feldönteni a keretben elhelyezkedő tizenkét számozott fabábut. A keretet a dobás előtt leveszik a bábukról. Az egymásra vagy a dobófára támaszkodó bábuk nem számítanak feldőltnek, a szabályosan feldőlt bábunak párhuzamosnak kell lennie a talajjal. Ennek következtében bármilyen kombinációban fel lehet dönteni a bábukat. $c)$ Hányféleképpen lehet egy dobásból három bábut feldönteni úgy, hogy a feldöntött bábukon szereplő számok szorzata négyzetszám legyen?  (5 pont)   Megoldás. $a)$ A játékhoz használt fabábuk egy 5,5 cm átmérőjű 9,5 cm magasságú egyenes körhengerből, és egy 5,5 cm átmérőjű és 5,5 cm magasságú ,,félhengerből'' állnak. Egy 5,5 cm átmérőjű 9,5 cm magas egyenes körhenger térfogata: $\begin{array}{c}{\displaystyle V_1=2\mathrm{,}{75}^2\cdot \pi \cdot 9\mathrm{,}5\left(\approx 225\mathrm{,}7{\text{cm}}^3\right)\mathrm{.}}\end{array}$ Egy 5,5 cm átmérőjű és magasságú ,,félhenger'' térfogata: $\begin{array}{c}{\displaystyle V_2=\frac{2\mathrm{,}{75}^2\cdot \pi \cdot \mathrm{5,5}}{2}\left(\approx 65\mathrm{,}3{\text{cm}}^3\right)\mathrm{.}}\end{array}$ Egy, a játékhoz használt fabábu térfogata kerekítve: $V_1+V_2\approx 291{\text{cm}}^3$.   Megjegyzés. A keresett térfogat úgy is számolható, hogy egy 5,5 cm átmérőjű, 15 cm magas egyenes körhenger térfogatából kivonjuk egy 5,5 cm átmérőjű és magasságú ,,félhenger'' térfogatát.   $b)$ A keret 3 db $4r$ és 3 db $2r$ hosszúságú egyenes szakaszból, valamint 6 db $r$ sugarú $\alpha$ középponti szögű körcikkből áll. Az egyes körcikkek középponti szöge ${60}^{\circ }$, ezért a hat körcikk együtt egy $r$ sugarú (teljes) kört ad ki. A keret kerülete: $K=3\cdot 4\cdot 2\mathrm{,}75+3\cdot 2\cdot 2\mathrm{,}75+2\cdot 2\mathrm{,}75\cdot \pi \approx 66\mathrm{,}78$ cm. $c)$ A feldöntött bábukon szereplő 3 szám szorzata négyzetszám lesz, ha 3 db különböző négyzetszámmal jelölt bábut döntünk fel, mely pontosan 1-féleképpen lehetséges: $\left(1;4;9\right)$. Ha 2 db négyzetszámmal és 1 db nem négyzetszámmal jelölt bábut döntünk fel, akkor a szorzat nem lehet négyzetszám. Ha 1 db négyzetszámmal és 2 db nem négyzetszámmal jelölt bábut döntünk fel, akkor ez utóbbi két szám között nem szerepelhet az 5, 7, 10 és 11 egyike sem (5 és 10 együtt sem). A megmaradó 2; 3; 6; 8; 12 számok közül kiválasztható 10 számpár közül csak a $\left(2;8\right)$ és $\left(3;12\right)$ felel meg, így a lehetséges esetek: $\left(1;2;8\right)$, $\left(1;3;12\right)$, $\left(4;2;8\right)$, $\left(4;3;12\right)$, $\left(9;2;8\right)$, $\left(9;3;12\right)$. Ha 0 db négyzetszámmal és 3 db nem négyzetszámmal jelölt bábut döntünk fel, akkor ezek között az 5 és 10 csak egyszerre szerepelhet, és ekkor a harmadik szám 2 vagy 8 lehet. A 2; 3; 6; 8; 12 számok közül kiválasztható 10 számhármas közül csak négy felel meg, így a lehetséges esetek: $\left(2;3;6\right)$, $\left(2;5;10\right)$, $\left(2;6;12\right)$, $\left(3;6;8\right)$, $\left(5;8;10\right)$, $\left(6;8;12\right)$. Tehát összesen 13-féle különböző feldöntés lehetséges.   3. Adott a derékszögű koordináta-rendszerben két pont: $A\left(1;-2\right)$ és $B\left(3;12\right)$. $a)$ Határozzuk meg az $x$ tengely azon $P$ pontjának koordinátáit, melyre az $ABP$ háromszög egyenlő szárú.  (7 pont) $b)$ Számítsuk ki, hogy az $x$ tengely melyik pontjából látható derékszögben az $AB$ szakasz.  (7 pont)   Megoldás. $a)$ Ha $AP=BP$ (vagyis az egyenlő szárú háromszög alapja $AB$) és $P\left(x;0\right)$, akkor ${\left(x-1\right)}^2+4={\left(x-3\right)}^2+144$, melyből $x=37$. Ha $AB=AP$ (vagyis az egyenlő szárú háromszög alapja $BP$) és $P\left(x;0\right)$, akkor ${4+196=\left(x-1\right)}^2+4$, melyből $x$ értékei $-13$ és $15$. Ha $AB=BP$ (vagyis az egyenlő szárú háromszög alapja $AP$) és $P\left(x;0\right)$, akkor $4+196={\left(x-3\right)}^2+144$, melyből $x$ értékei $3+2\sqrt[]{14}\left(\approx 10\mathrm{,}48\right)$ és $3-2\sqrt[]{14}\left(\approx -4\mathrm{,}48\right)$. Tehát a keresett pontok kerekítéssel: $P_1\left(37;0\right)$; $P_2\left(-13;0\right)$; $P_3\left(15;0\right)$; $P_4\left(10\mathrm{,}48;0\right)$ és $P_5\left(-4\mathrm{,}48;0\right)$. $b)$ I. megoldás. A keresett $Q$ pont koordinátáit (a Thalész-tétel megfordítása miatt) az $AB$ szakasz fölé, mint átmérő fölé rajzolt kör és az $x$ tengely metszéspontja adja meg. A kör középpontja az $AB$ szakasz felezőpontja: $\left(\frac{1+3}{2};\frac{-2+12}{2}\right)=\left(2;5\right)$. A kör sugara: $\begin{array}{c}{\displaystyle r=\frac{AB}{2}=\frac{\sqrt[]{{\left(3-1\right)}^2+{\left(12+2\right)}^2}}{2}=5\sqrt[]{2}\mathrm{.}}\end{array}$ A kör egyenlete: ${\left(x-2\right)}^2+{\left(y-5\right)}^2=50$. A kör $x$ tengellyel való metszéspontját az $y=0$ helyettesítéssel kapjuk, így ${\left(x-2\right)}^2=25$, melyből $x_1=-3$ és $x_2=7$. Tehát a keresett pontok: $Q_1\left(-3;0\right)$ és $Q_2\left(7;0\right)$. II. megoldás. Mivel a $Q$ pont az $x$ tengelyen van, így a második koordinátája 0, vagyis $Q\left(x;0\right)$. $\overrightarrow{AQ}=\left(x-1;2\right)$ és $\overrightarrow{BQ}=\left(x-3;-12\right)$. Az $\overrightarrow{AQ}$ és $\overrightarrow{BQ}$ vektorok pontosan akkor merőlegesek egymásra, ha skaláris szorzatuk 0, vagyis $\left(x-1\right)\cdot \left(x-3\right)+2\cdot \left(-12\right)=0$. Az előbbi egyenletet rendezve $x^2-4x-21=0$, ahonnan $x_1=-3$ és $x_2=7$. Tehát a keresett pontok: $Q_1\left(-3;0\right)$ és $Q_2\left(7;0\right)$.   4. A 3. ábrán egy négyemeletes, 60 cm magas esküvői torta látható, melynek szintjei különböző magasságú és sugarú egyenes hengerek. Az egyes szintek magasságainak hosszai mértani sorozatot alkotnak. $a)$ Milyen magasak az egyes emeletek, ha a legfelső szint 4 cm magas, és a többi szint magasságának mérőszáma is egész szám?  (9 pont) 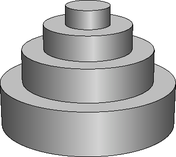  3. ábra   Az esküvői torta 16 cm átmérőjű, 4 cm magas legfelső szintjét a 4. ábrán látható módon díszítéssel látják el.   4. ábra   $b)$ Milyen hosszú a legfelső szintre tekert díszítőcsík, ha a szélességétől eltekintünk?  (5 pont)   Megoldás. $a)$ I. megoldás. Jelölje $q$ a mértani sorozat hányadosát. A feladat szövege alapján a mértani sorozat összegképletébe helyettesítve: $60=4\cdot \frac{q^4-1}{q-1}$ $\left(q\ne 1\right)$, melyet rendezve: $15q-q^4=14$, majd $q$-t kiemelve: $q\left(15-q^3\right)=14$. Mivel az egyes szintek magasságainak mérőszáma egész szám, ezért az előbbi szorzótényezők 14 pozitív osztói. A lehetséges osztópárok: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi></math>}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{ 7}}\hfill & \hfill {\displaystyle \text{14 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mn>15</mn><mo stretchy="false">-</mo><mrow><msup><mrow><mi>q</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}}\hfill & \hfill {\displaystyle \text{14}}\hfill & \hfill {\displaystyle \text{ 7}}\hfill & \hfill {\displaystyle \text{ 2}}\hfill & \hfill {\displaystyle \text{1 }}\hfill \\ \hline\end{array}}}\end{array}$ Ezek közül a harmadik és negyedik eset nem ad jó megoldást (a kétféleképpen számított $q$ érték nem egyezik meg). Ha $q=1$, akkor egy állandó tagú mértani sorozatot kapunk, mely a feladat szövegének nem felel meg. Ha $q=2$, akkor az esküvői torta egyes szintjeinek magassága 4 cm; 8 cm; 16 cm; 32 cm, mely megfelel a feladat feltételeinek. II. megoldás. Jelölje $q$ a mértani sorozat hányadosát. A feladat szövege alapján a mértani sorozat összegképletébe helyettesítve: $\begin{array}{c}{\displaystyle 60=4\cdot \frac{q^4-1}{q-1}\left(q\ne 1\right)\mathrm{.}}\end{array}$ A nevezetes azonosságok segítségével a számlálót szorzattá alakítva: $\begin{array}{c}{\displaystyle 15=\frac{\left(q^2-1\right)\left(q^2+1\right)}{q-1}\mathrm{,}}\end{array}$ majd egyszerűsítve $15=\left(q+1\right)\cdot \left(q^2+1\right)$. Mivel az egyes szintek magasságainak mérőszáma egész szám, ezért az előbbi szorzótényezők 15 pozitív osztói. A lehetséges osztópárok: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|ccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>q</mi><mo stretchy="false">+</mo><mn>1</mn></math>}}\hfill & \hfill {\displaystyle \text{1}}\hfill & \hfill {\displaystyle \text{ 3}}\hfill & \hfill {\displaystyle \text{ 5}}\hfill & \hfill {\displaystyle \text{15 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>q</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">+</mo><mn>1</mn></math>}}\hfill & \hfill {\displaystyle \text{15}}\hfill & \hfill {\displaystyle \text{ 5}}\hfill & \hfill {\displaystyle \text{ 3}}\hfill & \hfill {\displaystyle \text{1 }}\hfill \\ \hline\end{array}}}\end{array}$ Ezek közül az első, harmadik és negyedik eset nem ad jó megoldást (a kétféleképpen számított $q$ érték nem egyezik meg). Ha $q=2$, akkor az esküvői torta egyes szintjeinek magassága 4 cm; 8 cm; 16 cm; 32 cm, mely megfelel a feladat feltételeinek. $b)$ A torta legfelső szintjét alkotó egyenes henger palástját a díszítővonal két végpontját összekötő alkotó mentén történő felvágással (kiterítve), egy $16\pi$ cm széles, 4 cm magas téglalapot kapunk, amelyen négy egyforma hosszúságú vonal húzódik párhuzamosan. Tekintsünk egy $16\pi$ cm és 1 cm befogójú derékszögű háromszöget, melyben a Pitagorasz-tétel szerint a díszítővonal hossza $\sqrt[]{{\left(16\pi \right)}^2+1^2}$ (cm). Tehát a díszítővonalak összhosszúsága $4\cdot \sqrt[]{{\left(16\pi \right)}^2+1^2}$, melynek egy tizedesjegyre kerekített értéke 201,1 cm.   II. rész     5. Adott a valós számok halmazán értelmezett $f$ és $g$ függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=5-2x\text{és}g\left(x\right)=2x^2-3x+1.}\end{array}$ $a)$ Adjuk meg a $g\circ f$ függvény zérushelyeit.  (4 pont) $b)$ Számítsuk ki a $\underset{-1}{\overset{1}{\int }}f\left(x\right)\text{d}x-\underset{-1}{\overset{1}{\int }}\left(g\left(x\right)+1\right)\text{d}x$ határozott integrált.  (4 pont) $c)$ Írjuk fel a $g$ függvény $f$ függvényre merőleges érintőjének egyenletét.  (8 pont)   Megoldás. $a)$ $\left(g\circ f\right)\left(x\right)=g\left(f\left(x\right)\right)=2{\left(5-2x\right)}^2-3\left(5-2x\right)+1=8x^2-34x+36$. A $8x^2-34x+36=0$ egyenlet gyökei a keresett zérushelyek, melyek $x_1=2$ és $x_2=\frac{9}{4}$. $b)$ ${\displaystyle \begin{array}{c}\hfill {\displaystyle \underset{-1}{\overset{1}{\int }}f\left(x\right)\text{d}x-\underset{-1}{\overset{1}{\int }}\left(g\left(x\right)+1\right)\text{d}x=\underset{-1}{\overset{1}{\int }}\left(-2x^2+x+3\right)\text{d}x={\left[-2\cdot \frac{x^3}{3}+\frac{x^2}{2}+3x\right]}_{-1}^1=}\hfill \\ \hfill {\displaystyle =\left(-2\cdot \frac{1^3}{3}+\frac{1^2}{2}+3\cdot 1\right)-\left(-2\cdot \frac{{\left(-1\right)}^3}{3}+\frac{{\left(-1\right)}^2}{2}+3\cdot \left(-1\right)\right)=\left(-\frac{4}{3}\right)+6=\frac{14}{3}\mathrm{.}}\hfill \end{array}}$ $c)$ I. megoldás. Az $f$ függvény grafikonja olyan egyenes (mely nem párhuzamos a koordinátatengelyekkel), melynek meredeksége $-2$, ezért az $f$ függvény grafikonjára merőleges érintő egyenes $y=\frac{1}{2}x+b$ alakú, ahol $b$ valós paraméter. Az előbbi egyenesek közül az lesz a parabola érintője, amelynek egy közös pontja van a megadott parabolával. Az előbbiek miatt az alábbi egyenletrendszernek csak egy valós számpár lehet a megoldása: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =2x^2-3x+\mathrm{1,}}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =\frac{1}{2}x+b\mathrm{.}}\hfill \end{array}}$ A két jobb oldali kifejezés egyenlőségéből: $2x^2-3x+1=\frac{1}{2}x+b$, melyből $4x^2-7x+2-2b=0$. Az előbbi paraméteres másodfokú egyenletnek pontosan akkor van egy valós gyöke, ha diszkriminánsa 0, azaz: ${\left(-7\right)}^2-4\cdot 4\cdot \left(2-2b\right)=0$, melyből $b=-\frac{17}{32}$. A keresett érintő egyenlete: $y=\frac{1}{2}x-\frac{17}{32}$. II. megoldás. Az $f$ függvény grafikonja olyan egyenes (mely nem párhuzamos a koordinátatengelyekkel) melynek meredeksége $-2$, ezért az $f$ függvény grafikonjára merőleges érintő meredeksége $\frac{1}{2}$. A parabola $P_0\left(x_0;y_0\right)$ pontban húzott érintőjének meredekségét a $g$ deriváltfüggvényének az $x_0$ helyen felvett helyettesítési értéke adja meg: $g\text{'}\left(x_0\right)=4x_0-3$. A meredekségek egyenlősége miatt: $4x_0-3=\frac{1}{2}$, melyből $x_0=\frac{7}{8}$. Az érintési pont második koordinátája a parabola egyenletébe történő $x_0=\frac{7}{8}$ helyettesítésből: $y_0=-\frac{3}{32}$. Az adott ponton átmenő, adott iránytangensű egyenes egyenletébe helyettesítve: $\begin{array}{c}{\displaystyle y+\frac{3}{32}=\frac{1}{2}\cdot \left(x-\frac{7}{8}\right)\mathrm{,}}\end{array}$ melyből a keresett érintő egyenlete: $y=\frac{1}{2}x-\frac{17}{32}$.   6. $a)$ Egy $6$ pontú fagráfban a csúcsok fokszámainak terjedelme $2$, módusza $1$. Hány ilyen különböző $6$ pontú fagráf létezik, ha csúcsaikat nem különböztetjük meg egymástól?  (8 pont) $b)$ Hány csúcsa van annak a fagráfnak, amelyben az össze nem kötött pontpárok száma kétszerese az élek számának?  (8 pont)   Megoldás. $a)$ Ha a módusz 1, a terjedelem 2, akkor a legkisebb fokszám 1, a legnagyobb pedig 3. Három darab olyan különböző (páronként nem izomorf) 6 pontú (5 élű) fagráf van, amelyben a legnagyobb fokszám 3:     Ezek közül mindhárom megfelelő. $b)$ Az $n$ pontú fagráf éleinek száma $n-1$. Ha az $n$ pontú teljes gráf éleinek számából kivonjuk az $n$ pontú fagráf éleinek számát, megkapjuk a fagráf össze nem kötött pontpárjainak a számát, ezért a mi esetünkben: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\left(n-1\right)=2\left(n-1\right)\mathrm{.}}\end{array}$ Az egyenletet 2-vel szorozva, majd rendezve: $n\left(n-1\right)=6\left(n-1\right)\mathrm{,}$ melyből $\left(n-1\right)\left(n-6\right)=0$, melynek megoldásai $n_1=1$ és $n_2=6$. Ha 1 pontú a fagráf, akkor 0 éle van. Ekkor az össze nem kötött pontpárok száma is 0, és ez kétszerese az élek számának. Ha 6 pontú a fagráf, akkor az éleinek száma 5. Ekkor az össze nem kötött pontpárok száma 10, és ez kétszerese az élek számának.   7. Egy iskolai büfé italautomatájában hétféle rostos üdítő, kétféle ásványvíz és háromféle szénsavas frissítő kapható, mindegyikből pontosan 8 db. $a)$ Hányféle sorrendben vehet ki Emese mindegyik rostos üdítőből pontosan egyet?  (2 pont) $b)$ Hányféleképpen választhat ki Emese 3 db innivalót tetszőleges összeállításban, ha az automatában lévő összes üdítőt különbözőnek tekintjük?  (5 pont) Az italautomaták elég gyakran elromlanak. Egy italautomatákat szervizelő cégnél 0,05 annak a valószínűsége, hogy egy adott napon nincs javítanivaló; 0,2, hogy pontosan egy; 0,6, hogy pontosan két javítanivaló automata van. $c)$ Mekkora annak a valószínűsége, hogy öt egymást követő munkanapon nincs javítanivaló?  (3 pont) $d)$ Mekkora annak a valószínűsége, hogy három nap alatt összesen két gépet kell megjavítaniuk?  (6 pont)   Megoldás. $a)$ Mivel Emese mindegyik fajta rostos üdítőből pontosan egyet választ, ezért 7 különböző elem ismétlés nélküli permutációját kell kiszámítani. Emese $7!\left(=5040\right)$-féle sorrendben veheti ki az üdítőket. $b)$ Mivel egy italautomatából adott sorrendben potyognak ki az üdítők, ezért a következő lehetőségek vannak. Három ugyanolyan üdítőt választ, ezt 12-féleképp teheti meg. Kettő ugyanolyat és egy másmilyet választ, ezt $12\cdot 11=132$-féleképp tudja megtenni. Végül, ha mindhárom üdítőital különböző típusú, arra $\left(\genfrac{}{}{0ex}{}{12}{3}\right)=220$ lehetőség van. Összesen 364-féleképpen választhatja ki a 3 üdítőt tetszőleges összeállításban.. $c)$ Annak a valószínűsége, hogy egy adott napon nincs javítanivaló 0,05; annak, hogy van 0,95. Annak a valószínűsége, hogy 5 egymást követő napon nincs javítanivaló: $0\mathrm{,}{05}^5=0\mathrm{,}0000003125$. $d)$ Két esetet különböztethetünk meg: 1. a három nap közül az egyiken van két javítanivaló és a másik két napon semmi, vagy 2. két napon van egy-egy javítanivaló és egy napon semmi. Mindkét esetben a napok sorrendje 3-féle lehet, ezért az első eset bekövetkezésének valószínűsége $3\cdot 0\mathrm{,}05\cdot 0\mathrm{,}05\cdot 0\mathrm{,}6$ $\left(=0\mathrm{,}0045\right)$, míg a második eset bekövetkezésének valószínűsége $3\cdot 0\mathrm{,}05\cdot 0\mathrm{,}2\cdot 0\mathrm{,}2$ $\left(=0\mathrm{,}006\right)$. A kérdezett valószínűség az előbbi két valószínűség összege, vagyis $0\mathrm{,}0105$.   8. Egy egyetem gólyatáborában két csoport szkanderbajnokságot játszik egymással. Azért, hogy felmérjék az erőviszonyokat, először a két csoporton belül mindenki mindenkivel egyszer játszik, majd ezt követően a csoportok tagjai megmérkőznek a másik csoport tagjaival. A játék során a csoportokban összesen $144$, míg a csoportok között $156$ megmérettetésre kerül sor. $a)$ Hányan vannak az egyik, és hányan a másik csoportban?  (9 pont) A bajnokság megkezdése előtt minden versenyző kap egy sorszámot. $b)$ Botond azt állítja, hogy az egyjegyű sorszámot kapott versenyzők közül ki lehet választani hatot úgy, hogy bárhogy párosítjuk őket, a párokban szereplő versenyzők sorszámainak összege három különböző szám lesz. Igaza van-e?  (7 pont)   Megoldás. $a)$ Jelölje az egyik csoportban lévők számát $n$, míg a másikét $m$. Ekkor a feladat szövege alapján: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{n\left(n-1\right)}{2}+\frac{m\left(m-1\right)}{2}}& {\displaystyle =\mathrm{144,}}\hfill \\ \hfill {\displaystyle n\cdot m}& {\displaystyle =156.}\hfill \end{array}}$ Az első egyenletet átalakítva $\left(n^2+m^2\right)-\left(n+m\right)=288$, majd az ${\left(a+b\right)}^2=a^2+2ab+b^2$ azonosságot alkalmazva az egyenlet ${\left(n+m\right)}^2-\left(n+m\right)-2nm=288$ alakban írható. Az $n\cdot m=156$ helyettesítéssel és rendezéssel az előbbi egyenlet a következőképpen írható: ${\left(n+m\right)}^2-\left(n+m\right)-600=0$, mely $\left(n+m\right)$-ben másodfokú, megoldásai $n+m=25$ és $n+m=-24$. Mivel $n\mathrm{,}m>0$, ezért az utóbbi nem lehetséges. Ha $n+m=25$ és $n\cdot m=156$, akkor a szimmetriától eltekintve pontosan egy olyan pozitív valós számpár van, mely kielégíti az eredeti egyenletrendszert, mégpedig: $n=12$ és $m=13$. A szöveg alapján történő ellenőrzéssel meggyőződhetünk, hogy a számpár megoldása a feladatnak. $b)$ Nevezzük a nem kiválasztott három versenyző sorszámát ,,visszamaradónak''. Az $\mathrm{1,2,3,4,5,6,7,8,9}$ számsorban a hat kiválasztott számot a három visszamaradó szám csak úgy választhatja szét, hogy legalább két helyen szomszédosak a kiválasztott számok. Ha a visszamaradó számok nem választják szét a kiválasztottakat (tehát a visszamaradók éppen az $\mathrm{1,2,3}$ vagy a $\mathrm{7,8,9}$), akkor is van legalább két helyen szomszédos szám. Ha a szomszédos kiválasztott számok között vannak olyanok, melyekre $a<a+1<b<b+1$ teljesül, akkor $a+\left(b+1\right)=\left(a+1\right)+b$, tehát van egyező összeg. Ha nincsenek ilyenek, akkor a két-két szomszédos szám az $a$, $a+1$ és az $a+1$, $a+2$. Ekkor a maradék három kiválasztott számot ezektől és egymástól is elválasztja egy-egy visszamaradó szám. Tehát van két kiválasztott szám, melyre vagy $a<a+1<a+2<b<b+2$, vagy $b-2<b<a<a+1<a+2$. Az első esetben $a+\left(b+2\right)=\left(a+2\right)+b$, a másodikban is lesz egyező összeg. Tehát Botondnak nincs igaza.   9. Egy szabályos háromszög alakú céltábla oldalait $n$ $(n>1$, $n\in \text{N})$ egyenlő részre osztottuk. Ezután az osztópontokon át a háromszög oldalaival párhuzamosan szakaszokat húztunk, melynek végpontjai a megfelelő osztópontok. Az így keletkező egybevágó szabályos kisháromszögeket balról jobbra, egyesével, felváltva feketére és fehérre színezzük úgy, hogy minden sorban az első kisháromszög fekete. $a)$ Mekkora annak a valószínűsége, hogy a céltáblára egyetlen lövést leadva, az fekete mezőt talál el, feltéve, hogy a lövés eltalálja a céltáblát?  (9 pont) $b)$ Határozzuk meg $a$ és $b$ értékét, ha tudjuk, hogy a kapott $p$ valószínűségre minden $n>1$ egész esetén teljesül, hogy $a<p\le b$, ahol $a$ a lehető legnagyobb, $b$ pedig a lehető legkisebb ilyen szám?  (7 pont)   Megoldás. $a)$ A feladat megértését tükröző ábra:     A keresett $A_n$ valószínűséget a fekete kisháromszögek területének aránya adja meg a $T$ területű céltáblán. A céltábla $T$ területe: $T=t\cdot n^2$, ahol $t$ a felosztás során keletkező egy kisháromszög területe. Az ábrát vizsgálva látszik, hogy a céltábla egyik csúcsától lefelé haladva az egymást követő sorokban a fekete háromszögek száma (és így területösszegük is) számtani sorozatot alkot, melynek első tagja és differenciája is $t$. Annak a valószínűsége, hogy a lövedék fekete mezőt talál el, a számtani sorozat első $n$ tagjának összegével arányos, ezért az összegképletbe behelyettesítve: $\begin{array}{c}{\displaystyle S_n=\frac{t+nt}{2}\cdot n=t\cdot \frac{n\left(n+1\right)}{2}\mathrm{.}}\end{array}$ A keresett $A_n$ valószínűség: $\begin{array}{c}{\displaystyle \frac{t\cdot \frac{n\left(n+1\right)}{2}}{t\cdot n^2}=\frac{n+1}{2n}\mathrm{.}}\end{array}$ $b)$ Felhasználva a korábban kapott összefüggést: $\begin{array}{c}{\displaystyle A_n=\frac{n+1}{2n}=\frac{1}{2}+\frac{1}{2n}\mathrm{.}}\end{array}$ Mivel az $\left(\frac{1}{n}\right)$ sorozat szigorúan monoton csökken és 0-hoz tart, ezért a fenti valószínűséget megadó $\left(\frac{1}{2}+\frac{1}{2n}\right)$ sorozat is konvergens és szigorúan monoton csökken, melynek határértéke: $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\left(\frac{1}{2}+\frac{1}{2n}\right)=\frac{1}{2}\mathrm{.}}\end{array}$ Az előbbiek miatt az $\left(\frac{1}{2}+\frac{1}{2n}\right)$ sorozat maximális értékét $n=2$ esetén veszi fel, ami $\frac{3}{4}$, ezért a keresett valószínűség: $\frac{1}{2}<A_n\le \frac{3}{4}$.