Cím: A 2017. évi Kürschák József Matematikai Tanulóverseny feladatainak megoldásai
Szerző(k):  Fleiner Tamás 
Füzet: 2018/február, 71 - 77. oldal  PDF  |  MathML 
Témakör(ök): Matematika, Kürschák József (korábban Eötvös Loránd), Szakmai cikkek

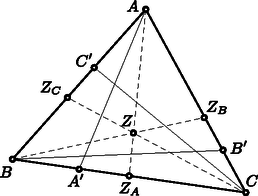
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

 
1. Legyen ABC tetszőleges háromszög, és válasszuk az A', B' és C' pontokat egymástól függetlenül, egyenletes eloszlással rendre a BC, CA és AB oldalakról. A sík Z pontja esetén jelölje p(Z) annak a valószínűségét, hogy az AA', BB' és CC' egyenesek által határolt háromszög tartalmazza Z-t. Határozzuk meg az ABC háromszögnek azt a Z belső pontját, amelyre p(Z) a lehető legnagyobb.
 
Megoldás. Legyenek ZA, ZB és ZC rendre az AZ, BZ és CZ egyenesek metszéspontjai az ABC háromszög szemközti oldalával. Jelölje
α:=BZABC,β:=CZBCA  és  γ:=AZCAB
azt, hogy ezek a pontok milyen arányban osztják az egyes oldalakat. Ekkor
ZACBC=BC-BZABC=1-BZABC=1-α,
és hasonlóan
ZBACA=1-β,illetveZCBAB=1-γ.


 
 

A Ceva-tétel alapján
1=BZAZAC⋅CZBZBA⋅AZCZCB=BZABC⋅BCZAC⋅CZBCA⋅CAZBA⋅AZCAB⋅ABZCB==αβγ(1-α)(1-β)(1-γ)
adódik, azaz
αβγ=(1-α)(1-β)(1-γ).(1)

Könnyen látható, hogy az AA', BB' és CC' egyenesek által határolt (esetleg elfajuló) háromszög pontosan akkor tartalmazza a Z pontot, ha vagy BA'≤BZA és CB'≤CZB, valamint AC'≤AZC teljesül; vagy akkor, ha BA'≥BZA, CB'≥CZB és AC'≥AZC áll fenn. Ez azt jelenti, hogy
p(Z)=αβγ+(1-α)(1-β)(1-γ)=2αβγ=2(1-α)(1-β)(1-γ),
az utóbbi egyenlőségek (1) miatt teljesülnek. A számtani és mértani közép közti egyenlőtlenségből
p(Z)23=αβγ3≤α+β+γ3,illetvep(Z)23=(1-α)(1-β)(1-γ)3≤3-α-β-γ3
következik, ahonnan
2p(Z)23≤α+β+γ3+3-α-β-γ3=1
alapján p(Z)≤14 adódik. Egyenlőség pedig akkor állhat, ha mindkét számtani és mértani közép közti egyenlőtlenségnél egyenlőség áll, azaz ha α=β=γ teljesül. Ekkor azonban (1) miatt α=β=γ=12, azaz Z az ABC háromszög súlypontja. Könnyen ellenőrizhető, hogy a súlypontra minden fenti becslés csakugyan egyenlőséggel teljesül. Ez pedig azt igazolja, hogy a feladat kérdésére a súlypont a válasz.  □
 
Megjegyzés. A feladat könnyen megoldható a baricentrikus koordináták segítségével. Legyenek tehát α, β, γ az Z baricentrikus koordinátái, azaz Z→=αA→+βB→+γC→, ahol X→ jelöli az X ponthoz tartozó helyvektort és α+β+γ=1. Ekkor a
p(Z)=2⋅αβγ(α+β)(β+γ)(γ+α)
kifejezést kell maximalizálni. Márpedig a számtani és mértani közép közti egyenlőtlenségből
(α+β)(β+γ)(γ+α)≥2αβ⋅2βγ⋅2γα=8αβγ
adódik, ahonnan
p(Z)=2⋅αβγ(α+β)(β+γ)(γ+α)≤2⋅αβγ8αβγ=14
következik, egyenlőség pedig kizárólag α=β=γ esetén áll. A kérdezett valószínűség tehát α=β=γ=13 esetén, azaz a súlypontra maximális.

 
2. Vannak-e olyan f(x) és g(x) valós együtthatós polinomok, amelyekre az f(x)3-g(x)2 polinom elsőfokú?
 
I. megoldás. Megmutatjuk, hogy nincsenek ilyen polinomok. Indirekt bizonyítunk, tegyük fel, hogy
f(x)3-g(x)2=ax+b,ahol  a≠0.(2)
Ez a formula akkor volna jól kezelhető, ha a jobb oldalon teljes négyzet ellentettje állna. Ennek érdekében bevezetjük az y változót, és alkalmazzuk az x=(-y2-b)/a helyettesítést. Ekkor
f(x)=f(-y2-ba)=F(y2),illetveg(x)=G(y2)
teljesül alkalmas F és G polinomokra, ahonnan
F(y2)3=G(y2)2-y2=(G(y2)-y)⋅(G(y2)+y)(3)
adódik. A bal oldali polinom fokszáma 6-tal osztható, ezért G nem lehet konstans. Ha F konstans tagja 0, akkor ugyanez G-re is igaz. Ám ekkor a bal oldalon álló polinom legalacsonyabb fokú tagjának foka 6-tal osztható, míg a jobb oldalon álló esetében ez a fok pontosan 2. Ezért a G polinom nem konstans, de van konstans tagja. A jobb oldali két tényező relatív prím, hiszen ha egy polinom mindkettőt osztja, akkor a különbségüket és az összegüket, a 2y és a 2G(y2) polinomokat is osztja, ám ez utóbbi polinomok relatív prímek, hisz 2G(y2) konstans tagja nem nulla.
A valós együtthatós polinomok körében érvényes a számelmélet alaptétele, ezért (3) jobboldalának mindkét tényezője egy-egy valós együtthatós polinom köbének konstansszorosa. Mivel minden valós konstans előáll valós szám köbeként, azt kapjuk, hogy vannak olyan, valós együtthatós p(y) és q(y) polinomok, amelyekre
p(y)3=G(y2)-y,illetveq(y)3=G(y2)+y(4)
teljesül. Láttuk, hogy G nem konstans. Ezért a (4) két jobb oldalán álló polinom legmagasabb fokú tagja megegyezik és legalább másodfokú. Ugyanez igaz tehát a két bal oldalon álló polinomra is: p(y) és q(y) legmagasabb fokú nemnulla tagja ugyanaz a cyn monom, ahol n≥1. Ekkor azonban a
2y=q(y)3-p(y)3=(q(y)-p(y))⋅(q(y)2+q(y)p(y)+p(y)2)(5)
egyenlőség jobb oldalán a második tényezőben y2n együtthatója 3c2≠0, ezért a jobb oldal nem lehet elsőfokú. A kapott ellentmondás a megoldás elején kimondott állítást bizonyítja.  □
 
II. megoldás. Ismét indirekt bizonyítunk, tegyük fel tehát, hogy
f(x)3=g(x)2+r(x),ahol  r(x)=ax+b  és  a≠0.(6)
Nyilván sem f, sem g nem lehet konstans, ezért degf=2k és degg=3k valamilyen pozitív egész k-ra. Legyen d=gcd(f,g). Ekkor persze d2∣f3-g2=r, ám mivel r elsőfokú, d csak konstans lehet, vagyis f és g egymáshoz relatív prímek. Most (6) mindkét oldalát deriválva az
3f(x)2f'(x)=2g(x)g'(x)+r'(7)
egyenlőséget kapjuk, ahonnan a (6) r'-szereséből kivonva a (7) r-szeresét,
f2(fr'-3f'r)=g(gr'-2g'r)
adódik. A bal oldal osztható azzal az f2 polinommal, amihez a jobb oldalon álló g relatív prím, tehát
f2∣gr'-2g'r.(8)
Ekkor azonban degf2=4k, míg gr'-2g'r foka legfeljebb 3k. Ráadásul ha a g főegyütthatója d, akkor (gr'-2g'r)-ben a 3k-adfokú tag együtthatója
da-6kda=(1-6k)da≠0.
Vagyis a gr'-2g'r polinom nem lehet a nulla polinom, és a foka pontosan 3k.
Tehát a (8) szerint a 4k-adfokú f2 osztója a pontosan 3k-adfokú, nemnulla gr'-2g'r polinomnak, ez pedig lehetetlen.  □
 

Megjegyzések. 1. Vannak olyan nem konstans f és g polinomok, amelyekre f3-g2 másodfokú, például (x2+2)3-(x3+3x)2=3x2+8. Igazolható, hogy ez csak úgy lehetséges, ha egyrészt f és g relatív prímek, másrészt pedig ha a fokszámaik degf=2 és degg=3.
2. A feladat szorosan kapcsolódik az ún. abc-sejtéshez, ami az alábbit mondja ki. Minden pozitív ε-ra van olyan Cε konstans, hogy ha a, b, c relatív prím pozitív egészek és a+b=c, akkor c<Cε⋅rad(abc)1+ε. Itt rad(n) az n radikálját jelöli, azaz az n különböző prímosztóinak szorzatát. (Pl. rad(2016)=42, rad(2017)=2017 és rad(2018)=2018.) Az abc-sejtésből számos nehéz tétel és sejtés következik. Levezethető belőle például a nagy Fermat-tételt általánosító Beal-sejtés gyengítése, miszerint az an+bm=ck egyenletnek csak véges sok olyan megoldása van a pozitív egészek körében, amelyre a, b, c relatív prímek és n, m, k mindegyike legalább 3. Az abc-sejtésre jelenleg nem ismert általánosan elfogadott bizonyítás. Ígéretes fejlemény azonban Mocsizuki Sinicsi japán matematikus 2012-ben publikált 500 oldalas munkája, amelyben egy egészen új elméletet dolgoz ki és bizonyít számos számelméletet érintő sejtést, többek között az abc-sejtést. Mocsizuki elmélete azonban annyira újszerű, hogy még jelenleg is tart annak ellenőrzése. Tekintettel arra, hogy az intenzív munka ellenére még nem találtak benne lényeges hibát, könnyen elképzelhető, hogy a közeli jövőben bejelentik a sejtés megoldását. Ha pedig ez megtörténik, valószínűleg semmi sem mentheti meg a szerzőt egy igen tekintélyes matematikai díjtól, ami persze nem lehet a Fields-érem, hiszen azt 40 év felettiek nem kaphatják.
Ismert és bizonyított azonban az abc-sejtésnek egy polinomos megfelelője, az ún. Mason-tétel. Jelölje rad(f) az f komplex együtthatós polinom különböző irreducibilis faktorainak szorzatát. (Tehát rad(f) foka az f különböző komplex gyökeinek száma.) Legyenek f, g és h olyan komplex együtthatós relatív prím polinomok, amelyek nem mindegyike konstans és f+g=h. Ekkor a Mason-tétel szerint
max(deg(f),deg(g),deg(h))≤deg(rad(fgh))-1.

A Mason-tétel segítségével a kitűzött feladat könnyen megoldható. Tegyük fel tehát, hogy (5) teljesül. A II. megoldásban láttuk, hogy f, g relatív prímek, tehát f3, g2 és r is azok. Nyilván deg(f)=2k, deg(g)=3k alkalmas k pozitív egészre. A Mason-tétel szerint ekkor
6k=max(6k,6k,1)≤deg(rad(f3g2r))-1=deg(rad(fgr))-1≤≤deg(fgr)-1=deg(f)+deg(g)+deg(r)-1=5k,
ami ellentmondás, így (5) nem teljesülhet.

 
3. Egy n×n-es T táblázat mezőibe egy-egy számot írtunk úgy, hogy egyik sorban sem szerepel kétszer ugyanaz a szám. Bizonyítsuk be, hogy át lehet rendezni a T-ben szereplő számokat úgy, hogy az átrendezés utáni T* táblázat minden sorában pontosan ugyanazok a számok álljanak, mint amelyek T megfelelő sorában álltak, de T* semelyik oszlopában se szerepeljen kétszer ugyanaz a szám.
 
I. megoldás. Egy n×n-es táblázat k-dik oszlopának hibája legyen n-d(k), ahol d(k) jelöli a k-dik oszlopbeli különböző számok számát. A táblázat összhibája pedig legyen a táblázatbeli oszlopok hibáinak összege. Azt kell igazolnunk, hogy T sorain belül lehet úgy permutálni az ott álló számokat, hogy az így kapott táblázat összhibája 0 legyen. Az alábbiakban egy olyan eljárást mutatunk, amely tetszőleges pozitív összhibájú táblázat esetén bizonyos sorok alkalmas átrendezésével csökkenti az összhibát. Mivel a szóban forgó összhiba egész szám, ezért e hibacsökkentő lépés véges sokszori alkalmazásával a táblázat összhibája 0-ra csökkenthető, és ezzel a feladat állítása bizonyítást nyer.
Tegyük fel tehát, hogy T-ben ‐ mondjuk ‐ az első oszlop hibája pozitív. Ennek oka, hogy legalább két azonos szám (mondjuk két 1-es) szerepel benne. Mivel T minden sorában legfeljebb egy 1-es szerepel, ezért T-nek lesz olyan oszlopa, amiben nem szerepel 1-es. Az általánosság megszorítása nélkül feltehető, hogy a második oszlop ilyen. Egy G irányított gráfot definiálunk a T táblázat első két oszlopában előforduló számok (mint csúcsok) halmazán úgy, hogy ha valamelyik sorban az első két elem i és j (ebben a sorrendben), akkor G-be behúzunk egy i-ből j-be vezető élt.
Induljunk el az így kapott G gráf 1-es csúcsából, és haladjunk az irányított élek mentén. Két eset lehetséges. Előbb-utóbb vagy egy olyan u (nyelő) csúcsba érkezünk, ahonnan nem vezet ki él vagy egy olyan v csúcsba érünk, ahol már korábban jártunk. Mindkét esetben felcseréljük a bejárt éleknek megfelelő sorok első két elemét. Ezáltal az első esetben az első oszlopban csökken az 1-esek száma, míg a második oszlopban megjelenik egy 1-es, továbbá, a második oszlopból egy, az első oszlopban eddig nem szerepelő u elem kerül át az első oszlopba. Ettől eltekintve az egyes oszlophoz tartozó számhalmazok nem változnak, tehát T összhibája 2-vel csökken. A második esetben az első két oszlophoz tartozó számhalmazok úgy változnak, hogy egy 1-es átkerül az első oszlopból a másodikba, miközben egy ettől különböző, az első oszlopban már eddig is megtalálható v szám átkerül a második oszlopból az elsőbe. Ezáltal az első oszlopban álló számok halmaza nem változik, tehát az első oszlop hibája is annyi marad amennyi volt. Emellett azonban a második oszlop hibája, és ennek megfelelően a táblázat összhibája eggyel csökken. Ezzel a hibacsökkentő lépést leírtuk, a feladat állítását igazoltuk.
 
II. megoldás. Készítsük el azt a GT páros gráfot, amelynek egyik színosztályának s1,s2,...,sn csúcsait a T táblázat sorai, a másik színosztálybeli a1,a2.... csúcsokat pedig a T-ben található számok alkotják. Az si és aj csúcsok között pedig akkor fusson él GT-ben, ha az aj szám előfordul a T táblázat si sorában. Világos, hogy minden si csúcs GT-beli fokszáma pontosan n, míg tetszőleges aj csúcs fokszáma pedig legfeljebb n, hiszen egyfelől minden sorban pontosan n szám áll, másfelől pedig minden szám legfeljebb n-szer (soronként egyszer) fordul elő a T-ben. Kőnig ismert élszínezési tétele szerint tehát GT élei kiszínezhetők az 1,2,...,n színek felhasználásával úgy, hogy a közös végponttal rendelkező élek különböző színt kapjanak.
Ennek a színezésnek a segítségével az alábbi módon rendezzük át a T táblázat sorait. Mivel si-ből GT-ben n különböző színű él indul, ezért ezen élek közül pontosan egy (mondjuk siaj) kapta a k-dik színt. Legyen ekkor aj a T* táblázat vi sorának k-dik eleme. A GT definíciója miatt aj szerepel a T táblázat si sorában, tehát az imént definiált átrendezés valóban végrehajtható a T táblázaton. Mivel a fenti T* minden egyes oszlopában azonos színre színezett éleknek megfelelő számok állnak, ezért T* egyetlen oszlopában sem állhat két egyforma szám. Nekünk pedig éppen ezt kellett igazolunk.
 

Megjegyzések. 1. A feladat ,,hátterét'' a II. megoldás mutatja: voltaképp Kőnig élszínezési tételével egyenértékű a bizonyítandó állítás. A trükk annyi, hogy a táblázat által definiált ,,szokásos'' páros gráf helyett (aholis az oszlopok és a sorok felelnek meg a színosztályoknak, és a táblázat mezői pedig az éleknek), itt az egyik színosztályt a sorok, a másikat pedig a mezőkben álló számok alkotják, az éleket pedig az oszopok segítségével határozzuk meg. Érdemes végiggondolni, hogy mit is jelent a feladat állítása a ,,szokásos'' értelmezés szerint. Azt kell igazolnunk, hogy bárhogy is adunk meg a Kn,n páros gráf A színosztályának minden csúcsához n különböző színt, a gráf n2 éle kiszínezhető úgy, hogy az azonos csúcsból induló élek színe különböző legyen és emellett minden él színe az A-beli végponthoz megadott színek közül kerüljön ki.
2. Dinitz sejtése azt mondja ki, hogy ha egy n×n méretű táblázat mind az n2 mezejéhez tartozik egy-egy n elemű halmaz, akkor kiválasztható ezen halmazoknak egy-egy eleme úgy, hogy azonos sorban vagy oszlopban álló mezőkhöz tartozó halmazokból ne válasszunk azonos elemet. Világos, hogy a sejtésből azonnal következik a feladat állítása, ha hozzárendeljük minden mezőhöz az adott mező sorában álló számokat. Dinitz sejtését Galvin igazolta, mégpedig abban az általánosabb formában, hogy ha egy G véges, páros gráf minden éléhez legalább akkora színlista tartozik, mint a G-beli legnagyobb fokszám, akkor minden élhez úgy választható a listájából egy-egy szín, hogy az így kapott színezésben azonos színű éleknek ne legyen közös végpontja. Érdemes még megemlíteni, hogy nem páros gráfok esetén ugyanez az állítás azzal a változtatással, hogy a színlisták mérete a G gráf élkromatikus száma (ami páros gráfra Kőnig tétele szerint épp a maximális fokszám), nem más, mint az ún. listaszínezési sejtés, amire a mai napig nem ismert bizonyítás.
3. Többen próbálkoztak n szerinti teljes indukció alkalmazásával oly módon, hogy az indukciós lépésben először azt érik el, hogy az utolsó oszlop elemei különbözők legyenek, majd a bal felső (n-1)×(n-1)-es táblázatra alkalmazzák az indukciós feltevést. Sajnos ebben a megközelítésben semmi sem garantálja, hogy az utolsó sor valamelyik (utolsótól különböző eleme) ne egyezzen meg egy másik elemmel ugyanabban az oszlopban. Működik azonban az n szerinti teljes indukció akkor, ha megfelelően általánosítjuk a feladat állítását: azt igazoljuk, hogy amennyiben egy k×n méretű táblázat mind a k sorában csupa különböző szám áll, továbbá egyetlen szám sem fordul elő n-nél többször a táblázatban, akkor lehetséges a sorokon belül úgy permutálni a számokat, hogy minden oszlopban csupa különböző szám álljon. Világos, hogy n=1 esetén ez teljesül. Tegyük fel, hogy n-re már igazoltuk az állítást, és tekintsünk egy k×(n+1) méretű táblázatot. A célunk ekkor az, hogy az utolsó oszlopba úgy rendezzünk be különböző számokat, hogy az első n oszlopra teljesüljön az indukciós feltétel. Ehhez pedig mindössze azt kell elérni, hogy az utolsó oszlopban egyrészt csupa különböző szám álljon, másrészt pedig minden olyan szám, ami pontosan (n+1)-szer fordul elő a táblázatban, szerepeljen az utolsó oszlopban. A ,,szokásos'' páros gráfot definiálva, a Hall-tételből könnyen látható, hogy egyrészt lehetséges az utolsó oszlopba csupa különböző számot becserélni, másrészt pedig lehetséges úgy permutálni a sorokat, hogy minden olyan szám, ami (n+1)-szer szerepel a táblázatban, az utolsó oszlopban is előforduljon. Az indukciós lépés igazolásához azonban a két tulajdonság együttes fennállása szükséges. Ezt pedig a Mendelsohn‐Dulmage tétel biztosítja, amely szerint ha egy G páros gráfban M1 és M2 párosítások (azaz közös végpont nélküli élek halmazai), akkor van olyan M párosítás is G-ben, amely fedi az A színosztály minden M1 által fedett csúcsát és a B színosztály minden M2 által fedett csúcsát.
4. Érdemes végül rámutatni egy másik, a feladathoz szorosan kapcsolódó kutatási területre. A Rota-sejtés azt állítja, hogy ha egy n×n méretű táblázat minden mezejéhez egy-egy Rn-beli vektor tartozik azzal a tulajdonsággal, hogy az egy sorban álló vektorokból bármely Rn-beli vektor előállítható skalárral való szorzás és összeadás segítségével, akkor a táblázat sorain belül lehetséges a vektorokat úgy permutálni, hogy minden oszlopra is teljesüljön, hogy bármely Rn-beli vektor előállítható skalárral való szorzás és összeadás segítségével az adott oszlopban álló vektorokból. A versenyen kitűzött feladat felfogható a Rota-sejtés egy igen speciális eseteként. Hasonlóan a listaszínezési sejtéshez, jelenleg az általános Rota-sejtésre sem ismert bizonyítás.