Cím:	Megoldásvázlatok a 2017/9. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Deák Anna
Füzet:	2018/január, 14 - 20. oldal	PDF  |  MathML
Hivatkozás(ok):	2017/december: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ $A\cup B$ halmaznak $192$ eleme van. $A\cap B$ elemszáma $A$ elemszámának $20\%$-a, $B$ elemszámának $15\%$-a. Hány eleme van az $A$ és a $B$ halmaznak?  (6 pont) $b)$ Egy város felnőtt lakosságának $30\%$-a nyugdíjas. A nyugdíjasok $55\%$-a nő. A férfiaknak $73\%$-a aktív korú (nem nyugdíjas). Bizonyítsuk be, hogy a városban a felnőtt férfiak és nők száma egyenlő.  (5 pont)   Megoldás. $a)$ Legyen az $A\cap B$ halmaz elemszáma $x$, ekkor $A\setminus B$ elemszáma $4x$. Jelölje a $B\setminus A$ halmaz elemszámát $y$. Ekkor $\begin{array}{c}{\displaystyle \frac{x}{x+y}=\frac{1\mathrm{,}5}{10}\mathrm{,}\text{amiből}y=\frac{17}{3}x\mathrm{.}}\end{array}$ Tehát $192=\frac{32}{3}x$, amiből $x=18$, így $A$ elemszáma $90$, míg $B$ elemszáma 120. $b)$ A nyugdíjasoknak $45\%$-a férfi, ez a $30\%$-nak a $45\%$-a, azaz a nyugdíjas férfiak száma a teljes lakosság $13\mathrm{,}5$%-a. Másfelől a férfiak $100-73=27\%$-a nyugdíjas. Így a férfiak $27\%$-a annyi, mint a teljes lakosság $13\mathrm{,}5\%$-a. A férfiak számát $F$-fel, míg a teljes lakosság számát $T$-vel jelölve $0\mathrm{,}27\cdot F=0\mathrm{,}135\cdot T$, ebből $F=0\mathrm{,}5\cdot T$, vagyis a férfiak a teljes lakosság felét teszik ki.   2. $a)$ Oldjuk meg az egyenletet a valós számok halmazán: $3^{2+x}+3^{6-x}=2190$.  (7 pont) $b)$ Legyen az $a_n$ sorozat definíciója: $a_n=8^{n\left(n+1\right)}$. Bizonyítsuk be, hogy a sorozat első $n$ tagjának szorzata $2^{n\left(n+1\right)\left(n+2\right)}$.  (7 pont)   Megoldás. $a)$ $\begin{array}{c}{\displaystyle 9\cdot 3^x+\frac{729}{3^x}=2190.}\end{array}$ $3^x$-t $z$-vel jelölve és az egyenletet rendezve a $\begin{array}{c}{\displaystyle 3z^2-730z+243=0}\end{array}$ egyenlethez jutunk, melynek gyökei $z_1=243$ és $z_2=1/3$. Ebből $x_1=5$ és $x_2=-1$. Mindkét gyök megfelelő, mert ekvivalens átalakításokat végeztünk. $b)$ Az első $n$ tag szorzata $\begin{array}{c}{\displaystyle 8^{1\cdot 2+2\cdot 3+3\cdot 4+\text{...}+n\left(n+1\right)}=2^{3\cdot \left(1\cdot 2+2\cdot 3+3\cdot 4+\text{...}+n\left(n+1\right)\right)}\mathrm{.}}\end{array}$ Mivel az exponenciális függvény kölcsönösen egyértelmű, azt kell bizonyítanunk, hogy $\begin{array}{c}{\displaystyle 3\cdot \left(1\cdot 2+2\cdot 3+3\cdot 4+\text{...}+n\cdot \left(n+1\right)\right)=n\left(n+1\right)\left(n+2\right)\mathrm{.}}\end{array}$ Bizonyítsuk teljes indukcióval: 1. $n=1$ esetén az állítás igaz, mert $3\cdot 1\cdot 2=1\cdot 2\cdot 3$. 2. Tegyük fel, hogy valamilyen $n$-re az állítás igaz. Ekkor $n+1$-re: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 3\cdot \left(1\cdot 2+2\cdot 3+3\cdot 4+\text{...}+n\cdot \left(n+1\right)+\left(n+1\right)\left(n+2\right)\right)=}\hfill \\ \hfill {\displaystyle =}& {\displaystyle 3\cdot \left(1\cdot 2+2\cdot 3+3\cdot 4+\text{...}+n\cdot \left(n+1\right)\right)+3\cdot \left(n+1\right)\left(n+2\right)=}\hfill \\ \hfill {\displaystyle =}& {\displaystyle n\left(n+1\right)\left(n+2\right)+3\cdot \left(n+1\right)\left(n+2\right)=\left(n+1\right)\left(n+2\right)\left(n+3\right)\mathrm{.}}\hfill \end{array}}$   3. 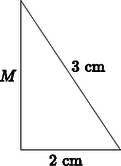$a)$ Egy $10$ egység sugarú körbe az $ABCD$ négyszöget írtuk. A négyszög két átlója ${70}^{\circ }$-os szögben metszi egymást. Az $AC$ átló hossza $20$ egység, és a $CD$ oldallal ${40}^{\circ }$-os szöget zár be. Számítsuk ki a négyszög szögeit.  (6 pont) $b)$ Egy $10$ egység sugarú gömbbe csonkakúpot írunk, melynek alap-, illetve fedőlapja a gömb középpontjától 6 cm, illetve 8 cm távolságra van. (A gömb középpontja a két sík közé esik.) Számítsuk ki a csonkakúp felszínét.  (8 pont)   Megoldás. $a)$ $AC$ átmérő, mert kétszerese a kör sugarának. Thalész tétele szerint $ABC\sphericalangle$ és $ADC\sphericalangle$ derékszög. $ABD\sphericalangle =ACD\sphericalangle ={40}^{\circ }$, mert ugyanahhoz a húrhoz tartozó kerületi szögek. Két jó négyszöget kapunk, az 1. ábra háromszögeinek minden szögét kiszámítva és a megfelelőket összeadva kapjuk, hogy a hiányzó két szög ${80}^{\circ }$ és ${100}^{\circ }$, illetve ${120}^{\circ }$ és ${60}^{\circ }$.   1. ábra   $b)$ Nézzük a gömb és a csonkakúp (forgástengelyén átmenő) síkmetszetét. Pitagorasz tételéből a fedőkör sugara $r=6$ cm, az alapkör sugara $R=8$ cm (2. ábra). Az alkotó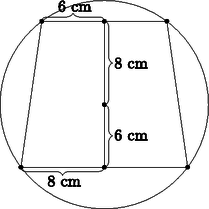: $a^2={14}^2+2^2=200$, ebből $\begin{array}{c}{\displaystyle a=\sqrt[]{200}\approx 14\mathrm{,}14\text{cm}\mathrm{.}}\end{array}$   2. ábra   Az adatokat az $A=\pi \cdot \left[R^2+r^2+\left(R+r\right)a\right]$ képletbe behelyettesítve azt kapjuk, hogy a csonkakúp felszíne $936\mathrm{,}2{\text{cm}}^3$.   4. Elemezzük monotonitás szempontjából a valós számok halmazán értelmezett $f\left(x\right)=x^4-8x^3+13\mathrm{,}5x^2+10$ függvényt, és adjuk meg lokális szélsőértékeit.  (12 pont)   Megoldás. A függvény deriváltja $f\text{'}\left(x\right)=4x^3-24x^2+27x=x\cdot \left(4x^2-24x+27\right)$. A zárójelben szereplő másodfokú kifejezés gyökei 1,5 és 4,5, így grafikonja vázlatosan a 3. ábrán látható.   3. ábra   Előjele a $\left]-\infty ;1\mathrm{,}5\right]$ és a $\left]4\mathrm{,}5;\infty ;\right]$ intervallumon pozitív, az $\left]1\mathrm{,}5;4\mathrm{,}5\right]$ intervallumon negatív. Ezt $x$-szel szorozva kapjuk $f\text{'}\left(x\right)$-et, ami ezek szerint a 0, 1,5 és 4,5 helyeken vesz fel 0 értéket, továbbá ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mo stretchy="false">-</mo><mo>∞</mo><mi>;</mi><mn>0</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon negatív, }}\hfill \\ \hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>0</mn><mi>;</mi><mn>1</mn><mn>,</mn><mn>5</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon pozitív, }}\hfill \\ \hfill {\displaystyle \text{ az}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>1</mn><mn>,</mn><mn>5</mn><mi>;</mi><mn>4</mn><mn>,</mn><mn>5</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon negatív,}}\hfill \\ \hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>4</mn><mn>,</mn><mn>5</mn><mi>;</mi><mo>∞</mo></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon pozitív. }}\hfill \end{array}}$ Fentiek alapján az $f\left(x\right)$ függvény ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mo stretchy="false">-</mo><mo>∞</mo><mi>;</mi><mn>0</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon szigorúan monoton csökken,}}\hfill \\ \hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>0</mn><mi>;</mi><mn>1</mn><mn>,</mn><mn>5</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon szigorúan monoton nő, }}\hfill \\ \hfill {\displaystyle \text{ az}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>1</mn><mn>,</mn><mn>5</mn><mi>;</mi><mn>4</mn><mn>,</mn><mn>5</mn></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon szigorúan monoton csökken,}}\hfill \\ \hfill {\displaystyle \text{ a}}& {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mo fence="true" stretchy="true">]</mo><mrow><mn>4</mn><mn>,</mn><mn>5</mn><mi>;</mi><mo>∞</mo></mrow><mo fence="true" stretchy="true">[</mo></mrow></math>}}\hfill & {\displaystyle \text{intervallumon szigorúan monoton nő. }}\hfill \end{array}}$ Ezekből következik, hogy 0-ban és 4,5-ben a függvénynek lokális minimuma, 1,5-ben lokális maximuma van. Ezek értéke: $f\left(0\right)=10$; $f\left(1\mathrm{,}5\right)=18\mathrm{,}4375$; $f\left(4\mathrm{,}5\right)=-35\mathrm{,}5625$. Grafikonja vázlatosan a 4. ábrán látható.   4. ábra     II. rész     5. Egy dobókockához hasonlóan használható fajáték alakja két egybevágó, alapjuknál egymáshoz illesztett szabályos hatoldalú gúla, amelyeknek alapéle 2 cm, oldaléle 3 cm. $a)$ Számítsuk ki a test tömegét (grammban kifejezve), ha anyagának sűrűsége 430 kg/m${}^3$.  (7 pont) $b)$ A test lapjai közül négy piros, a többi fekete. A piros dobás jelent szerencsét a társasjátékban. Ha tíz játékos dob egyszerre egy-egy ilyen testtel, mekkora a valószínűsége, hogy a játékosoknak pontosan a fele dob pirosat?  (3 pont)     $c)$ A játék során a tíz játékos összesen öt alkalommal dobott egyszerre. Mindegyik alkalommal feljegyezték a piros dobások számát. Mind az öt esetben a játékosok kevesebb, mint fele dobott pirosat, de olyan nem fordult elő, hogy egyiküknek sem volt szerencséje. Mi volt az öt feljegyzett szám, ha átlaguk 1,6 és szórásuk 0,8? (A számok sorrendje nem kérdés.)  (6 pont)   Megoldás. $a)$ A gúla alapterülete $T=6\cdot 2^2\cdot \frac{\sqrt[]{3}}{4}{\text{cm}}^2$, magassága $M=\sqrt[]{5}$ cm. Térfogata $2\cdot \frac{TM}{3}\approx 15\mathrm{,}49{\text{cm}}^3$, sűrűsége 0,43 g/cm${}^3$, ebből a tömege $\approx 0\mathrm{,}66$ g.     $b)$ A piros dobás valószínűsége $\frac{1}{3}$, így a keresett valószínűség: $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{10}{5}\right){\left(\frac{1}{3}\right)}^5\cdot {\left(\frac{2}{3}\right)}^5\approx 0\mathrm{,}137.}\end{array}$ $c)$ Mind az öt szám 1 és 4 között van, és az egyik biztosan 1-es. A másik négy szám összegét $x$-szel jelölve $\frac{1+x}{5}=\mathrm{1,6}$, amiből $x=7$. A másik négy szám lehetséges értékei növekvő sorrendben: $1$, $1$, $1$, $4$; $1$, $1$, $2$, $3$ vagy $1$, $2$, $2$, $2$. Ezek közül csak a második esetben lesz a szórás 0,8. Tehát az öt feljegyzett szám az 1, 1, 1, 2, 3 volt.   6. Az ábrán látható huszonöt kör mindegyikét fehérre vagy feketére színezzük. (Az ábra rögzített, a mozgatással egymásba vihető színezéseket nem tekintjük azonosnak.)     $a)$ Hány olyan színezés lehetséges, amelyben több a fekete kör, mint a fehér?  (3 pont) $b)$ Hány olyan színezés lehetséges, amely szimmetrikus az ábra vízszintes vagy függőleges tengelyére?  (6 pont) $c)$ Hány olyan színezés lehetséges, amelyben pontosan $7$ kör fekete, és szimmetrikus az ábra függőleges tengelyére?  (7 pont)   Megoldás. $a)$ A 25 kört összesen $2^{25}$-féleképp színezhetjük. Mivel nem lehet egyenlő a fekete és fehér körök száma, és ugyanannyi olyan eset van, amelyben több a fehér, mint amelyben több a fekete, az utóbbi lehetőségek száma az összesnek a fele, azaz $2^{24}$. $b)$ Tekintsük először a függőleges tengelyre szimmetrikus megoldásokat. Szabadon színezhetjük a tengely köreit és a tőle balra eső köröket ‐ a jobboldali körök színét ez már meghatározza. Mivel 15 körről dönthetünk szabadon, a lehetőségek száma $2^{15}$. Ugyanennyi olyan színezés van, ami a vízszintes tengelyre szimmetrikus. Azok a színezések, amelyek mindkét tengelyre szimmetrikusak, úgy állíthatók elő, hogy szabadon színezzük a valamelyik sarokban lévő $3\times 3$-as részt, majd ebből már következik a többi kör színe ‐ ez tehát $2^9$ lehetőség. Összesítve: a legalább az egyik tengelyre szimmetrikus megoldások száma $2\cdot 2^{15}-2^9$. $c)$ A tengelyen kívül eső fekete körök egyenlően oszlanak meg a bal- és a jobboldalon, ezért a tengelyen páratlan számú fekete körnek kell lennie. Középen 1, baloldalt 3 fekete kör: $5\cdot \left(\genfrac{}{}{0ex}{}{10}{3}\right)=600$ lehetőség. Középen 3, baloldalt 2 fekete kör: $\left(\genfrac{}{}{0ex}{}{5}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{10}{2}\right)=450$ lehetőség. Középen 5, baloldalt 1 fekete kör: $1\cdot 10=10$ lehetőség. Összesen tehát 1060 ilyen színezés lehetséges.   7. Az $ABC$ derékszögű háromszög befogói $AC=7$ egység, $BC=3$ egység. A háromszögbe az ábrán látható módon négyzetet írtunk.     $a)$ Milyen hosszú a négyzet oldala?  (4 pont) Az $AFE$ derékszögű háromszögbe ugyanilyen módon újabb négyzetet írunk, majd az ekkor keletkezett újabb, $A$ csúccsal rendelkező derékszögű háromszögbe újabb négyzetet stb. $b)$ Milyen hosszú a hatodik négyzet oldala?  (4 pont) $c)$ Tovább folytatva az eljárást, összesen hány négyzet oldala lesz nagyobb, mint 0,0001?  (4 pont) $d)$ Mekkora a négyzetek ,,fölött'' ($DBE$ mintájára) keletkező végtelen sok derékszögű háromszög területének összege?  (4 pont)   Megoldás. $a)$ Az 5. ábrán látható derékszögű háromszögek hasonlóak, mert megfelelő szögeik egyenlők. A négyzet oldalát $x$-szel jelölve $\left(3-x\right):x=3:7$, ebből $x=2\m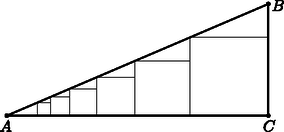athrm{,}1$.   5. ábra   $b)$ Az $AFE$ háromszögbe írható négyzet oldala úgy aránylik $EF$-hez, mint az első négyzet oldala $BC$-hez, azaz $2\mathrm{,}1:3=0\mathrm{,}7.$ Hasonlóképpen mindegyik négyzet oldala 0,7-szerese az előzőnek. A hatodik négyzet oldala tehát $3\cdot 0\mathrm{,}{7}^6\approx 0\mathrm{,}353$. $c)$ A $3\cdot 0\mathrm{,}{7}^n>0\mathrm{,}0001$ egyenlőtlenség megoldása $n<\text{lg}\left(0\mathrm{,}0001/3\right):\text{lg}0\mathrm{,}7\approx 28\mathrm{,}9$. Vagyis 28 négyzet oldala nagyobb 0,0001-nél. $d)$ A $DBE$ háromszög területe $2\mathrm{,}1\cdot 0\mathrm{,}9:2=0\mathrm{,}945$. A háromszögek területe végtelen mértani sort alkot, melynek első tagja 0,945, hányadosa 0,49 (a hasonlóság arányának négyzete, 6. ábra). A mértani sor összegképletéből az együttes terület $\approx \mathrm{1,85}$ egység. 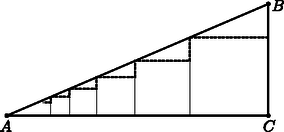  6. ábra     8. $a)$ Egy várfal nyugat-keleti irányú egyenes szakaszán négy kisméretű bástya áll, sorrendben $A$, $B$, $C$ és $D$. Az $A$ és a $D$ bástya az egyenes fal két végén helyezkedik el. Egy, az $A$ bástyától pontosan északi irányban található megfigyelőpontból az $AB$ szakasz ${31}^{\circ }$-os, a $BC$ szakasz ${17}^{\circ }$-os, a $CD$ szakasz pedig ${14}^{\circ }$-os szögben látszik. A bástyák közötti távolságok közül csak a $BC$ távolságot ismerjük, ez 200 méter. Mekkora az $AB$ és a $CD$ távolság? Készítsünk ábrát. Az eredményeket 10 m pontossággal adjuk meg.  (7 pont) $b)$ Egy egyenlőszárú háromszög szárhoz tartozó súlyvonala az alappal ${20}^{\circ }$-os szöget zár be. Mekkorák a háromszög szögei?  (9 pont)   Megoldás. A 7. ábra jelöléseit használva $x=a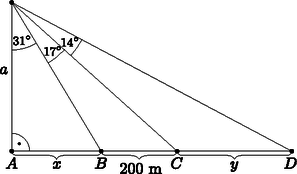\cdot \text{tg}{31}^{\circ }$, $x+200=a\cdot \text{tg}{48}^{\circ }$.   7. ábra   Az egyenletrendszert megoldva $a=392\mathrm{,}3$ m és $x=235\mathrm{,}7$ m adódik. $\begin{array}{c}{\displaystyle 235\mathrm{,}7+200+y=392\mathrm{,}3\text{tg}{62}^{\circ }\mathrm{,}}\end{array}$ ebből $y=302\mathrm{,}1\text{m}$. Tehát $AB\approx 240$ méter, $CD\approx 300$ méter. $b)$ A 8. ábrára a szinusztételt felírva: $\begin{array}{c}{\displaystyle \frac{\text{sin}\left(\alpha +{20}^{\circ }\right)}{\text{sin}\left(\alpha -{20}^{\circ }\right)}=\frac{2}{1}\mathrm{.}}\end{array}$ Rendezve és addíciós tételeket alkalmazva: $\begin{array}{c}{\displaystyle \text{sin}\alpha \text{cos}{20}^{\circ }+\text{cos}\alpha \text{sin}{20}^{\circ }=2\left(\text{sin}\alpha \text{cos}{20}^{\circ }-\text{cos}\alpha \text{sin}{20}^{\circ }\right)\mathrm{.}}\end{array}$ Rendezve, majd kihasználva, hogy most $\text{cos}\alpha \ne 0$: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3\text{cos}\alpha \text{sin}{20}^{\circ }}& {\displaystyle =\text{sin}\alpha \text{cos}{20}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle 3\text{tg}{20}^{\circ }}& {\displaystyle =\text{tg}\alpha \mathrm{.}}\hfill \end{array}}$ Ebből $\text{tg}\alpha =1\mathrm{,}092$, $\alpha =47\mathrm{,}{52}^{\circ }$ és ${180}^{\circ }-2\alpha =84\mathrm{,}{96}^{\circ }$.   8. ábra     9. Két, véletlenszám-generátor segítségével előállított $0$ és $10$ közötti számot jelöljünk $x$-szel és $y$-nal. Adjuk meg, mekkora az alábbi események valószínűsége: $\begin{array}{c}{\displaystyle A:x+y\le 8;B:x^2+y^2+49\le 10\left(x+y\right);C:20y\ge x^2\mathrm{.}}\end{array}$ (16 pont)   Megoldás. Tekintsük az $\left(x;y\right)$ számpárhoz tartozó pontot a derékszögű koordinátarendszerben. Ez a pont a koordinátatengelyek, valamint az $x=10$ és $y=10$ egyenesek által határolt négyzet valamelyik pontja. Mindegyik eseménynek megfeleltetjük a hozzá tartozó számpárokkal jelölt pontok halmazát. Az események valószínűsége kiszámítható, mint ezen területtel rendelkező alakzatok és a négyzet területének hányadosa (geometriai valószínűség.) A négyzet területe 100 egység. Az $A$ esemény akkor teljesül, ha $y\le -x+8$, ez pedig a négyzet pontjai közül a sötétre színezett háromszög pontjaira igaz (9. ábra). A háromszög területe 2 egység, ebből az $A$ esemény valószínűsége 0,32.   9. ábra   A $B$ eseményhez tartozó egyenlőtlenséget átrendezve az ${\left(x-5\right)}^2+{\left(y-5\right)}^2\le 1$ egyenlőtlenséghez jutunk. Ennek pedig annak a körlemeznek a pontjai tesznek eleget, melynek sugara 1, középpontja az $\left(5;5\right)$ pont (10. ábra). A kör területe $\pi$, a valószínűség $\pi /100\appr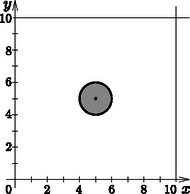ox 0\mathrm{,}0314$.   10. ábra   A $C$ esemény feltétele átrendezve $y\ge \frac{x^2}{20}$. $C$ komplementere az $y<\frac{x^2}{20}$ egyenlőtlenségnek megfelelő ponthalmaz, vagyis az $f\left(x\right)=\frac{x^2}{20}$ függvény grafikonja alatti terület a $\left[0;10\right]$ intervallumon (11. ábra). (Ez a síkidom teljes egészében a négyzetben van, mert a függvény maximuma ezen az intervallumon $\frac{{10}^2}{2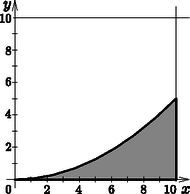0}=5<10$.)   11. ábra   A grafikon alatti terület $\begin{array}{c}{\displaystyle \underset{0}{\overset{10}{\int }}\frac{x^2}{20}\text{d}x=\frac{50}{3}\approx 16\mathrm{,}\mathrm{67,}}\end{array}$ így $C$ komplementerének valószínűsége 0,1667. Ebből $C$ valószínűsége 0,8333. (Megjegyzés: ,,a 0 és 10 közötti szám'' kifejezés nem pontos, nem tudjuk, hogy a határok beleértendők-e. Ennek azonban a terület szempontjából nincs jelentősége.)