Cím:	Gyakorló feladatsor emelt szintű matematika érettségire
Szerző(k):	Varga Péter
Füzet:	2018/január, 11 - 14. oldal	PDF  |  MathML
Hivatkozás(ok):	2018/február: Megoldásvázlatok a 2018/1. sz. emelt szintű matematika gyakorló feladatsorhoz

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán az alábbi egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 4\cdot 2^x+5^y}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle 8\cdot 2^x+3\cdot 5^y}& {\displaystyle =5.}\hfill \end{array}}$  (5 pont) $b)$ Oldjuk meg a $\left[\pi ;2\pi \right]$ intervallumon az alábbi egyenletet: 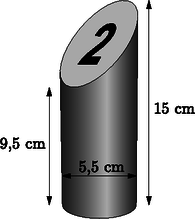$\begin{array}{c}{\displaystyle 3\cdot \text{tg}{}^{2}x-2\sqrt[]{3}\cdot \text{tg}x-3=0.}\end{array}$  (5 pont)   2. A Mölkky egy finn ügyességi játék, amit tizenkét darab fabábuval játszanak. A bábukat 5,5 cm átmérőjű, 15 cm magas egyenes körhenger alakú fából készítik úgy, hogy a henger tetejét az 1. ábrán látható módon ${45}^{\circ }$-os szögben levágják, majd a bábuk tetejére 1‐12-ig sorszámokat rajzolnak.   1. ábra   $a)$ Mekkora egy, a játékhoz használt fabábu térfogata?  (4 pont) A játék kezdetén a bábukat a 2. ábrán látható elrendezésben egy keret segítségével szorosan egymás mellé illesztik, hogy azok érintsék egymást.   2. ábra   $b)$ Mekkora a keret kerülete?  (4 pont) A játék elején a játékosok egy dobófával (Mölkky-vel) próbálják feldönteni a keretben elhelyezkedő tizenkét számozott fabábut. A keretet a dobás előtt leveszik a bábukról. Az egymásra vagy a dobófára támaszkodó bábuk nem számítanak feldőltnek, a szabályosan feldőlt bábunak párhuzamosnak kell lennie a talajjal. Ennek következtében bármilyen kombinációban fel lehet dönteni a bábukat. $c)$ Hányféleképpen lehet egy dobásból három bábut feldönteni úgy, hogy a feldöntött bábukon szereplő számok szorzata négyzetszám legyen?  (5 pont)   3. Adott a derékszögű koordináta-rendszerben két pont: $A\left(1;-2\right)$ és $B\left(3;12\right)$. $a)$ Határozzuk meg az $x$ tengely azon $P$ pontjának koordinátáit, melyre az $ABP$ háromszög egyenlő szárú.  (7 pont) $b)$ Számítsuk ki, hogy az $x$ tengely melyik pontjából látható derékszögben az $AB$ szakasz.  (7 pont)   4. A 3. ábrán egy négyemeletes, 60 cm magas esküvői torta látható, melynek szintjei különböző magasságú és sugarú egyenes hengerek. Az egyes szintek magasságainak hosszai mértani sorozatot alkotnak. $a)$ Milyen magasak az egyes emeletek, ha a legfelső szint 4 cm magas, és a többi szint magasságának mérőszáma is egész szám?  (9 pont) 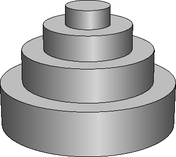  3. ábra   Az esküvői torta 16 cm átmérőjű, 4 cm magas legfelső szintjét a 4. ábrán látható módon díszítéssel látják el.   4. ábra   $b)$ Milyen hosszú a legfelső szintre tekert díszítőcsík, ha a szélességétől eltekintünk?  (5 pont)   II. rész     5. Adott a valós számok halmazán értelmezett $f$ és $g$ függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=5-2x\text{és}g\left(x\right)=2x^2-3x+1.}\end{array}$ $a)$ Adjuk meg a $g\circ f$ függvény zérushelyeit.  (4 pont) $b)$ Számítsuk ki a $\underset{-1}{\overset{1}{{\displaystyle \int }}}f\left(x\right)\text{d}x-\underset{-1}{\overset{1}{\int }}\left(g\left(x\right)+1\right)\text{d}x$ határozott integrált.  (4 pont) $c)$ Írjuk fel a $g$ függvény $f$ függvényre merőleges érintőjének egyenletét.  (8 pont)   6. $a)$ Egy 6 pontú fagráfban a csúcsok fokszámainak terjedelme 2, módusza 1. Hány ilyen különböző 6 pontú fagráf létezik, ha csúcsaikat nem különböztetjük meg egymástól?  (8 pont) $b)$ Hány csúcsa van annak a fagráfnak, amelyben az össze nem kötött pontpárok száma kétszerese az élek számának?  (8 pont)   7. Egy iskolai büfé italautomatájában hétféle rostos üdítő, kétféle ásványvíz és háromféle szénsavas frissítő kapható, mindegyikből pontosan 8 db. $a)$ Hányféle sorrendben vehet ki Emese mindegyik rostos üdítőből pontosan egyet?  (2 pont) $b)$ Hányféleképpen választhat ki Emese 3 db innivalót tetszőleges összeállításban, ha az automatában lévő összes üdítőt különbözőnek tekintjük?  (5 pont) Az italautomaták elég gyakran elromlanak. Egy italautomatákat szervizelő cégnél 0,05 annak a valószínűsége, hogy egy adott napon nincs javítanivaló; 0,2, hogy pontosan egy; 0,6, hogy pontosan két javítanivaló automata van. $c)$ Mekkora annak a valószínűsége, hogy öt egymást követő munkanapon nincs javítanivaló?  (3 pont) $d)$ Mekkora annak a valószínűsége, hogy három nap alatt összesen két gépet kell megjavítaniuk?  (6 pont)   8. Egy egyetem gólyatáborában két csoport szkanderbajnokságot játszik egymással. Azért, hogy felmérjék az erőviszonyokat, először a két csoporton belül mindenki mindenkivel egyszer játszik, majd ezt követően a csoportok tagjai megmérkőznek a másik csoport tagjaival. A játék során a csoportokban összesen 144, míg a csoportok között 156 megmérettetésre kerül sor. $a)$ Hányan vannak az egyik, és hányan a másik csoportban?  (9 pont) A bajnokság megkezdése előtt minden versenyző kap egy sorszámot. $b)$ Botond azt állítja, hogy az egyjegyű sorszámot kapott versenyzők közül ki lehet választani hatot úgy, hogy bárhogy párosítjuk őket, a párokban szereplő versenyzők sorszámainak összege három különböző szám lesz. Igaza van-e?  (7 pont)   9. Egy szabályos háromszög alakú céltábla oldalait $n$ $(n>1$, $n\in \text{N})$ egyenlő részre osztottuk. Ezután az osztópontokon át a háromszög oldalaival párhuzamosan szakaszokat húztunk, melynek végpontjai a megfelelő osztópontok. Az így keletkező egybevágó szabályos kisháromszögeket balról jobbra, egyesével, felváltva feketére és fehérre színezzük úgy, hogy minden sorban az első kisháromszög fekete. $a)$ Mekkora annak a valószínűsége, hogy a céltáblára egyetlen lövést leadva, az fekete mezőt talál el, feltéve, hogy a lövés eltalálja a céltáblát?  (9 pont) $b)$ Határozzuk meg $a$ és $b$ értékét, ha tudjuk, hogy a kapott $p$ valószínűségre minden $n>1$ egész esetén teljesül, hogy $a<p\le b$, ahol $a$ a lehető legnagyobb, $b$ pedig a lehető legkisebb ilyen szám?  (7 pont)