Cím:	Megoldásvázlatok a 2017/8. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Számadó László
Füzet:	2017/december, 524 - 534. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Oldjuk meg a valós számok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle \text{lg}x-\left(1-\text{lg}{}^{2}x\right)=-1.}\end{array}$ $b)$ Igazoljuk, hogy a következő egyenletnek nincs valós megoldása: $\begin{array}{c}{\displaystyle |\text{sin}{}^{2}x-\text{cos}x|=-x^2\mathrm{.}}\end{array}$  (11 pont)   Megoldás. $a)$ Az egyenlet értelmezési tartománya: $x>0$. A zárójel felbontása és az egyenlet rendezése után kapjuk: $\text{lg}{}^{2}x+\text{lg}x=0$. Vagyis két eset van: I. Ha $\text{lg}x=0$, akkor $x=1$. II. Ha $\text{lg}x=-1$, akkor $x=\frac{1}{10}$. A kapott értékek benne vannak az értelmezési tartományban, ezért mindkettő megoldása az egyenletnek. $b)$ Az egyenlet bal oldala minden valós $x$ esetén nemnegatív, az egyenlet jobb oldala pedig nempozitív értékeket vesz fel. Megoldás abban az esetben lehetne, ha mindkét oldal értéke 0 lenne. A jobb oldal helyettesítési értéke csak $x=0$ esetén lesz 0. Ebben az esetben a bal oldal helyettesítési értéke: $|\text{sin}{}^{2}0-\text{cos}0|=|0-1|=1$. Vagyis a két oldal értéke nem egyenlő, valóban nincs valós megoldása az egyenletnek.   2. Adott a derékszögű koordináta-rendszerben három pont: $A\left(4;7\right)$, $B\left(-6;-4\right)$, $C\left(2;-3\right)$. $a)$ Számítsuk ki az $ABCD$ paralelogramma $AC$ és $BD$ átlóegyenesének hajlásszögét. $b)$ Igazoljuk, hogy az $ABCD$ paralelogramma területének mérőszáma egész szám.  (12 pont)   Megoldás. $a)$ I. megoldás. A paralelogramma $K$ középpontja az $AC$ szakasz felezőpontja lesz. A megadott koordináták alapján: $K\left(3;2\right)$. A két átlóegyenes azonos a $BKC$ háromszög $KB$ és $KC$ oldalegyenesével, ezért meghatározzuk a $BKC$ háromszög $K$ csúcsnál lévő belső szögét. Mindhárom csúcs koordinátáját ismerjük, ezért kiszámolhatjuk az oldalak hosszát, majd koszinusztétellel megkapjuk a keresett $\phi$ szöget: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle KB}& {\displaystyle =\sqrt[]{{\left(-6-3\right)}^2+{\left(-4-2\right)}^2}=\sqrt[]{117}=3\sqrt[]{13}\mathrm{,}}\hfill \\ \hfill {\displaystyle KC}& {\displaystyle =\sqrt[]{{\left(2-3\right)}^2+{\left(-3-2\right)}^2}=\sqrt[]{26}\mathrm{,}}\hfill \\ \hfill {\displaystyle BC}& {\displaystyle =\sqrt[]{{\left(-6-2\right)}^2+{\left(-4+3\right)}^2}=\sqrt[]{65}\mathrm{.}}\hfill \end{array}}$ Koszinusztétel a $BKC$ háromszögben: $\begin{array}{c}{\displaystyle 65=117+26-2\cdot 3\sqrt[]{13}\cdot \sqrt[]{26}\cdot \text{cos}\phi \mathrm{,}65=143-78\sqrt[]{2}\cdot \text{cos}\phi \mathrm{,}\text{cos}\phi =\frac{\sqrt[]{2}}{2}\mathrm{.}}\end{array}$ Vagyis a $BKC$ háromszögben a $K$ csúcsnál lévő szög ${45}^{\circ }$. Ez azt jelenti, hogy az $ABCD$ paralelogramma $AC$ és $BD$ átlóegyenesének hajlásszöge ${45}^{\circ }$. II. megoldás. A $K$ pont koordinátái: $K\left(3;2\right)$. Ebből $\overrightarrow{KB}\left(-9;-6\right)$ és $\overrightarrow{KC}\left(-1;-5\right)$. A két vektor skaláris szorzatát kétféleképpen felírva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \overrightarrow{KB}\cdot \overrightarrow{KC}}& {\displaystyle =\left(-9\right)\cdot \left(-1\right)+\left(-6\right)\cdot \left(-5\right)=\mathrm{39,}}\hfill \\ \hfill {\displaystyle \overrightarrow{KB}\cdot \overrightarrow{KC}}& {\displaystyle =|\overrightarrow{KB}|\cdot |\overrightarrow{KC}|\cdot \text{cos}\phi =\sqrt[]{81+36}\cdot \sqrt[]{1+25}\cdot \text{cos}\phi \mathrm{.}}\hfill \end{array}}$ A két egyenlet jobb oldala egyenlő: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 39}& {\displaystyle =\sqrt[]{117}\cdot \sqrt[]{26}\cdot \text{cos}\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{\sqrt[]{2}}{2}}& {\displaystyle =\text{cos}\phi \mathrm{.}}\hfill \end{array}}$ Mivel $0\le \phi <{180}^{\circ }$, ezért ebből $\phi ={45}^{\circ }$ következik. $b)$ A $BD$ átlójú, a tengelyekkel párhuzamos oldalú $BPDQ$ téglalap lefedi az $ABCD$ paralelogrammát. A $BPDQ$ téglalap területéből kivonjuk a fölösleges síkidomok területét, hogy megkapjuk az $ABCD$ paralelogramma területét. A $BD$ átlónak is $K$ a felezőpontja, ezért $B$ és $K$ koordinátáinak ismeretében: $D\left(12;8\right)$. A $B$ és $D$ pontok koordinátáiból meghatározható a $BPDQ$ téglalap oldalainak hossza: $BP=18$, $DP=12$. A $BPDQ$ téglalap területe: 216. A fölösleges síkidomok: a $BC$ átfogójú derékszögű háromszög kétszer, a $DC$ átfogójú derékszögű háromszög kétszer, és a $CP$ átlójú téglalap kétszer. Ezeknek a síkidomoknak az oldalai párhuzamosak a tengelyekkel, az ismert koordináták segítségével a szükséges oldalhosszak is megvannak. Vagyis az $ABCD$ paralelogramma területe: $\begin{array}{c}{\displaystyle 216-2\cdot \frac{8\cdot 1}{2}-2\cdot \frac{10\cdot 11}{2}-2\cdot 10\cdot 1=78.}\end{array}$ Az $ABCD$ paralelogramma területének mérőszáma valóban egész szám.   Megjegyzés. Mivel az $a)$ részben az átlók hajlásszögét pontosan határoztuk meg, ezért az igazoláshoz azt is felhasználhatjuk. Az $ABCD$ paralelogramma területe a $BKC$ háromszög területének négyszeresével egyenlő (hiszen a paralelogrammákat az átlóik négy egyenlő területű háromszögre vágják). A $BKC$ háromszögben $KB=3\sqrt[]{13}$, $KC=\sqrt[]{26}$ és $\phi ={45}^{\circ }$, ezért a területe: $\begin{array}{c}{\displaystyle \frac{3\sqrt[]{13}\cdot \sqrt[]{26}\cdot \frac{\sqrt[]{2}}{2}}{2}=\frac{39}{2}\mathrm{.}}\end{array}$ Ennek négyszerese 78, vagyis a keresett terület mérőszáma valóban egész szám.   3. Egy pékségben az öt legnépszerűbb péksütemény az eladási adatok alapján sorrendben: I. sós négyes, II. rozsos zsömle, III. sajtos rúd, IV. óriás kifli, V. kenyérlángos. Az ezekből eladott mennyiség átlaga és mediánja is tegnap 122 db volt, az öt darabszám egyetlen módusza pedig $114$. Az egyik termékből átlagos mennyiséget adtak el, az öt adat terjedelme pedig $22$. $a)$ Adjuk meg az egyes péksütemények relatív gyakoriságát három tizedesjegy pontossággal. $b)$ Mekkora a darabszámok szórása? $c)$ Ma nyitás után az első hat vásárló mindegyike vásárolt a fenti péksütemények közül egyet. Hányféleképpen tehették ezt meg, ha a vásárlásuk után mindegyik termékből fogyott legalább egy darab?  (14 pont)   Megoldás. $a)$ Mivel a felsorolás az eladási adatok sorrendjében történt, és a darabszámok mediánja 122, ezért sajtos rúdból 122 darabot adtak el tegnap. Az öt darabszám egyetlen módusza 114. Ez azt jelenti, hogy pontosan két olyan termék van, amelyből 114 darabot adtak el. Ezek csakis a negyedik és ötödik helyen állók lehetnek. Ezek alapján tudjuk, hogy óriás kifliből és kenyérlángosból is 114 darab fogyott tegnap. Az öt adat terjedelme 22, vagyis az első helyen szereplő sós négyes darabszáma 22-vel több, mint a kenyérlángosé, azaz 136 db. Az öt adat átlagát is ismerjük, így felírhatjuk a következő egyenletet: $\begin{array}{c}{\displaystyle \frac{136+x+122+114+114}{5}=\mathrm{122,}}\end{array}$ amiből $x=124$ adódik. Vagyis rozsos zsömléből 124 darabot adtak el. Az öt darabszám, azaz a termékek gyakorisága sorrendben: 136, 124, 122, 114, 114. Ezek összege: $5\cdot 122=610$. A gyakoriságokat 610-zel osztva megkapjuk a relatív gyakoriságokat. Ezek a következő táblázatban láthatók három tizedesjegy pontossággal:   ${\displaystyle \begin{array}{|cccccc|}\hline {\displaystyle \text{Termék neve}}\hfill & \hfill {\displaystyle \text{Sós}}\hfill & \hfill {\displaystyle \text{Rozsos}}\hfill & \hfill {\displaystyle \text{Sajtos}}\hfill & \hfill {\displaystyle \text{Óriás}}\hfill & \hfill {\displaystyle \text{Kenyér- }}\hfill \\ {\displaystyle }\hfill & \hfill {\displaystyle \text{négyes}}\hfill & \hfill {\displaystyle \text{zsömle}}\hfill & \hfill {\displaystyle \text{rúd}}\hfill & \hfill {\displaystyle \text{kifli}}\hfill & \hfill {\displaystyle \text{lángos }}\hfill \\ {\displaystyle \text{Relatív gyakoriság}}\hfill & \hfill {\displaystyle \text{ 0,223}}\hfill & \hfill {\displaystyle \text{ 0,203}}\hfill & \hfill {\displaystyle \text{ 0,2}}\hfill & \hfill {\displaystyle \text{ 0,187}}\hfill & \hfill {\displaystyle \text{0,187 }}\hfill \\ \hline\end{array}}$   $b)$ Adott volt az adatok átlaga: 122, ismerjük a gyakoriságokat: 136, 124, 122, 114, 114. Ezek alapján a szórás: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \sqrt[]{\frac{{\left(136-122\right)}^2+{\left(124-122\right)}^2+{\left(122-122\right)}^2+{\left(114-122\right)}^2+{\left(114-122\right)}^2}{5}}=}\hfill \\ \hfill {\displaystyle =\sqrt[]{\frac{328}{5}}\approx 8\mathrm{,}1.}\hfill \end{array}}$ $c)$ Valamelyik termékből kettőnek kellett elfogynia. Rögzítsük ilyen szempontból az egyik péksüteményt, ebben az esetben hat termék sorba rendezéséről van szó, amelyek között kettő egyforma: $P_6^2=\frac{6!}{2}=360$. Természetesen az öt közül bármelyik lehet az, amelyikből kettőt adtak el, ezért a végeredményt az előző darabszám ötszöröse adja. Az összes lehetőség száma: 1800.   4. Két téglalap alakú grafikáról tudjuk, hogy mindkettőnek 65 cm az átlója. Az egyik oldalainak aránya $3:4$, a másiknak pedig $5:12$. $a)$ Melyiknek nagyobb és mennyivel a területe? $b)$ Az elsőt úgy szeretnék keretezni, hogy a képet körülvevő szegély területe pontosan a kép területével legyen egyenlő, és a szegély mind a négy oldalon ugyanolyan széles legyen. Mekkora az így kapott, keretezendő kép kerülete? $c)$ A második kapjon olyan szegélyt keretezés előtt, hogy az oldalak aránya változzon $7:16$-ra. Ennek a szegélynek a területe $1300\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math>}$ legyen, úgy, hogy a bal és jobb oldalon egyenlő, illetve lent és fent is egyenlő szélességű. Milyen széles lesz a szegély a grafika egyes oldalai mentén?  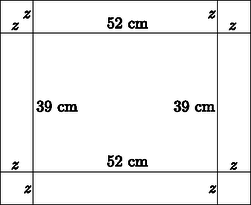(14 pont)   Megoldás. $a)$ Az első téglalap oldalainak hossza legyen $3x$ cm és $4x$ cm. Ekkor a Pitagorasz-tétel alapján: ${\left(3x\right)}^2+{\left(4x\right)}^2={65}^2$, amiből $x=13$. A téglalap oldalainak hossza: 39 cm és 52 cm, a területe: 2028 cm${}^2$. A második téglalap oldalainak hossza legyen $5y$ cm és $12y$ cm. Ekkor a Pitagorasz-tétel alapján: ${\left(5y\right)}^2+{\left(12y\right)}^2={65}^2$, amiből $y=5$. A téglalap oldalainak hossza: 25 cm és 60 cm, a területe: 1500 cm${}^2$. Vagyis az első grafika területe 528 cm${}^2$-rel nagyobb. $b)$ Már tudjuk, hogy ez a grafika 39 cm-szer 52 cm-es méretű. A szegély szélessége legyen mindenütt $z$ cm. Ekkor a szegély 2‐2 egybevágó téglalapra és 4 négyzetre bontható.     Ezek alapján felírható a következő egyenlet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\cdot 52\cdot z+2\cdot 39\cdot z+4\cdot z^2}& {\displaystyle =\mathrm{2028,}}\hfill \\ \hfill {\displaystyle 2z^2+91z-1014}& {\displaystyle =0.}\hfill \end{array}}$ Megoldóképlettel az egyenlet pozitív gyökének kétszeresére van szükségünk, hiszen a keretezendő grafika szélessége és magassága is ennyivel növekedik: $2z\approx 18\mathrm{,}5$. A megváltozott oldalhosszak: 57,5 cm és 70,5 cm. Vagyis a keretezendő kép kerülete: $2\left(57\mathrm{,}5+70\mathrm{,}5\right)=256$ cm. 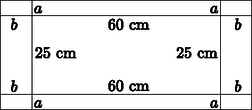$c)$ A szegélyekkel növelt kép oldalainak hossza: $25+2a$ és $60+2b$.     A következő arány ismert: $\frac{25+2a}{60+2b}=\frac{7}{16}$, $32a+400=14b+420$, $a=\frac{7b+10}{16}$. A szegély 8 téglalapra bontható, melyek közül 2-2-4 egybevágó. Ezek alapján felírható a következő egyenlet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\cdot 60a+2\cdot 25b+4\cdot ab}& {\displaystyle =\mathrm{1300,}}\hfill \\ \hfill {\displaystyle 2ab+60a+25b-650}& {\displaystyle =0.}\hfill \end{array}}$ Ebbe az egyenletbe behelyettesíthető az $a$-ra kapott kifejezés: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\cdot \frac{7b+10}{16}\cdot b+60\cdot \frac{7b+10}{16}+25b-650}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle b^2+60b-700}& {\displaystyle =0.}\hfill \end{array}}$ Megoldóképlettel az egyenlet pozitív gyöke: $b=10$. Ekkor $a=\frac{7\cdot 10+10}{16}=5$. Vagyis a grafika jobb és bal szélén 10‐10 cm, fönt és lent 5‐5 cm széles lesz a szegély.   II. rész     5. Adott a valós számok halmazán értelmezett $f\left(x\right)=x^2-42x+425$ hozzárendelésű függvény. $a)$ Igazoljuk, hogy az $f\left(x\right)$ függvény képére illeszkedő $15$, $20$, $24$ és $25$ abszcisszájú pontok húrnégyszöget határoznak meg. Adjuk meg a körülírható kör középpontját és sugarát. $b)$ Mekkora területű síkidomot határol az $f\left(x\right)$ függvény képe és az $x$ tengely? $c)$ Adjuk meg az $f\left(x\right)$ függvény grafikonját a $\left(20;-15\right)$ pontban érintő egyenes egyenletét.  (16 pont)   Megoldás. $a)$ Behelyettesítéssel megadhatók a pontok második koordinátái is: ${\displaystyle \begin{array}{cc}{\displaystyle \text{ Mivel <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>15</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mrow><msup><mrow><mn>15</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>42</mn><mo>⋅</mo><mn>15</mn><mo stretchy="false">+</mo><mn>425</mn><mo stretchy="false">=</mo><mn>20</mn></math>,}}\hfill & {\displaystyle \text{ezért <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>A</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>15</mn><mi>;</mi><mn>20</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>.}}\hfill \\ {\displaystyle \text{ Mivel <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>20</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mrow><msup><mrow><mn>20</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>42</mn><mo>⋅</mo><mn>20</mn><mo stretchy="false">+</mo><mn>425</mn><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>15</mn></math>,}}\hfill & {\displaystyle \text{ezért <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>20</mn><mi>;</mi><mo stretchy="false">-</mo><mn>15</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>.}}\hfill \\ {\displaystyle \text{ Mivel <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>24</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mrow><msup><mrow><mn>24</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>42</mn><mo>⋅</mo><mn>24</mn><mo stretchy="false">+</mo><mn>425</mn><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>7</mn></math>,}}\hfill & {\displaystyle \text{ezért <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>C</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>24</mn><mi>;</mi><mo stretchy="false">-</mo><mn>7</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>.}}\hfill \\ {\displaystyle \text{ Mivel <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>f</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>25</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow><mo stretchy="false">=</mo><mrow><msup><mrow><mn>25</mn></mrow><mrow><mn>2</mn></mrow></msup></mrow><mo stretchy="false">-</mo><mn>42</mn><mo>⋅</mo><mn>25</mn><mo stretchy="false">+</mo><mn>425</mn><mo stretchy="false">=</mo><mn>0</mn></math>,}}\hfill & {\displaystyle \text{ezért <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>D</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>25</mn><mi>;</mi><mn>0</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>. }}\hfill \end{array}}$ Ha $ABCD$ húrnégyszög lenne, akkor bármelyik két csúcsot összekötő szakasz ugyanannak a körnek a húrja lenne. A húr felezőmerőlegesére illeszkedik a kör középpontja, ezért két húr felezőmerőlegesének metszéspontja adhatja a keresett kör középpontját. Az $AD$ húr $f$ felezőmerőlegese átmegy az $AD$ szakasz $P$ felezőpontján: $P\left(20;10\right)$, és egyik normálvektora: $\overrightarrow{AD}\left(25-15;0-20\right)$, de vehetjük a hosszának a tizedét: $\left(1;-2\right)$. Ezeket felhasználva az $f$ egyenes egyenlete: $x-2y=0$. Az $BC$ húr $g$ felezőmerőlegese átmegy a $BC$ szakasz $Q$ felezőpontján: $Q\left(22;-11\right)$, és egyik normálvektora: $\overrightarrow{BC}\left(24-20;-7-\left(-15\right)\right)$, de vehetjük a hosszának a negyedét: $\left(1;2\right)$. Ezeket felhasználva a $g$ egyenes egyenlete: $x+2y=0$. Az $f$ és a $g$ egyenes az origóban metszi egymást. Mivel $OA=OD=25$ és $OB=OC=25$, ezért a négy pont az origó középpontú 25 egység sugarú körre illeszkedik, vagyis valóban húrnégyszöget alkot. $b)$ Az $f$ függvény hozzárendelési szabályát alakítsuk át: $\begin{array}{c}{\displaystyle f\left(x\right)=x^2-42x+425={\left(x-21\right)}^2-16.}\end{array}$ Ez azt jelenti, hogy a $g\left(x\right)=x^2$ hozzárendelésű függvény $\left(21;-16\right)$ vektorral történő eltolásával kapjuk $f\left(x\right)$-et. A terület meghatározásánál kényelmesebb a számolás, ha $g\left(x\right)$-hez kapcsolódóan határozzuk meg a megfelelő síkidom területét, azaz a $\left[-4;4\right]$ intervallumon a görbe alatti területet kell kivonnunk a 8-szor 16-os téglalap területéből. A görbe alatti területet határozott integrállal határozhatjuk meg: $\begin{array}{c}{\displaystyle \underset{-4}{\overset{4}{\int }}{x}^{2}dx={\left[\frac{x^3}{3}\right]}_{-4}^4=\frac{4^3}{3}-\frac{{\left(-4\right)}^3}{3}=\frac{128}{3}\mathrm{.}}\end{array}$ A keresett terület: $8\cdot 16-\frac{128}{3}=\frac{256}{3}$. $c)$ Az érintő meredekségét $f\left(x\right)$ deriváltja adja $x=20$-nál. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle f\text{'}\left(x\right)}& {\displaystyle =\left(x^2-42x+425\right)\text{'}=2x-\mathrm{42,}}\hfill \\ \hfill {\displaystyle f\text{'}\left(20\right)}& {\displaystyle =2\cdot 20-42=-2.}\hfill \end{array}}$ A $\left(20;-15\right)$ pontra illeszkedő, $-2$ meredekségű egyenes egyenlete: $y+15=-2\left(x-20\right)$, amit $2x+y=25$ alakban is írhatunk.   6. Egy kockát az oldallapjaival párhuzamos síkok mentén $n^3$ darab kisebb, egybevágó kockára vágunk. $a)$ Hány darab sík mentén történik a vágás? (A vágások alatt a részeket nem mozdítjuk el egymástól.) Egy kockát az oldallapjaival párhuzamos síkok mentén kisebb, egybevágó kockákra vágunk. $b)$ Hány darab kis kockára kell vágnunk a nagy kockát, ha ezáltal a felszín ötszöröződik? Egy fehérre festett, 9 cm élhosszúságú kockát az oldallapjaival párhuzamos síkok mentén $27$ darab egybevágó kis kockára vágtunk szét. A vágásfelületeket úgy festettük pirosra és zöldre, hogy a kis kockákból kirakható legyen egy piros, illetve egy zöld, az eredeti fehér kockával azonos méretű tömör kocka. Mekkora a valószínűsége annak, hogy az így kialakított készletből véletlenszerűen egy olyan kis kockát választhatunk, amellyel $c)$ $0\mathrm{,}5$ valószínűséggel pirosat dobunk; $d)$ csak kétféle színt dobhatunk? $e)$ A kis kockákból egy olyan lyukas kockát építünk, hogy minden lap közepén át lehet látni az építményen. Mekkora az így kapott test térfogata, felszíne?  (16 pont)   Megoldás. $a)$ Egy élt a párhuzamos síkoknak $n$ részre kell vágniuk. Ehhez $n-1$ darab sík kell. Mindhárom irányban ennyi síkra van szükség. Vagyis a síkok száma: $3n-3$. $b)$ Legyen a nagy kocka felszíne $6T$. Egy megfelelő vágás a felületet $2T$-vel növeli. Ha azt szeretnénk, hogy a felszín ötszöröződjön, akkor a felületet $24T$-vel kell növelnünk. Ezt 12 vágással érhetjük el, azaz minden irányban 4 sík mentén kell vágnunk, így $5\cdot 5\cdot 5$ darab kis kockát kapunk. Vagyis 125 kis kockának lesz a felszíne ötször annyi, mint az eredeti nagy kockáé volt. $c)$ Pontosan 8 darab kis kockán kell pontosan 3 lapot pirosra festenünk, hiszen csak ebben az esetben lehetséges a piros nagy kocka elkészítése. (A festetlen felület nagysága két nagy kocka felszínével egyenlő, ezért piros nagy kocka építése esetén minden piros felületnek, zöld nagy kocka építése esetén pedig minden zöld felületnek látszania kell.) Vagyis a keresett valószínűség: $\frac{8}{27}$. $d)$ Csak a nagy kocka középső kis kockája lehet olyan, amelyiken két szín van, hiszen egy adott színű nagy kocka összeállításánál minden adott színű lapnak a felszínen kell lennie. Vagyis a készletben 1 db 3 lapja piros, 3 lapja zöld, 1 db 3 lapja zöld, 3 lapja fehér, 1 db 3 lapja fehér, 3 lapja piros kis kockának kell lennie. Vagyis a keresett valószínűség: $\frac{3}{27}=\frac{1}{9}$. $e)$ Az építményt úgy kapjuk az eredeti nagy kockából, ha elvesszük a lapközepeken lévő kis kockát, és a középsőt. Vagyis 20 darab 3 cm élű kis kockából készíthető el. Ezért a térfogata: $V=20\cdot 3^3=540\left({\text{cm}}^3\right)$. Az összeállításnál a 8 sarok kis kockának 3 lapja van a test felületén, a 12 élfelezőnél lévő kis kockáknak pedig 4 lapja. A kis kockák lapjai 9 cm${}^2$ területűek. Ezek alapján a test felszíne: $A=9\cdot \left(8\cdot 3+12\cdot 4\right)=648\left({\text{cm}}^2\right)$.   7. $a)$ Kilenc egymást követő egész szám közül az öt kisebbnek a négyzetösszege egyenlő a négy nagyobbnak a négyzetösszegével. Adjuk meg a kilenc számot. $b)$ Igazoljuk, hogy kilenc egymást követő egész szám közül a hat kisebbnek a négyzetösszege nem lehet egyenlő a három nagyobbnak a négyzetösszegével. $c)$ Létezik-e öt olyan gömb, melyeknek sugara centiméterben mérve öt egymást követő egész szám, és a három kisebb gömb térfogatösszege egyenlő a két nagyobb gömb térfogatösszegével? $d)$ Egy téglatest két élének hossza egymást követő két egész számmal adható meg, a testátlójának hossza pedig az előző két egész szám szorzatánál $1$-gyel nagyobb. Igazoljuk, hogy a téglatest harmadik élének hossza is egész számmal adható meg.  (16 pont)   Megoldás. $a)$ Legyen a kilenc egész szám közül a középső $n$. Ekkor a következő egyenlet írható fel a szöveg alapján: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(n-4\right)}^2+{\left(n-3\right)}^2+{\left(n-2\right)}^2+{\left(n-1\right)}^2+n^2=}\hfill \\ \hfill {\displaystyle ={\left(n+1\right)}^2+{\left(n+2\right)}^2+{\left(n+3\right)}^2+{\left(n+4\right)}^2\mathrm{,}}\hfill \end{array}}$ amiből $\begin{array}{c}{\displaystyle n^2-40n=0.}\end{array}$ Az így kapott hiányos másodfokú egyenlet két gyöke: $n_1=0$, $n_2=40$. Két megoldást kaptunk: I. eset: $-4$, $-3$, $-2$, $-1$, 0, 1, 2, 3, 4. II. eset: 36, 37, 38, 39, 40, 41, 42, 43, 44. $b)$ Ebben az esetben így módosul az egyenlet: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(n-4\right)}^2+{\left(n-3\right)}^2+{\left(n-2\right)}^2+{\left(n-1\right)}^2+n^2+{\left(n+1\right)}^2=}\hfill \\ \hfill {\displaystyle ={\left(n+2\right)}^2+{\left(n+3\right)}^2+{\left(n+4\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle {3n}^2-36n+2=0.}\hfill \end{array}}$ Megoldóképlettel kapjuk, hogy $n$ nem lesz egész szám. Ezzel az állítást igazoltuk. $c)$ Legyen az öt sugár hossza centiméterben mérve $r-2$, $r-1$, $r$, $r+1$, $r+2$, ahol $r$ egy 2-nél nagyobb egész szám. A feladat szövege szerint felírhatjuk a térfogatok közötti összefüggést: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{4\pi {\left(r-2\right)}^3}{3}+\frac{4\pi {\left(r-1\right)}^3}{3}+\frac{4\pi r^3}{3}}& {\displaystyle =\frac{4\pi {\left(r+1\right)}^3}{3}+\frac{4\pi {\left(r+2\right)}^3}{3}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(r-2\right)}^3+{\left(r-1\right)}^3+r^3}& {\displaystyle ={\left(r+1\right)}^3+{\left(r+2\right)}^3\mathrm{,}}\hfill \\ \hfill {\displaystyle r^3-18r^2}& {\displaystyle =18.}\hfill \end{array}}$ Mivel $r$ egész szám, és $2$-nél nagyobb, ezért csak a $18$-nak a $2$-nél nagyobb osztói jöhetnek szóba. Ezek a számok a $3$, $6$, $9$, $18$. Behelyettesítéssel látható, hogy egyik sem jó. Vagyis nem létezik a feladat kérésének megfelelő öt gömb. $d)$ Legyen a téglatest éleinek hossza: $a$, $a+1$, $c$. Tudjuk, hogy a testátlójának hossza $a\left(a+1\right)+1=a^2+a+1$, ahol $a$ pozitív egész szám. Igazolandó, hogy a harmadik él hossza, $c$ is az. Írjuk fel a téglatest élei és testátlója közötti (a Pitagorasz-tétel kétszeri alkalmazásával kapható) kapcsolatot: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle a^2+{\left(a+1\right)}^2+c^2={\left(a^2+a+1\right)}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle c^2}& {\displaystyle ={\left(a^2+a+1\right)}^2-a^2-{\left(a+1\right)}^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =a^4+a^2+1+2a^3+2a^2+2a-a^2-a^2-2a-\mathrm{1,}}\hfill \\ \hfill {\displaystyle c^2}& {\displaystyle =a^4+2a^3+a^2=a^2{\left(a+1\right)}^2\mathrm{.}}\hfill \end{array}}$ Ebből következik, hogy $c=a\left(a+1\right)$. Mivel $a$ pozitív egész szám volt, ezért $c$ is az.   8. Tóbiás király (akit a mesében a nép csak Palacsintás királynak nevez) nagyon elszegényedett, ezért kénytelen volt január elsején a Derelye főszakács érdekeltségi köréhez tartozó banktól $8$ millió fabatka kölcsönt felvenni. A Derelye Bank $12$ évi futamidőre, évi $9\%$-os kamatra adta a kölcsönt, és ezt minden év végén egyenlő összegekkel kell visszafizetnie a királynak. Mennyi lesz az évente visszafizetendő törlesztőrészlet? Mennyi pénzt fizet vissza összesen $12$ év alatt a király?  (16 pont)   Megoldás. A rövidebb írásmód miatt jelöljük $a$-val a 8 millió fabatkát, és legyen $x$ az évenkénti törlesztőrészlet. Az első év végén a tartozás az $a$ összeg és annak a 9%-a, csökkentve a törlesztőrészlettel: $a\cdot 1\mathrm{,}09-x$. A második év végén a tartozás az $a\cdot 1\mathrm{,}09-x$ összeg és annak a 9%-a, csökkentve a törlesztőrészlettel: $\begin{array}{c}{\displaystyle \left(a\cdot 1\mathrm{,}09-x\right)\cdot 1\mathrm{,}09-x=a\cdot {1\mathrm{,}09}^2-1\mathrm{,}09x-x\mathrm{.}}\end{array}$ A harmadik év végén a tartozás: $\begin{array}{c}{\displaystyle \left(a\cdot {1\mathrm{,}09}^2-1\mathrm{,}09x-x\right)\cdot 1\mathrm{,}09-x=a\cdot {1\mathrm{,}09}^3-{1\mathrm{,}09}^{2}x-1\mathrm{,}09x-x\mathrm{.}}\end{array}$ Ezt továbbgondolva felírhatjuk a tartozást ilyen alakban a 12. év végére, de tudjuk, hogy ekkor ez a tartozás 0 kellene, hogy legyen: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a\cdot {1\mathrm{,}09}^{12}-{1\mathrm{,}09}^{11}x-{1\mathrm{,}09}^{10}x-\text{...}-1\mathrm{,}09x-x}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle a\cdot {1\mathrm{,}09}^{12}-x\left({1\mathrm{,}09}^{11}+{1\mathrm{,}09}^{10}+\text{...}+1\mathrm{,}09+1\right)}& {\displaystyle =0.}\hfill \end{array}}$ A zárójelben egy mértani sorozat első 12 tagjának összege szerepel. A sorozat első tagja 1, hányadosa 1,09, ezért az egyenletet írhatjuk a következő alakban (felhasználva a mértani sorozat első $n$ tagjának összegére vonatkozó képletet): ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a\cdot {1\mathrm{,}09}^{12}-x\cdot \frac{{1\mathrm{,}09}^{12}-1}{1\mathrm{,}09-1}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x=\frac{8000000\cdot {1\mathrm{,}09}^{12}\cdot \mathrm{0,09}}{{1\mathrm{,}09}^{12}-1}}& {\displaystyle \approx 1117205.}\hfill \end{array}}$ Vagyis minden év végén 1 117 205 fabatka a törlesztőrészlet. Ezek szerint 12 év alatt 13 406 460 fabatkát fizet vissza a király.   9. Bea nagyon szereti a természetet. Az egyik teljesítménytúra alkalmával egy vízszintes, sík tisztás egyik pontjából egy irányba nézve két hegycsúcsot pillantott meg. A közelebbi $C$ hegycsúcs $\gamma ={15}^{\circ }$, a távolabbi $D$ hegycsúcs pedig $\delta ={21}^{\circ }$ emelkedési szögben látszik. Tudjuk, hogy a két hegycsúcs távolsága légvonalban 1000 méter. Anita valamennyivel már közelebb van a $C$ csúcshoz, és ő a két hegycsúcsot egy közös $\alpha ={30}^{\circ }$ emelkedési szögben látja. $a)$ Milyen magasan vannak a csúcsok Bea és Anita nézőpontjához képest, ha a testmagasságukat azonosnak vehetjük? $b)$ Mekkora a távolság Bea és Anita között? $c)$ Egy $1:40000$ méretarányú turistatérképen bejelöljük Bea helyét. Hány centiméterre van ettől a ponttól a távolabbi hegycsúcs a térképen?  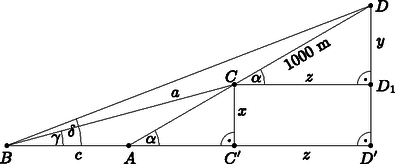(16 pont)   Megoldás. $a)$ Készítsünk a csúcsokra illeszkedő függőleges síkmetszetről egy vázlatrajzot, és használjuk az ábrán látható jelöléseket.     Mivel a $CD{D}_1$ derékszögű háromszögben $\alpha ={30}^{\circ }$, ezért $y=500$ (m). A megadott szögek alapján: $DBC\sphericalangle ={21}^{\circ }-{15}^{\circ }=6^{\circ }$, $BDC\sphericalangle ={69}^{\circ }-{60}^{\circ }=9^{\circ }$. Ezek alapján a $BCD$ háromszögben $BCD\sphericalangle ={165}^{\circ }$. Felírható a szinusztétel a $BCD$ háromszögben: $\begin{array}{c}{\displaystyle \frac{a}{1000}=\frac{\text{sin}{9}^{\circ }}{\text{sin}{6}^{\circ }}\mathrm{,}\text{vagyis}a\approx 1496\mathrm{,}6\text{(m)}\mathrm{.}}\end{array}$ A $BCC\text{'}$ derékszögű háromszögben: $\begin{array}{c}{\displaystyle x=a\cdot \text{sin}{15}^{\circ }=1496\mathrm{,}6\cdot \text{sin}{15}^{\circ }\approx 387\mathrm{,}3\text{(m)}\mathrm{.}}\end{array}$ Vagyis az alacsonyabb hegy magassága egészekre kerekítve: $x\approx 387$ m, a magasabb hegy magassága pedig: $x+y=387+500=887$ (m). $b)$ Mivel az $ACC\text{'}$ derékszögű háromszögben az $A$ csúcsnál ${30}^{\circ }$ van, ezért: $\begin{array}{c}{\displaystyle AC\text{'}=x\sqrt[]{3}=387\mathrm{,}3\cdot \sqrt[]{3}\approx 670\mathrm{,}8\text{(m). }}\end{array}$ A $BCC\text{'}$ derékszögű háromszögben: $BC\text{'}=387\mathrm{,}3\cdot \text{ctg}{15}^{\circ }\approx 1445\mathrm{,}4$ (m). Vagyis Bea és Anita távolsága: $AB=BC\text{'}-AC\text{'}=1445\mathrm{,}4-670\mathrm{,}8\approx 775$ (m). $c)$ A $BD\text{'}$ távolságot kell megadnunk a térképen: $BD\text{'}=BC\text{'}+C\text{'}D\text{'}$. A $BCC\text{'}$ derékszögű háromszögből már megkaptuk, hogy $BC\text{'}\approx 1445\mathrm{,}4$ (m). A $CD{D}_1$ derékszögű háromszögben: $z=1000\cdot \text{cos}{30}^{\circ }\approx 866\mathrm{,}0$ (m). Mivel $C\text{'}D\text{'}=z$, ezért $BD\text{'}=1445\mathrm{,}4\text{m}+866\mathrm{,}0\text{m}=2311\mathrm{,}4\text{m}=231140$ cm. Tudjuk, hogy a megadott térképen az 1 cm-es távolság a valóságban 40 000 cm. Ezért Bea és a távolabbi hegycsúcs távolsága a térképen: $\frac{231140}{40000}\approx 5\mathrm{,}8$ (cm).