Cím:	Gyakorló feladatsor emelt szintű matematika érettségire
Szerző(k):	Deák Anna
Füzet:	2017/december, 522 - 524. oldal	PDF  |  MathML
Hivatkozás(ok):	2018/január: Megoldásvázlatok a 2017/9. sz. emelt szintű matematika gyakorló feladatsorhoz

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ $A\cup B$ halmaznak 192 eleme van. $A\cap B$ elemszáma $A$ elemszámának 20%-a, $B$ elemszámának 15%-a. Hány eleme van az $A$ és a $B$ halmaznak?  (6 pont) $b)$ Egy város felnőtt lakosságának 30%-a nyugdíjas. A nyugdíjasok 55%-a nő. A férfiaknak 73%-a aktív korú (nem nyugdíjas). Bizonyítsuk be, hogy a városban a felnőtt férfiak és nők száma egyenlő.  (5 pont)   2. $a)$ Oldjuk meg az egyenletet a valós számok halmazán: $3^{2+x}+3^{6-x}=2190$.  (7 pont) $b)$ Legyen az $a_n$ sorozat definíciója: $a_n=8^{n\left(n+1\right)}$. Bizonyítsuk be, hogy a sorozat első $n$ tagjának szorzata $2^{n\left(n+1\right)\left(n+2\right)}$.  (7 pont)   3. $a)$ Egy 10 egység sugarú körbe az $ABCD$ négyszöget írtuk. A négyszög két átlója ${70}^{\circ }$-os szögben metszi egymást. Az $AC$ átló hossza $20$ egység, és a $CD$ oldallal ${40}^{\circ }$-os szöget zár be. Számítsuk ki a négyszög szögeit.  (6 pont) $b)$ Egy 10 egység sugarú gömbbe csonkakúpot írunk, melynek alap-, illetve fedőlapja a gömb középpontjától 6 cm, illetve 8 cm távolságra van. (A gömb középpontja a két sík közé esik.) Számítsuk ki a csonkakúp felszínét.  (8 pont)   4. Elemezzük monotonitás szempontjából a valós számok halmazán értelmezett $f\left(x\right)=x^4-8x^3+13\mathrm{,}5x^2+10$ függvényt, és adjuk meg lokális szélsőértékeit.  (12 pont)   II. rész 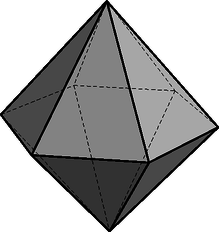    5. Egy dobókockához hasonlóan használható fajáték alakja két egybevágó, alapjuknál egymáshoz illesztett szabályos hatoldalú gúla, amelyeknek alapéle 2 cm, oldaléle 3 cm.     $a)$ Számítsuk ki a test tömegét (grammban kifejezve), ha anyagának sűrűsége 430 kg/m${}^3$.  (7 pont) $b)$ A test lapjai közül négy piros, a többi fekete. A piros dobás jelent szerencsét a társasjátékban. Ha tíz játékos dob egyszerre egy-egy ilyen testtel, mekkora a valószínűsége, hogy a játékosoknak pontosan a fele dob pirosat?  (3 pont) $c)$ A játék során a tíz játékos összesen öt alkalommal dobott egyszerre. Mindegyik alkalommal feljegyezték a piros dobások számát. Mind az öt esetben a játékosok kevesebb, mint fele dobott pirosat, de olyan nem fordult elő, hogy egyiküknek sem volt szerencséje. Mi volt az öt feljegyzett szám, ha átlaguk 1,6 és szórásuk 0,8? (A számok sorrendje nem kérdés.)  (6 pont)   6. Az ábrán látható huszonöt kör mindegyikét fehérre vagy feketére színezzük. (Az ábra rögzített, a mozgatással egymásba vihető színezéseket nem tekintjük azonosnak.)     $a)$ Hány olyan színezés lehetséges, amelyben több a fekete kör, mint a fehér?  (3 pont) $b)$ Hány olyan színezés lehetséges, amely szimmetrikus az ábra vízszintes vagy függőleges tengelyére?  (6 pont) $c)$ Hány olyan színezés lehetséges, amelyben pontosan 7 kör fekete, és szimmetrikus az ábra függőleges tengelyére?  (7 pont) 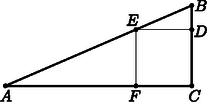  7. Az $ABC$ derékszögű háromszög befogói $AC=7$ egység, $BC=3$ egység. A háromszögbe az ábrán látható módon négyzetet írtunk.     $a)$ Milyen hosszú a négyzet oldala?  (4 pont) Az $AFE$ derékszögű háromszögbe ugyanilyen módon újabb négyzetet írunk, majd az ekkor keletkezett újabb, $A$ csúccsal rendelkező derékszögű háromszögbe újabb négyzetet stb. $b)$ Milyen hosszú a hatodik négyzet oldala?  (4 pont) $c)$ Tovább folytatva az eljárást, összesen hány négyzet oldala lesz nagyobb, mint 0,0001?  (4 pont) $d)$ Mekkora a négyzetek ,,fölött'' ($DBE$ mintájára) keletkező végtelen sok derékszögű háromszög területének összege?  (4 pont)   8. $a)$ Egy várfal nyugat-keleti irányú egyenes szakaszán négy kisméretű bástya áll, sorrendben $A$, $B$, $C$ és $D$. Az $A$ és a $D$ bástya az egyenes fal két végén helyezkedik el. Egy, az $A$ bástyától pontosan északi irányban található megfigyelőpontból az $AB$ szakasz ${31}^{\circ }$-os, a $BC$ szakasz ${17}^{\circ }$-os, a $CD$ szakasz pedig ${14}^{\circ }$-os szögben látszik. A bástyák közötti távolságok közül csak a $BC$ távolságot ismerjük, ez 200 méter. Mekkora az $AB$ és a $CD$ távolság? Készítsünk ábrát. Az eredményeket 10 m pontossággal adjuk meg.  (7 pont) $b)$ Egy egyenlőszárú háromszög szárhoz tartozó súlyvonala az alappal ${20}^{\circ }$-os szöget zár be. Mekkorák a háromszög szögei?  (9 pont)   9. Két, véletlenszám-generátor segítségével előállított 0 és 10 közötti számot jelöljünk $x$-szel és $y$-nal. Adjuk meg, mekkora az alábbi események valószínűsége: $\begin{array}{c}{\displaystyle A:x+y\le 8;B:x^2+y^2+49\le 10\left(x+y\right);C:20y\ge x^2\mathrm{.}}\end{array}$  (16 pont)