Cím:	Az Arnold-féle diszkrét macska-leképezés
Szerző(k):	Mincsovicsné Sélley Fanni
Füzet:	2017/december, 514 - 520. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Bevezetés Legyenek $x_0$ és $y_0$ a 0 és 1 közötti számok, valamint 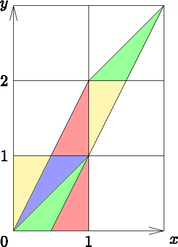${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_1}& {\displaystyle =x_0+y_0}\hfill & {\displaystyle \left(\text{mod}1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y_1}& {\displaystyle =x_0+2y_0}\hfill & {\displaystyle \left(\text{mod}1\right)\mathrm{,}}\hfill \end{array}}}& \text{(<mn>1</mn>)}\end{array}}$ ahol a mod 1 kifejezés törtrész vételét jelenti. Az 1. ábra szemlélteti, hogy mi történik az egységnégyzettel, ha minden pontjára végrehajtjuk ezt a leképezést: egy irányba megnyúlik, egy másik irányba összeszűkül, majd az így kapott parallelogrammát a mod 1 művelet visszadarabolja az egységnégyzetbe.   1. ábra. Az egységnégyzet képe az Arnold-féle macska-leképezés hatása alatt   Vlagyimir Arnold orosz matematikus után Arnold-féle macska-leképezésnek szokás ezt nevezni, mivel Arnold egy macska képével szemléltette a leképezés hatását. A leképezés érdekessége abból ered, hogy egyszerűsége ellenére erősen kaotikus. Ezalatt azt értjük, hogy ha ismételten végrehajtjuk a leképezést, az egységnégyzet pontjai gyorsan és alaposan megkeverednek. Ennek az az oka, hogy bármely pont egy irányban távolodik az eredeti ,,szomszédaitól'' (amerre nyúlik a négyzet), egy másik irányban pedig közeledik hozzájuk (amerre szűkül a négyzet). De hogyan is szimulálhatta Arnold ezt a leképezést? A következő eljárás a kézenfekvő: tekintsünk egy $N\times N$ pixel méretű képet, és alkalmazzuk az (1) leképezést minden pixelre. A pixelek koordinátáit legkényelmesebb egész számokban megadni, azaz a következő leképezést alkalmazzuk: 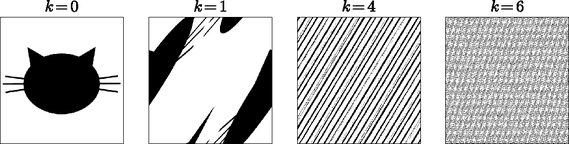${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_{k+1}}& {\displaystyle =x_k+y_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y_{k+1}}& {\displaystyle =x_k+2y_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}k=\mathrm{0,1,2,}\text{...}\mathrm{,}}\hfill \end{array}}}& \text{(<mn>2</mn>)}\end{array}}$ ahol $x_k$ és $y_k$ a $0$ és $N-1$ közötti számok. Mivel a mod $N$ kifejezés az $N$-nel való osztás maradékát veszi, $x_{k+1}$ és $y_{k+1}$ szintén $0$ és $N-1$ közé esik.   2. ábra. Macskából káoszba ($k=$ iterációk száma, $N=400$)   Kezdetben úgy tűnik, hogy a (2) leképezés teljesen összekeveri a képünk pontjait, ahogyan a folytonos változata is. Viszont némi számítógépes kísérletezés után meglepő módon azt tapasztaljuk, hogy kezdeti képünk előbb-utóbb újra megjelenik. De ha egy kicsit jobban belegondolunk, akkor láthatjuk, hogy maga a visszatérés ténye még nem igazán meglepő.   1. feladat. Tegyük fel, hogy a kép minden pixele csak fekete vagy fehér lehet. Mutassuk meg, hogy $2^{N^2}$ iteráció alatt legalább egy visszatérést tapasztalunk.   Ami viszont meglepő, hogy közel sincs szükség ilyen sok iterációra. A 3. ábrán egy olyan esetet láthatunk, ahol kevesebb, mint $N/2$ iterációra van szükség a visszatéréshez. A következőkben áttekintünk pár egyszerűbb állítást a visszatérési időről.   3. ábra. Visszatér a macska ($k=$ iterációk száma, $N=241$)     2. Visszatérési idő Visszatérési időnek fogjuk nevezni azt az iterációszámot, amelyre először visszatér az eredeti képünk. Pontosabban, a visszatérési idő az a legkisebb $m_N$ szám, amelyre ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x_{m_N}}& {\displaystyle =x_0\mathrm{,}}\hfill \\ \hfill {\displaystyle y_{m_N}}& {\displaystyle =y_0}\hfill \end{array}}$ teljesül az egységnégyzet valamennyi $\left(x_0\mathrm{,}{y}_0\right)$ pontjára. Fogalmazzuk át ezt a definíciót.   2. feladat. Lássuk be, hogy ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_k}& {\displaystyle =u_{2k-1}{x}_0+u_{2k}{y}_0}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y_k}& {\displaystyle =u_{2k}{x}_0+u_{2k+1}{y}_0}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \end{array}}}& \text{(<mn>3</mn>)}\end{array}}$ ahol $u_i$ az $i$-edik Fibonacci szám (azaz $u_0=0$, $u_1=1$, továbbá $u_{i+1}=u_i+u_{i-1}$, $i=\mathrm{0,1,}\text{...}$).   Tehát a legkisebb olyan $k$ számot keressük, amelyre ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle u_{2k-1}}& {\displaystyle \equiv 1}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle u_{2k}}& {\displaystyle \equiv 0}\hfill & {\displaystyle \left(\text{mod}N\right)}\hfill \end{array}}}\end{array}}$ teljesül (azaz $u_{2k-1}$ $N$-nel való osztás után 1 maradékot ad, $u_{2k}$ pedig nullát). Ez a két feltétel elég, hiszen ezekből $u_{2k-1}\equiv 1\left(\text{mod}N\right)$ következik. Úgy is mondhatjuk, hogy a visszatérési idő egyenlő a Fibonacci számok modulo $N$ periódusának felével. Ezt a periódust szokás Pisano-periódusnak is nevezni. Sajnos zárt formula nem ismert rá, de az idevágó ismereteink jó összefoglalását adja D. D. Wall cikke [9]. A pontos képlet hiányának ellenére léteznek eredmények, amelyek felső korlátot adnak a visszatérési időre. Ezek az állítások egyszerű számelméleti eszközökkel, ám helyenként rendkívül aprólékos munkával bizonyíthatók. Az alábbi állítást Freeman J. Dyson és Harold Falk bizonyította:   1. tétel (Dyson‐Falk [5]). Legyen $N>2$. Ekkor a visszatérési időre fennáll az $\begin{array}{c}{\displaystyle m_N\le \frac{N^2}{2}}\end{array}$ felső korlát.   Mielőtt rátérnénk a bizonyításra, megjegyezzük, hogy Freeman Dyson neves elméleti fizikus és matematikus, aki leginkább a kvantumelektrodinamika elméletének kidolgozásában vállalt szerepe miatt híres. Jelentőségét a matematikában a róla elnevezett Dyson-transzformált bizonyítja, amely az additív számelmélet egyik alapvető eszköze. Lássuk most Dyson és Falk bizonyítását, amely a N. Vorobiev könyvében [8] leírt módszert követi.   Bizonyítás. Legyen ${\Phi }_k$ az $u_k$ Fibonacci-szám $N$-nel való osztási maradéka. Tekintsük a $\begin{array}{c}{\displaystyle \langle {\Phi }_0\mathrm{,}{\Phi }_1\rangle \mathrm{,}\langle {\Phi }_1\mathrm{,}{\Phi }_2\rangle \mathrm{,}\text{...}\mathrm{,}\langle {\Phi }_k\mathrm{,}{\Phi }_{k+1}\rangle \mathrm{,}\text{...}}\end{array}$ (4) rendezett párokat. Vegyük észre, hogy $\langle {\Phi }_0\mathrm{,}{\Phi }_1\rangle =\langle \mathrm{0,1}\rangle$. Ebben a sorozatban legfeljebb $N^2$ különböző elem lehet, tehát bármely $N^2+1$ elem között szükségszerűen lesz legalább két megegyező. Most bebizonyítunk egy lemmát, hogy aztán tovább haladhassunk a tétel bizonyításával.   1. lemma. Az első ismétlődő páros a $\langle \mathrm{0,1}\rangle$.   Bizonyítás. Indirekten fogunk érvelni. Tegyük fel, hogy az első ismétlődő pár $\langle {\Phi }_k\mathrm{,}{\Phi }_{k+1}\rangle$ valamely $k>0$ számra. Tekintsünk ekkor egy olyan $\langle {\Phi }_r\mathrm{,}{\Phi }_{r+1}\rangle$, $r>k$ párost, amely megegyezik vele, azaz ${\Phi }_k={\Phi }_r$ és ${\Phi }_{k+1}={\Phi }_{r+1}$. Ekkor a Fibonacci-számok definíciója alapján ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle {\Phi }_{r-1}}& {\displaystyle \equiv {\Phi }_{r+1}-{\Phi }_r}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle {\Phi }_{k-1}}& {\displaystyle \equiv {\Phi }_{k+1}-{\Phi }_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \end{array}}}\end{array}}$ azaz ${\Phi }_{r-1}={\Phi }_{k-1}$. Tehát $\begin{array}{c}{\displaystyle \langle {\Phi }_{k-1}\mathrm{,}{\Phi }_k\rangle =\langle {\Phi }_{r-1}\mathrm{,}{\Phi }_r\rangle \mathrm{,}}\end{array}$ azaz $\langle {\Phi }_{k-1}\mathrm{,}{\Phi }_k\rangle$ is ismétlődik, és korábban van a (4) sorozatban, mint $\langle {\Phi }_k\mathrm{,}{\Phi }_{k+1}\rangle$ ‐ ellentmondásra jutottunk. Tehát $k=0$, és így $\langle {\Phi }_k\mathrm{,}{\Phi }_{k+1}\rangle =\langle {\Phi }_0\mathrm{,}{\Phi }_1\rangle =\langle \mathrm{0,1}\rangle$.  $\square$   3. feladat. Lássuk be az előző lemma segítségével a következőt: tetszőleges $N$ számra igaz, hogy az ($u_0$ utáni) első $N^2$ Fibonacci-szám között lesz legalább egy $N$-nel osztható.   2. lemma. Legyen $N>2$. Ha $u_k\equiv 0\left(\text{mod}N\right)$ és $u_{k+1}\equiv 1\left(\text{mod}N\right)$, akkor $k$ páros.   Bizonyítás. Vezessük be a  $\begin{array}{c}{\displaystyle D_k=u_k{u}_{k+2}-u_{k+1}^2}\end{array}$ mennyiséget. $D_0=-1$, valamint $D_{k+1}=-D_k$, hiszen ${\displaystyle \begin{array}{cc}\hfill {\displaystyle u_{k+1}{u}_{k+3}-u_{k+2}^2}& {\displaystyle =\left(u_{k+2}-u_k\right)\left(u_{k+1}+u_{k+2}\right)-u_{k+2}^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =u_{k+2}{u}_{k+1}-u_k{u}_{k+1}-u_k{u}_{k+2}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-u_k{u}_{k+2}+\left(u_{k+2}-u_k\right)u_{k+1}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-u_k{u}_{k+2}+u_{k+1}^2\mathrm{.}}\hfill \end{array}}$ Tehát $D_k=-1$, ha $k$ páros, és $D_k=1$, ha páratlan. Amennyiben $u_k\equiv 0\left(\text{mod}N\right)$ és $u_{k+1}\equiv 1\left(\text{mod}N\right)$, akkor $D_k\equiv -1\left(\text{mod}N\right)$ ‐ így $k$ páros.  $\square$   Innen már könnyű a tétel bizonyítása: tekintsük a ${\Phi }_0\mathrm{,}{\Phi }_1\mathrm{,}\text{...}$ sorozatot. A ${\Phi }_0\mathrm{,}{\Phi }_1\mathrm{,}\text{...}\mathrm{,}{\Phi }_{N^2+1}$ kezdőszeletben ismétlődni fog 0,1 ‐ legyen az első ismétlődés ${\Phi }_t\mathrm{,}{\Phi }_{t+1}$. A 2. lemma alapján $t$ páros, a visszatérési idő definíciója szerint pedig $2m_N=t$. Azaz $m_N\le N^2/2$.  $\square$   Egy általánosabb, de kevésbé explicit képletet ad a visszatérési időre Gregory Gaspari:   2. tétel (Gaspari [6]). Legyen $N$ prímtényezős felbontása $N=p_1^{{\alpha }_1}\text{...}{p}_k^{{\alpha }_k}$, ahol $p_j$ prím, és ${\alpha }_j\in \text{N}$ minden $j=\mathrm{1,}\text{...}\mathrm{,}k$ esetében. Ekkor $\begin{array}{c}{\displaystyle m_N=\text{LKKT}\left\{m_{p_1^{{\alpha }_1}}\mathrm{,}\text{...}\mathrm{,}{m}_{p_k^{{\alpha }_k}}\right\}\mathrm{,}}\end{array}$ ahol $\text{LKKT}$ a legkisebb közös többszöröst jelöli.   Megemlítjük, hogy a tétel Fibonacci-számok periódusára vonatkozó megfogalmazása már szerepelt D. D. Wall jóval korábbi cikkében [9]. A Gaspari által adott bizonyítás a következő.   Bizonyítás. Kezdjük a bizonyítást egy észrevétellel: azt állítjuk, hogy ha $K$ osztja $N$-et, akkor $m_K$ osztja $m_N$-et. Mivel ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle u_{2m_N-1}}& {\displaystyle \equiv 1}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle u_{2m_N}}& {\displaystyle \equiv 0}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \end{array}}}\end{array}}$ és $K$ osztja $N$-et, azért $u_{2m_N-1}-1$ a $K$-val osztva is 1 maradékot ad, valamint $u_{2m_N}$ a $K$-val is osztható. Azaz ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle u_{2m_N-1}}& {\displaystyle \equiv 1}\hfill & {\displaystyle \left(\text{mod}K\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle u_{2m_N}}& {\displaystyle \equiv 0}\hfill & {\displaystyle \left(\text{mod}K\right)\mathrm{.}}\hfill \end{array}}}& \text{(<mn>5</mn>)}\end{array}}$ Mivel $m_K$ a legkisebb szám, amire az (5) kongruencia-rendszer teljesül, $m_K$ kisebb (vagy egyenlő) mint $m_N$. Tegyük fel, hogy $m_N$ az $m_K$-val osztva nemnulla maradékot ad, azaz $m_N=q{m}_K+r$, ahol $0<r<m_K$, és $q$ egész. Ekkor $q{m}_K$ iteráció alatt visszatér a képünk $q$-szor, és mivel $m_N$ iteráció alatt visszatér, $r$ iteráció alatt is vissza kell térnie. De $r<m_K$, és $m_K$ volt a legkisebb idő, ami alatt visszatér a kép, tehát ellentmondásra jutottunk. Azaz $r=0$, és ezzel beláttuk az észrevételt. Térjünk rá a tétel bizonyítására. Tetszőleges $j\in \left\{\mathrm{1,}\text{...}\mathrm{,}k\right\}$ esetében $p_j^{{\alpha }_j}$ osztja $N$-et, tehát az előző észrevételünk miatt $m_{p_j^{{\alpha }_j}}$ osztja $m_N$-et. Ebből következik, hogy $m_N$ közös többszöröse az $m_{p_j^{{\alpha }_j}}$, $j\in \left\{\mathrm{1,}\text{...}\mathrm{,}k\right\}$ számoknak. Legyen $M$ egy közös többszöröse a $m_{p_j^{{\alpha }_j}}$, $j\in \left\{\mathrm{1,}\text{...}\mathrm{,}k\right\}$ számoknak. Ekkor ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle u_{2M-1}}& {\displaystyle \equiv 1}\hfill & {\displaystyle {\left(\text{mod}p\right)}_j^{{\alpha }_j}\mathrm{,}}\hfill \\ \hfill {\displaystyle u_{2M}}& {\displaystyle \equiv 0}\hfill & {\displaystyle {\left(\text{mod}p\right)}_j^{{\alpha }_j}\mathrm{.}}\hfill \end{array}}}\end{array}}$ Mivel a $p_j^{{\alpha }_j}$ számok különböző prímek hatványaiként páronként relatív prímek, ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle u_{2M-1}}& {\displaystyle \equiv 1}\hfill & {\displaystyle {\left(\text{mod}p\right)}_1^{{\alpha }_1}\text{...}{p}_k^{{\alpha }_k}=N\mathrm{,}}\hfill \\ \hfill {\displaystyle u_{2M}}& {\displaystyle \equiv 0}\hfill & {\displaystyle {\left(\text{mod}p\right)}_1^{{\alpha }_1}\text{...}{p}_k^{{\alpha }_k}=N\mathrm{.}}\hfill \end{array}}}\end{array}}$ Viszont ez azt jelenti, hogy $m_N$ osztja $M$-et. Mivel $m_N$ a legkisebb egész szám, amire a fenti kongruencia teljesül, $m_N$ a legkisebb közös többszöröse az $m_{p_j^{{\alpha }_j}}$ számoknak.  $\square$   Tehát elég prímhatványokra tudni a visszatérési időt, ebből már tetszőleges számra kiszámítható. De ez még így sem egyszerű feladat. Gaspari cikkének a függelékében $m=\mathrm{1,}\text{...}\mathrm{,195}$ periódusokra kigyűjtötte az összes $p$ prímet, amelyre $m_p=m$ ‐ ez nyújthat némi segítséget.   4. feladat. Lá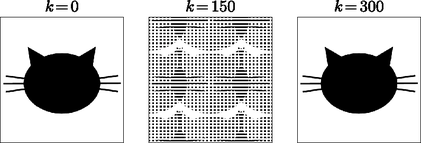ssuk be, hogy $a)$ $m_{241}=120$ (3. ábra), $b)$ $m_{400}=300$ (4. ábra).   4. ábra. $N=400$, $m_N=300$     4*. feladat. Tegyük fel, hogy $m_N$ páros. Milyen $N$-ek esetében fordul elő hogy $m_N/2$ iteráció után fejtetőn jelenik meg a macska, ahogyan a 3. ábrán is látható? A 4. ábra mutatja, hogy nem mindig ez a helyzet. Itt úgynevezett szellemképek jelennek meg, a magyarázatért lásd a [3] hivatkozást.   3. Alkalmazások Bár első ránézésre Arnold macska-leképezése csak egy matematikai játéknak tűnik, a kaotikusságát kihasználva praktikus alkalmazásai is lehetnek. A következő gyűjtés a [7] hivatkozásra támaszkodik. A legnyilvánvalóbb egy kép vagy szöveg titkosítása: a kép pixeleire, vagy a szöveg $N\times N$-es blokkba rendezett karaktereire alkalmazzuk a macska-leképezés egy megfelelő hatványát. Így alaposan megkeverednek a képpontok (vagy a betűk), avatatlan szemlélő nem képes az eredeti üzenetet visszafejteni. Tovább bonyolítható a helyzet, ha a titkosító egy általánosabb macska-leképezést használ, például az ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_{k+1}}& {\displaystyle =x_k+a{y}_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y_{k+1}}& {\displaystyle =a{x}_k+\left(a^2+1\right)y_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}k=\mathrm{0,1,2,}\text{...}}\hfill \end{array}}}& \text{(<mn>6</mn>)}\end{array}}$ vagy az ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\displaystyle \begin{array}{ccc}\hfill {\displaystyle x_{k+1}}& {\displaystyle =x_k+a{y}_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle y_{k+1}}& {\displaystyle =b{x}_k+\left(ab+1\right)y_k}\hfill & {\displaystyle \left(\text{mod}N\right)\mathrm{,}k=\mathrm{0,1,2,}\text{...}}\hfill \end{array}}}& \text{(<mn>7</mn>)}\end{array}}$ iterációt. Így az eredeti üzenet csakis az $a\mathrm{,}b$ egész számok ismeretében fejthető vissza. Ezeknek a macska-leképezéseknek a viselkedése teljesen hasonló Arnold macskájához. A visszatérési időkről J. Bao és Q. Yang ír a [2] cikkben. Egy kicsit izgalmasabb alkalmazás a szteganográfiához köthető. A szteganográfia olyan titkos üzenetek létrehozásának tudománya, amelyek létezéséről a feladón kívül csak a címzett tud ‐ szemben a kriptográfiával, ahol az üzenet léte nem rejtély, csak a tartalma. A két módszer együttes alkalmazása természetesen a leghatékonyabb. Tegyük fel, hogy van egy képünk, amiről később majd meg akarjuk állapítani, hogy valaki manipulálta-e. A következő a módszerünk: alkalmazzuk a képünkre a macska-leképezés $k$ darab iterációját, majd helyezzünk rá egy kis vízjelet. Ezután $m_N-k$ iterációval állítsuk vissza az eredeti képet, amelyen a vízjel egy hétköznapi szemlélőnek láthatatlan, hiszen a pixelei alaposan szétszóródtak. Ha később meg akarjuk állapítani, hogy valaki módosította-e a képet, elég a macska-leképezés $k$ iterációját alkalmazni rá: ha a kép nem lett manipulálva, akkor bár a kép káoszba fullad, a vízjel eredeti állapotában megjelenik a sarokban. A részletek a [4] cikkben találhatók.   Hivatkozások [1] V.I. Arnold and A. Avez, Ergodic problems of classical mechanics, W.A. Benjamin, New York (1968). [2] Jianghong Bao and Qigui Yang, Period of the discrete arnold cat map and general cat map, Nonlinear Dynamics, 70(2) (2012), 1365‐1375. [3] Ehrhard Behrends, The ghosts of the cat, Ergodic Theory and Dynamical Systems, 18(2) (1998), 321‐330. [4] Young-Long Chen, Her-Terng Yau, and Guo-Jheng Yang, A maximum entropy-based chaotic time-variant fragile watermarking scheme for image tampering detection, Entropy, 15(8) (2013), 3170‐3185. [5] Freeman J. Dyson and Harold Falk, Period of a discrete cat mapping, The American Mathematical Monthly, 99(7) (1992), 603‐614. [6] Gregory Gaspari, The Arnold cat map on prime lattices, Physica D: Nonlinear Phenomena, 73(4) (1994), 352‐372. [7] Fredrik Svanström, Properties of a generalized Arnold's discrete cat map (2014). [8] Nicolai N. Vorobiev, Fibonacci numbers, Birkhäuser (2012). [9] D.D. Wall, Fibonacci series modulo $m$, The American Mathematical Monthly, 67(6) (1960), 525‐532.