|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész
1. Oldjuk meg a valós számok halmazán az alábbi egyenlőtlenséget, illetve egyenletet:
; (5 pont)
. (6 pont)
Megoldás. Az egyenlőtlenségnek csak akkor van értelme, ha , azaz vagy . A 4-es alapú logaritmusfüggvény szigorúan monoton növekedő, ezért , melyet rendezve .
Az egyenlet gyökei és 4. Mivel az egyenlőtlenségben a másodfokú tag együtthatója pozitív, ezért .
A kapott gyököket az értelmezési tartománnyal összevetve az eredeti egyenlőtlenség megoldáshalmaza
I. megoldás (esetszétválasztással). Ha , akkor , melynek gyökei és 1. A kapott gyököket a feltétellel összevetve csak az 1 jó.
Ha , akkor , melynek nincs megoldása a valós számok halmazán.
Ha , akkor , .
Ellenőrzés behelyettesítéssel vagy az ekvivalens átalakításokra történő hivatkozás.
II. megoldás (értékkészlet vizsgálattal). Az egyenlet bal oldalán álló kifejezés nemnegatív, ezért a jobb oldalon álló kifejezésnek is nemnegatívnak kell lennie. Mivel , ezért az abszolútérték-jel elhagyható.
Ha , akkor , melynek gyökei és 1. A kapott gyököket a feltétellel összevetve csak az 1 jó.
Ha , akkor , .
Ellenőrzés behelyettesítéssel vagy az ekvivalens átalakításokra történő hivatkozás.
2. Egy ismert hazai társasjáték játéktábláján körben egymás után sorszámozott mező található. A játékosok az . sorszámú START mezőről indulnak, és mindig annyit lépnek előre, amennyit egy szabályos dobókockával dobnak. Ha egy játékos bábujával olyan mezőre lép, ahol már áll egy másik bábu, akkor kiüti azt, és a kiütött bábut a START mezőre visszahelyezi. A játékosok a játékot játékpénzzel játsszák, és annak megkezdésekor mindenki 20 000 Ft kezdőösszeggel indul.
Hányféle sorrendben számolhat le a pénztáros Csabának 2 db 5000 Ft-os, 8 db 1000 Ft-os, 3 db 500 Ft-os és 5 db 100 Ft-os játékpénzt? (3 pont)
Hányféle különböző címletezésben kaphatja meg Csaba a kezdőösszeget, ha csak a három nagy címlet (5000 Ft, 1000 Ft és 500 Ft) mindegyikéből kap? (4 pont)
Csaba első tizenöt dobásának átlaga 4,2 volt, és közben egyszer sem ütötték ki. Hányas sorszámú mezőn áll most Csaba figurája? (3 pont)
László figurája kettő mezővel áll Csabáé mögött, miután Csaba lépett. Mekkora annak a valószínűsége, hogy László a következő dobásával kiüti Csabát? (2 pont)
Megoldás. A sorrendek száma: | |
A lehetséges 27 különböző címletezés a következő táblázatban látható:
Ha az első tizenöt dobás átlaga 4,2, akkor az első tizenöt dobás összege 63. Ha Csaba az 1. sorszámú mezőről indul és egyszer sem ütötték ki, akkor 40 lépés után újra az 1. sorszámú mezőn áll, tehát 63 lépés után a 24. sorszámú mezőn áll a figurája.
Egy szabályos dobókockával dobva 6-féle lehetőségünk van a dobásra (összes eset). László egyféleképpen, egy db 2-es dobással tudja kiütni Csabát (kedvező eset). A keresett valószínűség .
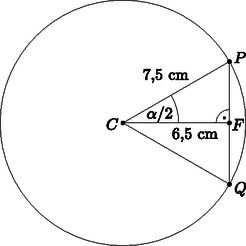
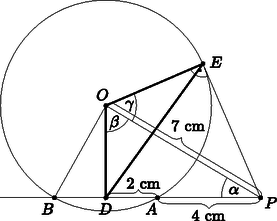
3. Egy körhöz az középpontjától 7 cm-re levő külső pontból szelőt húzunk. A szelő körrel vett és metszéspontjai -től rendre 4 cm, illetve 8 cm távolságra vannak.
Milyen hosszú érintőszakasz húzható -ből a körhöz? (3 pont)
Mekkora szögben látszik az szakasz a pontból? (4 pont)
Számítsuk ki az háromszög területét, ahol az húr felezőpontja, pedig az érintési pont. (7 pont)
Megoldás. A körhöz húzott érintő- és szelőszakaszok tétele alapján a érintőszakasz hossza: , ahonnan cm (1. ábra).
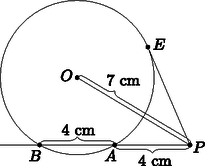 1. ábra
I. megoldás. Az szakaszt behúzva, az háromszög egyenlő szárú lesz, melynek alaphoz tartozó magassága felezi az szakaszt (2. ábra). A derékszögű háromszögben , ahonnan .
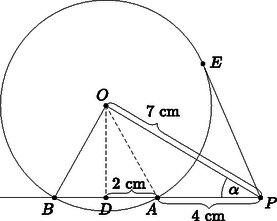 2. ábra
Az szakasz a pontból körülbelül -os szögben látszik.
II. megoldás. Mivel a érintő merőleges az érintési pontba húzott sugárra, ezért az derékszögű háromszögből Pitagorasz tételének segítségével (3. ábra). A háromszögre alkalmazva a koszinusztételt: | |
ahonnan .
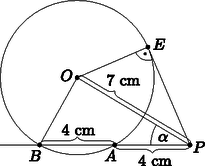 3. ábra
Az szakasz a pontból körülbelül -os szögben látszik.
A derékszögű háromszögben , ahonnan , valamint a Pitagorasz-tétel miatt (4. ábra). Az derékszögű háromszögből szintén Pitagorasz tétele miatt
 4. ábra
Az derékszögű háromszögben , ahonnan .
Az háromszög területe a trigonometrikus területképlet alapján: | |
4. Egy számtani sorozat első tagja , differenciája , egy számtani sorozat első tagja , differenciája .
Határozzuk meg, hogy hány darab háromjegyű köbszám szerepel az sorozat első tagja között. (4 pont)
A sorozat első tagja közül hányféleképpen lehet különböző számot kiválasztani úgy, hogy a kiválasztott számok mértani sorozatot alkossanak? (10 pont)
Megoldás. Az számtani sorozat 100. tagja . A 100. tagig 3 db háromjegyű köbszám van: 125, 216 és 343, melyek közül csak a 343 tagja a sorozatnak.
Olyan növekvő öttagú mértani sorozatot keresünk, amelyben minden tag a intervallumba eső pozitív egész szám.
A mértani sorozat ismert képletét alkalmazva , ahol vagy 5. Mivel a kihúzott számok különbözőek, ezért .
Az egész szám, ezért racionális szám, mely felírható pozitív egészek hányadosaként, alakban, ahol és relatív prímek.
Ha nem egész, akkor , , és ha az egész, akkor osztója -nek. Ekkor Az egyetlen ilyen lehetséges eset, ha , ; ekkor , , így a keresett számok: 16, 24, 36, 54, 81.
Ha egész, akkor lehetséges értékei 2 vagy 3, hiszen .
Ha , akkor lehetséges értékeit is figyelembe véve, a következő 4 sorozat adódik: 2, 4, 8, 16, 32; 3, 6, 12, 24, 48; 4, 8, 16, 32, 64; 5, 10, 20, 40, 80.
Ha , akkor nincs a feltételeknek megfelelő sorozat.
Tehát összesen 5 különböző kiválasztás lehetséges.
II. rész
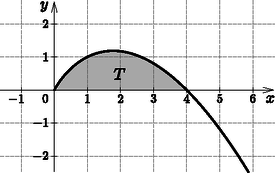
5. Adott a nemnegatív valós számok halmazán értelmezett függvény.
Adjuk meg az alábbi állítás logikai értékét (igaz vagy hamis): (8 pont)
b) Számítsuk ki az f függvény grafikonja és az x tengely által határolt korlátos síkidom területét. (8 pont)
Megoldás. a) A két pontra illeszkedő egyenes egyenletébe behelyettesítve: (x+1)⋅(0-5)=(y-5)⋅(4+1), melyből az egyenes egyenlete y=-x+4. A B-ben húzott érintő meredekségét az f deriváltfüggvényének az x=4 helyen felvett helyettesítési értéke adja meg: | f'(x)=2-32⋅x12,ahonnanf'(4)=2-32⋅4=-1. |
Az érintő egyenlete: y-0=(-1)⋅(x-4), vagyis y=-x+4.
Tehát az állítás igaz.
b) Az f függvény és az x tengely metszéspontjait a 2x-xx=0 egyenlet gyökei adják. Az egyenletet szorzattá alakítva: x(2-x)=0, melynek gyökei 0 és 4.
Mivel a (0;4) intervallumon ezért itt az f függvény grafikonja az x tengely felett helyezkedik el. Tehát a keresett T terület: | T=∫04(2x-xx)dx=[x2-25⋅x52]04=(42-25⋅452)-0=3,2. |
6. Az alábbi táblázatban egy nagyáruházban dolgozók havi bruttó bérének gyakorisága látható.
Bruttó bér (ezer Ft) 95 110 120 125 160 200 230 Gyakoriság 7 4 2 5 3 2 1
a) Melyik az a bérérték, amelynél a dolgozók legalább fele nem keres kevesebbet, legalább fele pedig nem keres többet? (2 pont)
b) Mennyivel változik a havi bruttó bérek szórása, ha a dolgozók egységesen 10%-os béremelést kapnak? (4 pont)
Az áruházban számos furfangos trükköt alkalmaznak a termékek elhelyezésére azért, hogy a vásárlók pontosan azokat az árucikkeket vegyék meg, amelyeken a bolt a legtöbbet keresi. Az egyik ilyen trükk a polcok különböző zónákra osztása, melyet az alábbi táblázatban láthatunk.
ZónákVásárlási valószínűségA polcon találhatóaz adott polcróltermékek átlagára Nyújtózkodási zóna 0,1 1400 Ft Szemmagassági zóna 0,5 900 Ft Kézzel elérhető zóna 0,3 700 Ft Lehajló zóna 0,1 400 Ft
c) Mekkora a vásárlási összeg várható értéke egy áru fenti polcrendszerről történő vásárlása esetén? (2 pont)
A nagyáruházban az egyik délután megfigyelték, hogy 65% annak a valószínűsége, hogy egy véletlenszerűen választott vásárló nő. Ebben az időszakban a nőknél 70% az esélye, hogy kártyával fizetnek, míg a férfiak csak 40%-ban fizetnek kártyával.
d) Mekkora annak a valószínűsége, hogy a pénztárnál sorban álló 8 ember közül pontosan 5 nő? (3 pont)
e) Mekkora annak a valószínűsége, hogy egy véletlenszerűen választott vásárló kártyával fizet? (5 pont)
Megoldás. a) A keresett bérérték a medián, ami 120 000 Ft.
b) Ha minden dolgozó bérét 10%-kal megemelik, akkor az átlagkereset is 10%-kal nő, mert | x¯'=1,1⋅x1+1,1⋅x2+...+1,1⋅xnn=1,1⋅(x1+x2+...+xn)n=1,1⋅x¯. |
Az előbbiek miatt a bérek szórása is 10%-kal nő, hiszen
σ'=1n⋅∑i=1n(1,1⋅xi-1,1⋅x¯)2=1n⋅∑i=1n1,12⋅(xi-x¯)2==1n⋅1,12⋅∑i=1n(xi-x¯)2=1,1⋅1n⋅∑i=1n(xi-x¯)2.
c) A vásárlási összeg várható értéke az egyes polcokon levő termékek árának és az onnan történő vásárlási valószínűségek szorzatainak összege: | E(x)=1400⋅0,1+900⋅0,5+700⋅0,3+400⋅0,1=840Ft. |
d) Annak a valószínűsége, hogy egy véletlenszerűen választott vásárló nő p=0,65, annak a valószínűsége, hogy férfi q=0,35. A binomiális eloszlás alapján a keresett valószínűség:
e) I. megoldás (feltételes valószínűség nélkül). Tekintsünk 200 főt, akik a vizsgált időszakban az áruházban vásároltak. Ekkor a vásárlók közül 130 fő nő, 70 fő pedig férfi. A nők közül 91 fő vásárolt kártyával, míg a férfiak közül 28 fő. A kártyával vásárlók száma az összes vásárló számának 119200=0,595-ed része.
A kiszámított arány független a konkrét darabszámtól, az csupán az eloszlástól függ, így a keresett valószínűség 0,595.
II. megoldás (feltételes valószínűséggel). Jelölje A azt az eseményt, hogy a kiválasztott vásárló nő, B azt, hogy a kiválasztott vásárló férfi, K pedig azt, hogy a kiválasztott vásárló kártyával fizet.
A feladat szövege alapján P(A)=0,65, P(B)=0,35, P(K∣A)=0,7, illetve P(K∣B)=0,4.
A feltételes valószínűség definíciója alapján: | P(K∣A)=P(KA)P(A),valamintP(K∣B)=P(KB)P(B). |
Annak a valószínűsége, hogy egy véletlenszerűen választott vásárló kártyával fizet: | P(K∣A)⋅P(A)+P(K∣B)⋅P(B)=0,7⋅0,65+0,4⋅0,35=0,595. |
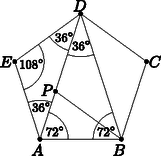
7. Adott az ábrán látható szabályos ötszög.
a) Igazoljuk, hogy az ötszögben AB2=AP⋅AD, ha P az AD átló és az ABD háromszög B csúcsából induló belső szögfelezőjének metszéspontja. (8 pont)
b) Hány különböző kört határoznak meg egy 5 pontú teljes gráf élei? (8 pont)
(Két kört azonosnak tekintünk, ha mindkettőben ugyanazok a csúcsok és ugyanazok az élek szerepelnek.)
Megoldás. a) A szabályos ötszög belső szögei 108∘-osak, ezért az ABD egyenlő szárú háromszög alapon fekvő szögei 72∘-osak, szárszöge pedig 36∘-os.
Az ABD háromszög B csúcsából induló belső szögfelezőjét behúzva, a megfelelő szögek egyenlősége miatt az ABP és BDP háromszögek is egyenlő szárúak lesznek, amiből következik, hogy AB=BP=PD.
A szögfelezőtétel szerint: APPD=ABBD, valamint PD=AB és BD=AD, amit behelyettesítve kapjuk, hogy: | APAB=ABAD,ahonnanAB2=AP⋅AD. |
Megjegyzés: A bizonyítandó állítás geometriai jelentése, hogy a P pont éppen az aranymetszés arányában osztja két részre az AD átlót.
b) Számoljuk össze a köröket a bennük szereplő élek száma alapján.
1 és 2 hosszú kör nyilván nincs a gráfban, ezek lennének ugyanis a hurokélek és a többszörös élek.
A 3 hosszú körök száma (53)=10, hiszen bármely három pont pontosan egy kört határoz meg.
A 4 hosszú körök száma (54)⋅3=15, hiszen 4 pontot (54)-féleképpen választhatunk ki, és pl. az A‐B‐C‐D; B‐C‐D‐A; C‐D‐A‐B; D‐A‐B‐C; D‐C‐B‐A stb. körök megegyeznek, de különböznek az A‐B‐D‐C és az A‐C‐B‐D és az azokkal megegyező köröktől, vagyis 4 ponthoz 3 különböző kört rendelhetünk hozzá.
5 csúcsot 5!-féleképpen rendezhetünk sorba. A ciklikus szimmetria miatt egy-egy kört 5 sorrend is meghatároz, illetve minden kör két irányba is bejárható: pl. az A‐B‐C‐D‐E kör és az A‐E‐D‐C‐B kör is megegyezik. Tehát az 5 hosszú körök száma 5!5⋅2=12.
Tehát a kérdéses körök száma 37.
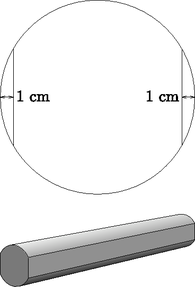
8. Egy erdei turistautat átszelő patak fölött az erdészet hidat készít, amihez 22 db 15 cm átmérőjű, henger alakú farönköt használnak, melyek hossza 1,2 m. A jobb illesztés érdekében a rönköket a forgástengelyükkel párhuzamosan, 1-1 cm-es maximális mélységben, teljes hosszukban az ábra szerint mindkét oldalon legyalulják, és ezeknek az egyenes felületeknek a mentén fogatják össze a darabokat. A híd két végénél lévő két farönköt csak az egyik oldaluknál gyalulják le.
a) Mennyi faanyagot tartalmaz a híd elkészített állapotában? (8 pont)
A farönkök legyalulása után azok mindegyikének teljes felületét egyesével lefestik.
b) Mekkora lesz az összes lefestett felület nagysága? (8 pont)
Megoldás. a) Számítsuk ki a 22 farönk térfogatát, majd vonjuk ki belőle a gyalulás során keletkező hulladék térfogatát.
A CFP derékszögű háromszögben cosα2=6,57,5, amiből α≈59,85∘. Mivel egy körben a középponti szög nagysága egyenesen arányos a hozzátartozó körcikk területével, ezért | Tkörcikk=α⋅7,52⋅π360∘(≈29,38cm2), |
valamint | TCPQ▵=7,52⋅sinα2(≈24,32cm2), |
így egy körszelet területe: | Tkörszelet=Tkörcikk-TCPQ▵≈5,06cm2. |
A keresett térfogat: | V=22⋅7,52⋅π⋅120-21⋅2⋅Tkörszelet⋅120≈0,44m3. |
A híd kb. 0,44 m3 faanyagot tartalmaz elkészített állapotában.
b) A lefestett felület nagyságának meghatározásához számítsuk ki a 22 farönk (20 db ,,középső'' és 2 db ,,szélső'') felszínét. A CFP derékszögű háromszögben egyrészt PF=PC2-FC2≈3,74cm, amiből PQ≈7,48cm; másrészt cosα2=6,57,5, amiből α≈59,85∘.
Mivel egy körben az adott középponti szöghöz tartozó ív hossza egyenesen arányos a kör kerületével, ezért
iα=α⋅2⋅7,5⋅π360∘(≈7,83cm),Tkörcikk=iα⋅7,52(≈29,38cm2),TCPQ▵=7,52⋅sinα2(≈24,32cm2),
így Tkörszelet=Tkörcikk-TCPQ▵≈5,06cm2.
Egy ,,középső'' farönk felszíne:
Talap (középső)=2⋅(7,52⋅π-2⋅Tkörszelet)(≈333,19cm2),Tpalást (középső)=(2⋅7,5⋅π-2⋅iα+2⋅PQ)⋅120(≈5570,87cm2),Aközépső=Talap (középső)+Tpalást (középső)(≈5904,06cm2).
Egy ,,szélső'' farönk felszíne:
Talap (szélső)=2⋅(7,52⋅π-Tkörszelet)(≈343,31cm2),Tpalást (szélső)=(2⋅7,5⋅π-iα+PQ)⋅120(≈5612,87cm2),Aszélső=Talap (szélső)+Tpalást (szélső)(≈5956cm2).
A lefestendő összes felület nagysága: | A=20⋅Aközépső+2⋅Aszélső≈13m2. |
A lefestett felület nagysága kb. 13 m2.
9. Tekintsük az sorozatot, ahol n∈N+.
a) Igazoljuk, hogy az {an} sorozat első n tagjának összege Sn=1-n+1n+1. (9 pont)
b) Határozzuk meg a limn→∞(1-n+1n+1) határértéket, majd adjuk meg, hogy a sorozat tagjai hányadik tagtól kezdve esnek a határérték ε=0,01 sugarú környezetébe. (7 pont)
Megoldás. a) I. megoldás (teljes indukcióval).
1. lépés: nézzük meg, hogy az állítás n=1-re igaz-e: | a1=12+2=12+2⋅2-22-2=2-22=1-22=S1, |
tehát az állítás n=1-re igaz.
2. lépés: Tegyük fel, hogy az állítás n=k-ra igaz, azaz az első k tag összege Sk=1-k+1k+1. Ez lesz az indukciós feltevés.
3. lépés: Nézzük meg, hogy n=k-ról n=(k+1)-re ,,öröklődik''-e az állítás. Bizonyítandó, hogy:
(121+12+132+23+...+1(k+1)k+kk+1)++1(k+2)k+1+(k+1)k+2=1-k+2k+2.
A zárójelben szereplő összeg az indukciós feltevés miatt Sk=1-k+1k+1, ekkor
1-k+1k+1+1(k+2)k+1+(k+1)k+2==1-k+1k+1+(k+2)k+1-(k+1)k+2(k+2)2(k+1)-(k+1)2(k+2)==1-k+1k+1+(k+2)k+1-(k+1)k+2(k+1)(k+2)==1+(k+2)k+1-(k+1)k+2-(k+2)k+1(k+1)(k+2)==1-(k+1)k+2(k+1)(k+2)=1-k+2k+2.
Ezt szerettük volna belátni.
II. megoldás. Tekintsük az {an} sorozat tetszőleges tagját: A tört nevezőjét gyöktelenítve:
1(k+1)k+kk+1⋅(k+1)k-kk+1(k+1)k-kk+1==(k+1)k-kk+1(k+1)2k-k2(k+1)=(k+1)k-kk+1k(k+1)=kk-k+1k+1.
Az előbbiek ismeretében a sorozat első n tagjának összege a következőképpen írható: | Sn=11-22+22-33+...+nn-n+1n+1. |
A teleszkópikus összeg közbülső tagjai ,,kiesnek'', így Sn=1-n+1n+1. Ezt szerettük volna belátni.
b) A tört számlálójában és nevezőjében minden tagot n-nel elosztva kapjuk, hogy: | limn→∞(1-n+1n+1)=limn→∞(1-1n+1n21+1n)=1-01=1. |
A határérték definíciója alapján: | |1-n+1n+1-1|<1100,vagyis|n+1n+1|<1100. |
Mivel n pozitív egész, ezért n+1n+1<1100, melyet rendezve 0<n2-9998n-9999. Az egyenlőtlenség pozitív zérushelye 9999, így az ennél nagyobb természetes számok megfelelnek küszöbértéknek. |
|
 PDF | MathML
PDF | MathML