Cím: Bizonyítsunk sokféleképpen! ‐ Egy érettségi feladat továbbgondolása
Szerző(k):  A matematika tételkészítő bizottság 
Füzet: 2017/november, 453 - 458. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 2017. májusi emelt szintű érettségi feladatsor egyik feladata a következő volt:

 
8. b) Az egységnyi oldalú ABC szabályos háromszög minden csúcsánál behúztunk egy-egy szögharmadoló egyenest, így az 1. ábrán látható PQR szabályos háromszöget kaptuk.


 

1. ábra
 

Számítsa ki a PQR háromszög oldalának hosszát!
 
A hivatalos javítási-értékelési útmutató három különböző megoldást közölt a feladatra, ezek megtekinthetők pl. a címen.
 
M1. Az első megoldás az ABQ háromszögben felírt két szinusztétel segítségével határozza meg a PQ oldal hosszát (2. ábra).


 

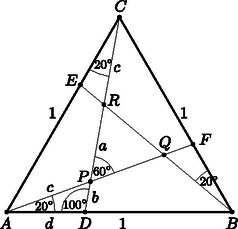2. ábra
 

 
M2. A második megoldásban egy szinusztétel és területszámítás segítségével érünk célt. TABC-TABQ=TPQR; és a szabályos háromszög területéből az oldalának hossza már számítható.
 
M3. A harmadik megoldásban szinusztételek többszöri alkalmazásával meghatározzuk a CD, majd a d, c és b szakaszhosszakat, ebből a szabályos háromszög a oldalhossza már számítható.
 
A javítási útmutatóban a megoldások végén a következő megjegyzés szerepel: ,,Addíciós tételek felhasználásával bizonyítható, hogy a=d=2⋅sin10∘.''
Jelen cikkben egyrészt elvégezzük ezt az addíciós tételek segítségével történő bizonyítást, másrészt további elemi geometriai bizonyításokat mutatunk a szabályos háromszög oldalát meghatározó a=d egyenlőségre.
 

Megjegyzés. Az a=d=2⋅sin10∘ egyenlőség igazolása addíciós tételek segítségével.
A bizonyításban felhasználjuk M3. részeredményeit:
d=sin20∘sin100∘ésa=sin60∘sin100∘-sin20∘sin60∘-sin220∘sin60∘sin100∘;
valamint alkalmazzuk a sin100∘=sin80∘ helyettesítést:
d=sin20∘sin80∘=2sin10∘cos10∘cos10∘=2sin10∘.a=sin260∘-sin220∘-sin20∘sin80∘sin60∘sin80∘==(sin60∘+sin20∘)(sin60∘-sin20∘)-sin20∘sin80∘sin60∘sin80∘==2sin40∘cos20∘⋅2sin20∘cos40∘-sin20∘sin80∘sin60∘sin80∘==sin80∘sin40∘-sin20∘sin80∘sin60∘sin80∘=sin40∘-sin20∘sin60∘=2sin10∘cos30∘sin60∘==2sin10∘.
Ezzel igazoltuk az a=d=2⋅sin10∘ egyenlőséget.

 
M4. A CER és CDA háromszögek hasonlóak (szögeik 20∘, 60∘, 100∘), így bc=d1, azaz b=cd. A CD egyenes a C középpontú egység sugarú kört M-ben metszi, AC=CM=1. AMD∢=80∘, így az MAD háromszög egyenlő szárú, és AM=d. Az MAD és ACM háromszögek hasonlóak (szögeik megegyeznek, 3. ábra), ebből MDd=d1, azaz MD=d2. Az AP egyenes szögfelezője MAC∢-nek, így az MAC háromszögben felírható a szögfelező-tétel:
d2+ba+c=d1.
Innen d2+b=da+dc, amiből a fent kapott b=cd miatt d2=da, azaz d=a következik.


 

3. ábra
 

 
Megjegyzés. A b=cd összefüggés az AMP háromszögben felírt szögfelező-tételből is megkapható, ha felhasználjuk az MAD és ACM háromszögek hasonlóságát:
DPPA=bc=DMMA=MAAC=d1.


 
A következő bizonyítás előtt segédlépésként vegyük fel az egység sugarú körbe írt szabályos 18-szög oldalait. Az előző megoldás alapján AM=MN=NB=d (4. ábra). A szabályos sokszög szimmetriatulajdonságából következik, hogy AB átlója és MN oldala párhuzamos.


 

4. ábra
 

 
M5. Felmérjük PA-ra A-n túl AL=d-t, és azt fogjuk igazolni, hogy PL=PC.
LAM egyenlő szárú háromszög, ALM∢=20∘, ezért LM és AB párhuzamosak, és az L, M, N pontok egy egyenesbe esnek. LNBA egyenlő szárú trapéz (LA=NB) és nem húrtrapéz, ezért LNBA paralelogramma, és így LN=1. Az LNC háromszög egyenlő szárú,
NCL∢=NLC∢=180∘-80∘2=50∘.
Továbbá PCL∢=PLC∢ (=30∘), így PL=PC, azaz c+d=a+c, tehát a=d.
 
M6. Ismét szükségünk van a szabályos 18-szög oldalainak felvételére (M, N pontok). Felmérjük RP-re P-n túl PK=c-t, és azt fogjuk igazolni, hogy RK=KB (5. ábra).


 

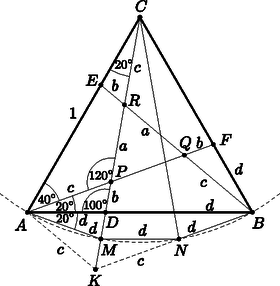5. ábra
 

APK  60∘-os szárszögű egyenlő szárú háromszög, ezért AK=c és AK párhuzamos EB-vel. Így
KAM∢=60∘-40∘=20∘.
Az A és N tükrös helyzetű a KC egyenesre, ezért KN=c, KNM∢=20∘, és így K, N, B egy egyenesre esik. KRB szabályos háromszög (pl. KR=RB és bezárt szögük 60∘), így KR=KB, a+c=c+d, tehát a=d.
 
Megjegyzés. Ha már megkaptuk, hogy K, N, B egy egyenesre esik, akkor a megoldás befejezésére több lehetőség is kínálkozik. Például a KRB háromszög szabályossága abból is következik, hogy szögei 60∘-osak; vagy azt is megmutathatjuk, hogy AKBQ paralelogramma.

 
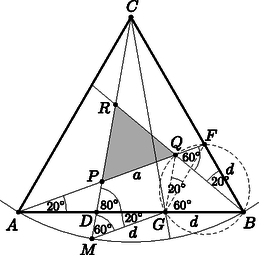
M7. Felvesszük a szabályos 18-szög oldalait és az előző megoldásbeli K pontot. Jelölje AB és CN metszéspontját G (6. ábra). Az MNBG négyszög rombusz, mivel MN és BG oldalai párhuzamosak és egyenlők, és velük azonos hosszúságú az NB oldal is. Így NB=MG=d, valamint NB, MG és AF párhuzamosak (FAB∢=ABN∢=20∘ váltószögek.)


 

6. ábra
 

Azt fogjuk igazolni, hogy QGMP paralelogramma.
A QG szakasz hossza legyen z. Felmérjük AQ-ra Q-n túl QJ=c-t, így a QBJ szabályos háromszöget kapjuk (QJ=QB és a közbezárt szögük 60∘). A GBQ és FBJ háromszögek egybevágók, mert c és d oldalaik 40∘-os szöget zárnak be, így FJ=c-b=z. Mivel az AKM és APD háromszögek egybevágók (megegyezik d és c oldaluk és a közbezárt szögük 20∘), így KM=b, azaz MP=c-b=z szintén. A QGMP négyszög egyenlő szárú trapéz (PQ és MG párhuzamosak, MP=GQ) és nem húrtrapéz, ezért paralelogramma. Így PQ=MG, azaz a=d.
 
Megjegyzések. 1. A megoldás során más utakat is követhetünk, bár ezek elvileg nem nagyon különböznek. Például a QGMP négyszögről szögeinek kiszámításával is igazolhatjuk, hogy paralelogramma. Egy másik lehetőség: a C körüli +60∘-os forgatás a CAP háromszöget a CBJ háromszögbe viszi, ezért CPJ szabályos háromszög. PJ=JC=a+c, és ekkor ráismerhetünk az AKBQ és PKBJ paralelogrammákra: az AQ=a+c, KB=c+d, PJ=a+c szakaszok párhuzamosak és egyenlő hosszúak.
2. A QJB háromszög konstrukciójából és a GBQ és FBJ háromszögek egybevágóságából következik, hogy
GQB∢=FJB∢=180∘-FBJ∢-BFJ∢=60∘.


 
A QJB háromszög konstrukciója nélkül is igazolhatjuk a fenti 2. megjegyzésből adódó segédállítást: az AQB háromszögben QG szögfelező.
 
Bizonyítás: Q-ból párhuzamost húzunk CD-vel, ez AB-t G'-ben metszi, és QG' szögfelezője az AQB szögnek. (Azt kell megmutatnunk, hogy G és G' egybeesik.) Jelölje a szakaszok hosszát QG'=z, G'D=y, G'B=t. Az AG'Q háromszögben yd=ac (párhuzamos szelők tétele), a BDR háromszögben hasonlóan yt=ac. A két egyenletből következik, hogy t=d; azaz G' egybeesik a G szögharmadoló talpponttal.
 
M8. A szabályos 18-szög oldalai és G felvétele után ismét azt igazoljuk, hogy QGMP paralelogramma.
A fenti segédállítás miatt (az AQB háromszögben QG szögfelező) QG és PM párhuzamosak, M7.-ből ismert MG és PQ párhuzamossága. QGMP paralelogramma, így PQ=MG, azaz a=d.
M9. Forgassuk el a C pont körül pozitív irányban 20∘-kal az ACD háromszöget, így az MCG háromszöget kapjuk, ahol MG=AD=d (7. ábra).


 

7. ábra
 

A forgatás szöge és iránya miatt MG és AF párhuzamosak. A BFQG négyszög húrnégyszög, mert az FB szakasz Q-ból és G-ből is 60∘-os szögben látszik (Q és G ugyanabban a félsíkban vannak FB-hez képest). Tehát QGF∢=QBF∢=20∘ (kerületi szögek tétele), vagyis QGB∢=80∘. Emiatt PM párhuzamos QG-vel, így a PMGQ négyszögnek két párhuzamos oldalpárja van, vagyis paralelogramma. Tehát MG=PQ, vagyis a=d.
 
Megjegyzés. Persze ismét követhetünk más utakat is. Például ha már tudjuk, hogy a GBFQ húrnégyszög, akkor ebben az FB=d húrhoz 60∘-os kerületi szög tartozik, így ugyanekkora kerületi szög tartozik a GB=d húrhoz is. Ezért BQG∢=60∘, és PQG∢=60∘ szintén. Innen pedig már következik, hogy PMGQ paralelogramma.