Cím:	Az 58. Nemzetközi Matematikai Diákolimpia feladatainak megoldása, 2. rész
Füzet:	2017/november, 450 - 453. oldal	PDF  |  MathML

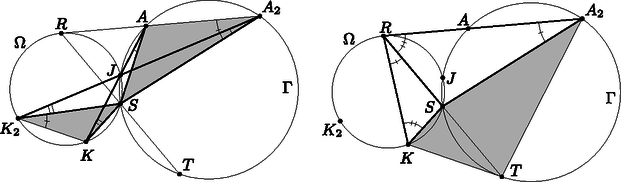
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Második nap1   4. Legyenek $R$ és $S$ különböző pontok egy $\Omega$ körön, amikre $RS$ nem átmérője a körnek. Legyen $\ell$ az $\Omega$ körhöz a $R$ pontban húzott érintőegyenes. Legyen $T$ az a pont, amire teljesül az, hogy $S$ az $RT$ szakasz felezőpontja. Legyen $J$ egy olyan pont az $\Omega$ kör rövidebb $RS$ ívén, amire teljesül az, hogy a $JST$ háromszög $\Gamma$ körülírt köre az $\ell$ egyenest két különböző pontban metszi. Legyen $\Gamma$ és $\ell$ metszéspontjai közül az $A$ pont az, ami közelebb van az $R$-hez. Az $AJ$ egyenes $\Omega$-val vett második metszéspontja legyen $K$. Bizonyítsuk be, hogy a $KT$ egyenes érintője a $\Gamma$ körnek.   Baran Zsuzsanna megoldása. Először is tegyük teljesebbé az ábrát a ,,másik metszéspontok'' felvételével: legyen $l\cap \Gamma =\left\{A\mathrm{,}{A}_2\right\}$ és legyen $A_{2}J\cap \Omega =\left\{J\mathrm{,}{K}_2\right\}$. A megoldás során a szögeket irányítva értelmezzük. A megoldás sok-sok hasonló háromszögpár észrevételén fog alapulni: az $SAK▵\sim S{A}_2{K}_2▵$, a $SA{A}_2▵\sim SK{K}_2▵$, a $RSK▵\sim A_{2}SR▵$, illetve az $SKT▵\sim ST{A}_2▵$ hasonlóságokat fogjuk sorra belátni. [Ezen a ponton érdemes lehet megpróbálni egyénileg befejezni a megoldást.] $J{K}_{2}S\sphericalangle =JKS\sphericalangle$ és $S{A}_{2}J\sphericalangle =SAJ\sphericalangle$ (azonos íven nyugvó kerületi szögek), ezért $SAK▵$ és $S{A}_2{K}_2▵$ szögei megegyeznek, így $SAK▵\sim S{A}_2{K}_2▵$.     Ekkor $\frac{SA}{S{A}_2}=\frac{SK}{S{K}_2}$, továbbá $AS{A}_2\sphericalangle =KS{K}_2\sphericalangle$ (hiszen mindkettő $K_{2}S{A}_2\sphericalangle -K_{2}SA\sphericalangle =KSA\sphericalangle -K_{2}SA\sphericalangle$), emiatt $SA{A}_2▵\sim SK{K}_2▵$. Ekkor $A{A}_{2}S\sphericalangle =K{K}_{2}S\sphericalangle =KRS\sphericalangle$. Az $RA$ érinti $\Omega$-t (és $RS$ elválasztja $A$-t és $K$-t), ezért $ARS\sphericalangle =RKS\sphericalangle$. Így az $RSK▵$ és $A_{2}SR▵$ szögei megegyeznek, ezért $RSK▵\sim A_{2}SR▵$. $TSK\sphericalangle ={180}^{\circ }-KSR\sphericalangle ={180}^{\circ }-RS{A}_2\sphericalangle =A_{2}ST$, továbbá $\begin{array}{c}{\displaystyle \frac{ST}{KS}=\frac{SR}{KS}=\frac{S{A}_2}{RS}=\frac{S{A}_2}{TS}}\end{array}$ (itt kihasználtuk, hogy $S$ az $RT$ szakasz felezőpontja), így $SKT▵\sim ST{A}_2▵$. Ez utóbbi hasonlóságból következik, hogy $STK\sphericalangle =S{A}_{2}T\sphericalangle$, ami éppen azt jelenti, hogy $KT$ érinti a $\Gamma$ kört. Készen vagyunk.   Erre a feladatra sokféle megoldás elképzelhető. Két további megoldási lehetőség címszavakban: (1) Belátjuk, hogy $AT\parallel RK$, majd pedig, hogy $ARXT$ paralelogramma, melyben $S$ az átlók felezőpontja. Itt $X$ a $KST$ kör és az $RK$ egyenes másik metszéspontja. (2) Invertálunk $R$ középponttal, $RS$ sugárral. Belátjuk, hogy a $KT$ egyenes képe és $\Gamma$ képe egymás tükörképei $T\text{'}$-re nézve. Ehhez belátjuk, hogy $RK\text{'}S{A}_2\text{'}$ paralelogramma. Az $RK\text{'}$ és $A_2\text{'}S$ párhuzamossága kijön $RK$ és $AT$ párhuzamosságából.   5. Adott egy $N\ge 2$ egész szám. $N\left(N+1\right)$ futballjátékos, akik között nincs két egyenlő magasságú, valahogyan felállnak egy sorban. Az edző ki akar hagyni ebből a sorból $N\left(N-1\right)$ játékost úgy, hogy a megmaradt $2N$ játékos alkotta sor játékosaira teljesüljön az alábbi $N$ feltétel: $\left(1\right)$ senki nem áll a legmagasabb és a második legmagasabb játékos között, $\left(2\right)$ senki nem áll a harmadik legmagasabb és a negyedik legmagasabb játékos között, $⋮$ $\left(N\right)$ senki nem áll a két legalacsonyabb játékos között. Bizonyítsuk be, hogy ez mindig megtehető.   Borbényi Márton megoldása. Készítsünk $N$ csoportot az alábbi módon: az első csoportban legyen a sor szerint első $N+1$ ember, a másodikban a második $N+1$ ember, és így tovább. Célunk, hogy minden csoportból pontosan $2$ játékost válasszunk ki, így ők a megmaradó $2N$ embernél egymás mellé kerülnek. A következő algoritmust alkalmazzuk: ‐ elkezdjük jelölgetni a játékosokat magasság szerint csökkenő sorrendben; ‐ amint egy csoportban van két kijelölt focista, megállunk; ‐ elhagyjuk ebből a csoportból a két kijelölt játékoson kívül az összes embert, és minden más csoportból a csoport legmagasabb emberét; ‐ a két megjelölt játékossal már nem kell foglalkoznunk, hiszen a megmaradtak között ők ketten a legmagasabbak, és senki nem áll már közöttük; marad $N-1$ csoportunk, mindegyikben $N$ focistával; ‐ ismételjük a fenti eljárást az eggyel kisebb létszámú, eggyel kevesebb csoportból álló sorra stb.   6. Egy egész számokból álló $\left(x\mathrm{,}y\right)$ rendezett párt primitív rácspontnak nevezünk, ha $x$ és $y$ legnagyobb közös osztója 1. Ha adott primitív rácspontok egy véges $S$ halmaza, bizonyítsuk be, hogy van olyan $n$ pozitív egész, és vannak olyan $a_0\mathrm{,}{a}_1\mathrm{,}\text{...}\mathrm{,}{a}_n$ egészek, hogy minden $\left(x\mathrm{,}y\right)$  $S$-beli pontra teljesül $\begin{array}{c}{\displaystyle a_0{x}^n+a_1{x}^{n-1}y+a_2{x}^{n-2}{y}^2+\text{...}+a_{n-1}x{y}^{n-1}+a_n{y}^n=1.}\end{array}$   Williams Kada megoldása. Szeretnénk tehát egy olyan egész együtthatós nemkonstans homogén $f\left(x\mathrm{,}y\right)$ polinomot találni, amire $f\left(x\mathrm{,}y\right)=1$, ha $\left(x\mathrm{,}y\right)\in S$. (Homogénnek nevezünk egy többváltozós polinomot, ha benne minden tag fokszáma egyenlő.) Az $f\left(x\mathrm{,}y\right)$ polinom létezését $|S|$ szerinti indukcióval igazoljuk. Ehhez felhasználjuk az ún. Bézout-lemmát, ami szerint bármely $x$ és $y$ egész számok legnagyobb közös osztója előállítható $ax+by$ alakban, ahol $a\mathrm{,}b\in \text{Z}$. Az $|S|=1$ esetből indulunk ki: ha $S=\left\{\left(x\mathrm{,}y\right)\right\}$, akkor a Bézout-lemma szerint alkalmas $a\mathrm{,}b\in \text{Z}$-re $f\left(x\mathrm{,}y\right)=ax+by$ megfelel. Tegyük fel ezután, hogy az $S=\left\{\left(a_1\mathrm{,}{b}_1\right)\mathrm{,}\text{...}\mathrm{,}\left(a_m\mathrm{,}{b}_m\right)\right\}$ halmaz minden pontján $g\left(x\mathrm{,}y\right)=1$, és szeretnénk az $\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)$ elemet hozzácsatolni. A Bézout-lemma szerint $A{a}_{m+1}+B{b}_{m+1}=1$ alkalmas $A\mathrm{,}B\in \text{Z}$-re. Mivel a $\begin{array}{c}{\displaystyle h\left(x\mathrm{,}y\right)=\prod _{i=1}^m\left(a_{i}y-b_{i}x\right)}\end{array}$ polinom értéke minden $S$-beli pontban $0$, azért $C\mathrm{,}K\in \text{Z}$-re az $\begin{array}{c}{\displaystyle f\left(x\mathrm{,}y\right)=g{\left(x\mathrm{,}y\right)}^K-C\cdot {\left(Ax+By\right)}^{K\cdot \text{deg}g-m}h\left(x\mathrm{,}y\right)}\end{array}$ homogén polinom értéke minden $S$-beli pontban $1$ (feltesszük, hogy $K\ge m$), míg $\begin{array}{c}{\displaystyle f\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)=g{\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)}^K-C\cdot \underset{=:M}{\overset{}{\underbrace{h\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)}}}\mathrm{.}}\end{array}$ Azt állítjuk, hogy $g\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)$ és $M=h\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)$ egymáshoz relatív prím. Valóban, ha lenne közös $p$ prímosztójuk, akkor $p\mid m$ miatt $p$ osztója lenne az $M$ valamelyik $a_i{b}_{m+1}-b_i{a}_{m+1}$ tényezőjének ($1\le i\le m$). Vegyük észre, hogy ekkor a homogenitás miatt ${\displaystyle \begin{array}{cc}\hfill {\displaystyle b_i^{\text{deg}g}g\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)}& {\displaystyle =g\left(b_i{a}_{m+1}\mathrm{,}{b}_i{b}_{m+1}\right)\equiv g\left(a_i{b}_{m+1}\mathrm{,}{b}_i{b}_{m+1}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =b_{m+1}^{\text{deg}g}g\left(a_i\mathrm{,}{b}_i\right)=b_{m+1}^{\text{deg}g}\left(\text{mod}p\right)\mathrm{,}}\hfill \end{array}}$ s így $p\mid g\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)$-ből $p\mid b_{m+1}$ következik. Hasonlóan kapjuk, hogy $p\mid a_{m+1}$. Ez viszont ellentmond annak, hogy $a_{m+1}$ és $b_{m+1}$ relatív prím. Ha $M\ne 0$, akkor a relatív prímség miatt $g{\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)}^{\phi \left(|M|\right)}\equiv 1\left(\text{mod}M\right)$ az Euler‐Fermat-tétel szerint, így pl. $K=m\phi \left(|M|\right)$ választással alkalmas $C\in \text{Z}$-re $f\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)=1$ biztosítható. Ha pedig $M=0$, akkor a $0$-hoz való relatív prímség miatt $g\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)=\pm 1$, s így $K=2$ és $C=0$ megfelel. Tehát minden esetben biztosítottuk, hogy $f\left(a_{m+1}\mathrm{,}{b}_{m+1}\right)=1$ is teljesüljön. Tehát az indukciós lépést befejeztük, az indukció teljes.   Megjegyzés. A feladat általánosítása volt a 2017. szeptemberi számban megjelent A. 703. feladat. Egy további megoldási módszer olvasható a https://www.komal.hu/verseny/feladat.cgi?a=feladat&f=A703&l=hu címen. 1Az első nap feladatainak megoldását az októberi számban közöltük.