Cím:	Megoldásvázlatok a 2017/6. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Koncz Levente
Füzet:	2017/október, 403 - 411. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Egy gyorsvonat két város közötti útját a menetrend szerint 80 km/h átlagsebességgel szokta megtenni. A vonat azonban egyik nap ‐ pályafelújítási munkák miatt ‐ az útja első egyharmadán csak 40 km/h átlagsebességet ért el. Az út második kétharmad részét a menetrend szerint előírt 80 km/h átlagsebességgel tette meg. Az út befejező egyharmad részén ‐ hogy csökkentse a késést ‐ gyorsított, így ezt a szakaszt 100 km/h átlagsebességgel tette meg. A célállomásra így is $12$ perc késéssel érkezett. Hány km a távolság a két város között? $b)$ Egy vasúti jegy árát először $p$ százalékkal felemelték, majd később $2p$ százalékkal csökkentették. Így a jegy eredeti árához képest végül 19,5 százalékkal olcsóbb lett. Határozzuk meg $p$ értékét.  (13 pont)   Megoldás. $a)$ A két város közti távolságot jelölje $s$. Az adatok alapján a következő egyenlet írható fel (a távolságokat km-ben, az időt órában, a sebességet km/h-ban mérjük): $\begin{array}{c}{\displaystyle \frac{s}{80}+0\mathrm{,}2=\frac{\frac{1}{3}s}{40}+\frac{\frac{1}{3}s}{80}+\frac{\frac{1}{3}s}{100}\mathrm{.}}\end{array}$ 1200-zal beszorozva az egyenletet: $\begin{array}{c}{\displaystyle 15s+240=10s+5s+4s\mathrm{,}}\end{array}$ ahonnan $s=60$, a két város távolsága tehát 60 km. Ellenőrzés: A vonat a menetrend szerinti 80 km/h átlagsebességgel 45 perc alatt teszi meg a két város közti utat. Ezen az úton az első 20 km-t (40 km/h átlagsebességgel) 30 perc, a második 20 km-t (80 km/h átlagsebességgel) 15 perc, az utolsó 20 km-t pedig (100 km/h átlagsebességgel) 12 perc alatt tette meg, így összesen valóban 12 perc késéssel (57 perc alatt) ért a célállomásra. $b)$ Az adatok alapján felírható egyenlet a jegy árának változására: $\begin{array}{c}{\displaystyle \left(1+\frac{p}{100}\right)\left(1-\frac{2p}{100}\right)=0\mathrm{,}805.}\end{array}$ 10 000-rel beszorozva és rendezve: $\begin{array}{c}{\displaystyle 0=2p^2+100p-1950.}\end{array}$ Ennek a másodfokú egyenletnek a gyökei $p_1=15$ és $p_2=-65$. A negatív gyök nem ad megoldást, tehát $p=15$. Ellenőrzés: Egy 15 százalékos emelés után egy 30 százalékos csökkentés $1\mathrm{,}15\cdot 0\mathrm{,}7=0\mathrm{,}805$-szeresére változtatja az eredeti árat, ami valóban 19,5 százalékos csökkenésnek felel meg.   2. $a)$ Határozzuk meg az ${\left(x+1\right)}^2{\left(2+cx\right)}^4$ kifejezésben $c$ értékét, ha a műveletek elvégzésével nyert polinomban az elsőfokú tag együtthatója $-64$. $b)$ Határozzuk meg az $A$, $B$ és $C$ kijelentések lehetséges logikai értékeit, ha tudjuk, hogy az $\left(A^B\right)\to \left(\neg B\vee C\right)$ állítás logikai értéke hamis.  (13 pont)   Megoldás. $a)$ ${\left(x+1\right)}^2=x^2+2x+1$. Elsőfokú tagot kapunk, ha az innen kapott $2x$-et szorozzuk a ${\left(2+cx\right)}^4$ hatvány konstans tagjával, vagy az innen kapott 1-et szorozzuk a hatvány elsőfokú tagjával. A binomiális tétel szerint ${\left(a+b\right)}^4=a^4+4a^{3}b+6a^2{b}^2+4a{b}^3+b^4$, tehát $\begin{array}{c}{\displaystyle {\left(2+cx\right)}^4=16+4\cdot 8\cdot cx+6\cdot 4\cdot c^2{x}^2+\text{...}\mathrm{.}}\end{array}$ Ezért a szorzatban az elsőfokú tag együtthatója $2\cdot 16+1\cdot 32c=32+32c=-64$, ahonnan $c=-3$. $b)$ A következtetés akkor és csak akkor hamis, ha az előzmény igaz és a következmény hamis. Tehát $\left(A^B\right)=i$-nek és $\left(\neg B\vee C\right)=h$-nak kell egyszerre teljesülnie. Ha $\left(A^B\right)=i$, akkor az $A$ és $B$ kijelentések logikai értéke is igaz. Ha $B=i$, akkor $\neg B=h$. $\left(\neg B\vee C\right)=h$ akkor teljesül, ha $\neg B$ és $C$ logikai értéke is hamis. Már láttuk, hogy $\neg B=h$, ezért kell, hogy $C=h$ is teljesüljön. A feladatban szereplő következtetés logikai értéke tehát egyetlen esetben lesz hamis: $A=i$, $B=i$, $C=h$.   3. $a)$ Három teljes gráf közül az elsőnek $5$-tel kevesebb, a másodiknak $6$-tal több pontja van, mint a harmadiknak. A két kisebb pontszámú gráfnak együtt összesen annyi éle van, mint a legnagyobb pontszámúnak. Határozzuk meg a három teljes gráf pontjainak számát. $b)$ Egy gráfban cseresznyének nevezzük a két egymáshoz csatlakozó élből álló részgráfot. Igazoljuk, hogy egy hétpontú teljes gráfban a cseresznyék száma megegyezik a négypontú körök számával.  (13 pont)   Megoldás. $a)$ A legkisebb pontszámú gráf pontjainak számát $k$-val jelölve a megoldandó egyenlet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{k\left(k-1\right)}{2}+\frac{\left(k+5\right)\left(k+4\right)}{2}}& {\displaystyle =\frac{\left(k+11\right)\left(k+10\right)}{2}\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(k^2-k\right)+\left(k^2+9k+20\right)}& {\displaystyle =k^2+21k+\mathrm{110,}}\hfill \\ \hfill {\displaystyle k^2-13k-90}& {\displaystyle =\mathrm{0,}}\hfill \end{array}}$ $k=18$ vagy $k=-5$. Ez utóbbi nem megoldása a feladatnak. A három teljes gráfnak 18, 23, illetve 29 pontja van. Ellenőrzés: $K_{18}$-nak 153, $K_{23}$-nak 253, $K_{29}$-nek 406 éle van, és valóban $153+253=406$. $b)$ I. megoldás. Egy cseresznye három pontját $\left(\genfrac{}{}{0ex}{}{7}{3}\right)=35$-féleképpen választhatjuk ki. A három pont közül 3-féleképpen választható ki a cseresznye csúcsa. A hétpontú teljes gráfban a cseresznyék száma tehát $35\cdot 3=105$. Egy négypontú kör pontjait $\left(\genfrac{}{}{0ex}{}{7}{4}\right)=35$-féleképpen választhatjuk ki. Négy adott pont esetén 3-féleképpen választhatjuk ki azt, hogy közülük melyik 2‐2 pont legyen a körben ,,szemben''. A négypontú körök száma tehát $35\cdot 3=105$. $K_7$-ben tehát valóban megegyezik a cseresznyék és a négypontú körök száma. II. megoldás. Kölcsönösen egyértelmű hozzárendelést adunk a hétpontú teljes gráfban található cseresznyék és a négypontú körök között. Számozzuk meg a gráf csúcsait 1-től 7-ig. Egy tetszőlegesen kiválasztott négypontú kör pontjai legyenek $1\le a<b<c<d\le 7$, a körben nem szereplő pontok pedig $1\le e<f<g\le 7$. Három olyan négypontú kör van, mely az $a$, $b$, $c$, $d$ pontokat tartalmazza ($abcda$, $abdca$ és $acbda$), és három cseresznye, mely az $e$, $f$, $g$ pontokat tartalmazza ($efg$, $egf$ és $gef$). Ezt a 3-3 kört és cseresznyét rendre feleltessük meg egymásnak. Ezzel minden négypontú körhöz pontosan egy cseresznyét, és minden cseresznyéhez pontosan egy kört rendeltünk, tehát a négypontú körök és a cseresznyék száma valóban egyenlő.   4. Egy nyolc valós számból álló adatsor öt eleme ismert: 5; 5,5; 10; 12,5 és 15,5. A maradék három elem elveszett, de tudjuk, hogy legalább az egyik egész szám, és a három elem közül kettő egyforma volt. Azt is tudjuk, hogy a teljes adatsor átlaga 10,5, szórása pedig 3,5 volt. Határozzuk meg a hiányzó három elem értékét.  (12 pont)   Megoldás. Legyen a hiányzó elemek értéke $a$, $a$ és $b$. Ekkor az átlag alapján $\frac{5+5\mathrm{,}5+10+12\mathrm{,}5+15\mathrm{,}5+2a+b}{8}=10\mathrm{,}5$, ahonnan $2a+b=35\mathrm{,}5$. A szórás alapján ${\displaystyle \begin{array}{c}\hfill {\displaystyle \sqrt[]{\frac{{\left(5-10\mathrm{,}5\right)}^2+{\left(5\mathrm{,}5-10\mathrm{,}5\right)}^2+{\left(10-10\mathrm{,}5\right)}^2+{\left(12\mathrm{,}5-10\mathrm{,}5\right)}^2+{\left(15\mathrm{,}5-10\mathrm{,}5\right)}^2+2{\left(a-10\mathrm{,}5\right)}^2+{\left(b-10\mathrm{,}5\right)}^2}{8}}=}\hfill \\ \hfill {\displaystyle =\sqrt[]{\frac{84\mathrm{,}5+2{\left(a-10\mathrm{,}5\right)}^2+{\left(b-10\mathrm{,}5\right)}^2}{8}}=3\mathrm{,}\mathrm{5,}}\hfill \end{array}}$ ahonnan $2{\left(a-10\mathrm{,}5\right)}^2+{\left(b-10\mathrm{,}5\right)}^2=13\mathrm{,}5$. ahonnan $2{\left(a-10\mathrm{,}5\right)}^2+{\left(b-10\mathrm{,}5\right)}^2=13\mathrm{,}5$. Az első egyenletből $b=\left(35\mathrm{,}5-2a\right)$-t ebbe behelyettesítve: $\begin{array}{c}{\displaystyle 2{\left(a-10\mathrm{,}5\right)}^2+{\left(25-2a\right)}^2=13\mathrm{,}5.}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle 6a^2-142a+832=0.}\end{array}$ Ennek megoldásai: $a_1=13$ és $a_2=\frac{32}{3}$, melyekhez tartozó $b$ értékek rendre $b_1=9\mathrm{,}5$ és $b_2=\frac{85}{6}$. A második esetben nem kapunk megoldást, mert a három hiányzó érték egyike sem egész szám, tehát a hiányzó három adat 13, 13 és 9,5. Ellenőrzés: a nyolc számból álló adatsor átlaga valóban 10,5, szórása pedig valóban 3,5.   II. rész     5. $a)$ Egy háromszög egyik oldala 7 cm hosszú, az egyik ezen fekvő szög $18$ fokos, az oldallal szemközti szög pedig $108$ fokos. Határozzuk meg a háromszög területét és a háromszögbe írható kör sugarát. 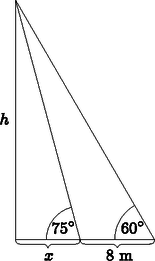$b)$ Egy vízszintes terepen álló torony talppontját megközelíteni nem tudjuk. A torony magasságára árnyékának hosszából szeretnénk következtetni, de a torony megközelíthetetlensége miatt az árnyék pontos hosszát sem tudjuk megmérni. Ezért megjelöljük a torony árnyékának végpontját akkor, amikor a Nap sugarai ${75}^{\circ }$-os szögben érik a talajt. Néhány órával később, amikor a Nap sugarai már csak ${60}^{\circ }$-os szögben érik a talajt, a torony árnyékát ennél $8$ méterrel hosszabbnak találjuk. Milyen magas a torony?  (16 pont)   Megoldás. $a)$ Jelölje a háromszög 18 fokos szöggel szemközti oldalát $a$, az 54 fokos szöggel szemközti oldalát pedig $b$. A háromszög ismeretlen oldalainak hosszát szinusztétellel határozzuk meg: A háromszög területe: $\begin{array}{c}{\displaystyle T=\frac{7\cdot a\cdot \text{sin}{54}^{\circ }}{2}\approx 6\mathrm{,}44\text{c<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>2</mn></mrow></msup></mrow></math> }}\end{array}$ ($a$ két tizedesjegyre kerekített értékével számolva 6,43 cm${}^2$). A beírható kör $r$ sugara a $T=rs$ képlet segítségével határozható meg, ahol $s=\frac{K}{2}\approx 7\mathrm{,}61$ cm. Innen $r=\frac{T}{s}\approx 0\mathrm{,}85$ cm. $b)$ Jelölje a torony magasságát $h$, árnyékának hosszát az első mérés alkalmával $x$. ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{tg}{75}^{\circ }=\frac{h}{x}\text{és}\text{tg}{60}^{\circ }=\frac{h}{x+8}\mathrm{,}}\hfill \\ \hfill {\displaystyle h=\text{tg}{75}^{\circ }\cdot x=\text{tg}{60}^{\circ }\cdot \left(x+8\right)\mathrm{.}}\hfill \end{array}}$ Ebből (kihasználva, hogy $\text{tg}{75}^{\circ }=2+\sqrt[]{3}$), $\begin{array}{c}{\displaystyle x=\frac{8\cdot \text{tg}{60}^{\circ }}{\text{tg}{75}^{\circ }-\text{tg}{60}^{\circ }}\left(=4\sqrt[]{3}\right)\approx 6\mathrm{,}9\text{ méter,}}\end{array}$ majd $h=\text{tg}{75}^{\circ }\cdot x\left(=12+8\sqrt[]{3}\right)\approx 25\mathrm{,}9$ méter.     Másképp: $\begin{array}{c}{\displaystyle x=\frac{h}{\text{tg}{75}^{\circ }}\mathrm{,}\text{majd ezzel}\text{tg}{60}^{\circ }=\frac{h}{\frac{h}{\text{tg}{75}^{\circ }}+8}\mathrm{.}}\end{array}$ Ebből $\begin{array}{c}{\displaystyle h=\frac{8\cdot \text{tg}{60}^{\circ }}{1-\frac{\text{tg}{60}^{\circ }}{\text{tg}{75}^{\circ }}}\left(=12+8\sqrt[]{3}\right)\approx 25\mathrm{,}9\text{ méter.}}\end{array}$   6. Öt osztálytárs: Anna, Balázs, Cili, Dénes és Elemér négynapos közös nyaralásra mennek. Mind a négy napon sorsolással választják ki maguk közül azt az egy embert, akinek aznap reggel be kell vásárolnia (egy-egy emberre akár többször is sor kerülhet). $a)$ Mekkora annak a valószínűsége, hogy mind a négy napon más-más ember megy bevásárolni? $b)$ Mekkora annak a valószínűsége, hogy mind a négy napon ugyanannak az embernek kell bevásárolnia? $c)$ Mekkora annak a valószínűsége, hogy Annát a négy nap alatt legalább kétszer kisorsolják? $d)$ Mekkora annak a valószínűsége, hogy a nyaralás során két ember intézi mind a négy bevásárlást (mindkettőre legalább egyszer sor kerül)?  (16 pont)   Megoldás. $a)$ A kérdezett valószínűséget a kedvező esetek és az összes eset számának hányadosaként kapjuk: $\begin{array}{c}{\displaystyle p=\frac{5\cdot 4\cdot 3\cdot 2}{5^4}=0\mathrm{,}192.}\end{array}$ $b)$ Annak a valószínűsége, hogy pl. Annát sorsolják ki mind a négy napon, ${\left(\frac{1}{5}\right)}^4$. Mivel bármelyik osztálytárs esetén ugyanennyi ez a valószínűség, és ezek egymást kizáró események, ezért $\begin{array}{c}{\displaystyle p=5\cdot {\left(\frac{1}{5}\right)}^4=\frac{1}{125}=0\mathrm{,}008.}\end{array}$ Másképp: Az első nap bárkit kisorsolhatnak. Annak a valószínűsége, hogy a hátralevő három napon is ugyanezt az embert fogják kisorsolni: $\begin{array}{c}{\displaystyle p={\left(\frac{1}{5}\right)}^3=\frac{1}{125}=0\mathrm{,}008.}\end{array}$ $c)$ Binomiális eloszlást használunk. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle P\left(\text{legalább 2-szer kisorsolják Annát}\right)=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =1-P\left(0\text{-szor}\right)-P\left(\text{1-szer}\right)=1-{\left(\frac{4}{5}\right)}^4-\left(\genfrac{}{}{0ex}{}{4}{1}\right)\left(\frac{1}{5}\right){\left(\frac{4}{5}\right)}^3=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =1-0\mathrm{,}4096-0\mathrm{,}4096=0\mathrm{,}1808\left(=\frac{113}{625}\right)\mathrm{.}}\hfill \end{array}}$ $d)$ Először kiszámítjuk annak a valószínűségét, hogy mind a négy bevásárlásra Annát és Balázst sorsolják ki. A négy bevásárlás közül Anna intézhet egyet, kettőt vagy hármat, a többit pedig Balázs. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(3A\mathrm{,1}B\right)}& {\displaystyle =P\left(1A\mathrm{,3}B\right)=\left(\genfrac{}{}{0ex}{}{4}{3}\right){\left(\frac{1}{5}\right)}^4=\frac{4}{625}=0\mathrm{,}\mathrm{0064,}}\hfill \\ \hfill {\displaystyle P\left(2A\mathrm{,2}B\right)}& {\displaystyle =\left(\genfrac{}{}{0ex}{}{4}{2}\right){\left(\frac{1}{5}\right)}^4=\frac{6}{625}=0\mathrm{,}0096.}\hfill \end{array}}$ Tehát $\begin{array}{c}{\displaystyle P\left(A\text{ és <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>B</mi></math> vásárol minden nap}\right)=\frac{14}{625}=0\mathrm{,}0224.}\end{array}$ Mivel hatféleképpen választható ki az a két ember, aki mind a négy bevásárlást intézi, azért a kérdezett valószínűség az előbbi érték hatszorosa: $\begin{array}{c}{\displaystyle P\left(\text{ketten vásárolnak minden nap}\right)=\frac{84}{625}=0\mathrm{,}1344.}\end{array}$   7. $a)$ Határozzuk meg az $a_n=\frac{4n-1}{n}$ sorozat legnagyobb alsó és legkisebb felső korlátját. $b)$ Egy számtani sorozat első $11$ tagjának összege $660$. A sorozat első tagja, hatodik tagja, és első nyolc tagjának összege (ebben a sorrendben) egy mértani sorozat három egymást követő tagját adja. Határozzuk meg a számtani sorozat első tagját és differenciáját.  (16 pont)   Megoldás. $a)$ $a_n=\frac{4n-1}{n}=4-\frac{1}{n}$. Mivel az $\frac{1}{n}$ sorozat szigorúan monoton csökken és 0-hoz tart, ezért az $a_n=4-\frac{1}{n}$ sorozat szigorúan monoton nő és 4-hez tart, tehát legkisebb felső korlátja a 4, legnagyobb alsó korlátja pedig az első tagja: $a_1=4-\frac{1}{1}=3$. $b)$ Az első 11 tag összege: $\frac{\left(2a_1+10d\right)\cdot 11}{2}=660$, innen $\begin{array}{c}{\displaystyle 2a_1+10d=\mathrm{120,}}\end{array}$ (1) azaz $a_1=60-5d$. A mértani sorozatból: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \frac{a_1+5d}{a_1}=\frac{\frac{\left(2a_1+7d\right)\cdot 8}{2}}{a_1+5d}\mathrm{,}}\hfill \\ \hfill {\displaystyle a_1^2+10a_{1}d+25d^2=8a_1^2+28a_{1}d\mathrm{,}}\hfill \\ \hfill {\displaystyle 0=7a_1^2+18a_{1}d-25d^2\mathrm{.}}\hfill \end{array}}$ $\left(*\right)$ Az $a_1$-re kapott összefüggést ide beírva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0}& {\displaystyle =7{\left(60-5d\right)}^2+18\left(60-5d\right)d-25d^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\left(25200-4200d+175d^2\right)+\left(1080d-90d^2\right)-25d^2=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =60d^2-3120d+25200=60\left(d^2-52d+420\right)\mathrm{.}}\hfill \end{array}}$ Innen $d=10$ vagy 42. Ellenőrzés: Az első esetben $a_1=10$, $a_6=60$ és $S_8=360$ valóban egy mértani sorozat ($q=6$) három szomszédos tagja, továbbá $S_{11}=660$. A második esetben $a_1=-150$, $a_6=60$ és $S_8=-24$ szintén valóban egy mértani sorozat ($q=-0\mathrm{,}4$) három szomszédos tagja, továbbá $S_{11}=660$. II. megoldás a $\left(*\right)$-gal jelölt résztől kezdve: $d^2$-tel osztva legyen $c=\frac{a_1}{d}$, ezzel $0=7c^2+18c-25$. Innen $c=1$ vagy $-\frac{25}{7}$, azaz $a_1=d$ vagy $a_1=-\frac{25}{7}d$. Ezt visszaírva az (1) egyenletbe: ${\displaystyle \begin{array}{ccc}{\displaystyle \text{ vagy <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>10</mn><mi>d</mi><mo stretchy="false">=</mo><mn>12</mn><mi>d</mi><mo stretchy="false">=</mo><mn>120</mn></math>, }}\hfill & {\displaystyle \text{ ahonnan <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi><mo stretchy="false">=</mo><mn>10</mn></math> }}\hfill & {\displaystyle \text{ és <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mn>10</mn></math>;}}\hfill \\ {\displaystyle \text{ vagy <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>2</mn><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>10</mn><mi>d</mi><mo stretchy="false">=</mo><mrow><mfrac><mrow><mn>20</mn></mrow><mrow><mn>7</mn></mrow></mfrac></mrow><mi>d</mi><mo stretchy="false">=</mo><mn>120</mn></math>, }}\hfill & {\displaystyle \text{ ahonnan <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>d</mi><mo stretchy="false">=</mo><mn>42</mn></math> }}\hfill & {\displaystyle \text{ és <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">=</mo><mo stretchy="false">-</mo><mn>150</mn></math>. }}\hfill \end{array}}$ III. megoldás: Az első 11 tag összegéből kapjuk, hogy $a_1+5d=60$, ez éppen a számtani sorozat 6. tagja. Ezzel a mértani sorozatból: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{60}{60-5d}}& {\displaystyle =\frac{\frac{\left(120-3d\right)\cdot 8}{2}}{60}\mathrm{,}}\hfill \\ \hfill {\displaystyle 3600}& {\displaystyle =\left(60-5d\right)\left(480-12d\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle 0}& {\displaystyle =60d^2-3120d+25200=60\left(d^2-52d+420\right)\mathrm{.}}\hfill \end{array}}$ Innen pedig az 1. megoldásnál látottak szerint folytatható a gondolatmenet.   8. $a)$ Határozzuk meg $n$ értékét úgy, hogy az alábbi egyenlőség teljesüljön: $\begin{array}{c}{\displaystyle \underset{2}{\overset{n}{\int }}2x+5\text{d}x=\underset{1}{\overset{7}{\int }}10n-2x-3x^2\text{d}x\mathrm{.}}\end{array}$ $b)$ Mekkora területű síkidomot vág ki az $f\left(x\right)=\frac{4}{{\left(x+1\right)}^2}-1$ függvény grafikonja az első síknegyedből? $c)$ Írjuk fel az $f$ grafikonjához az $1$ abszcisszájú pontjában húzott érintőegyenes egyenletét.  (16 pont)   Megoldás. $a)$ Elvégezzük az egyenlet két oldalán kijelölt integrálásokat a Newton‐Leibniz-tétel alapján: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left[x^2+5x\right]}_2^n}& {\displaystyle ={\left[10nx-x^2-x^3\right]}_1^7\mathrm{,}}\hfill \\ \hfill {\displaystyle \left(n^2+5n\right)-\left(4+10\right)}& {\displaystyle =\left(70n-49-343\right)-\left(10n-1-1\right)\mathrm{,}}\hfill \\ \hfill {\displaystyle n^2-55n+376}& {\displaystyle =0.}\hfill \end{array}}$ Innen $n_1=47$ vagy $n_2=8$. Mindkét $n$-re valóban teljesül az egyenlőség: az első esetben 2430, a második esetben pedig 90 az integrálok értéke az egyenlet mindkét oldalán. $b)$ Megkeressük, hogy az $f$ grafikonja hol metszi az $x$ tengely pozitív félegyenesét: $\frac{4}{{\left(x+1\right)}^2}-1=0$, ebből (az $x>0$ feltétel mellett) $x=1$. Mivel az $f$ grafikonja az $y$ tengelyt metszi ($+3$-ban), ezért az első síknegyedből levágott síkidom területét az $\begin{array}{c}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{4}{{\left(x+1\right)}^2}-1\text{d}x}\end{array}$ integrál értéke adja meg: $\begin{array}{c}{\displaystyle T=\underset{0}{\overset{1}{\int }}\frac{4}{{\left(x+1\right)}^2}-1\text{d}x={\left[-\frac{4}{x+1}-x\right]}_0^1=\left(-3\right)-\left(-4\right)=1.}\end{array}$ A kérdéses síkidom tehát éppen egységnyi területű. $c)$ Az érintőegyenes meredekségét az $f$ deriváltfüggvényének az $x=$ 1-ben felvett értéke adja: $\begin{array}{c}{\displaystyle f\text{'}\left(x\right)=-\frac{8}{{\left(x+1\right)}^3}\mathrm{,}\text{tehát}f\text{'}\left(1\right)=-1.}\end{array}$ Az 1 abszcisszájú pont második koordinátája: $\begin{array}{c}{\displaystyle f\left(1\right)=\frac{4}{{\left(1+1\right)}^2}-1=0.}\end{array}$ Az érintőegyenes egyenlete $y=1-x$.   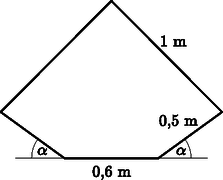9. Egy villanymozdony áramszedőjét két ponton rögzítették a mozdony tetejéhez, ezek távolsága 0,6 méter. Az áramszedő négy, egymáshoz csatlakozó egyenes szakaszból áll. A két rövidebb szakasz 0,5 méter, a két hosszabb szakasz $1$ méter hosszú (lásd az ábrát). Az áramszedő egyes szakaszai a mozdony tetejéhez és egymáshoz képest csuklósan szabadon elmozdulhatnak. Jelölje $h\left(\alpha \right)$ az áramszedő legmagasabb pontjának magasságát a mozdony tetejéhez képest akkor, amikor mindkét rövidebb ág $\alpha$ szöget zár be a mozdony tetejének síkjával.     $a)$ Igazoljuk, hogy $h\left(\alpha \right)=\sqrt[]{1-{\left(0\mathrm{,}3+0\mathrm{,}5\text{cos}\alpha \right)}^2}+0\mathrm{,}5\text{sin}\alpha$. $b)$ Milyen magasan lesz az áramszedő legmagasabb pontja $\alpha ={25}^{\circ }$ esetén? $c)$ Mekkora $\alpha$ szög esetén lesz az áramszedő legmagasabb pontja éppen $1$ méter magasságban?  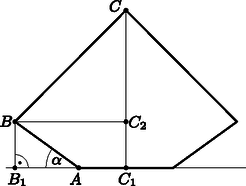(16 pont)   Megoldás. $a)$ Az ábra jelöléseit használjuk.     Az áramszedő egyik rövidebb ága $AB=0\mathrm{,}5$ (m), ez az $A$ pontban csatlakozik a mozdony tetejéhez. A $B$ pont merőleges vetülete a mozdony tetősíkjára $B_1$. Ekkor $BA{B}_1\sphericalangle =\alpha$, $A{B}_1=0\mathrm{,}5\text{cos}\alpha$, $B{B}_1=0\mathrm{,}5\text{sin}\alpha$. Az áramszedő hosszabbik ága $BC=1$ (m). A $C$ pont merőleges vetülete a mozdony tetősíkjára $C_1$. A $B$ pont merőleges vetülete a $C{C}_1$ egyenesre $C_2$. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle h\left(\alpha \right)}& {\displaystyle =C{C}_1=C{C}_2+C_2{C}_1=\sqrt[]{1-C_2{B}^2}+B{B}_1=\sqrt[]{1-{\left(C_{1}A+A{B}_1\right)}^2}+0\mathrm{,}5\text{sin}\alpha =}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\sqrt[]{1-{\left(0\mathrm{,}3+0\mathrm{,}5\text{cos}\alpha \right)}^2}+0\mathrm{,}5\text{sin}\alpha \mathrm{,}}\hfill \end{array}}$ ami éppen a bizonyítandó volt. $b)$ $\alpha ={25}^{\circ }$ esetén ${\displaystyle \begin{array}{cc}\hfill {\displaystyle h\left(\alpha \right)}& {\displaystyle =\sqrt[]{1-{\left(0\mathrm{,}3+0\mathrm{,}5\text{cos}{25}^{\circ }\right)}^2}+0\mathrm{,}5\text{sin}{25}^{\circ }\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx \sqrt[]{1-{\left(0\mathrm{,}3+0\mathrm{,}5\cdot 0\mathrm{,}9063\right)}^2}+0\mathrm{,}5\cdot 0\mathrm{,}4226\approx 0\mathrm{,}\mathrm{869,}}\hfill \end{array}}$ tehát ebben az esetben az áramszedő csúcs kb. 87 cm magasan lesz a mozdony tetejéhez képest. $c)$ Megoldandó a $\sqrt[]{1-{\left(0\mathrm{,}3+0\mathrm{,}5\text{cos}\alpha \right)}^2}+0\mathrm{,}5\text{sin}\alpha =1$ egyenlet. A négyzetre emelést elvégezve és átrendezve: $\begin{array}{c}{\displaystyle \sqrt[]{0\mathrm{,}91-0\mathrm{,}3\text{cos}\alpha -\frac{\text{cos}{}^2\alpha }{4}}=1-0\mathrm{,}5\text{sin}\alpha \mathrm{.}}\end{array}$ Emeljük négyzetre most az egyenletet: $\begin{array}{c}{\displaystyle 0\mathrm{,}91-0\mathrm{,}3\text{cos}\alpha -\frac{\text{cos}{}^2\alpha }{4}=1-\text{sin}\alpha +\frac{\text{sin}{}^2\alpha }{4}\mathrm{.}}\end{array}$ Átrendezve: $\begin{array}{c}{\displaystyle \text{sin}\alpha -0\mathrm{,}09-\left(\frac{\text{sin}{}^2\alpha }{4}+\frac{\text{cos}{}^2\alpha }{4}\right)=0\mathrm{,}3\text{cos}\alpha \mathrm{.}}\end{array}$ Kihasználva, hogy $\text{sin}{}^2\alpha +\text{cos}{}^2\alpha =1$, kapjuk, hogy $\text{sin}\alpha -0\mathrm{,}34=0\mathrm{,}3\text{cos}\alpha$. $\left(*\right)$ Ismét négyzetre emelünk: $\begin{array}{c}{\displaystyle \text{sin}{}^2\alpha -0\mathrm{,}68\text{sin}\alpha +0\mathrm{,}1156=0\mathrm{,}09\text{cos}{}^2\alpha \mathrm{.}}\end{array}$ $\text{cos}{}^2\alpha =1-\text{sin}{}^2\alpha$ helyettesítéssel: ${\displaystyle \begin{array}{c}\hfill {\displaystyle 1\mathrm{,}09\text{sin}{}^2\alpha -0\mathrm{,}68\text{sin}\alpha +0\mathrm{,}0256=\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{sin}{\alpha }_{\mathrm{1,2}}\approx \frac{0\mathrm{,}68\pm \sqrt[]{0\mathrm{,}{68}^2-4\cdot 1\mathrm{,}09\cdot 0\mathrm{,}0256}}{2\cdot \mathrm{1,09}}=\frac{0\mathrm{,}68\pm \sqrt[]{0\mathrm{,}350784}}{2\mathrm{,}18}\approx \frac{0\mathrm{,}68\pm 0\mathrm{,}5923}{2\mathrm{,}18}\mathrm{.}}\hfill \end{array}}$ Azaz $\text{sin}\alpha \approx 0\mathrm{,}5836$, tehát $\alpha \approx 35\mathrm{,}{705}^{\circ }$, vagy $\text{sin}\alpha \approx 0\mathrm{,}0402$, tehát $\alpha \approx 2\mathrm{,}{306}^{\circ }$. Ez utóbbi a második négyzetre emelésnél keletkezett hamis gyök (a négyzetre emelés előtt az egyenlet bal oldala negatív, a jobb oldala pozitív). Előbbi érték viszont valóban megoldása a feladatnak, hiszen könnyű meggyőződni róla, hogy ebben az esetben mindkét négyzetre emelésnél az egyenlőség mindkét oldala pozitív. Tehát $\alpha \approx {36}^{\circ }$ esetén lesz a mozdony áramszedőjének csúcsa éppen 1 méter magasan. II. megoldás a $\left(*\right)$-gal jelölt résztől kezdve: $\begin{array}{c}{\displaystyle \text{sin}\alpha -0\mathrm{,}3\text{cos}\alpha =0\mathrm{,}34.}\end{array}$ $\sqrt[]{1^2+0\mathrm{,}{3}^2}=\sqrt[]{1\mathrm{,}09}\left(\approx 1\mathrm{,}044\right)$-gyel osztva: $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{1\mathrm{,}09}}\text{sin}\alpha -\frac{0\mathrm{,}3}{\sqrt[]{1\mathrm{,}09}}\text{cos}\alpha =\frac{0\mathrm{,}34}{\sqrt[]{1\mathrm{,}09}}\mathrm{.}}\end{array}$ Mivel $\frac{1}{\sqrt[]{1\mathrm{,}09}}\approx \text{cos}16\mathrm{,}{699}^{\circ }$ és $\frac{0\mathrm{,}3}{\sqrt[]{1\mathrm{,}09}}\approx \text{sin}16\mathrm{,}{699}^{\circ }$, ezért ez (az ismert addíciós tétel segítségével) így írható: $\begin{array}{c}{\displaystyle \text{sin}\alpha \text{cos}16\mathrm{,}{699}^{\circ }-\text{cos}\alpha \text{sin}16\mathrm{,}{699}^{\circ }=\text{sin}\left(\alpha -16\mathrm{,}{699}^{\circ }\right)=\frac{0\mathrm{,}34}{\sqrt[]{1\mathrm{,}09}}\approx \text{sin}19\mathrm{,}{006}^{\circ }\mathrm{,}}\end{array}$ ahonnan (mivel $\alpha$ hegyesszög) $\alpha -16\mathrm{,}{699}^{\circ }\approx 19\mathrm{,}{006}^{\circ }$, azaz $\alpha \approx 35\mathrm{,}{705}^{\circ }$.