Kezdőlap


Cím:	A középiskolai tanárok versenyének feladatai
Szerző(k):	Csordásné Szécsi Jolán
Füzet:	2017/október, 396 - 399. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A verseny időtartama 90 perc. A feladatok pontozása: minden helyes válasz 5 pontot ér; helytelen válaszra 0 pont, válasz nélkül hagyott kérdésekre 1-1 pont jár. A versenyen íróeszközön, papíron, körzőn és vonalzón kívül semmilyen más segédeszköz nem használható.
1. A 19 az 1 híján 20. Hány híján 20 az 1?
(A) $- 21$ ; (B) $- 20$ ; (C) $- 19$ ; (D) 19; (E) 21.
2. Mennyi annak a számrendszernek az alapszáma, amelyben ez a feladatsor 42 feladatból áll? (A) 5; (B) 6; (C) 7; (D) 8; (E) 9.
3. Az $x$ és az $y$ olyan 0-tól különböző valós számok, amelyekre $x - y = x y$ . Mennyi az $\frac{1}{x} - \frac{1}{y}$ különbség?
(A) $- 1$ ; (B) 0; (C) 1; (D) $- \frac{1}{x y}$ ; (E) Az előzőek közül egyik sem.
4. Hány olyan négyzet van, melynek a csúcsai az ábrán látható rácspontok közül kerülnek ki?
(A) 10; (B) 15; (C) 16; (D) 17; (E) 18.¹

5. Hat különböző természetes szám összege 20. Mennyi a hat szám szorzata? (A) 0; (B) 120; (C) 360; (D) 720; (E) Egyértelműen nem határozható meg.

6. Hány olyan állítás van az alábbiak között, amely nem teljesül egyetlen olyan

a

b

és

c

számhármas esetén sem, melyre

a < b < c

\begin{matrix} a + b < c, a + c < b, a \cdot b < c, a \cdot c < b, b : c = a . \end{matrix}

(A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
7. Hány szakaszt határoznak meg azok a derékszögű koordinátarendszerben lévő pontok, amelyeknek mindkét koordinátája egész szám és a két koordináta szorzata 2017? (A) 1; (B) 4; (C) 6; (D) 8; (E) 10.
8. Hány olyan

p

prímszám van, melyre a

[\frac{3 p - 15}{11}] = 3

?
(A) 0; (B) 1; (C) 2; (D) 3; (E) 4.
9. Mennyi a

\frac{2 \cdot 3 \cdot 5 + 4 \cdot 6 \cdot 10 + ... + 100 \cdot 150 \cdot 250}{2 \cdot 4 \cdot 6 + 4 \cdot 8 \cdot 12 + ... + 100 \cdot 200 \cdot 300}

tört?
(A)

\frac{5}{8}

; (B)

\frac{6}{7}

; (C)

\frac{7}{8}

; (D) 1; (E)

\frac{8}{7}

.
10. Melyik az

A

B

és

C

kifejezések értékének növekvő sorrendje, ha

\begin{matrix} A = {(\sqrt[3]{8} + 4^{\frac{3}{2}})}^{\frac{1}{2}}, B = sin^{2} \frac{π}{5} és C = \sqrt[]{3 + \sqrt[]{8}} - \sqrt[]{3 - \sqrt[]{8}} ? \end{matrix}

(A)

A B C

; (B)

B A C

; (C)

B C A

; (D)

C A B

; (E)

C B A

.
11. Hány olyan

n

egész szám van, melyre a

2017^{n} + 2017^{n - 1} + ... + 2017^{2} + 2017 - 1

összeg osztható 2016-tal? (A) 0; (B) 1; (C) 2; (D) 2017; (E) végtelen sok.
12. Öt egymást követő egész szám összege

\bar{1 a b 5 c}

ötjegyű szám. Hány ilyen szám van? (A) 0; (B) 5; (C) 162; (D) 198; (E) 200.
13. Mennyi az

1! + 2! + 3! + ... + 2017!

összeg 2017-dik hatványának az egyes helyiértékén álló számjegye? (A) 1; (B) 3; (C) 7; (D) 8; (E) 9.
14. Egy verseny előtt öt versenyző, Anna, Bea, Cili, Dóri és Emese a következőket állította:

\begin{matrix} Anna: Az első három között végzek a versenyen. \\ Bea: Én nyerek. \\ Cili: Legyőzöm Annát. \\ Dóri: Nem tudom Beát megelőzni. \\ Emese: Cili vagy Dóri lesz az első. \end{matrix}

Mi lett a versenyzők sorrendje, ha egyiküknek sem lett igazuk? (A válaszokban a versenyzőket nevük kezdőbetűivel jelöljük.)
(A)

E C B D A

; (B)

E B D A C

; (C)

E B C D A

; (D)

B D E C A

; (E)

E D B A C

.
15. Egy egyenlő szárú trapéz oldalai 1; 1; 1 és 2 egység hosszúak. Hány egység a trapéz köré írt kör sugara?
(A) 1; (B)

\sqrt[]{2}

; (C) 1,5; (D) 2; (E) Az előzőek közül egyik sem.
16. Hányféleképpen tölthető ki egy

10 \times 10

-es négyzetrács úgy, hogy a négyzetrács minden négyzetébe az 1 vagy a

- 1

számot írjuk, és a sorokban és az oszlopokban álló számok összege különböző? (A) 0; (B) 4; (C) 8; (D) 12; (E) 16.

17. Mennyi

x_{2017}

, ha

x_{1} = \frac{1}{2}

és

x_{n + 1} = \frac{1}{2 - x_{n}}

, ahol

n \in N^{+}

?
(A)

\frac{2016}{2018}

; (B)

\frac{2015}{2017}

; (C)

\frac{2016}{2017}

; (D)

1 - \frac{1}{2018}

; (E) 1.
18. Mennyi az

x + y

összeg, ha

x

és

y

olyan természetes számok, melyekre teljesül az

x^{2} + x = 2^{y} + 1259

egyenlet? (A) 0; (B) 32; (C) 35; (D) 36; (E) 71.
19. Egy négyzet csúcsaihoz számokat írunk, majd kiválasztunk két olyan csúcsot, amelyek egy oldalra illeszkednek, és mindkét csúcsnál lévő számhoz 1-et adunk. Ezután a két csúcs kiválasztását és a csúcsoknál lévő számokhoz az 1 hozzáadását egymás után többször megismételjük. Melyik esetben érhető el, hogy mind a négy csúcsnál ugyanaz a szám legyen?
(A)

; (B)

; (C)

; (D)

; (E)

.
20. Egy húrnégyszög átlói merőlegesek egymásra. Melyik összefüggés igaz a két szemben fekvő

a

és

c

oldalhossza és a körülírt körének

r

sugara között?
(A)

a^{2} = c r

; (B)

r^{2} = a c

; (C)

c^{2} = a r

; (D)

a^{2} = r^{2} + c^{2}

; (E)

a^{2} = 4 r^{2} - c^{2}

.
21. Egy dobozban piros, zöld és kék golyók vannak. Legkevesebb 6 golyót kell kihúzni a dobozból, hogy biztosan legyen a kihúzott golyók között piros. Legkevesebb 7 golyót kell kihúzni a dobozból, hogy biztosan legyen a kihúzott golyók között zöld. Legkevesebb 8 golyót kell kihúzni a dobozból, hogy biztosan legyen a kihúzott golyók között kék. Hány piros golyó van a dobozban? (A) 4; (B) 5; (C) 6; (D) 7; (E) 8.
22. Hány olyan 2017-nél nem nagyobb pozitív egész szám írható az

n

helyére, hogy a

2^{n} - 1

különbség osztható legyen 7-tel? (A) 0; (B) 1; (C) 672; (D) 673; (E) 2017.
23. Egy kör alakú, tíz részre osztott tábla három részében kezdetben 10 kavics van (lásd ábra). A tábla melletti halomból ráteszünk egyszerre egy-egy kavicsot két egymás melletti részre, majd ezt többször megismételjük azért, hogy mind a tíz részben ugyanannyi kavics legyen. Hány kavics lesz akkor a táblán, amikor mind a tíz részben ugyanannyi lesz, és a táblán a kavicsok száma a lehető legkevesebb? (A) 50; (B) 80; (C) 100; (D) 120; (E) Soha nem lehet ugyanannyi kavics mind a tíz részben.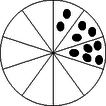

24. Hány olyan

b

természetes szám van, melyre a

b^{4} + 3 b^{2} + 1

és a

b^{3} + 2 b

legnagyobb közös osztója 1?
(A) 0; (B) 1; (C) 2; (D) végtelen sok; (E) Az előzőek közül egyik sem.
25. A Bakancsos túraszakosztály öt túrát szervezett az év során. A szakosztály 50 tagja közül 41-en vettek részt az első, 46-an a második, 43-an a harmadik, 31-en a negyedik és 39-en az ötödik túrán. Hányan vettek részt a szakosztály tagjai közül a negyedik és az ötödik túrán is, ha mind az öt túrán a szakosztály egyetlen tagja sem vett részt? (A) 14; (B) 15; (C) 20; (D) 25; (E) Ezekből az adatokból nem lehet meghatározni.
26. Feri a háromjegyű és négyjegyű páros számokat vizsgálta. Először kiszámolta a vizsgált számok számtani közepét. Utána kiválasztott a számok közül 150-et, és a többi szám számtani közepét is meghatározta. Mennyi a kiválasztott 150 szám összege, ha a két kiszámolt átlag egyenlő?
(A) 100 000; (B) 250 510; (C) 457 030; (D) 700 125; (E) 757 350.
27. Egy nagy kockát ragasztunk össze 27 db szabályos dobókockából, majd a nagy kocka tetszőleges öt lapjának mindegyikéből kivesszük a középső dobókockát. Mennyi lehet az így kapott test felületén látható pöttyök száma, ha az a lehető legkevesebb? (A szabályos dobókocka lapjai 1-től 6-ig pöttyözöttek, és a szemközti lapokon lévő pöttyök számának összege 7.) (A) 187; (B) 194; (C) 208; (D) 210; (E) 215.
28. Egy háromszög egyik oldala

a

, az

a

oldalhoz tartozó magasság

m

. Melyik kifejezés adja meg a háromszög kerületének a lehető legkisebb értékét bármely lehetséges

a

és

m

esetén? (A)

a + 4 m

; (B)

\sqrt[]{a^{2} + m^{2}}

; (C)

\sqrt[]{2 a^{2} + m^{2}}

; (D)

\sqrt[]{4 m^{2} + a^{2}}

; (E)

a + 2 \cdot \sqrt[]{m^{2} + {(\frac{a}{2})}^{2}}

.
29. Egy bogár az

A

pontból indul és egyenes vonal mentén haladva 16 cm megtétele után a

B

pontba érkezik. A

B

pontban az eredeti haladási irányához képest

α

szöggel elfordul, az új irányban szintén egyenes vonalban folytatja útját, és 10 cm megtétele után a

C

pontba érkezik. Mennyi a valószínűsége annak, hogy az

A C

távolság kisebb 14 cm-nél, ha az

α

szöget radiánban mérjük, és véletlenszerűen választjuk ki a

] 0; π [

intervallumból? (A)

\frac{1}{5}

; (B)

\frac{1}{4}

; (C)

\frac{1}{3}

; (D)

\frac{2}{5}

; (E)

\frac{3}{5}

.
30. Egy téglalap két szomszédos oldalának a hossza 6 cm és 2 cm. A téglalap hosszabb középvonalának

P

egy olyan pontja, amelyből az egyik 2 cm hosszú oldal kétszer akkora szögben látszik, mint a másik 2 cm hosszú oldal. Hány centiméterre lehet a

P

pont a téglalap egyik rövidebb oldalától?
(A)

\frac{\sqrt[]{7}}{3}

; (B)

\frac{\sqrt[]{10}}{3}

; (C)

\frac{1 + \sqrt[]{8}}{2}

; (D)

\sqrt[]{5}

; (E)

\frac{6 + \sqrt[]{39}}{3}

A középiskolai tanárok versenyének eredménye

1‐2. Fonyó Lajos (Keszthelyi Vajda János Gimn.) ..... 150 pont
1‐2. Fridrik Richárd (Szegedi Tudományegyetem) ..... 150 pont
3. Károlyi Gergely (Budapest, Berzsenyi Dániel Gimn.) ..... 140 pont
4. Baloghné Cseh Judit (Szolnok, Varga Katalin Gimn.) ..... 133 pont
5. Kórus Péter (Szeged, SZTE JGYPK TÓKI) ..... 131 pont
6. Fonyóné Németh Ildikó (Keszthelyi Vajda János Gimn.) ..... 125 pont
6. Mahler Attila (Budapest, Berzsenyi Dániel Gimn.) ..... 125 pont
8. ,,bambusz'' ..... 124 pont
9. Nagy Piroska Mária (Dunakeszi, Radnóti Miklós Gimn.) ..... 122 pont
10. Nádháziné Borbola Éva (Kecskemét, Katona József Gimn.) ..... 121 pont.

Az általános iskolai tanárok versenyének² eredménye

1. B. Varga József (Temerin, Petar Kocsity Ált. Isk.) ..... 129 pont
2. Csanády Gáborné (Budapest, Baár-Madas Ref. Ált. Isk. és Gimn.) ..... 125 pont
3. Egyed László (Bajai III. Béla Gimn.) ..... 124 pont
4. Paróczay Eszter (Gödöllői Premontrei Szent Norbert Ált. Isk. és Gimn.) ..... 115 pont
5. ,,Domb'' ..... 107 pont
6. ,,Tomi01'' ..... 99 pont.

¹A helyes válasz 20, mely nem szerepelt a válaszlehetőségek között.

²Az általános iskolai tanárok versenyének feladatait nem közöljük.