Kezdőlap


Cím:	Beszámoló az 1. Európai Fizikai Diákolimpiáról
Szerző(k):	Marozsák Tóbiás , Németh Balázs , Simon Dániel Gábor
Füzet:	2017/szeptember, 365 - 371. oldal	PDF \| MathML
Témakör(ök):	Egyéb (KöMaL pontverseny is)

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

2017. május 20. és 24. között rendezték meg Észtországban az 1. Európai Fizikai Diákolimpiát, röviden EuPhO-t, ahol Magyarország is képviseltette magát. A versenyre való kiválasztás a Kunfalvi Rezső válogatóverseny alapján zajlott, ahonnan a három legjobb eredményt elért, nem végzős diák került a csapatba (a verseny időpontja ugyanis egybeesett az érettségi vizsgák időpontjával). A csapatot két tanár kísérte: Vankó Péter (BME Fizikai Intézet) mint csapatvezető és Vigh Máté (ELTE Fizikai Intézet) mint a javító bizottság tagja.
Maga a verseny Tartu városában zajlott, mely Észtország egyik egyetemi központja. Itt alkalmunk volt megnézni a gyönyörű városközpontot és a történelmi jelentőségű tartui obszervatóriumot. A javítás és az eredményhirdetés a fővárosban, Tallinnban történt, ahol lehetőségünk adódott megtekinteni a fantasztikus óvárost.
A versenyen ‐ a Nemzetközi Diákolimpiához hasonlóan ‐ egy elméleti és egy gyakorlati forduló volt, mindkettő öt órás terjedelemben. A szervezők törekedtek rövid, ötletes feladatok kitűzésére, melyek mellőzték a hosszadalmas számolásokat. Az elméleti fordulóban három feladat volt: az első egy kötél rezgéseit vizsgálta, a második egy termodinamikai probléma volt, míg a harmadik feladat egy szupravezető háló és egy mágneses dipólus kölcsönhatásával foglalkozott. A gyakorlati fordulóban egy LED hatásfokát és $U$ ‐ $I$ karakterisztikáját mérték meg a versenyzők a rendelkezésükre álló eszközökkel.
A csapat és eredményeik (a maximális pontszám 50):

Németh Balázs (24,2 pont) ezüstérem; Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf., felkészítő tanár: Csefkó Zoltán, Dvorák Cecília;

Marozsák Tóbiás (23,0 pont) ezüstérem; Budapest, Óbudai Árpád Gimnázium, 11. évf., felkészítő tanár: Mezei István, Gärtner István;

Simon Dániel Gábor (17,3 pont) bronzérem; Kecskeméti Bányai Júlia Gimnázium, 11. évf., felkészítő tanár: Bakk János.
A versenyen szerzett pozitív tapasztalatok alapján a résztvevők egyetértettek, hogy folytatják az EuPhO szervezését, így ha minden igaz, jövőre Oroszországban, Moszkvában kerül megrendezésre a 2. EuPhO, ahol reményeink szerint ötfős csapat fogja képviselni hazánkat, akár végzős diákok is.
A továbbiakban ismertetjük az elméleti feladatokat, valamint azok hivatalos megoldását.

1. Rezgő kötél

Egy súlyos, állandó vastagságú,

L

hosszúságú kötél függőlegesen lóg a mennyezetről. A kötél rezgéseket végezhet az egyensúlyi helyzete körül különböző sajátfrekvenciákkal, amelyeket növekvő sorrendben így jelölünk:

f_{i}

(

i = 1,2, ...

). Az 1. ábra egy számítógépes szimuláció alapján a kötél alakját mutatja az első három sajátfrekvencián végzett rezgés esetében. Figyelj arra, hogy az ábrán a vízszintes és a függőleges skála nem egyforma. Felteheted, hogy a kötél kitérése sokkal kisebb a hosszánál (kis amplitúdójú közelítés).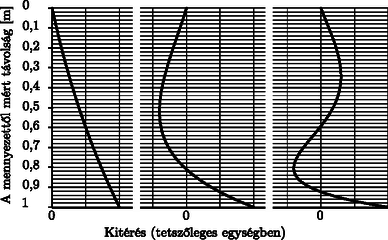

1. ábra

A) Dolgozz ki egy egyszerűsített modellt, amellyel meg tudod becsülni a kötél alaprezgésének

f_{1}

frekvenciáját! Ez alapján számítsd ki közelítőleg

f_{1}

értékét, ha a kötél hossza

L = 1, 0 m

. Számolj

g = 9, 8 {m/s}^{2}

értékkel.
B) Olvasd le a szükséges adatokat az ábráról, és becsüld meg az

f_{1} : f_{2} : f_{3}

frekvenciaarányt!

Megoldás. A) A 2. ábráról leolvasható, hogy az első esetben a kötél görbülete elhanyagolható, vagyis kis kitéréseknél közelíthetünk egy fizikai ingával:

\begin{matrix} f_{1} = \frac{1}{2 π} \sqrt[]{\frac{m g \frac{L}{2}}{θ}} = \frac{1}{2 π} \sqrt[]{\frac{m g \frac{L}{2}}{\frac{1}{3} m L^{2}}} = \frac{1}{2 π} \sqrt[]{\frac{3 g}{2 L}} = 0, 61 Hz . \end{matrix}

2. ábra

B) Dimenzióanalízis segítségével megállapítható, hogy a frekvencia csak

g

-től és

L

-től függhet, méghozzá a következő módon:

\begin{matrix} f_{k} = c_{k} \sqrt[]{\frac{g}{L}} . \end{matrix}

Itt

c_{k}

egy dimenziótlan együttható, mely csupán a

k

módusszámtól függ. Bejelölve a 2. ábrán az

N

pontot világos, hogy az

N

pont kitérése

0

a mozgás során, így az

N B

kötélszakasz közelítőleg a kötél alapfrekvenciáján rezeg. Tehát írhatjuk:

\begin{matrix} f_{2} (L) \equiv f_{1} (N B) = f_{1} (L - N A) . \end{matrix}

Ezáltal:

\begin{matrix} \frac{f_{2} (L)}{f_{1} (L)} = \frac{f_{1} (L - N A)}{f_{1} (L)} = \sqrt[]{\frac{L}{L - N A}} . \end{matrix}

A kötél vízszintes kitérése igen kicsiny a hosszához képest, így mérhetjük az

N A

szakaszt a függőleges tengelyen. Ekkor

N A \approx 0, 8 m

L = 1, 0 m

, tehát:

\begin{matrix} \frac{f_{2}}{f_{1}} \approx 2, 2. \end{matrix}

Hasonló gondolatmenetet alkalmazva mint az előbb, lemérhetjük, hogy

N_{1} A \approx 0, 6 m

\begin{matrix} f_{3} (L) & \equiv f_{2} (L - N_{1} A), \\ \frac{f_{3} (L)}{f_{2} (L)} & = \frac{f_{2} (L - N_{1} A)}{f_{2} (L)} = \sqrt[]{\frac{L}{L - N_{1} A}} \approx 1, 6. \end{matrix}

Ezek szerint

\begin{matrix} \frac{f_{3}}{f_{1}} = \frac{f_{3}}{f_{2}} \cdot \frac{f_{2}}{f_{1}} \approx 3, 5, \end{matrix}

így a végeredmény:

\begin{matrix} f_{1} : f_{2} : f_{3} \approx 1 : 2, 2 : 3, 5. \end{matrix}

2. Korong gázban

Tekintsünk egy vékony, lapos,

M

tömegű,

S

területű, kezdetben

T_{1}

hőmérsékletű korongot, amely kezdetben a súlytalanság állapotában nyugalomban van egy

ϱ

sűrűségű,

T_{0}

hőmérsékletű gázban (

T_{1} = 1000 T_{0}

). A korong egyik oldala hőszigetelő réteggel van bevonva, a másik oldala viszont nagyon jó hőkontaktusban van a környező gázzal: az

m

tömegű gázmolekulák a felülettel történő egyetlen ütközés során elnyerik a korong hőmérsékletét.

Becsüld meg a korong kezdeti

a_{0}

gyorsulását és a kialakuló mozgás során elért

v_{{max}_{}^{}}

maximális sebességét!

Tedd fel, hogy a korong hőkapacitása

N k_{B}

nagyságrendű, ahol

N

a benne lévő atomok száma,

k_{B}

pedig a Boltzmann-állandó, valamint hogy a gáz és a korong anyagának moláris tömege ugyanakkora nagyságrendű. A molekulák átlagos szabad úthossza (az az átlagos távolság, amit egy molekula két ütközés között megtesz) sokkal nagyobb, mint a korong mérete. Hanyagolj el minden, a korong pereménél fellépő széleffektust.

Megoldás. A gáz által a korong hőszigetelő réteggel bevont oldalára kifejtett nyomás kezdetben

P_{0} = n k_{B} T_{0}

, ahol

n

a gáz részecskeszám-sűrűsége. Erre az eredményre a

j_{0} \sim v_{x 0}

részecskeáram, valamint az egy molekula által átadott

p_{0} = 2 m v_{x 0}

impulzus (

v_{x 0}

a molekulák sebességének normál irányú komponense) szorzatának átlagolásával juthatunk (

\bar{2 v_{x 0}^{2}} \sim T_{0}

).
Hasonló gondolatmenetet követve számíthatjuk ki a korong jó hővezető oldalán fellépő nyomást. Itt a részecskeáram-sűrűség az előbbi érték, azonban a molekulánként átadott impulzus nagyobb a teljesen rugalmas ütközés esetéhez képest:

\begin{matrix} p_{1} = m (v_{x 0} + v_{x 1}) \approx m v_{x 1}, \end{matrix}

ahol

v_{x 1}

a kontaktust követően a korongtól távolodó molekulák sebességének a felületre merőleges komponense. Ennélfogva a

P_{1}

nyomásra:

\begin{matrix} \frac{P_{1}}{P_{2}} = \frac{\bar{v_{x 0} v_{x 1}}}{\bar{2 v_{x 0}^{2}}} \approx \frac{\sqrt[]{T_{1} T_{0}}}{T_{0}}, \end{matrix}

ami egy konstans (egy nagyságrendű) szorzótényezőtől eltekintve helyes eredmény.
A korongra ható eredő erő:

\begin{matrix} F = (P_{1} - P_{0}) S \approx S n k_{B} \sqrt[]{T_{0} T_{1}}, \end{matrix}

így a kezdeti gyorsulás:

\begin{matrix} a_{0} \approx \frac{S n k_{B}}{M} \sqrt[]{T_{0} T_{1}} = \frac{S ϱ k_{B}}{m M} \sqrt[]{T_{0} T_{1}} . \end{matrix}

Mivel

P_{1} ≫ P_{0}

, a korong gyorsulni fog egészen addig, amíg a sebessége el nem éri a gázmolekulák sebességének nagyságrendjét. Amikor ez bekövetkezik, azaz a korong

v

sebessége eléri a

v_{0} = \sqrt[]{k T_{0} / m}

nagyságrendet, a hátoldalt érő

j (v)

részecskeáram exponenciális ütemnél is gyorsabban csökkenni kezd, összhangban az ideális gáz molekuláinak sebességeloszlásával (például

j (2 v_{0}) \approx j_{0} 10^{- 3}

, míg

j (3 v_{0}) \approx j_{0} 10^{- 6}

). Hasonló ütemben csökken a korongot előre hajtó

P_{1}

nyomás is, így a korong nem gyorsul tovább. Ennélfogva a korong legnagyobb sebessége:

\begin{matrix} v_{max} \approx v_{0} = \sqrt[]{\frac{k_{B} T_{0}}{m}} . \end{matrix}

Az előzőekben feltettük, hogy a korong nem hűl le jelentősen az említett sebesség eléréséig. Ennek belátásához tekintsük először a hozzávetőleges gyorsulási időt:

\begin{matrix} t_{gy} \approx \frac{v_{max}}{a_{0}} \approx \frac{M \sqrt[]{m k_{B} T_{0}}}{S ϱ k_{B} \sqrt[]{T_{0} T_{1}}} = \frac{M}{ϱ S} / \sqrt[]{\frac{k_{B} T_{1}}{m}} . \end{matrix}

Mivel a hűlést jellemző

P_{h}

teljesítmény a korong indulásakor maximális, felső becslést adhatunk a hűlés idejére

t_{h} = \frac{Q}{P_{h}}

alakban, ahol

Q

a korong teljes hőmennyisége. A

P_{h}

teljesítmény becsült értéke:

\begin{matrix} P_{h} \approx S j_{0} \cdot k_{B} T_{1} \approx S n k_{B} \sqrt[]{T_{0} T_{1}} \sqrt[]{\frac{k_{B} T_{1}}{m}}, \end{matrix}

továbbá a teljes hőmennyiség

Q \approx N k_{B} T_{1}

. Felhasználva, hogy

M \approx N m

, a hűlés idejére a következő adódik:

\begin{matrix} t_{h} \approx \frac{(M / m) k_{B} T_{1}}{S n k_{B} T_{1} \sqrt[]{k_{B} T_{0} / m}} = \frac{M}{ϱ S} / \sqrt[]{\frac{k_{B} T_{0}}{m}} . \end{matrix}

Végül vegyük észre, hogy

t_{gy} / t_{h} \approx \sqrt[]{T_{0} / T_{1}} ≪ 1

, azaz a korong valóban nem hűl le jelentősen a

v_{0}

sebesség elérése előtt.

3. Szupravezető háló

Tekintsünk egy hálót, amely egy lapos szupravezető lapból úgy készül, hogy abba rácsszerűen, sűrűn egymás mellé kis lyukakat fúrunk. Kezdetben a lap nincs szupravezető állapotban, és egy

m

dipólmomentumú, a hálótól

a

távolságban lévő mágneses dipólus merőlegesen a háló felé mutat. Ekkor a hálót lehűtjük, és így szupravezetővé válik. Ezután a dipólust a felületre merőleges irányban elmozdítjuk úgy, hogy az új távolsága a hálótól

b

legyen.

Határozd meg a háló és a dipólus közt fellépő erőt! A lyukrács rácsállandója (a lyukak egymástól mért távolsága) sokkal kisebb, mint

a

és

b

, a lap lineáris mérete viszont sokkal nagyobb, mint

a

és

b

Megoldás. A megoldás kulcsa az, hogy észrevegyük: a mágneses fluxus ,,beszorul'' a szupravezető hálóba. Mindenekelőtt ezt a hatást gondoljuk meg. Miután a hálót szupravezető állapotúra hűtjük, a mágneses mező minden helyen ,,állandósul'', nem változhat meg, akárhogyan is mozgatjuk a mágneses dipólust. Mivel a mágneses mező jól meghatározott a háló mentén, a feladat igazából egy határfeltétel-probléma, amit általában tükörtöltésekkel szoktunk megoldani.
Nézzük meg, mit történik, ha a dipólust eltávolítjuk a hálótól nagyon messzire. El kell helyeznünk egy tükördipólust, ami pont ugyanazt a mágneses mezőt hozza létre a háló mentén, mint az eredeti mágnes. Ezt megoldhatjuk egy dipólussal, amely

a

távolságra van a háló mögött, és szintén

m

a dipólmomentuma. Most hozzuk vissza az eredeti dipólust

b

távolságra a hálótól. Ennek a mezejét viszont ki kell zárnunk a szupravezető hálóból, ezt egy

- m

momentumú, a háló mögött

b

távolságra lévő dipólussal tehetjük meg.
A továbbiakban a tükördipólusok által a dipólusra ható erőt kell meghatároznunk. Ezt például a mágneses és az elektromos dipólusok közötti analógia felhasználásával tehetjük meg. A mágneses dipólusokra egymáshoz nagyon közeli,

q_{m}

és

- q_{m}

nagyságú ,,mágneses töltésekként'' is gondolhatunk, amelyek egymástól

d

távolságra vannak, ahol

m = q_{m} d

.
Határozzuk meg a dipólus mágneses térerősségét a dipólus tengelye mentén, a dipólustól

x ≫ d

távolságban:

\begin{matrix} B = \frac{μ_{0}}{4 π} \frac{q_{m}}{x^{2}} + \frac{μ_{0}}{4 π} \frac{- q_{m}}{{(x + d)}^{2}} \approx \frac{μ_{0}}{4 π} \frac{q_{m}}{x^{2}} - \frac{μ_{0}}{4 π} \frac{q_{m}}{x^{2}} (1 - 2 \frac{d}{x}) = \frac{μ_{0}}{2 π} \frac{q_{m} d}{x^{3}} = \frac{μ_{0}}{2 π} \frac{m}{x^{3}} . \end{matrix}

Most vizsgáljuk meg az

x

helyen lévő dipólusra ható erő nagyságát egy inhomogén,

B (x)

helyfüggésű mágneses mezőben:

\begin{matrix} F = - q_{m} B (x) + q_{m} B (x + d), \end{matrix}

amit kifejezhetünk

B (x)

deriváltja segítségével is:

\begin{matrix} F \approx - q_{m} B (x) + q_{m} (B (x) + d \cdot \frac{d B}{d x} |_{x}) = q_{m} d (- \frac{3 μ_{0}}{2 π} \frac{m}{x^{4}}) = - \frac{3 μ_{0}}{2 π} \frac{m^{2}}{x^{4}} . \end{matrix}

A negatív előjel azt jelenti, hogy két párhuzamos dipólus vonzza egymást.
Visszatérve a feladathoz, a

b

távolságra lévő dipólust vonzza a

- a

távolságra lévő dipólus, de taszítja a

- b

távolságra lévő. Vagyis az eredő erő:

\begin{matrix} F = - \frac{3 μ_{0}}{2 π} \frac{m^{2}}{{(a + b)}^{4}} + \frac{3 μ_{0}}{2 π} \frac{m^{2}}{{(b + b)}^{4}} = \frac{3 μ_{0} m^{2}}{2 π} (\frac{1}{16 b^{4}} - \frac{1}{{(a + b)}^{4}}), \end{matrix}

ahol a negatív előjel azt jelenti, hogy a dipólus vonzást érez a háló felé.

Izgalmas megnézni azt az esetet, ha

b

és

a

közel egyenlőek, vagyis

b = a + δ

(

δ ≪ a

). Ebben az esetben

\begin{matrix} F = \frac{3 μ_{0} m^{2}}{2 π} (\frac{1}{16 {(a + δ)}^{4}} - \frac{1}{{(2 a + δ)}^{4}}), \end{matrix}

vagyis

\begin{matrix} F \approx \frac{3 μ_{0} m^{2}}{2 π} \frac{1}{16 a^{4}} ((1 - 4 \frac{δ}{a}) - (1 - 4 \frac{δ / 2}{a})), \end{matrix}

ami tovább egyszerűsödik:

\begin{matrix} F \approx - \frac{3 μ_{0} m^{2}}{16 π a^{5}} δ . \end{matrix}

A negatív előjel miatt ez az erő

δ > 0

esetén a háló felé mutat. A pozitív

δ

itt azt jelenti, hogy távolítjuk a dipólust a hálótól. Látható, hogy az

F

erő lineárisan változik a hely függvényében, tehát ha kicsit kimozdítjuk a dipólust az eredeti (egyensúlyi) helyzetéből, akkor ‐ egyéb erők hiányában ‐ harmonikus rezgőmozgást fog végezni.