Kezdőlap


Cím:	Mohó algoritmusok 3. ‐ az I/S. 12. feladat megoldása
Füzet:	2017/május, 285 - 292. oldal	PDF \| MathML
Hivatkozás(ok):	Feladatok: 2016/november: I/S.12

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A mohó stratégia alkalmazása kapcsán foglalkoztunk a 2016 októberében megjelent számban a címletezés problémájával: fizessünk ki adott pénzösszeget a rendelkezésre álló papírpénzek és érmék (vagyis adott címletek) segítségével úgy, hogy a lehető legkevesebb számú pénzdarabot használjuk föl. A ma szokásos címletek mellett a feladat megoldható mohó módszerrel. Az eljárás a következő: megnézzük, hogy melyik az a címlet, amely még nem nagyobb a kifizetendő összegnél, és abból a lehető legtöbbet fölhasználva fizetünk; ezután ugyanezt tesszük a kifizetés után fennmaradó összeggel, és így tovább. Ha van 1 értékű a címletek között, akkor minden pénzösszeg kifizethető, egyébként nem feltétlenül.
A hivatkozott cikkben szerepel a következő állítás: ha $c_{1}, c_{2}, ..., c_{n}$ pozitív címletekre teljesül, hogy $2 c_{i} \leq c_{i + 1}$ ( $1 \leq i < n$ ), akkor a címletezésre adott mohó megoldás optimális, tehát a lehető legkevesebb számú címletet használja föl a kifizetéshez. Elnézést kérek az olvasóktól, sajnos egy ,,közismert'' tévedést adtam tovább, az állítás nem igaz! Például az 1, 4, 9 címletek mellett a 12 kifizetéséhez a mohó módszer a $12 = 9 + 1 + 1 + 1$ címletezést adja, pedig a $12 = 4 + 4 + 4$ kevesebb számú pénzt használ föl. A téves állítás azért olyan hihető, mert ha $2 c_{i} = c_{i + 1}$ $(1 \leq i < n)$ , akkor a feladatra optimális megoldást kapunk a fent leírt mohó stratégiával.

Fontos tehát, hogy egy mohó stratégia alkalmazása előtt igazoljuk, hogy a módszerrel talált megoldás optimális. A mohó megoldás menete a következő lépésekből áll. Először a teljes feladatot két részfeladatra bontja. Az egyik részfeladatot optimálisan megoldja a részfeladatból kiolvasható információk alapján. Ezután a másik részfeladatot megint két részre bontja, és azok közül megoldja az egyiket úgy, hogy optimális megoldást ad, és így tovább. Amennyiben a részfeladatokra adott optimális megoldások a teljes feladat optimális megoldását adják, akkor a mohó stratégiával kapott megoldás optimális megoldása az eredeti feladatnak.
Nézzük a címletezés feladatra adott mohó megoldást (természetesen abban az előbb említett esetben, amikor az egymást követő címletek pontosan egymás kétszeresei). Vegyük észre, hogy ilyen speciális címletek mellett minden olyan megoldás, amely a nem legnagyobb címletből egynél több darabbal fizet nem optimális, hiszen két ilyen címlet helyettesíthető egy nagyobb címlettel. Ugyanakkor az is igaz, hogy egy adott címlet értéke 1-gyel nagyobb az összes, nála kisebb címletek mindegyikének egyszeri fölhasználásával kifizetett összegnél (2-es számrendszer). A bizonyítás lépései ezek alapján:
1. Hasonlítsunk össze egy mohó stratégiával kapott eredményt, és egy másik módszerrel kapott optimális megoldást. A mohó megoldás a címletek közül elsőként a legnagyobb olyan címletet választja (legyen ez

c_{m}

), amely még nem haladja meg a kifizetendő

p

összeget.

2. a

. Ha az optimális megoldás is ezzel a címlettel fizet, akkor a mohó módszer a legnagyobb címletben megegyezik a másik, optimális megoldással.

2. b

. Ha az optimális megoldás a mohó megoldásnál nagyobb címlettel fizet, akkor több mint

p

összeget fizet ki, tehát a megoldás nem helyes.

2. c

. Ha az optimális megoldás a mohó megoldásnál kisebb címlettel fizet, akkor legföljebb

c_{m} - 1

pénzösszeget tud kifizetni az összes

c_{m}

-nél kisebb címlet egyszeri fölhasználásával. Azonban

p \geq c_{m}

, tehát ez a megoldás nem lehet optimális.
Mivel a

2. b

. és

2. c

. pontokban ellentmondásra jutottunk, ezért csak a

2. a

. pont lehetséges. A legnagyobb,

p

-t nem meghaladó címlet mohó választása tehát jó döntés volt. Amennyiben még maradt kifizetendő pénz, úgy folytassuk a

p - c_{m}

összeg kifizetésével az 1. pontra visszatérve. Ismét csak az lehetséges, hogy azonos a következő címlet kiválasztása. Ha még ezután a kifizetés után is maradt kifizetendő összeg, akkor ismét térjünk vissza az 1. pontra. Minden ilyen esetben a pénzösszeg csökken, ezért a gondolatmenet véges lépésben befejeződik. Tehát a mohó és az optimális megoldás megegyezik. Ezzel igazoltuk, hogy a feladatra adott mohó megoldás is optimális.

Kérdések és feladatok
1. feladat: Optimális megoldást ad-e a mohó módszer a címletezés problémájára akkor, ha az egymást követő címletek egymás

a

-szorosai (

a \geq 2

és

c \geq 1

egészek), tehát a címletek

c

a c

...

a^{n - 1} c

? Ha igen, akkor igazoljuk a mohó stratégia alkalmazásának helyességét, ha nem, akkor adjunk ellenpéldát.

Foglalkozzunk a továbbiakban a 2016. novemberében kitűzött I/S. 12. feladattal. A feladat pontos szövege megtalálható weboldalunkon, itt most csak a probléma rövidebb leírását adjuk. Fedjünk le

1 \times 1

1 \times 2

2 \times 2

2 \times 4

...

2^{N} \times 2^{N}

2^{N} \times 2^{N + 1}

méretű négyzetekkel és téglalapokkal (csempékkel) egy

a \times b

méretű téglalapot (

a

b

és

N

pozitív egészek).
A feladat egy címletezés probléma kiterjesztése két dimenzióba. A feladatra sok szép és egészen frappáns megoldás érkezett, melyek ‐ egy kivétellel ‐ lényegében a mohó stratégiát alkalmazták. A nem mohó megoldás dinamikus programozással történt. A versenyzők közül egyedül Nagy Nándor tért ki arra a dokumentációjában, hogy a mohó módszer alkalmazhatóságát igazolni kell. Természetesen a helyes és érthető leírást tartalmazó megoldások a mohó módszer helyességének bizonyítása nélkül is teljes pontszámot értek. Mégis ‐ a fenti tapasztalatok alapján ‐ érdemes meggondolni, hogy tényleg jó-e a mohó megoldás.

Ahogyan a címletezés feladatnál tettük, vizsgáljuk meg itt is a címleteket, azaz a csempéket. Jelöljük a legkisebb, azaz

1 \times 1

-es területét

t_{0}

-lal, a

2 \times 1

-es területét

t_{1}

-gyel, a méret szerinti sorrendben

n

-edik területét

t_{n}

-nel. A terület szerint növekvő sorrendbe állított csempékre igaz, hogy ‐ a legkisebb kivételével ‐ mindegyik csempe területe az előző területének kétszerese, ezért

t_{n} = 2^{n}

.
Vegyük észre, hogy a legkisebb csempén kívül bármelyik csempe helyettesíthető két feleakkora területű másik csempével. Például egy

8 \times 4

-es csempe helyettesíthető két

4 \times 4

-es csempével. De ez a két csempe is helyettesíthető két fele akkora területűvel. Tehát a

8 \times 4

-es csempe akár egy

4 \times 4

-es, három

2 \times 2

-es és két

2 \times 1

-es csempére is cserélhető (lásd az 1. ábrát az első belső borítón). Ez az érdekes tulajdonság abból ered, hogy ha vesszük a csempék egy csoportját, amelyek összes területe egyenlő egy nagyobb csempe területével, akkor azokból mindig fölépíthető a nagyobb csempe. Például az előbbi

8 \cdot 4 = 32

terület esetén legyen a csempék területe

32 = 5 \cdot 4 + 3 \cdot 2 + 6 \cdot 1

. Ha a hat darab 1 területűt összerakjuk, akkor éppen három 2 területűt kapunk; ha a most összesen hat darab 2 területűt összerakjuk, akkor három 4 területűt kapunk; az így nyert nyolc darab 4 területű pedig pontosan lefedi a

8 \times 4

-es csempét (lásd a 2. ábrát a borítón). Természetesen fogalmazzuk meg általánosan és igazoljuk észrevételünket:

1. ábra:

8 \times 4

-es csempe helyettesítései kisebb területű csempékkel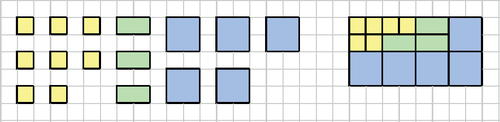

2. ábra: egy

8 \times 4

-es csempe összeállítása összesen 32 területű csempékből

1. állítás: Ha adott a csempék egy tetszőleges csoportja, melyek területének összege egyenlő egy nagyobb csempe területével, akkor a csoportban lévő csempékből kirakható a nagyobb csempe.
Bizonyítás: Az állítás triviális abban az esetben, ha a csempék csoportja egy elemből áll. Ha a csoport több csempét tartalmaz, akkor legyen a nagyobb csempe

2^{n}

területű, és jelöljük a csoportban lévő

t_{i}

területű csempék darabszámát

c_{i}

-vel (

0 \leq i < n

). Bizonyos

c_{i}

értékek lehetnek nullák. A területek egyenlősége szerint

\sum_{i = 0}^{n - 1} c_{i} \cdot 2^{i} = 2^{n}

.
Ha a legkisebbekből párokat alkotunk, akkor a párok a nagyság szerint következő méretű csempéket adják. Először lássuk be, hogy a legkisebb méretű csempéből páros számú van. Legyen a legkisebb nem nulla darabszámú csempe indexe

k

. Osszuk a területek egyenlőségét jelentő egyenletet a legkisebb csempe területével, azaz

2^{k}

-nal, majd nézzük a két oldal paritását. Mivel a

k

-adik csempe a legkisebb területű, ezért a jobb oldal, és a bal oldalon a szorzatösszeg minden

k

-nál nagyobb indexű tagja páros, ezért

c_{k}

is csak páros lehet.
A legkisebbek párosítása után most a csempék egy újabb csoportjával van dolgunk. Ezek területének összege nem változott, ezért az előző gondolatmenet alapján ismét csak páros darabszámú van a legkisebb csempéből. Vagyis folytathatjuk a párosításokat egészen addig, amíg a

2^{n}

területű csempét össze nem állítjuk. Ezzel állításunk igazoltuk.
Ebből következik, hogy ha egy csempe alakú területet szeretnénk lefedni, akkor az egy azzal egyenlő területű csempével, vagy több, összesen azzal egyenlő területű csempével együttesen lefedhető.

Egy olyan, mohó stratégiára épülő megoldást szeretnénk adni, amely a lefedés egymást követő lépéseiben mindig a lehető legnagyobb méretű csempét használja föl. Bontsuk fel ennek megfelelően az

a \times b

oldalú téglalapot az oldalakkal párhuzamos egyenesekkel a következők szerint.
Vegyük az egyik oldalhosszúság, pl.

a

kettes számrendszerbeli alakját, és válasszuk ki abban a nem nulla helyiértékeket. Jelöljünk ki a téglalap jobb alsó sarkától indulva ilyen hosszúságú szakaszokat egymás mellett. Ezután húzzunk a szakaszok végpontjain át az

a

hosszú oldalra merőlegesen egyeneseket. Végezzük el ugyanezt a

b

oldallal is, szintén a jobb alsó sarokból indulva. Például egy

15 \times 9

-es téglalap esetén az osztóvonalak

15 = 8 + 4 + 2 + 1

miatt 1, 2, 4 és 8 hosszú szakaszokat hoznak létre a

15

hosszú oldalon, valamint

9 = 8 + 1

alapján 8 és 1 hosszú szakaszokat a másik oldalon (lásd a 3. ábrát a borítón). Így az osztásrészek között olyan téglalapok keletkeznek, melyek mindkét oldala 2-hatvány, ami azt jelenti, hogy az oda még elférő, legnagyobb méretű csempe egy vagy több darabjával lefedhetők. Ha pl. egy osztásrész mérete

2^{p} \times 2^{q} (p \leq q)

, akkor az oda elférő legnagyobb csempe nem hosszabb oldala

2^{p}

. Ha

p = q

, akkor a megfelelő csempe négyzet alakú, és egy darab lefedi az osztásrészt. Ha

p < q

, akkor a csempe és az osztásrész területe alapján a

2^{p} \times 2^{p + 1}

csempéből

2^{p + q} / 2^{2 p + 1} = 2^{q - p - 1}

darab fedi le az osztásrészt. Amennyiben a feladat leírása szerint meghatározott legnagyobb csempénél nagyobb az osztásrész rövidebb oldala, azaz

p > N

, akkor a

2^{N} \times 2^{N + 1}

méretű csempékkel borítjuk a területet, összesen

2^{p + q} / 2^{2 N + 1}

darabot fölhasználva. Mivel minden osztásrész csempe méretű, ezért az 1. állítás szerint a lefedés mindig végrehajtható (lásd a 4. ábrát a borítón).

3. ábra:

15 \times 9

-es téglalap felosztása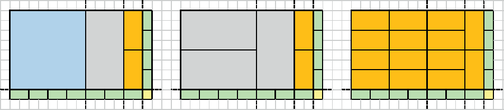

4. ábra:

15 \times 9

-es téglalap mohó lefedése

N = 3

N = 2

és

N = 1

esetén

A bemutatott mohó stratégia minden osztásrészben optimális lefedést jelent, tehát a legkevesebb csempét használja. Ez sajnos egyelőre csak az osztásrészekre igaz, azt nem tudhatjuk, hogy a teljes

a \times b

téglalap lefedése is optimálisan történt-e. De ha sikerül bebizonyítani, hogy bármilyen lefedés csempéi átrendezhetők úgy, hogy a fenti osztásrészekbe kerüljenek, vagyis az osztóvonalak egy csempét se vágjanak ketté, akkor a mohó stratégia valóban optimális. Az átrendezés ugyanis azt jelenti, hogy bármely megoldás a mohó stratégia szerinti felosztásokat, mint részproblémákat is megoldja. Mivel a felosztásokkal keletkező részproblémákban a mohó megoldás optimális, ezért bármilyen más megoldás is csak úgy lehet optimális, ha a részproblémák megoldásakor az. Ugyanakkor nem lehet a mohó megoldásnál kisebb elemszámú megoldást adni, mivel annak legalább az egyik osztásrészt a mohó megoldásnál kevesebb számú csempével kell lefednie, ami nem lehetséges.

Annak igazolásához, hogy tetszőleges lefedés átrendezhető a 2-hatvány szerinti osztásrészekbe, meg kell mutatnunk, hogy a legkisebb osztásrészek lefedéséhez is van elegendő számú, megfelelően kis méretű csempe. Ha például egy

11 \times 7

-es téglalapot tekintünk, akkor az átrendezéshez bármilyen lefedésnek tartalmaznia kell legalább egy

1 \times 1

-es, és még legalább összesen

11 + 7 - 1

területű, 1 szélességű csempét. Az

1 \times 1

-es csempéből nyilván páratlan számú van a lefedésben, hiszen a nála nagyobb, páros oldalszámú csempék területének összege páros, míg a téglalap területe páratlan. Az észrevétel alapján a párosság vizsgálatát terjesszük ki két dimenzióba: tegyünk egy négyzethálót a lefedendő téglalapra, és jelöljük meg betűkkel a bal felső saroktól kiindulva a

2 \times 2

-es négyzetek részeit az óramutató járásával egyező irányban az A, B, C és D betűkkel (lásd az 5. ábrát a borítón). Minden olyan csempe, amely

2 \times 2

-es, vagy nagyobb méretű, azonos számú A, B, C és D betűt fed le, bárhol is helyezzük el a téglalapon. Általánosan egy

a \times b

téglalapot vizsgálva a következő esetek fordulhatnak elő.

5. ábra:

11 \times 7

-es téglalap négyzeteinek jelölése A, B, C, D betűkkel egy tetszőleges lefedés mellett, valamint az 1 széles csempék áthelyezése és egyesítése, a nagyobb csempék tologatása

0.

Ha a téglalap egyik oldala, pl.

b

egy egység hosszú, akkor nyilván 1 széles csempék vannak rajta. Rendezzük a

2 \times 1

-es csempéket balra, az

1 \times 1

-eseket jobbra. A lefedés átrendezését befejeztük, a 2-hatványok szerint kialakított osztóvonalak nem vágnak ketté egy csempét sem.

1.

Ha a téglalap mindkét oldala páratlan (de 1-nél nagyobb), akkor a teljes téglalap

a b

területe páratlan szám. Mivel a csempék közül csak az

1 \times 1

-es páratlan területű, ezért lennie kell minden lefedésben páratlan számú, tehát legalább egy ilyen csempének. A téglalap négyzeteinek jelölése alapján pedig:

i)

a téglalap bal felső négyzetét is tartalmazó

(a - 1) \times (b - 1)

részén azonos számú A, B, C és D jelű négyzet van;

i i)

a jobb alsó sarokban egy A jelű négyzet van;

i i i)

a jobb alsó sarok fölött, az utolsó oszlopban A és D jelű négyzetekből egyaránt

(b - 1) / 2

darab van;

i v)

a jobb alsó sarok mellett, az utolsó sorban A és B jelű négyzetekből egyaránt

(a - 1) / 2

darab van.
Ezek alapján A, B és D jelű négyzetből összesen

(b - 1) + (a - 1) + 1

-gyel több van, mint C jelű négyzetből. Mivel a legalább 2 széles csempék azonos számú A, B, C és D jelű négyzetet fednek, ezért a különbségként előbb kapott

a + b - 1

számú négyzetet legföljebb egy széles csempék borítják.

2.

Ha a lefedendő terület egyik oldalhossza, pl.

a

páros, a másik oldalhossza,

b

páratlan (de 1-nél nagyobb), akkor az

1.

ponttal azonos módon igazolható, hogy a lefedésben legalább

a

számú négyzetet 1 széles csempék fednek.

3.

Ha mindkét oldalhossz páros, akkor lehetséges, hogy nincs 1 széles csempe a lefedésben, de nem is szükséges őket fölhasználnunk, mert nincs páratlan utolsó sor és oszlop.
Vegyük le az összes 1 széles csempét a lefedésből. Az

1.

esetben rakjunk egy

1 \times 1

-es csempét a jobb alsó sarokba, valamint az utolsó sor és oszlop további ‐ páros hosszú ‐ részére helyezzünk 1 széles csempéket. A

2.

esetben tegyünk a páros hosszú utolsó sorra vagy oszlopra 1 széles csempéket.
Ezekután a téglalap lefedése ‐ kivéve azt az esetet, amikor nem vettünk le 1 széles csempéket ‐ nem megfelelő, hiszen elképzelhető, hogy az utolsó oszlopban és/vagy sorban lévő négyzeteket két csempe is fedi, illetve a téglalap lefedése az 1 széles csempék levétele miatt még hiányos. Ezeket a problémákat úgy szüntetjük meg, hogy a téglalapon lévő, legalább 2 széles csempék mindegyikét olyan helyzetbe toljuk, hogy a bal felső sarkuk egy A jelű négyzetre essen, majd a még lefedetlen területeket a levett csempékkel borítjuk.
Induljunk el a bal felső saroktól soronként lefelé, a sorokon belül balról jobbra haladva, és keressük meg az első olyan 2 széles csempét, amelynek bal felső sarka C vagy D jelű négyzetre esik. Ha nincs ilyen, akkor fölfelé egy csempét sem mozgatunk. Ha van, akkor az első ilyen csempe fölött biztosan van sor, amelynek a csempe fölötti A és B jelű négyzetei nem fedettek, tehát egy sorral fölfelé tolható, így A vagy B jelű négyzetre kerül a bal felső sarka. Ha ezt megtettük, akkor folytatjuk a keresést tovább a soron belül, majd az alatta lévő sorokban. Az így talált első csempe, amelynek bal felső sarka C vagy D jelű négyzetre esik, szintén eltolható egy sorral följebb. Ha már nincs több, akkor minden legalább 2 széles csempe bal felső sarka A vagy B jelű négyzetre esik. Így biztosan megszüntettük a páratlan utolsó sorban a kettős lefedést.
Hasonló módon végighaladunk a bal felső saroktól indulva, oszloponként, az oszlopokon belül fölülről lefelé, és megkeressük az első olyan, legalább 2 széles csempét, amelynek bal felső sarka B jelű négyzetre esik. Ettől a csempétől balra van oszlop, amelynek a csempe melletti A és D jelű négyzetei nem fedettek, tehát a csempe eggyel balra tolható. Folytatva a keresést a következőként megtalált első csempe szintén eltolható úgy, hogy a bal felső sarka A jelű négyzetre kerüljön. Ha már minden legalább 2 széles csempe bal felső sarka A jelű négyzetre esik, akkor megszüntettük a páratlan utolsó oszlopban a kettős lefedést.
Ezután minden legalább 2 széles csempe bal felső sarka A jelű, jobb alsó sarka C jelű négyzetre esik, ezért a levett csempék miatt fedetlenül maradt részek legalább 2 szélesek és 2 magasak. Ezeket a területeket bontsuk

2 \times 2

-es részekre, és a levett, de eddig még nem fölhasznált 1 széles csempékből összevonással készítsünk ilyen méretű csempéket, majd fedjük le őket. Mivel a

2 \times 2

csempeméret, ezért az 1. állítás miatt ez megtehető. A csempék összterülete nem változott, így minden levett csempét biztosan visszahelyezünk a téglalapra. Nincs kettős fedés, így a téglalap lefedése az eredeti csempékkel, de más elrendezésben most is megfelelő (lásd az 5. ábrát a borítón).

Az előző lépések alapján sikerül bármilyen lefedést úgy átrendezni, hogy a páratlan oldalak utolsó sora és/vagy oszlopa 1 széles csempékkel van lefedve. Ha az összevont csempéket egy-egy

2 \times 2

-es csempének tekintjük, akkor a téglalap páros oldalhosszakkal határolt része csak

2 \times 2

-es vagy nagyobb méretű csempét tartalmaz. Végezzünk ezen a téglalaprészen pl. a bal felső sarokból

1 / 2

arányú középpontos kicsinyítést. Így egy feleakkora téglalap lefedését kapjuk feleakkora ‐ bizonyos helyeken összevont ‐ csempékkel. Térjünk vissza az így kapott téglalappal és lefedésével a 0‐3. megfelelő esetéhez, és végezzük el újra az előbbieket. Minden olyan esetben, amikor nem a 0. ponthoz jutunk, a téglalap mérete csökken, így az eljárás véges ismétlés után befejeződik. Amikor a 0. ponthoz értünk, akkor a kicsinyítések sorozata után keletkező 1 széles vagy magas téglalap lefedése olyan, hogy egyetlen osztóvonal sem vág ketté csempét (lásd a 6. ábrát a borítón).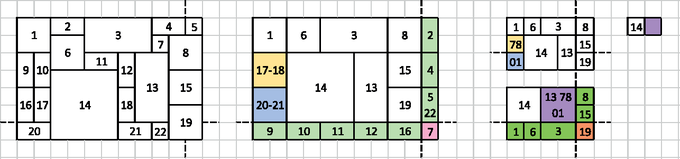

6. ábra:

11 \times 7

-es téglalap egy lefedésének átalakítása: a páratlan sorok és/vagy oszlopok leválasztása, az 1 széles csempékből

2 \times 2

-esek összeállítása, a csempék tologatása, majd kicsinyítés ‐ ,,S megint előlről

...

Ezután nincs más teendőnk, mint az előbbi eljárás fordítottját elvégezve visszaállítani az eredeti méretű, teljes téglalapot. Először az előbbi eljárás végén kapott téglalapot a kétszeresére nagyítjuk, az összevont csempéket szétbontjuk, és az utolsó sorokat és/vagy oszlopokat a helyükre illesztjük. Mivel a visszaillesztés egy osztóvonal mentén történik, valamint nagyításkor az osztóvonalak távolsága a csempék méretével együtt nő, ezért egy-egy ilyen műveletsor elvégzése után is teljesül, hogy az osztóvonalak nem vágnak el csempét. Ha még nem jutottunk az

a \times b

téglalaphoz, akkor ismét nagyítunk, szétbontunk, visszaillesztjük a páratlan oszlopokat stb. Az így kapott eredeti téglalapon a kiinduláskor ott lévő csempék vannak, de úgy helyezkednek el, hogy a 2-hatvány hosszú osztásrészek osztóvonalai által kialakított téglalapok mindegyike külön-külön van lefedve csempékkel (lásd a 7. ábrát a borítón). Tehát bármely lefedés átrendezhető a mohó megoldáshoz kialakított, csempe méretű téglalapok lefedésével, vagyis valójában bármely megoldás a mohó megoldás részproblémáit is megoldja.

7. ábra: a 6. ábrán látható lefedés átalakítása a mohó megoldás felosztásának megfelelően

Sikerült igazolni, hogy a fent leírt mohó stratégia optimális megoldását adja a feladatnak. Nézzük a versenyzők által beküldött megoldásokat, melyek közül elsőként Janzer Orsolya Lili munkáját mutatjuk be:

Függvény IS12mo_1(a, b, N) : Egész
    db := 0
    Ciklus k := 0-tól N-ig
        Ha (a MOD 2 = 1) és (b MOD 2 = 0) akkor db := db + b DIV 2
        Ha (a MOD 2 = 0) és (b MOD 2 = 1) akkor db := db + a DIV 2
        Ha (a MOD 2 = 1) és (b MOD 2 = 1) akkor db := db + a DIV 2 + b DIV 2 + 1
        a := a DIV 2
        b := b DIV 2
    Ciklus vége
    db := db + a*b*2
    IS12mo_1 := db
Függvény IS12mo_1 vége

Az algoritmus

k

értékével végighalad a feladatban megadott legnagyobb

N

2-hatvány kitevőig. Első menetben megvizsgálja az oldalhossszak 2-es maradékát, vagyis az utolsó oszlopot és sort, és kiszámítja, hogy mennyi elem szükséges a lefedésükhöz. Ezzel megold egy-egy részproblémát, vagyis a páratlan utolsó sorok és/vagy oszlopok eseteit. Ha mindkét érték páratlan, akkor még a jobb alsó sarkot is lefedi. Ezután egész osztással megfelezi

a

és

b

értékét, tehát elhagyja a páratlan utolsó sorokat és oszlopokat, valamint felére csökkenti mindkét irányból a lefedendő alakzatot. Így a ciklus következő lefutásakor a következő 2-hatvánnyal teszi pontosan ugyanazt, mint most a 2-vel. A ciklus utolsó végrehajtása után a

2^{N}

-nél nagyobb részek lefedéséhez szükséges csempéket adja hozzá az eddigiekhez. Vegyük észre a fenti bizonyítás, és az algoritmus közötti párhuzamokat.
A másik megoldás, amit közreadunk Gáspár Attila munkája, amely lényegében egy rekurzív függvény. Az algoritmusban szereplő & jel a bitenkénti és műveletet jelenti, tehát (a & 1) kifejezés értéke

a

-nak kettővel vett osztási maradéka.

Függvény IS12mo_2(a, b, N) : Egész
    Ha N=0 akkor IS12mo_2 := (a*b+1) DIV 2
    különben
        db := is12mo_2(a DIV 2, b DIV 2, N-1)
        db := db + (a & 1) * (b DIV 2) + (b & 1) * (a DIV 2) + (a & b & 1)
        IS12mo_2 := db
    Elágazás vége
Függvény IS12mo_2 vége

Szintén jól megfigyelhető a rekurzív algoritmusban a bizonyított mohó stratégia alkalmazása.
A harmadik megoldás Nagy Nándor munkája, amely szintén egy rekurzív függvény. Az előzőek után nem szorul magyarázatra. Azonnal látható az előbbi megoldással való hasonlóság, de tanulságos meggondolni a közöttük meglévő különbségeket is.

Függvény IS12mo_3(a, b, N) : Egész
    Ha a=0 vagy b=0 akkor IS12mo_3 := 0
    különben
        h :=

2^{N - 1}

        au := a DIV h :      am := a MOD h
        bu := b DIV h :      bm := b MOD h
        szum := (au*bu) DIV 2 + (au*bu) MOD 2
        szum := szum + IS12mo_3(am, bu*h, N-1)
        szum := szum + IS12mo_3(bm, au*h, N-1)
        szum := szum + IS12mo_3(am, bm, N-1)
        IS12mo_3 := szum
    Elágazás vége
Függvény IS12mo_3 vége

Kérdések és feladatok
2. feladat: Gondoljuk meg, hogy megoldható-e ‐ a fentihez hasonló ‐ mohó módszerrel a téglalap lefedős feladat olyan változata, amelynél a csempék mindegyike

2^{u} \times 2^{v}

alakú (

0 \leq u, v \leq N

). Ha igen, akkor igazoljuk a mohó módszer alkalmazhatóságát. Ha nem, akkor adjunk ellenpéldát, amelynél a mohó megoldás nem optimális.
3. feladat: Vajon működik-e a fent leírt mohó módszer, ha az eredeti feladatban nem a 2-hatványokat választjuk, hanem a csempék mérete valamely

c

, egytől különböző pozitív egész hatványai, vagyis a csempék

c^{k} \times c^{k}

vagy

c^{k} \times c^{k + 1}

alakúak (

0 \leq k \leq N

)? Gondoljuk meg, hogy a fenti bizonyítás ‐ megfelelő változtatással ‐ helyes marad-e! Ha nem, akkor adjunk ellenpéldát, amelynél a mohó megoldás nem optimális.
4. feladat: Amennyiben a mohó módszer alkalmazható a kitűzött példák megoldására, úgy készítsük el az algoritmusokat.