Cím:	Megoldásvázlatok a 2017/4. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Vancsó Ödön ,  Varga Péter
Füzet:	2017/május, 258 - 266. oldal	PDF  |  MathML
Hivatkozás(ok):	2017/április: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg a valós számok halmazán az alábbi egyenleteket: $a)$ $\begin{array}{c}{\displaystyle \sqrt[]{5^{x-1}}=\sqrt[3]{0\mathrm{,}{2}^{4x-20\mathrm{,}5}}\mathrm{,}}\end{array}$  (5 pont) $b)$ $\begin{array}{c}{\displaystyle \text{cos}\left(x-\frac{5\pi }{6}\right)=\text{sin}x\mathrm{.}}\end{array}$  (6 pont)   Megoldás. $a)$ A hatványozás azonosságainak felhasználásával: $5^{\frac{x-1}{2}}=5^{\frac{20\mathrm{,}5-4x}{3}}$. Az 5-ös alapú exponenciális függvény szigorú monotonitása vagy kölcsönös egyértelműsége miatt $\frac{x-1}{2}=\frac{20\mathrm{,}5-4x}{3}$, melynek megoldása $x=4$. Ellenőrzés behelyettesítéssel vagy az értelmezési tartomány $\left(x\in \text{R}\right)$ feltüntetése mellett az ekvivalens átalakításokra hivatkozással. $b)$ I. megoldás. A $\text{sin}x=\text{cos}\left(x-\frac{\pi }{2}\right)$ összefüggést felhasználva $\begin{array}{c}{\displaystyle \text{cos}\left(x-\frac{5\pi }{6}\right)=\text{cos}\left(x-\frac{\pi }{2}\right)\mathrm{.}}\end{array}$ Tudjuk, hogy $\text{cos}\alpha =\text{cos}\beta \iff \alpha =\pm \beta +2k\pi$, ahol $k\in \text{Z}$. Ha $\alpha =\beta +2k\pi$, akkor $x-\frac{5\pi }{6}=x-\frac{\pi }{2}+2k\pi$ $\left(k\in \text{Z}\right)$, melynek nincs megoldása. Ha $\alpha =-\beta +2k\pi$, akkor $x-\frac{5\pi }{6}=-x+\frac{\pi }{2}+2k\pi$, ahonnan $x=\frac{2\pi }{3}+k\pi$ $\left(k\in \text{Z}\right)$. Ellenőrzés behelyettesítéssel, vagy az értelmezési tartomány $\left(x\in \text{R}\right)$ felírása mellett az ekvivalens átalakításokra hivatkozással. II. megoldás. Az addíciós tételt felhasználva $\begin{array}{c}{\displaystyle \text{cos}\left(x-\frac{5\pi }{6}\right)=\text{cos}x\cdot \text{cos}\frac{5\pi }{6}+\text{sin}x\cdot \text{sin}\frac{5\pi }{6}\mathrm{,}}\end{array}$ így az egyenlet $\begin{array}{c}{\displaystyle \text{cos}x\cdot \text{cos}\frac{5\pi }{6}+\text{sin}x\cdot \text{sin}\frac{5\pi }{6}=\text{sin}x}\end{array}$ alakba írható, melyet rendezve a $\begin{array}{c}{\displaystyle -\frac{\sqrt[]{3}}{2}\cdot \text{cos}x=\frac{1}{2}\cdot \text{sin}x}\end{array}$ egyenlethez jutunk. Mivel nincs olyan $x$, amelyre $\text{sin}x$ és $\text{cos}x$ egyszerre 0 lenne, ezért az egyenletnek nem lehet olyan gyöke, amelyre $\text{cos}x=0$, így az egyenlet mindkét oldalát $\frac{1}{2}\text{cos}x$-szel osztva $\text{tg}x=-\sqrt[]{3}$, ahonnan $x=\frac{2\pi }{3}+k\pi$ $\left(k\in \text{Z}\right)$. Ellenőrzés behelyettesítéssel vagy az értelmezési tartomány $\left(x\in \text{R}\right)$ felírása mellett az ekvivalens átalakításokra hivatkozással.   2. Egy bank 500 000 Ft kedvezményes kölcsönösszeget kínál fix 16 181 Ft-os heti törlesztő részlettel, $42$ hetes futamidőre. A szerződési feltételek értelmében az aktuális törlesztő részletet az ügyfél minden héten péntekig köteles átutalni a bank számlájára. Tudjuk, hogy az ügyfél által hetente elutalt összegeket a bank 0,5%-os azonnali kamatos kamatra tudja újra befektetni. (A kamatot a befizetéskor azonnal jóváírják.) $a)$ A felvett kölcsönösszeg hány százalékát fizeti vissza az ügyfél a banknak?  (3 pont) $b)$ Mekkora tényleges nyereséget ér el a bank ezzel a hitellel egy-egy ügyfélen?  (6 pont) A televízióban az egyik csatornán átlagosan minden negyedik hirdetés valamilyen hitelt reklámoz. Egy néző egy $12$ reklámból álló reklámblokkban $4$ hirdetést véletlenszerűen megnéz. $c)$ Mekkora annak a valószínűsége, hogy a megnézett négy reklám közül legalább kettő hitelt reklámoz?  (5 pont)   Megoldás. $a)$ Az ügyfél által a 42 hét alatt visszafizetett összeg $42\cdot 16181=679602$ Ft, mely a felvett kölcsönösszeg $\frac{679602}{500000}\cdot 100=135\mathrm{,}9204\approx 136\%$-a. $b)$ Az első törlesztést követően a bank pénze: $\begin{array}{c}{\displaystyle T_1=16181\cdot \left(1+\frac{0\mathrm{,}5}{100}\right)=16181\cdot 1\mathrm{,}005\text{Ft, }}\end{array}$ a második törlesztést követően: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_2}& {\displaystyle =\left(16181\cdot 1\mathrm{,}005+16181\right)\cdot 1\mathrm{,}005=16181\cdot 1\mathrm{,}{005}^2+16181\cdot 1\mathrm{,}005\text{Ft,}}\hfill \\ \hfill {\displaystyle }& {\displaystyle ⋮}\hfill \end{array}}$ míg a 42. törlesztést követően: $\begin{array}{c}{\displaystyle T_{42}=16181\cdot 1\mathrm{,}{005}^{42}+16181\cdot 1\mathrm{,}{005}^{41}+\text{...}+16181\cdot 1\mathrm{,}005\text{Ft. }}\end{array}$ A 42. heti törlesztést követően kapott összeget így is írhatjuk: $\begin{array}{c}{\displaystyle T_{42}=16181\cdot \left(1\mathrm{,}{005}^{42}+1\mathrm{,}{005}^{41}+\text{...}+1\mathrm{,}005\right)\mathrm{.}}\end{array}$ A zárójelben egy mértani sorozat első 42 tagjának összege szerepel, melynek első tagja $a_1=1\mathrm{,}005$, hányadosa $q=1\mathrm{,}005$. Ezt az összeget $S_{42}$-vel jelölve: $\begin{array}{c}{\displaystyle S_{42}=1\mathrm{,}005\cdot \frac{1\mathrm{,}{005}^{42}-1}{1\mathrm{,}005-1}\approx 46\mathrm{,}84.}\end{array}$ Tehát a bank tényleges nyeresége $16181\cdot S_{42}-500000\approx 258000$ Ft. $c)$ I. megoldás. Annak a valószínűsége, hogy egy reklám hitelt reklámoz 0,25. Annak a valószínűsége, hogy a megnézett négy reklám közül egyik sem hirdet hitelt: $\left(\genfrac{}{}{0ex}{}{4}{0}\right)\cdot 0\mathrm{,}{25}^0\cdot 0\mathrm{,}{75}^4\left(\approx 0\mathrm{,}3164\right)$. Annak a valószínűsége, hogy a megnézett négy reklám közül pontosan egy reklám hirdet hitelt: $\left(\genfrac{}{}{0ex}{}{4}{1}\right)\cdot 0\mathrm{,}{25}^1\cdot 0\mathrm{,}{75}^3\left(\approx 0\mathrm{,}4219\right)$. Így a kérdéses valószínűség: $p=1-0\mathrm{,}{75}^4-4\cdot 0\mathrm{,}25\cdot 0\mathrm{,}{75}^3\approx 0\mathrm{,}2617$. II. megoldás. Annak a valószínűsége, hogy egy reklám hitelt reklámoz 0,25. Annak a valószínűsége, hogy a megnézett négy reklám közül pontosan kettő reklámoz hitelt: $\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 0\mathrm{,}{25}^2\cdot 0\mathrm{,}{75}^2\left(\approx 0\mathrm{,}2109\right)$. Annak a valószínűsége, hogy a megnézett négy reklám közül pontosan három reklámoz hitelt: $\left(\genfrac{}{}{0ex}{}{4}{3}\right)\cdot 0\mathrm{,}{25}^3\cdot 0\mathrm{,}{75}^1\left(\approx 0\mathrm{,}0469\right)$. Annak a valószínűsége, hogy a megnézett négy reklám közül mind hitelt reklámoz: $\left(\genfrac{}{}{0ex}{}{4}{4}\right)\cdot 0\mathrm{,}{25}^4\cdot 0\mathrm{,}{75}^0\left(\approx 0\mathrm{,}0039\right)$. A kérdéses valószínűség az előbbi valószínűségek összege, így a keresett valószínűség kb. 0,2617.   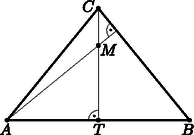3. Egy egyenlő szárú háromszög magasságpontja a háromszög alaphoz tartozó magasságának súlyponttól különböző harmadoló pontja. $a)$ Bizonyítsuk be, hogy a háromszög alapjának fele éppen a magasságpont alaptól vett távolságának és az alaphoz tartozó magasság hosszának mértani közepe.  (7 pont) $b)$ Számítsuk ki a háromszög belső szögeinek nagyságát.  (5 pont)   Megoldás. $a)$ Jelölje az egyenlő szárú háromszög magasságpontját $M$, az alaphoz tartozó magasság talppontját $T$.     A $BC$ oldalhoz tartozó magasságot megrajzolva az $ACT$ háromszög hasonló lesz az $MAT$ háromszöghöz, mert $MTA\sphericalangle =CTA\sphericalangle$ és $MAT\sphericalangle =ACT\sphericalangle$. A hasonlóság miatt $\frac{MT}{AT}=\frac{AT}{CT}$, melyet rendezve $AT=\sqrt[]{MT\cdot CT}$ $\left(AT>0\right)$. Tehát a háromszög alapjának fele valóban a feladat szerinti szakaszok mértani közepe. $b)$ Legyen az egyenlő szárú háromszög alapjának hossza $a$, magasságának hossza $m$. Az $ACT$ és $MAT$ háromszögek hasonlósága miatt $\begin{array}{c}{\displaystyle \frac{\frac{2}{3}m}{\frac{a}{2}}=\frac{\frac{a}{2}}{m}\mathrm{,}\text{melyből}\frac{m}{a}=\frac{\sqrt[]{3}}{2\sqrt[]{2}}\left(a\mathrm{,}m>0\right)\mathrm{.}}\end{array}$ Az egyenlő szárú háromszög alapon fekvő szögeit $\beta$-val, szárszögét $\gamma$-val jelölve a $BCT$ derékszögű háromszögben $\begin{array}{c}{\displaystyle \text{tg}\beta =\frac{m}{\frac{a}{2}}=2\cdot \frac{m}{a}=\frac{\sqrt[]{3}}{\sqrt[]{2}}\mathrm{,}\text{ahonnan}\beta \approx 50\mathrm{,}{77}^{\circ }\mathrm{.}}\end{array}$ A háromszög szárszöge $\gamma ={180}^{\circ }-2\beta \approx 78\mathrm{,}{46}^{\circ }$.   4. Az alábbi táblázatban a tavalyi kézilabda NB I-ben szereplő női csapatok alapszakasz végén elért pontszáma látható.   ${\displaystyle \begin{array}{|ccccccccccccc|}\hline {\displaystyle \text{Csapat száma}}\hfill & \hfill {\displaystyle \text{ 1.}}\hfill & \hfill {\displaystyle \text{ 2.}}\hfill & \hfill {\displaystyle \text{ 3.}}\hfill & \hfill {\displaystyle \text{ 4.}}\hfill & \hfill {\displaystyle \text{ 5.}}\hfill & \hfill {\displaystyle \text{ 6.}}\hfill & \hfill {\displaystyle \text{ 7.}}\hfill & \hfill {\displaystyle \text{ 8.}}\hfill & \hfill {\displaystyle \text{ 9.}}\hfill & \hfill {\displaystyle \text{ 10.}}\hfill & \hfill {\displaystyle \text{ 11.}}\hfill & \hfill {\displaystyle \text{ 12. }}\hfill \\ {\displaystyle \text{Szerzett pont}}\hfill & \hfill {\displaystyle \text{ 41}}\hfill & \hfill {\displaystyle \text{ 41}}\hfill & \hfill {\displaystyle \text{ 31}}\hfill & \hfill {\displaystyle \text{ 31}}\hfill & \hfill {\displaystyle \text{ 28}}\hfill & \hfill {\displaystyle \text{ 20}}\hfill & \hfill {\displaystyle \text{ 20}}\hfill & \hfill {\displaystyle \text{ 19}}\hfill & \hfill {\displaystyle \text{ 15}}\hfill & \hfill {\displaystyle \text{ 9}}\hfill & \hfill {\displaystyle \text{ 5}}\hfill & \hfill {\displaystyle \text{ 4 }}\hfill \\ \hline\end{array}}$   $a)$ Adjuk meg az alábbi állítások logikai értékét (igaz vagy hamis). $•$ Az alapszakaszban átlagosan $22$ pontot értek el a csapatok. $•$ Az elért pontszámok szórása egészre kerekítve $12$ pont.  (3 pont) Az alapszakasz vége után a négy legtöbb pontot elérő csapat a felsőházban, a négy legkevesebb pontot elérő csapat az alsóházban, míg a többi csapat a középházban folytatta küzdelmeit. $b)$ Igaz-e az a megállapítás, hogy az egyes ,,házakban'' lévő csapatok pontszámainak a mediántól vett átlagos abszolút eltéréseinek összege megegyezik az alapszakaszban résztvevő összes csapat pontszámának a legkisebb módusztól vett átlagos abszolút eltérésével?  (5 pont) A kézilabda mérkőzéseken győzelem esetén $2$, döntetlen esetén $1$, vereség esetén $0$ pontot kapnak a csapatok. Az egyik csapatnak a $10$. forduló után csak $11$ pontja volt. $c)$ Hányféleképpen érhette el a csapat a $11$ pontot, ha azt is figyelembe vesszük, hogy milyen sorrendben érte el azt?  (6 pont)   Megoldás. $a)$ A szerzett pontok átlaga: $\begin{array}{c}{\displaystyle \overline{x}=\frac{2\cdot 41+2\cdot 31+28+2\cdot 20+19+15+9+5+4}{12}=\frac{264}{12}=\mathrm{22,}}\end{array}$ tehát az első állítás igaz. A szerzett pontok szórása: $\begin{array}{c}{\displaystyle \sigma =\sqrt[]{\frac{2\cdot {\left(41-22\right)}^2+2\cdot {\left(31-22\right)}^2+\text{...}+{\left(5-22\right)}^2+{\left(4-22\right)}^2}{12}}=\sqrt[]{\frac{1768}{12}}\approx \mathrm{12,}}\end{array}$ tehát a második állítás is igaz. $b)$ Az elért pontszámokat monoton növekvő sorba rendezve az adatok mediánja a két középső elem számtani közepe, vagyis 20 lesz. A legkisebb leggyakrabban előforduló elem (módusz) szintén a 20. A mediántól vett eltérések a felső-, közép- és alsóházban rendre: 21, 21, 11, 11, 8, 0, 0, 1, 5, 11, 15, 16. Az eltérések átlaga a felső-, közép- és alsóházban rendre 16, $\frac{9}{4}$, $\frac{47}{4}$, melyek összege 30. A módusztól vett eltérések megegyeznek a mediántól vett eltérésekkel, melyek átlaga 10. Tehát a megállapítás hamis. $c)$ A csapat 10 forduló után a 11 pontot a pontszámokat tekintve ötféleképpen érhette el: 2-2-2-2-2-1-0-0-0-0; 2-2-2-2-1-1-1-0-0-0; 2-2-2-1-1-1-1-1-0-0; 2-2-1-1-1-1-1-1-1-0; 2-1-1-1-1-1-1-1-1-1. Ha azt is figyelembe vesszük, hogy a 11 pontot milyen sorrendben érte el, akkor a lehetőségek száma az ismétléses permutáció segítségével rendre $\frac{10!}{5!\cdot 4!}$; $\frac{10!}{4!\cdot 3!\cdot 3!}$; $\frac{10!}{3!\cdot 5!\cdot 2!}$; $\frac{10!}{2!\cdot 7!}$; $\frac{10!}{9!}$. Az összes lehetőség száma az előbbi lehetőségek összege, vagyis $\begin{array}{c}{\displaystyle \frac{10!}{5!\cdot 4!}+\frac{10!}{4!\cdot 3!\cdot 3!}+\frac{10!}{3!\cdot 5!\cdot 2!}+\frac{10!}{2!\cdot 7!}+\frac{10!}{9!}=1260+4200+2520+360+10=8350.}\end{array}$ A csapat 10 forduló után 8350-féleképpen érhette el a 11 pontot.   II. rész     5. Adott az $y=-x^2+3x+3$ egyenletű parabola. $a)$ Adjuk meg a parabola tengelypontjának koordinátáit.  (3 pont) $b)$ Számítsuk ki a megadott parabola $x-2y=1$ egyenletű egyenesre illeszkedő húrjának a hosszát.  (6 pont) $c)$ Írja fel a parabola azon érintőjének egyenletét, amely párhuzamos a parabola $3$ és $4$ abszcisszájú pontjait összekötő szakasszal.  (7 pont)   Megoldás. $a)$ Az adott egyenlet jobb oldalát teljes négyzetté alakítva: $\begin{array}{c}{\displaystyle y=-x^2+3x+3=-\left[x^2-3x\right]+3=-\left[{\left(x-\frac{3}{2}\right)}^2-\frac{9}{4}\right]+3=-{\left(x-\frac{3}{2}\right)}^2+\frac{21}{4}\mathrm{,}}\end{array}$ ahonnan a tengelypont koordinátái $T\left(\frac{3}{2};\frac{21}{4}\right)$. $b)$ A húr két végpontjának koordinátáit az alábbi egyenletrendszer megoldásai adják: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =-x^2+3x+\mathrm{3,}}\hfill \\ \hfill {\displaystyle 1}& {\displaystyle =x-2y\mathrm{.}}\hfill \end{array}}$ A második egyenletből $x$-et kifejezve, majd a kapott kifejezést a parabola egyenletébe behelyettesítve rendezés után a $-4y^2+y+5=0$ másodfokú egyenletet kapjuk, melynek gyökei $y_1=-1$ és $y_2=\frac{5}{4}$. A húr végpontjainak koordinátái $A\left(-1;-1\right)$ és $B\left(\frac{7}{2};\frac{5}{4}\right)$, melyből a húr hossza $\begin{array}{c}{\displaystyle h=\sqrt[]{{\left(\frac{7}{2}+1\right)}^2+{\left(\frac{5}{4}+1\right)}^2}=\frac{9}{4}\sqrt[]{5}\approx 5\mathrm{,}03\text{ egység.}}\end{array}$ $c)$ A parabola 3 és 4 abszcisszájú pontjainak koordinátái $P\left(3;3\right)$ és $Q\left(4;-1\right)$. A $P$ és $Q$ pontokon áthaladó egyenes meredeksége a $\overrightarrow{PQ}\left(1;-4\right)$ irányvektorból $m=-4$. Mivel a keresett érintő párhuzamos a $PQ$ egyenessel, ezért az érintő egyenlete $y=-4x+b$ alakú, ahol $b$ értékét keressük. Az előbbi alakban megadott egyenesek közül az lesz érintő, melynek egy közös pontja van a megadott parabolával, tehát az alábbi egyenletrendszernek csak egy számpár megoldása lehet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y}& {\displaystyle =-x^2+3x+\mathrm{3,}}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =-4x+b\mathrm{.}}\hfill \end{array}}$ A két jobb oldali kifejezés egyenlőségéből az $x^2-7x+b-3=0$ paraméteres másodfokú egyenletet kapjuk, melynek pontosan akkor van egy darab valós gyöke, ha a diszkriminánsa 0, azaz ha ${\left(-7\right)}^2-4\left(b-3\right)=0$, ahonnan $b=\frac{61}{4}$. A keresett érintő egyenlete: $y=-4x+\frac{61}{4}$.   6. Egy városban hat tömegközlekedési csomópont található. Az egyes csomópontokból a többi csomópontba bizonyos számú közvetlen járat vezet (két csomópont között csak egy közvetlen járat megy). A csomópontokból induló járatok számának szorzata 60. A közlekedési társaság ellenőrei szeretnének a csomópontok közötti összes vonalon jegyellenőrzést tartani. Az ellenőrök valamelyik csomópontból közösen indulnak, elmennek egy másik csomópontig, majd onnan együtt tovább utaznak egy következőbe. $a)$ A fenti módszert folytatva meg tudják-e úgy szervezni a csomópontok közötti ellenőrzést, hogy minden vonalon pontosan egyszer utazzanak?  (8 pont) Az egyik állomás mozgólépcsőjén állva egy utas $40$ másodperc alatt ér le a föld felszínéről a föld alatti peronra. Ugyanezt az utat $55$ másodperc alatt teszi meg, ha a mozgólépcső nem működik és ő azon egyenletes tempóban lefelé gyalogol. $b)$ Mennyi idő alatt ér le az utas a peronra, ha a mozgólépcső működik, és közben ő azon egyenletesen sétál lefelé?  (8 pont)   Megoldás. $a)$ Jelölje az egyes közlekedési csomópontokból induló közvetlen járatok számát rendre $a$, $b$, $c$, $d$, $e$ és $f$. Ekkor a feladat szövege szerint $a\cdot b\cdot c\cdot d\cdot e\cdot f=60$. A közvetlen járatok számának meghatározásához bontsuk prímtényezők szorzatára a 60-at: $60=2\cdot 2\cdot 3\cdot 5$. A csomópontokat és azok közötti közvetlen járatokat egyszerű gráffal szemléltetve megállapítható, hogy a gráfban az egyes pontok fokszáma legfeljebb 5 lehet, ezért a csúcsok fokszámai csak a következők lehetnek: 1, 1, 2, 2, 3, 5 vagy 1, 1, 1, 3, 4, 5. Utóbbi a fokszámtétel miatt nem lehetséges, előbbi viszont igen, ekkor létezik a feladat feltételeinek megfelelő gráf. A feladatban említett csomópontok közötti ellenőrzést pontosan akkor tudnák végrehajtani az ellenőrök, ha gráfunknak lenne Euler-vonala, ami az Euler-tétel szerint nem lehetséges, így az ellenőrzés a megadott feltételekkel nem végrehajtható. $b)$ Jelölje a mozgólépcső hosszát méterben $l$, a kérdéses időt pedig másodpercben $t^{*}$. Az $s=v\cdot t$ összefüggést felhasználva, a feladat szövege alapján az alábbi táblázat készíthető:   ${\displaystyle \begin{array}{|cccc|}\hline {\displaystyle }\hfill & \hfill {\displaystyle \text{ út}}\hfill & \hfill {\displaystyle \text{ idő}}\hfill & \hfill {\displaystyle \text{ sebesség }}\hfill \\ {\displaystyle \text{ha a vásárló áll és a mozgólépcső működik }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>l</mi></math>}}\hfill & \hfill {\displaystyle \text{ 40}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>l</mi></mrow><mrow><mn>40</mn></mrow></mfrac></mrow></math> }}\hfill \\ {\displaystyle \text{ha a mozgólépcső nem működik, és a vásárló sétál }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>l</mi></math>}}\hfill & \hfill {\displaystyle \text{ 55}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>l</mi></mrow><mrow><mn>55</mn></mrow></mfrac></mrow></math> }}\hfill \\ {\displaystyle \text{ha a mozgólépcső működik, és a vásárló sétál }}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>l</mi></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>t</mi></mrow><mrow><mi>*</mi></mrow></msup></mrow></math>}}\hfill & \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>l</mi></mrow><mrow><mn>40</mn></mrow></mfrac></mrow><mo stretchy="false">+</mo><mrow><mfrac><mrow><mi>l</mi></mrow><mrow><mn>55</mn></mrow></mfrac></mrow></math> }}\hfill \\ \hline\end{array}}$   A kérdéses időt a táblázat utolsó sorából felírva: $\begin{array}{c}{\displaystyle t^{*}=\frac{s}{v}=\frac{l}{\frac{l}{40}+\frac{l}{55}}=\frac{l}{\frac{19l}{440}}=\frac{440}{19}\approx 23\mathrm{,}16\text{ másodperc.}}\end{array}$ Tehát az utas kb. 23 másodperc alatt ér le a peronra, ha a mozgólépcső működik és ő azon egyenletesen sétál lefelé.   7. Egy egyetem közlekedésmérnök szakos hallgatói egy lámpa nélküli forgalmas gyalogátkelőhely mellett figyelik az autósok megállási szokásait. Egy hétfői napon egy adott időszakban a zebrán áthaladó járművek $16\%$-a busz, $24\%$-a motor, $40\%$-a személygépkocsi volt, a többi esetben pedig más jármű haladt át a zebrán. Megfigyelték, hogy a buszsofőrök az esetek $80\%$-ában, a személygépkocsik vezetői $65\%$-ban, a motorosoké $60\%$-ban, míg a többi járművezető $75\%$-ban áll meg a zebra előtt. $a)$ Mekkora annak a valószínűsége, hogy ha egy gyalogos lelép a zebrára, megáll a zebra előtt közlekedő jármű?  (6 pont) Zsuzsa nénit a zebrán majdnem elütötte egy jármű, ami nem állt meg. $b)$ Mekkora annak a valószínűsége, hogy a jármű motor volt?  (7 pont) A sok baleset miatt a hatóság úgy döntött, hogy jelzőlámpát szerelnek fel a gyalogátkelőhelyhez, mely reggel $6$ óra és este $8$ óra között $2$ perc $15$ másodpercenként vált zöldre. Este $8$ órától reggel $6$ óráig a lámpa nem működik, ekkor sárgán villog. $c)$ Hányszor vált zöldre a lámpa egy nap alatt, ha az első váltás mindig a bekapcsoláskor, pontban $6$ órakor történik?  (3 pont)   Megoldás. $a)$ Jelölje $A$ azt az eseményt, hogy a zebra előtt közlekedő jármű megáll, $B_1$, $B_2$, $B_3$ és $B_4$ pedig rendre azt, hogy a zebra elé érkező jármű busz, motor, személygépkocsi, illetve más. Ekkor a feladat szövege alapján: $P\left(A\mid B_1\right)=0\mathrm{,}8$, $P\left(A\mid B_2\right)=0\mathrm{,}6$, $P\left(A\mid B_3\right)=0\mathrm{,}65$, $P\left(A\mid B_4\right)=0\mathrm{,}75$, valamint $P\left(B_1\right)=0\mathrm{,}16$, $P\left(B_2\right)=0\mathrm{,}24$, $P\left(B_3\right)=0\mathrm{,}4$, $P\left(B_4\right)=0\mathrm{,}2$. A feladat szerint $P\left(A\right)$ valószínűségét keressük, melynek értéke: $\begin{array}{c}{\displaystyle P\left(A\right)=0\mathrm{,}8\cdot 0\mathrm{,}16+0\mathrm{,}6\cdot 0\mathrm{,}24+0\mathrm{,}65\cdot 0\mathrm{,}4+0\mathrm{,}75\cdot 0\mathrm{,}2=0\mathrm{,}682.}\end{array}$ Tehát annak a valószínűsége, hogy a zebra előtt közlekedő jármű megáll 0,682. $b)$ I. megoldás. A feladat szövege alapján a következő feltételes valószínűségeket írhatjuk fel: $\begin{array}{c}{\displaystyle P\left(\overline{A}\mid B_1\right)=0\mathrm{,}\mathrm{2,}P\left(\overline{A}\mid B_2\right)=0\mathrm{,}\mathrm{4,}P\left(\overline{A}\mid B_3\right)=0\mathrm{,}\mathrm{35,}P\left(\overline{A}\mid B_4\right)=0\mathrm{,}25.}\end{array}$ A Bayes-tétel alapján annak a valószínűsége, hogy a meg nem álló jármű motor volt: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(B_2\mid \overline{A}\right)}& {\displaystyle ={\displaystyle \frac{P\left(\overline{A}\mid B_2\right)\cdot P\left(B_2\right)}{\sum _{i=1}^{4}P\left(\overline{A}\mid B_i\right)\cdot P\left(B_i\right)}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\displaystyle \frac{0\mathrm{,}4\cdot 0\mathrm{,}24}{0\mathrm{,}2\cdot 0\mathrm{,}16+0\mathrm{,}4\cdot 0\mathrm{,}24+0\mathrm{,}35\cdot 0\mathrm{,}4+0\mathrm{,}25\cdot 0\mathrm{,}2}}\approx 0\mathrm{,}3019.}\hfill \end{array}}$ Tehát a keresett valószínűség kb. 0,3019. II. megoldás. Tekintsünk 1000 db zebrán áthaladó járművet. Ekkor a járművek között 160 db busz, 240 db motor, 400 db személygépkocsi és 200 db más van. A feladat szövege alapján a meg nem álló buszok, motorok, személygépkocsik és más járművek száma rendre 32, 96, 140 és 50. A meg nem álló motorosok száma 96, mely az összes meg nem álló jármű $\frac{96}{32+96+140+50}=\frac{96}{318}\approx 0\mathrm{,}3019$-ed része. A kiszámított arány független a konkrét darabszámtól, az csupán az eloszlástól függ, így a keresett valószínűség kb. 0,3019. $c)$ Reggel 6 és este 8 óra között 14 óra, azaz 840 perc telik el. A lámpa 2,25 percenként vált zöldre, így a megadott időintervallumban a zöldre váltások száma: $\begin{array}{c}{\displaystyle n=\left[\frac{840}{2\mathrm{,}25}\right]+1=374.}\end{array}$   8. Kovács úr az újonnan épített házába az ábrán látható félköríves ablakot szeretné beépíteni. Az ablak félköríves része opálüvegből készült, mely egységnyi felületen feleannyi fényt enged át, mint a tisztán átlátszó téglalap alakú rész. Az $ABCD$ téglalap, amibe az ablakot beilleszti 6 méter kerületű. Milyen széles és magas a beépített ablak, ha az a lehető legtöbb fényt engedi be a lakásba?  (16 pont)       I. megoldás. Az ablak tisztán átlátszó téglalap alakú részének szélességét $a$-val, magasságát $b$-vel jelölve az $ABCD$ téglalap kerülete $3a+2b=6$. Mivel az ablakon átjövő fény mennyisége egyenesen arányos a felülettel, ezért a $\begin{array}{c}{\displaystyle V\left(a;b\right)=2ab+\frac{{\left(\frac{a}{2}\right)}^2\cdot \pi }{2}}\end{array}$ függvény maximumát keressük. A $3a+2b=6$ kifejezésből $b=3-\frac{3}{2}a$ helyettesítéssel a világosságot megadó másodfokú függvény $\begin{array}{c}{\displaystyle V\left(a\right)=-3a^2+\frac{a^2}{8}\pi +6a\mathrm{,}}\end{array}$ melynek zérushelyei $a_1=0$ és $a_2=\frac{6}{3-\frac{\pi }{8}}$. Mivel $V$ főegyütthatója negatív, ezért függvényünknek valóban maximuma lesz, melyet a zérushelyek számtani közepénél vesz fel. A $V$ függvény maximumhelye tehát $a=\frac{6}{6-\frac{\pi }{4}}\approx 1\mathrm{,}15$ m. $a$ értékét a $b=3-\frac{3}{2}a$ összefüggésbe visszahelyettesítve $b\approx 1\mathrm{,}27$ (m). A beépített ablak tehát kb. 115 cm széles és kb. 185 cm magas.   II. megoldás. Az ablak tisztán átlátszó téglalap alakú részének szélességét $a$-val, magasságát $b$-vel jelölve az $ABCD$ téglalap kerülete $3a+2b=6$. Mivel az ablakon átjövő fény mennyisége egyenesen arányos a felülettel, ezért a $\begin{array}{c}{\displaystyle V\left(a;b\right)=2ab+\frac{{\left(\frac{a}{2}\right)}^2\cdot \pi }{2}}\end{array}$ függvény maximumát keressük. A $3a+2b=6$ kifejezésből $b=3-\frac{3}{2}a$ helyettesítéssel a világosságot megadó függvény $\begin{array}{c}{\displaystyle V\left(a\right)=6a-3a^2+\frac{a^2}{8}\pi }\end{array}$ alakba írható, melynek akkor lehet szélsőértéke, ha első deriváltja 0. A függvényt deriválva $V\text{'}\left(a\right)=6-6a+a\frac{\pi }{4}$, melyből $\begin{array}{c}{\displaystyle a=\frac{6}{6-\frac{\pi }{4}}\approx 1\mathrm{,}15\text{m. }}\end{array}$ Az $a=\frac{6}{6-\frac{\pi }{4}}$ helyen $V\text{'}$ előjelet $\left(+\to -\right)$ vált, tehát $V$-nek $a$-ban valóban maximuma van. $a$ értékét a $b=3-\frac{3}{2}a$ összefüggésbe visszahelyettesítve $b\approx 1\mathrm{,}27$ (m). A beépített ablak tehát kb. 115 cm széles és kb. 185 cm magas.   9. Egy hazai gyorsétterem csonkakúp alakú kávéspohárban szolgálja fel a kávét. A 9 cm magas pohárba magassága feléig töltik a presszókávét, melyet zárható, hőálló fedéllel látnak el, hogy a kávé biztosan ne tudjon kiborulni. A pohár alsó, kisebbik alapkörének belső átmérője 4,5 cm, míg a felső, nagyobbé 7 cm. Milyen magasan lesz a pohárban a kávé, ha a poharat megfordítva a nagyobb alapjára állítjuk?  (16 pont)   Megoldás. Készítsünk síkmetszetet a csonkakúp alakú kávéspohárról, majd számítsuk ki a kávé térfogatát (1. ábra).   1. 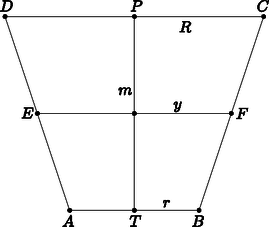ábra   A pohárban lévő kávé térfogata a csonkakúp térfogatának képletéből: $\begin{array}{c}{\displaystyle V_{\text{kávé}}=\frac{\left(r^2+y^2+r\cdot y\right)\cdot m\cdot \pi }{6}=\frac{\left(2\mathrm{,}{25}^2+2\mathrm{,}{875}^2+2\mathrm{,}25\cdot 2\mathrm{,}875\right)\cdot 9\cdot \pi }{6}\approx 93\mathrm{,}3\left({\text{cm}}^3\right)\mathrm{.}}\end{array}$ Ha a poharat megfordítjuk, azaz a nagyobb alapjára állítjuk, a kávé térfogata nem változik, így a megfelelő térfogatok felírása után meghatározható a keresett magasság. Egészítsük ki a megfordított csonkakúpot forgáskúppá, készítsünk síkmetszetet, majd számítsuk ki az egyes részek térfogatait (2. ábra).   2. ábra   Az $OMB$ háromszög hasonló az $OPC$ háromszöghöz, mert megfelelő szögeik egyenlők. A kiegészítő kiskúp magasságát $x$-szel jelölve a hasonlóság miatt $\frac{x}{r}=\frac{x+9}{R}$, vagyis $\frac{x}{2\mathrm{,}25}=\frac{x+9}{3\mathrm{,}5}$, ahonnan $x=16\mathrm{,}2$ (cm). A kiegészítő kiskúp térfogata az előbbiek szerint: $\begin{array}{c}{\displaystyle V_{\text{kiskúp}}=\frac{r^2\cdot \pi \cdot x}{3}=\frac{2\mathrm{,}{25}^2\cdot \pi \cdot 16\mathrm{,}2}{3}\approx 85\mathrm{,}9\left({\text{cm}}^3\right)\mathrm{,}}\end{array}$ a teljes forgáskúp térfogata: $\begin{array}{c}{\displaystyle V_{\text{teljes}}=\frac{R^2\cdot \pi \cdot \left(x+9\right)}{3}=\frac{3\mathrm{,}{5}^2\cdot \pi \cdot 25\mathrm{,}2}{3}\approx 323\mathrm{,}3\left({\text{cm}}^3\right)\mathrm{,}}\end{array}$ melyekből a pohár térfogata $V_{\text{pohár}}=V_{\text{teljes}}-V_{\text{kiskúp}}\approx 237\mathrm{,}4\left({\text{cm}}^3\right)$. Ha a pohár térfogatából kivonjuk a kávé térfogatát, megkapjuk a kimaradó rész térfogatát, ami $V_{\text{kimaradó}}=V_{\text{pohár}}-V_{\text{kávé}}\approx 144\mathrm{,}1\left({\text{cm}}^3\right)$. A kávé magasságának meghatározásához használjuk a hasonló testek térfogatának arányára vonatkozó tételt. A kiegészítő kiskúp középpontosan hasonló ahhoz a forgáskúphoz, amelyet úgy kapunk, hogy a teljes forgáskúpból elhagyjuk a kávét tartalmazó részt, így a térfogatok arányát felírva $\begin{array}{c}{\displaystyle \frac{V_{\text{kiskúp}}}{V_{\text{kiskúp}+\text{kimaradó}}}={\left(\frac{16\mathrm{,}2}{25\mathrm{,}2-m}\right)}^3\mathrm{,}\text{melyből}m\approx 2\mathrm{,}7\text{cm. }}\end{array}$ Tehát a megfordított pohárban kb. 2,7 cm magasan áll a kávé.