Cím:	Megoldásvázlatok a 2017/3. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Katz Sándor
Füzet:	2017/április, 204 - 212. oldal	PDF  |  MathML
Hivatkozás(ok):	2017/március: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg a következő egyenleteket a valós számok halmazán: $a)$ $\sqrt[]{x^2-6x+9}=3-x$,  (3 pont) $b)$ $2\sqrt[]{1-\text{cos}{}^{2}x}=\text{tg}x$.  (7 pont)   Megoldás. $a)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \sqrt[]{x^2-6x+9}}& {\displaystyle =3-x\mathrm{,}}\hfill \\ \hfill {\displaystyle \sqrt[]{{\left(3-x\right)}^2}}& {\displaystyle =3-x\mathrm{,}}\hfill \\ \hfill {\displaystyle |3-x|}& {\displaystyle =3-x\mathrm{.}}\hfill \end{array}}$ Ez akkor és csak akkor teljesül, ha $3-x\ge 0$, azaz $x\le 3$. Tehát az egyenlet megoldása minden 3-nál nem nagyobb valós szám. $b)$ ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\sqrt[]{1-\text{cos}{}^{2}x}}& {\displaystyle =\text{tg}x\mathrm{,}}\hfill \\ \hfill {\displaystyle 2\sqrt[]{\text{sin}{}^{2}x}}& {\displaystyle =\frac{\text{sin}x}{\text{cos}x}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2|\text{sin}x|}& {\displaystyle =\frac{\text{sin}x}{\text{cos}x}\mathrm{,}}\hfill \\ \hfill {\displaystyle 2|\text{sin}x|-\frac{\text{sin}x}{\text{cos}x}}& {\displaystyle =0.}\hfill \end{array}}$ Ha $\text{sin}x\ge 0$, azaz $\begin{array}{c}{\displaystyle 2k\pi \le x\le \pi +2k\pi \mathrm{,}}\end{array}$ ($*$) ahol $k\in \text{Z}$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\text{sin}x-\frac{\text{sin}x}{\text{cos}x}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{sin}x\left(2-\frac{1}{\text{cos}x}\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{sin}x=\mathrm{0,}\text{vagy}}& {\displaystyle \text{cos}x=0\mathrm{,}5.}\hfill \end{array}}$ A $\left(*\right)$ feltételt is figyelembe véve $x=k\pi$, vagy $x=\frac{\pi }{3}+2k\pi$, ahol $k\in \text{Z}$. Ha $\text{sin}x<0$, azaz $\begin{array}{c}{\displaystyle \pi +2k\pi <x<2\pi +2k\pi \mathrm{,}}\end{array}$ ($**$) ahol $k\in \text{Z}$, akkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle -2\text{sin}x-\frac{\text{sin}x}{\text{cos}x}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle -\text{sin}x\left(2+\frac{1}{\text{cos}x}\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{sin}x=\mathrm{0,}\text{vagy}}& {\displaystyle \text{cos}x=-0\mathrm{,}5.}\hfill \end{array}}$ A $\left(**\right)$ feltételt is figyelembe véve $x=\frac{4\pi }{3}+2k\pi$, ahol $k\in \text{Z}$.   2. 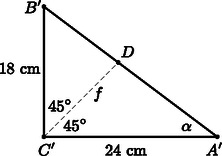Az $ABC$ derékszögű háromszög befogói $BC=6\text{cm}$ és $AC=8\text{cm}$. A hozzá hasonló $A\text{'}B\text{'}C\text{'}$ háromszög $A\text{'}B\text{'}$ átfogója 30 cm. Mekkora az $A\text{'}B\text{'}C\text{'}$ háromszög területe, a $C\text{'}$ csúcsból induló magassága, súlyvonala és szögfelezője?  (12 pont)   Megoldás. Az $ABC$ háromszög átfogója 10 cm, területe $t=24{\text{cm}}^2$. Ezért a nagyítás aránya $k=3$. Így az $A\text{'}B\text{'}C\text{'}$ területe $t\text{'}=k^2\cdot t=216{\text{cm}}^2$. $\begin{array}{c}{\displaystyle m_{c\text{'}}=\frac{2t\text{'}}{c\text{'}}=\frac{2\cdot 216{\text{cm}}^2}{30\text{cm}}=\frac{216}{15}\text{cm}=14\mathrm{,}4\text{cm}\mathrm{,}{s}_{c\text{'}}=\frac{c\text{'}}{2}=15\text{cm.}}\end{array}$     Az $f$ szögfelezőt az $A\text{'}DC\text{'}$ és $B\text{'}DC\text{'}$ háromszögek területének felhasználásával számoljuk ki: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle }& {\displaystyle }\hfill & {\displaystyle T_{A\text{'}B\text{'}C\text{'}▵}=T_{A\text{'}DC\text{'}▵}+T_{B\text{'}DC\text{'}▵}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle \frac{1}{2}\cdot f\cdot 24\text{cm}\cdot \text{sin}{45}^{\circ }+\frac{1}{2}\cdot f\cdot 18\text{cm}\cdot \text{sin}{45}^{\circ }=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =}\hfill & {\displaystyle 216{\text{cm}}^2\mathrm{.}}\hfill \end{array}}$ Ebből $\begin{array}{c}{\displaystyle f=\frac{2\cdot 216{\text{cm}}^2}{42\text{cm}\cdot \frac{\sqrt[]{2}}{2}}=\frac{216\cdot \sqrt[]{2}}{21}\text{cm}\approx 14\mathrm{,}55\text{cm}\mathrm{.}}\end{array}$   II. megoldás a szögfelező kiszámítására. Az $A\text{'}B\text{'}C\text{'}$ háromszögben $\text{sin}\alpha =\frac{18}{30}=0\mathrm{,}6\Rightarrow \alpha =36\mathrm{,}{87}^{\circ }$. $C\text{'}DA\text{'}\sphericalangle ={180}^{\circ }-\left({45}^{\circ }+\alpha \right)=98\mathrm{,}{13}^{\circ }$. Az $A\text{'}DC\text{'}$ háromszögben $\frac{f}{24\text{cm}}=\frac{\text{sin}36\mathrm{,}{87}^{\circ }}{\text{sin}98\mathrm{,}{13}^{\circ }}$. Ebből $f\approx 14\mathrm{,}55$ cm.   III. megoldás a szögfelező kiszámítására. Szögfelező tétel szerint $B\text{'}D:DA\text{'}=18:24$. Ebből $B\text{'}D=90/7$ cm. Koszinusztétel a $B\text{'}DC\text{'}$ háromszögben: ${\left(90/7\right)}^2=f^2+{18}^2-2f\cdot 18\text{cos}{45}^{\circ }$. Ennek két megoldása $f_1=14\mathrm{,}55$ cm és $f_2=10\mathrm{,}91$ cm. Csak az első a jó megoldás, mert $f$ nem lehet kisebb $m_c$-nél.   3. Oldjuk meg a valós számok halmazán: $a)$ $x^2+3\ge 4x$,  (3 pont) $b)$ ${\displaystyle \frac{x^2-4x+3}{x}}\ge 0$,  (3 pont) $c)$ $x^2-4x+{\displaystyle \frac{3}{{\left(x-2\right)}^2}}=0$.  (9 pont)   Megoldás. $a)$ Az $f\left(x\right)=x^2-4x+3$ függvény két zérushelye $x_1=1$, $x_2=3$, $f\left(x\right)\ge 0$, ha $x\le 1$, vagy $x\ge 3$. $b)$ Az értelmezési tartomány: $x\ne 0$. A tört nemnegatív, ha a számláló és a nevező azonos előjelű, illetve ha a számláló 0. Ez $0<x\le 1$, illetve $x\ge 3$ esetén teljesül. $c)$ Értelmezési tartomány: $\begin{array}{c}{\displaystyle x\ne 2.}\end{array}$ ($*$) Legyen $y={\left(x-2\right)}^2$, ekkor $x^2-4x=y-4$, az egyenlet $\begin{array}{c}{\displaystyle y-4+\frac{3}{y}=0\Rightarrow y^2-4y+3=0.}\end{array}$ Ennek megoldásai $y_1=1$, $y_2=3$. A hozzájuk tartozó $x$-ek: $x_1=3$, $x_2=1$, $x_3=2+\sqrt[]{3}$, $x_4=2-\sqrt[]{3}$. Az $y={\left(x-2\right)}^2$-tel való beszorzás kivételével a lépések ekvivalens átalakítások voltak. A kapott gyökök nem esnek egybe $\left(*\right)$-gal, ezért mind a négy gyök jó.   Második megoldás a $c)$ feladatra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x^2-4x+\frac{3}{{\left(x-2\right)}^2}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle x^2-4x+\frac{3}{x^2-4x+4}}& {\displaystyle =0.}\hfill \end{array}}$ A nevezővel beszorozva: $\begin{array}{c}{\displaystyle x^4-8x^3+20x^2-16x+3=0.}\end{array}$ Észrevéve, hogy $x_1=1$ és $x_2=3$ megoldások, az egyenlet szorzattá alakítható: $\begin{array}{c}{\displaystyle \left(x-1\right)\left(x-3\right)\left(x^2-4x+1\right)=0.}\end{array}$ Az $x^2-4x+1=0$ egyenlet megoldásai $x_3=2+\sqrt[]{3}$, $x_4=2-\sqrt[]{3}$. A kapott gyökök jók.   4. 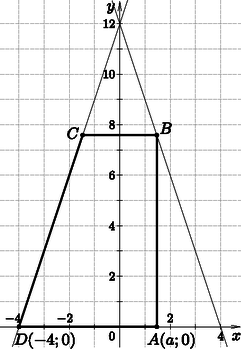Az $y=3x+12$, az $y=-3x+12$ egyenesek és az $x$ tengely által határolt háromszögbe az ábra szerint az $ABCD$ derékszögű trapézt írjuk. Hogyan válasszuk meg az $A\left(a;0\right)$ pontot, hogy a trapéz területe maximális legyen? Mekkora ez a maximális terület?  (14 pont)       Megoldás. A $B$ pont illeszkedik az $y=-3x+12$ egyenesre, ezért koordinátái: $B\left(a;12-3a\right)$, a többi csúcs $C\left(-a;12-3a\right)$ és $D\left(-4;0\right)$. A trapéz alapjai $4+a$ és $2a$, magassága $12-3a$, ezért területe $\begin{array}{c}{\displaystyle t=\frac{\left(4+3a\right)\left(12-3a\right)}{2}\mathrm{.}}\end{array}$ ($*$) A számlálóban a két tényező összege állandó, ezért a számtani és mértani közép összefüggése szerint: $\begin{array}{c}{\displaystyle t=\frac{\left(4+3a\right)\left(12-3a\right)}{2}\le \frac{{\left(\frac{4+3a+12-3a}{2}\right)}^2}{2}=32.}\end{array}$ Látható, hogy $t$ nem lehet nagyobb 32-nél, ennyi akkor és csak akkor lehet, ha $4+3a=12-3a\Rightarrow a=4/3$. Tehát $a=4/3$ esetén lesz a trapéz területe a legnagyobb, ennek értéke $t=32$.   Második megoldás $\left(*\right)$-tól. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t}& {\displaystyle =\frac{\left(4+3a\right)\left(12-3a\right)}{2}=-\frac{9}{2}{a}^2+12a+24=-\frac{9}{2}\left(a^2-\frac{8}{3}a\right)+24=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =-\frac{9}{2}\left[{\left(a-\frac{4}{3}\right)}^2-\frac{16}{9}\right]+24=-\frac{9}{2}{\left(a-\frac{4}{3}\right)}^2+32.}\hfill \end{array}}$ $-\frac{9}{2}{\left(a-\frac{4}{3}\right)}^2\le 0$, ezért $t$ nem lehet nagyobb 32-nél, ennyi akkor és csak akkor lehet, ha $a=4/3$.   Harmadik megoldás $\left(*\right)$-tól. A $\begin{array}{c}{\displaystyle t\left(a\right)=\frac{\left(4+3a\right)\left(12-3a\right)}{2}=\left(-\frac{9}{2}{a}^2+12a+24\right)}\end{array}$ másodfokú függvény két zérushelye a szorzat alakból könnyen leolvasható: $a_1=-\frac{4}{3}$ és $a_2=4$. A függvény szélsőértéke a két zérushely számtani közepénél, $a=\frac{4}{3}$-nál van, $t\left(\frac{4}{3}\right)=32$. Mivel ez pozitív, ezért ez $t$ maximuma. (Vagy azért van itt maximum, mert a polinom alakból látható, hogy a másodfokú tag együtthatója negatív.)   Negyedik megoldás $\left(*\right)$-tól. $\begin{array}{c}{\displaystyle t\left(a\right)=\frac{\left(4+3a\right)\left(12-3a\right)}{2}=-\frac{9}{2}{a}^2+12a+24.}\end{array}$ $t\text{'}\left(a\right)=-9a+12$. Ennek zérushelye $a=4/3$-nál van. Mivel a $t\left(a\right)$ másodfokú függvényben a másodfokú tag előjele negatív, ezért a derivált zérushelyénél a függvénynek maximuma van. Ennek értéke $t\left(\frac{4}{3}\right)=32$.   II. rész     5. 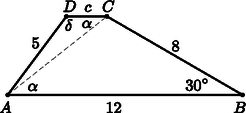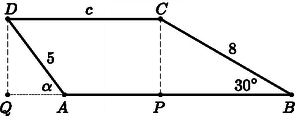Az $ABCD$ trapéz $AB$ alapja 12 cm, a szárak: $BC=8\text{cm}$ és $DA=5\text{cm}$. Az $ABC$ szög ${30}^{\circ }$-os. Mekkora a $CD$ oldal, és a trapéz többi szöge? A $CD$ oldal hosszát cm-ben, a szögeket fokokban, két tizedes jegy pontossággal adjuk meg.  (16 pont)   Megoldás. A $CBE$ háromszögben $\frac{\text{sin}\alpha }{\text{sin}{30}^{\circ }}=\frac{8}{5}$. Ebből $\text{sin}\alpha =0\mathrm{,}8$, ${\alpha }_1=53\mathrm{,}{13}^{\circ }$, vagy ${\alpha }_2=126\mathrm{,}{87}^{\circ }$. Mindkettő jó megoldás. A hozzájuk tartozó $ECB$ szög: ha $\alpha =53\mathrm{,}{13}^{\circ }$, akkor $ADC\sphericalangle =126\mathrm{,}{87}^{\circ }$, $DCB\sphericalangle ={150}^{\circ }$, $\begin{array}{c}{\displaystyle \frac{12-c}{5}=\frac{\text{sin}{96\mathrm{,}87}^{\circ }}{\text{sin}{30}^{\circ }}\Rightarrow c=2\mathrm{,}07\text{cm. }}\end{array}$     Ha $\alpha =126\mathrm{,}{87}^{\circ }$, akkor $ADC\sphericalangle =53\mathrm{,}{13}^{\circ }$, $DCB\sphericalangle ={150}^{\circ }$, $\begin{array}{c}{\displaystyle \frac{12-c}{5}=\frac{\text{sin}{23\mathrm{,}13}^{\circ }}{\text{sin}{30}^{\circ }}\Rightarrow c=8\mathrm{,}07\text{cm. }}\end{array}$   Második megoldás. Az $ABC$ háromszögből koszinusztétellel: $\begin{array}{c}{\displaystyle CA=\sqrt[]{41\mathrm{,}72}=6\mathrm{,}46\text{cm. }}\end{array}$ Szinusztétellel $\frac{\text{sin}\alpha }{\text{sin}{30}^{\circ }}=\frac{8}{6\mathrm{,}46}$, $\text{sin}\alpha =0\mathrm{,}6193$.     Mivel $\alpha$ nem a legnagyobb oldallal van szemben, ezért csak hegyesszög lehet: $\begin{array}{c}{\displaystyle \alpha =CAB\sphericalangle =38\mathrm{,}{26}^{\circ }=ACD\sphericalangle \mathrm{.}}\end{array}$ Az $ADC$ háromszögből szinusztétellel $\frac{\text{sin}\delta }{\text{sin}{38\mathrm{,}26}^{\circ }}=\frac{6\mathrm{,}46}{5}$, $\text{sin}\delta =0\mathrm{,}8$. Nagyobb oldallal szemben hegyes- és tompaszög is lehet: $ADC\sphericalangle =126\mathrm{,}{87}^{\circ }$, $DAB\sphericalangle =53\mathrm{,}{13}^{\circ }$, $DAC\sphericalangle =14\mathrm{,}{87}^{\circ }$, újabb szinusztétellel $c_1=2\mathrm{,}07$ cm, $DCB\sphericalangle ={150}^{\circ }$. $ADC\sphericalangle =53\mathrm{,}{13}^{\circ }$, $DAB\sphericalangle =126\mathrm{,}{87}^{\circ }$, $DAC\sphericalangle =88\mathrm{,}{61}^{\circ }$, újabb szinusztétellel $c_2=8\mathrm{,}07$ cm, $DCB\sphericalangle ={150}^{\circ }$.   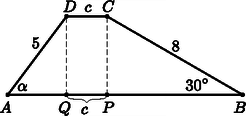Harmadik megoldás. A trapézt magasságaival egy téglalapra és két derékszögű háromszögre bontjuk. Itt egyszerűbbek a számítások, de előre tudni kell, hogy két megoldás lehet.     I. ${\displaystyle \begin{array}{c}\hfill {\displaystyle PC=8\text{cm}\cdot \text{sin}{30}^{\circ }=4\text{cm,<br> PB= 8 <span style="font-weight: normal;font-style: normal;">cm</span><math xmlns="http://www.w3.org/1998/Math/MathML"><mo>⋅</mo></math><span style="font-weight: normal;font-style: normal;">cos</span><math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mn>30</mn></mrow><mrow><mo>∘</mo></mrow></msup></mrow></math>= 6,93 }\text{cm,}}\hfill \\ \hfill {\displaystyle DQ=CP=4\text{cm}\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow AQ=\sqrt[]{5^5-4^2}=3\text{cm}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =QP=12\text{cm}-6\mathrm{,}93\text{cm}-3\text{cm}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\mathrm{,}07\text{cm}\mathrm{,}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle \text{sin}BAD\sphericalangle =4/5\Rightarrow \alpha =53\mathrm{,}{13}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle ADC\sphericalangle =126\mathrm{,}{87}^{\circ }\mathrm{,}DCB\sphericalangle ={150}^{\circ }\mathrm{.}}\hfill \end{array}}$     II. ${\displaystyle \begin{array}{c}\hfill {\displaystyle PC=8\text{cm}\cdot \text{sin}{30}^{\circ }=4\text{cm}\mathrm{,}}\hfill \\ \hfill {\displaystyle PB=8\text{cm}\cdot \text{cos}{30}^{\circ }=6\mathrm{,}93\text{cm}\mathrm{,}}\hfill \\ \hfill {\displaystyle DQ=CP=4\text{cm}\Rightarrow }\hfill \\ \hfill {\displaystyle \Rightarrow AQ=\sqrt[]{5^5-4^2}=3\text{cm}\mathrm{,}}\hfill \\ \hfill {\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =QP=12\text{cm}+3\text{cm}-6\mathrm{,}93\text{cm}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =8\mathrm{,}07\text{cm}\mathrm{,}}\hfill \end{array}}}\hfill \\ \hfill {\displaystyle \text{sin}QAD\sphericalangle =4/5\Rightarrow \alpha =53\mathrm{,}{13}^{\circ }=ADC\sphericalangle \mathrm{,}}\hfill \\ \hfill {\displaystyle DAB\sphericalangle =126\mathrm{,}{87}^{\circ }\mathrm{,}DCB\sphericalangle ={150}^{\circ }\mathrm{.}}\hfill \end{array}}$   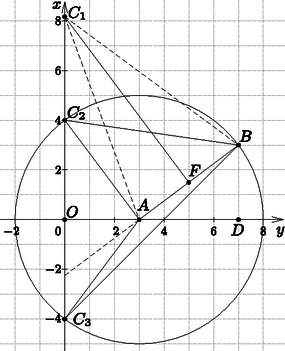6. A pozitív körüljárású, egyenlő szárú $ABC$ háromszög két csúcsa $A\left(3;0\right)$ és $B\left(7;3\right)$. A $C$ csúcs az $y$ tengelyen van. Határozzuk meg a $C$ csúcs koordinátáit, és a háromszög területét.  (16 pont)   Megoldás. Ha $CA=CB$, akkor $C$ illeszkedik $AB$ felező merőlegesére. $\begin{array}{c}{\displaystyle F\left(5;1\mathrm{,}5\right)\mathrm{,}\overrightarrow{AB}\left(4;3\right)\Rightarrow f_{AB}:4x+3y=24\mathrm{,}5.}\end{array}$ Ennek az $y$ tengelyen levő pontja $C_1\left(0;\frac{49}{6}\right)$.     $AB=5$. Ha $AC=AB=5$, akkor $C$ illeszkedik az $A$ középpontú 5 sugarú ${\left(x-3\right)}^2+y^2=25$ körre. Ennek az $y$ tengelyen levő pontjai $C_2\left(0;4\right)$ és $C_3\left(0;-4\right)$. $C_3$ esetén nem pozitív körüljárású a háromszög. $B$ és az $y$ tengely távolsága 7, ezért $BC=BA$ nem lehet. $\begin{array}{c}{\displaystyle F{C}_1=\frac{25}{3}\mathrm{,}\text{így}{T}_{AB{C}_1}=\frac{5\cdot \frac{25}{3}}{2}=\frac{125}{6}\mathrm{.}}\end{array}$ $\overrightarrow{AB}\left(4;3\right)$, $\overrightarrow{A{C}_2}\left(-3;4\right)$, szorzatuk 0, ezért az $AB{C}_2$ háromszög derékszögű, $\begin{array}{c}{\displaystyle T_{AB{C}_2}=\frac{5\cdot 5}{2}=\frac{25}{2}\mathrm{.}}\end{array}$   Megjegyzés. Lehet az $AB{C}_1$ és $AB{C}_2$ háromszögek területét úgy is számolni, hogy az $ODB{C}_1$, illetve az $ODB{C}_2$ derékszögű trapéz területéből levonjuk a megfelelő derékszögű háromszögek területét.   7. Az $a$ paraméter mely értékei esetén van pontosan egy megoldása a következő egyenletnek? $\begin{array}{c}{\displaystyle {25}^x-\left(a-1\right)5^x+2a+3=0.}\end{array}$ (1)  (16 pont)   Megoldás. Legyen $t=5^x$. (1)-nek akkor és csak akkor van pontosan egy gyöke, ha a $t^2-\left(a-1\right)t+2a+3=0$ egyenletnek $a)$ egy gyöke van és az pozitív, vagy $b)$ két gyöke van és azok közül pontosan egy pozitív. $a)$ $D=a^2-10a-11=0$, ebből $a=-1$, ekkor $t=-1$, ez nem jó, vagy $a=11$, ekkor $t=5$, ez jó, (1)-ből $x=1$. $b)$ $D>0$ és $2a+3<0$ esetén $t$-re egy pozitív és egy negatív gyök van. $D>0$, ha $a<-1$, vagy $a>11$. $2a+3<0$, ha $a<-3/2$. Ennek közös része $a<-3/2$. Ha $2a+3=0$, akkor az egyik gyök $t_1=0$, de a másik negatív, ezért ez nem lehet. Tehát (1)-nek pontosan egy gyöke van, ha $a=11$, vagy $a<-3/2$.   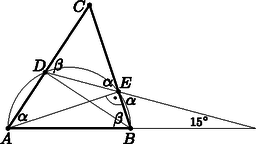8. Az $ABC$ háromszög $AB$ oldala, mint átmérő köré írt kör az $AC$ és $BC$ oldalakat a $D$ és $E$ pontokban metszi. A $DE$ egyenes felezi az $ABC$ háromszög területét, és az $AB$ egyenessel ${15}^{\circ }$-os szöget zár be. Mekkorák az $ABC$ háromszög szögei?  (16 pont)       Megoldás. $ABED$ húrnégyszög, ezért $DEC\sphericalangle =DAB\sphericalangle$ és $CDE\sphericalangle =ABE\sphericalangle$, így $EDC▵\sim ABC▵$. Ha $T_{EDC▵}=1/2\cdot T_{ABC▵}$, akkor a hasonlóság aránya $1/\sqrt[]{2}$. Ezért a két hasonló háromszögben pl. a $\beta$ szöggel szemközti oldalak aránya $1/\sqrt[]{2}$, így az $AEC$ derékszögű háromszögben a $CE$ befogó $1/\sqrt[]{2}$-szöröse az $AC$ átfogónak, emiatt $ECA\sphericalangle ={45}^{\circ }$. Az $ABC▵$-ben $\alpha +\beta ={135}^{\circ }$, $\beta$ pedig a $BEF▵$ külső szöge, ezért $\beta =\alpha +{15}^{\circ }$. Ezekből $\alpha ={60}^{\circ }$ és $\beta ={75}^{\circ }$.   9. $a)$ Hány olyan négyjegyű szám van, amelyben kétféle számjegy szerepel, és mindegyik kétszer?  (3 pont) $b)$ Ha az ilyen típusú számok közül véletlenszerűen kiválasztunk egyet, akkor mennyi a valószínűsége, hogy $4$-gyel osztható számot választunk?  (6 pont) $c)$ Mely $n$ természetes szám, és $x$ és $y$ számjegyekre lesz $\begin{array}{c}{\displaystyle 1+2+3+\text{...}+n=\overline{xyxy}?}\end{array}$ (7 pont)   Megoldás. Az első számjeggyel megegyezhet a 2., a 3., illetve a 4. jegy, ezért háromféle lehet az adott tulajdonságú szám: $\overline{xxyy}$, $\overline{xyxy}$ és $\overline{xyyx}$ alakú. Ezekben $x$ értéke nem lehet 0, ezért 9-féle lehet. $y$ lehet 0, de $y\ne x$, ezért $y$ is 9-féle lehet, tehát mindegyik típusból 81, összesen 243 megfelelő szám van. $b)$ Egy négyjegyű szám akkor és csak akkor osztható 4-gyel, ha az utolsó két jegyből álló szám osztható 4-gyel. Az $\overline{xxyy}$ típusú számok 00-ra, 44-re vagy 88-ra végződhetnek. A 00-ra végződők előtt 9 féle $x$ jegy, a 44-re vagy 88-ra végződők előtt 8-8 féle $x$ állhat, tehát összesen 25 megfelelő szám van. $\overline{xyxy}$ akkor és csak akkor osztható 4-gyel, ha $\overline{xy}$ osztható 4-gyel, és $x\ne 0$. 12-től 96-ig összesen 22 néggyel osztható szám van, de ezek közül a 44 és a 88 nem jó, tehát összesen 20 db megfelelő szám van. $\overline{xyyx}$ akkor és csak akkor osztható 4-gyel, ha $\overline{yx}$ osztható 4-gyel, és $x\ne$0. $\overline{yx}$ 04-től 96-ig összesen 24 féle lehet, de ezek közül a 20, 40, 44, 60, 80 és a 88 nem jó, tehát összesen 18 db megfelelő szám van. Tehát annak a valószínűsége, hogy 4-gyel osztható számot kapunk: $\begin{array}{c}{\displaystyle p=\frac{25+20+18}{243}=\frac{63}{243}=\frac{7}{27}\approx 0\mathrm{,}259.}\end{array}$ $c)$ $1+2+3+\text{...}+n=\frac{n\left(n+1\right)}{2}$. Ez akkor lesz négyjegyű, ha $45\le n\le 140$. $\begin{array}{c}{\displaystyle \overline{xyxy}=1000x+100y+10x+y=101\left(10x+y\right)\mathrm{.}}\end{array}$ Az $n\left(n+1\right)=2\cdot 101\left(10x+y\right)$ egyenlet megoldásait keressük, ahol $45\le n\le 140$. A jobb oldal osztható a 101 prímszámmal, ezért $n$ vagy $n+1$ is osztható vele. Az adott intervallumban csak $n=101$, vagy $n+1=101$ lehet. Mindkettő jó megoldást ad. $n=101$ esetén $1+2+3+\text{...}+101=5151$, tehát $x=5$, $y=1$. $n=100$ esetén $1+2+3+\text{...}+100=5050$, tehát $x=5$, $y=0$.