Cím:	Megoldásvázlatok a 2017/2. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Számadó László
Füzet:	2017/március, 142 - 150. oldal	PDF  |  MathML
Hivatkozás(ok):	2017/február: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg az alábbi egyenletrendszereket a rendezett valós számpárok halmazán: $\begin{array}{c}{\displaystyle a){\displaystyle \begin{array}{cc}\hfill {\displaystyle x}& {\displaystyle =10-y\mathrm{,}}\hfill \\ \hfill {\displaystyle y}& {\displaystyle =3\sqrt[]{x};}\hfill \end{array}}b){\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{x+3}{4}-\frac{y-2}{3}}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle \frac{4}{x+3}+\frac{3}{y-2}}& {\displaystyle =\frac{4}{3}\mathrm{.}}\hfill \end{array}}}\end{array}$  (11 pont)   Megoldás. $a)$ A keresett rendezett valós számpárban az $x$ nem negatív valós szám lesz (a négyzetgyök miatt), az $y$ tetszőleges valós szám lehet. A második egyenletből az $y=3\sqrt[]{x}$-et behelyettesítve az első egyenletbe az $x=10-3\sqrt[]{x}$ egyenletet kapjuk. Ez $\sqrt[]{x}$-re másodfokú: ${\left(\sqrt[]{x}\right)}^2+3\sqrt[]{x}-10=0$. Az egyenlet két megoldása: ${\left(\sqrt[]{x}\right)}_1=2$, ${\left(\sqrt[]{x}\right)}_2=-5$. A második eset nem ad valós megoldást. Az első esetből kapjuk, hogy $x=4$. A hozzátartozó $y$ érték: $y=3\sqrt[]{4}=6$. A keresett rendezett számpár: $\left(x;y\right)=\left(4;6\right)$. Ez valóban megfelel a feladat összes feltételének. $b)$ Láthatóan: $x\ne -3$, $y\ne 2$. Legyen: $\frac{x+3}{4}=a$, $\frac{y-2}{3}=b$. Ekkor a következő egyenletrendszert kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle a-b}& {\displaystyle =\mathrm{2,}}\hfill \\ \hfill {\displaystyle \frac{1}{a}+\frac{1}{b}}& {\displaystyle =\frac{4}{3}\mathrm{.}}\hfill \end{array}}$ Az első egyenletből az $a=\left(b+2\right)$-t behelyettesítjük a második egyenletbe: $\begin{array}{c}{\displaystyle \frac{1}{b+2}+\frac{1}{b}=\frac{4}{3}\mathrm{.}}\end{array}$ Beszorzunk a $3b\left(b+2\right)$ közös nevezővel, majd az alakítások után másodfokú egyenletet kapunk: $2b^2+b-3=0$. A két gyök: $b_1=-\frac{3}{2}$, $b_2=1$. Az ezekhez tartozó $a$ értékek: $a_1=\frac{1}{2}$, $a_2=3$. Ezek alapján a keresett $\left(x;y\right)$ rendezett valós számpárok: $\left(-1;-\frac{5}{2}\right)$, $\left(9;5\right)$. A feladat feltételeinek mindkét pár megfelel.   2. A Fővárosi Nagycirkusz Dima karácsonya című előadása egy kisfiú álmáról szól. $a)$ Az első felvonásban nyolc műsorszám látható. Dima álmát tegyük változatossá, és legyen minden előadáson eltérő ezeknek a műsorszámoknak a sorrendje. Mennyi ideig játszhatnák így ezt az előadást, ha egy héten nyolcszor láthatja a közönség? $b)$ Az egyensúlyozó művész nyolc geometriai formát tesz egymásra, és ezeknek a tetejére állva zsonglőrködik. Van három darab egyforma álló hengere, két darab egyforma fekvő hengere és három darab egyforma kettőskúpja. Hányféleképpen rakhatja ezeket egymásra? $c)$ Az egyik műsorszámban öt oroszlán szerepel. A jelenet második felében már csak három oroszlán marad a porondon, és ez bármelyik három lehet. Hányféleképpen hagyhatják el az oroszlánok a jelenet végén a porondot? $d)$ Az elefánt számára négy sorszámozott kosárban tíz egyforma almát helyeznek el, amit a műsorszám alatt jutalomként megkap az elefánt. Hányféleképpen lehet az almákat elhelyezni a négy kosárban?  (12 pont)   Megoldás. $a)$ A nyolc műsorszám permutációjáról van szó, ezek száma: $P_8=8!=40320$. Mivel egy évben 52-szer 8 előadás van, ezért a 40 320 és a 416 hányadosát kell vennünk, ami egy tizedesre kerekítve 96,9. Vagyis közel 97 évig játszhatnák ezt az előadást. $b)$ Most nyolc geometriai forma permutációinak számát kell meghatároznunk, de a szöveg alapján látjuk, hogy vannak közöttük azonosak. Ezért ismétléses permutációról van szó. Ezek száma: $\begin{array}{c}{\displaystyle P_8^{3;2;3}=\frac{8!}{3!\cdot 2!\cdot 3!}=\frac{40320}{6\cdot 2\cdot 6}=560.}\end{array}$ Vagyis 560-féleképpen adhatja elő ezt a műsorszámot az egyensúlyozó. $c)$ Bármelyik három oroszlán bent maradhat a szám végére, és ezek valamilyen sorrendben elhagyják a porondot. Vagyis az öt oroszlán harmadosztályú variációiról van szó. Ezek száma: $V_5^3=5\cdot 4\cdot 3=60$. Vagyis 60 különböző eset lehetséges. $d)$ Jelöljük az almákat karikákkal, a négy kosár között pedig képzeljünk el egy-egy függőleges vonalat. Vagyis a $◯◯◯\mid ◯◯\mid \mid ◯◯◯◯◯$ jelsorozat azt jelenti, hogy az első kosárban 3 db, a másodikban 2 db alma található, a harmadik kosár most üres, a negyedikben pedig 5 db alma van. Meggondolható, hogy az így készített jelsorozatok és a kosárba rakott almák esetei kölcsönösen egyértelműen egymáshoz rendelhetők. Számoljuk össze a jelsorozatok számát. Sorba kell raknunk 10 egyforma karikát, és 3 egyforma függőleges vonalat. Ezek száma: $\begin{array}{c}{\displaystyle P_{13}^{10;3}=\frac{13!}{10!\cdot 3!}=\frac{11\cdot 12\cdot 13}{1\cdot 2\cdot 3}=286.}\end{array}$ Vagyis 286-féleképpen osztható szét a tíz alma a négy kosárba.   Megjegyzés. Pontosan 13 jelet kell sorba raknunk, és csak 3 helyre kerül függőleges vonal, a többi karika. Annyi eset lehetséges, ahányféleképpen a 13 hely közül kiválaszthatjuk azt a hármat, ahová a függőleges vonalakat tesszük. Ezek száma: $C_{13}^3=\left(\genfrac{}{}{0ex}{}{13}{3}\right)=286$. Ha valaki ismeri az ismétléses kombinációk számát meghatározó képletet, akkor azzal azonnal megkapja a helyes végeredményt: $\left(\genfrac{}{}{0ex}{}{4+10-1}{10}\right)=286$.   3. A matematika dolgozatban egy $n$ pontú teljes gráf éleinek számát kellett meghatározni. Ügyet Lenke az $n$ oldalú sokszög átlóinak számára vonatkozó képletet használta, és ráadásul az így kapott szám két utolsó számjegyét véletlenül felcserélte. Ügyetlenkedéseinek ellenére helyes végeredményt kapott. Hány pontú gráf szerepelt a dolgozatban?  (14 pont)   Megoldás. Gondoljuk meg, hogy a két szám különbsége a sokszög csúcsainak számát adja. Ezt a megállapításunkat a két képlet ismeretében algebrai átalakításokkal is megmutathatjuk: $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\frac{n\left(n-3\right)}{2}=\frac{n^2-n-n^2+3n}{2}=n\mathrm{.}}\end{array}$ Tudjuk, hogy az élek száma és az átlók száma legalább kétjegyű, különböző egész számok, hiszen a kisebbikben a két utolsó számjegyet Lenke fel tudta cserélni. Belátjuk, hogy két ilyen szám különbsége 9-cel osztható. Legyen $\frac{n\left(n-1\right)}{2}=100a+10b+c$, ekkor $\frac{n\left(n-3\right)}{2}=100a+10c+b$, ahol $a$ természetes számot, $b$ és $c$ számjegyeket jelöl, továbbá $b>c$. Ekkor $\begin{array}{c}{\displaystyle \frac{n\left(n-1\right)}{2}-\frac{n\left(n-3\right)}{2}=n=10\left(b-c\right)+c-b=9\left(b-c\right)\mathrm{.}}\end{array}$ A $b-c$ értéke a feltételek figyelembevételével: $\mathrm{1,2,3,}\text{...}\mathrm{,9}$, vagyis $n$-re kilenc darab 9-cel osztható szám lehetősége adódik. Ezeket a lehetséges eseteket táblázatban rögzítjük:   ${\displaystyle \begin{array}{|cccccccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math>}}\hfill & \hfill {\displaystyle \text{9}}\hfill & \hfill {\displaystyle \text{18}}\hfill & \hfill {\displaystyle \text{27}}\hfill & \hfill {\displaystyle \text{36}}\hfill & \hfill {\displaystyle \text{45}}\hfill & \hfill {\displaystyle \text{54}}\hfill & \hfill {\displaystyle \text{63}}\hfill & \hfill {\displaystyle \text{72}}\hfill & \hfill {\displaystyle \text{81}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>n</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi><mo stretchy="false">-</mo><mn>3</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{27}}\hfill & \hfill {\displaystyle \text{135}}\hfill & \hfill {\displaystyle \text{324}}\hfill & \hfill {\displaystyle \text{594}}\hfill & \hfill {\displaystyle \text{945}}\hfill & \hfill {\displaystyle \text{1377}}\hfill & \hfill {\displaystyle \text{1890}}\hfill & \hfill {\displaystyle \text{2484}}\hfill & \hfill {\displaystyle \text{3159}}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mfrac><mrow><mi>n</mi><mrow><mo fence="true" stretchy="true">(</mo><mrow><mi>n</mi><mo stretchy="false">-</mo><mn>1</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></mrow><mrow><mn>2</mn></mrow></mfrac></mrow></math>}}\hfill & \hfill {\displaystyle \text{36}}\hfill & \hfill {\displaystyle \text{153}}\hfill & \hfill {\displaystyle \text{351}}\hfill & \hfill {\displaystyle \text{630}}\hfill & \hfill {\displaystyle \text{990}}\hfill & \hfill {\displaystyle \text{1431}}\hfill & \hfill {\displaystyle \text{1953}}\hfill & \hfill {\displaystyle \text{2556}}\hfill & \hfill {\displaystyle \text{3240}}\hfill \\ \hline\end{array}}$   Az $n$-hez tartozó számpárok közül csak a 135 olyan, hogy a két utolsó számjegy felcserélésével a másik számot kapjuk. Vagyis $n=18$, azaz 18 pontú gráf szerepelt a dolgozatban.   4. Adott a koordinátarendszerben az $e:x-2y=0$ egyenes és az $A\left(14;2\right)$ pont. Tudjuk, hogy $AC=BC$, ahol $C$ illeszkedik az $e$ egyenes első negyedbe eső részére, $B$ illeszkedik az $x$ tengelyre, és $CB$ párhuzamos az $y$ tengellyel. Adjuk meg a $C$ és $B$ pontok koordinátáit.  (14 pont)   Megoldás. Legyen $C\left(2c;c\right)$, ahol $c$ egy pozitív számot jelöl, ekkor $C$ illeszkedik az $e$ egyenesre. A feladat feltételei szerint ekkor $B\left(2c;0\right)$ lesz. Fejezzük ki a koordináták segítségével az $AC$ és $BC$ szakaszok hosszát. Az $AC$ szakasz hosszát megkaphatjuk a távolságképlet felhasználásával: $\begin{array}{c}{\displaystyle AC=\sqrt[]{{\left(14-2c\right)}^2+{\left(2-c\right)}^2}=\sqrt[]{196-56c+4c^2+4-4c+c^2}=\sqrt[]{5c^2-60c+200}\mathrm{.}}\end{array}$ A $BC$ szakasz párhuzamos az $y$ tengellyel, hossza: $BC=c$. Tudjuk, hogy $AC=BC$ (azaz ${AC}^2={BC}^2)$, ezért $5c^2-60c+200=c^2$. Rendezés és 4-gyel való osztás után a $c^2-15c+50=0$ másodfokú egyenletet kell megoldanunk. A gyökök és együtthatók közötti összefüggéssel is jól látható: $c_1=5$, $c_2=10$. Vagyis két megoldás van. A keresett pontok koordinátái: ${\displaystyle \begin{array}{ccc}{\displaystyle \text{<span style="font-style: italic;">I. eset:</span>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>B</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>10</mn><mi>;</mi><mn>0</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>C</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>10</mn><mi>;</mi><mn>5</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>,}}\hfill \\ {\displaystyle \text{<span style="font-style: italic;">II. eset:</span>}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>B</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>20</mn><mi>;</mi><mn>0</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>,}}\hfill & {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>C</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow><mrow><mo fence="true" stretchy="true">(</mo><mrow><mn>20</mn><mi>;</mi><mn>10</mn></mrow><mo fence="true" stretchy="true">)</mo></mrow></math>.}}\hfill \end{array}}$   II. rész     5. Egy feldolgozóüzem adott térfogatú, henger alakú konzervdobozokat szeretne gyártatni. A dobozoknak a palástja és csak az egyik fedőlapja lesz címkével borítva. Milyen alakú hengert kell terveztetniük, hogy a címkézendő felület a lehető legkisebb legyen? Adjuk meg a henger magassága és a sugara közötti kapcsolatot.  (16 pont)   Megoldás. A henger térfogatképletéből kifejezzük a henger magasságát: $m=\frac{V}{r^2\pi }$. Ekkor a címkézendő felület nagysága: $\begin{array}{c}{\displaystyle P+T=2r\pi \cdot m+r^2\pi =2r\pi \cdot \frac{V}{r^2\pi }+r^2\pi =\frac{2V}{r}+r^2\pi \mathrm{.}}\end{array}$ Ez a következő alakban is írható: $\begin{array}{c}{\displaystyle P+T=\frac{2V}{r}+r^2\pi =\frac{V}{r}+\frac{V}{r}+r^2\pi \mathrm{.}}\end{array}$ Alkalmazzuk a számtani és mértani közép közötti egyenlőtlenséget $\frac{V}{r}$, $\frac{V}{r}$ és $r^2\pi$ értékekre: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{\frac{V}{r}+\frac{V}{r}+r^2\pi }{3}}& {\displaystyle \ge \sqrt[3]{\frac{V}{r}\cdot \frac{V}{r}\cdot r^2\pi }\mathrm{,}}\hfill \\ \hfill {\displaystyle \frac{V}{r}+\frac{V}{r}+r^2\pi }& {\displaystyle \ge 3\cdot \sqrt[3]{V^2\cdot \pi }\mathrm{.}}\hfill \end{array}}$ Az egyenlőtlenség jobb oldalán konstans szerepel, hiszen $V$ értéke adott volt. A bal oldalon álló háromtagú összeg akkor lesz minimális, ha pontosan ezzel a konstanssal egyenlő. Egyenlőség pedig akkor és csak akkor van, ha a három tag értéke egyenlő. Vagyis: $\frac{V}{r}=r^2\pi$. Ebből kapjuk, hogy $r=\sqrt[3]{\frac{V}{\pi }}$. Visszahelyettesítéssel kifejezhető a henger magassága is: $\begin{array}{c}{\displaystyle m=\frac{V}{{\left(\sqrt[3]{\frac{V}{\pi }}\right)}^2\cdot \pi }=\sqrt[3]{\frac{V}{\pi }}\mathrm{.}}\end{array}$ Azt kaptuk, hogy $m=r$. Vagyis olyan hengerekre lesz szükség, amelyben a magasság egyenlő az alapkör sugarával, akkor lesz a címkézendő felület adott térfogat mellett minimális.   Megjegyzés. A megoldás során kiderült, hogy az $f\left(r\right)=\frac{2V}{r}+r^2\pi$ hozzárendelésű függvény minimumhelyét kell megkeresnünk. Ezt deriválással is megkaphatjuk: $\begin{array}{c}{\displaystyle f\text{'}\left(r\right)=\left(2V\cdot r^{-1}\right)\text{'}+\left(r^2\pi \right)\text{'}=2V\cdot \left(-r^{-2}\right)+2r\pi =-\frac{2V}{r^2}+2r\pi \mathrm{.}}\end{array}$ Szélsőérték a derivált zérushelyeinél lehet, ezért szükségünk van az $r\pi -\frac{V}{r^2}=0$ egyenlet megoldására. Az egyenlet egyedüli megoldása az $r=\sqrt[3]{\frac{V}{\pi }}$, ami azt jelenti, hogy az $f\left(r\right)$ függvénynek csak ezen a helyen lehet szélsőértéke. Megvizsgálható, hogy a derivált ezen a helyen előjelet vált negatívból pozitívra, ezért itt minimumhelye van a vizsgált függvénynek. Innen ugyanahhoz a megállapításhoz jutunk, mint az előző megoldásban.   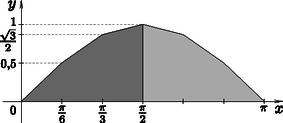6. $a)$ Határozzuk meg a $\left[0;\pi \right]$-n értelmezett $f\left(x\right)=\text{sin}x$ hozzárendeléssel megadott függvény görbéje és az $x$ tengely által határolt síkidom területének közelítő értékét. A számoláshoz használjuk azt a hétszöget, amelynek csúcsai a függvény görbéjén találhatók a $0$, $\frac{\pi }{6}$, $\frac{\pi }{3}$, $\pi$, $\frac{2\pi }{3}$, $\frac{5\pi }{6}$ és $\pi$ helyeken. $b)$ Határozzuk meg a $\left[0;\pi \right]$-n értelmezett $f\left(x\right)=\text{sin}x$ hozzárendeléssel megadott függvény görbéje és az $x$ tengely által határolt síkidom területét.  (16 pont)   Megoldás. $a)$ Vegyük fel az $\left(x;f\left(x\right)\right)$ koordinátájú pontokat, ha $x$ értéke 0, $\frac{\pi }{6}$, $\frac{\pi }{3}$, $\pi$, $\frac{2\pi }{3}$, $\frac{5\pi }{6}$, $\pi$. Ezeket a pontokat összekötve az ábrán látható hétszöget kapjuk.     Mivel ez a síkidom szimmetrikus, ezért elegendő a sötétebb színnel színezett rész területének meghatározása, mert ez az eredeti hétszög területének éppen a fele. Vágjuk ezt az ötszöget az $y$ tengellyel párhuzamos vágásokkal egy háromszögre és két trapézra. A megfelelő adatokat az ábráról leolvashatjuk, és ezek segítségével a kérdéses síkidom területének közelítő értékét meghatározhatjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{T}{2}}& {\displaystyle =\frac{\frac{1}{2}\cdot \frac{\pi }{6}}{2}+\frac{\left(\frac{1}{2}+\frac{\sqrt[]{3}}{2}\right)\cdot \frac{\pi }{6}}{2}+\frac{\left(\frac{\sqrt[]{3}}{2}+1\right)\cdot \frac{\pi }{6}}{2}\mathrm{,}\text{azaz}}\hfill \\ \hfill {\displaystyle T}& {\displaystyle =\frac{\pi }{6}\left(2+\sqrt[]{3}\right)\approx 1\mathrm{,}954\text{(területegység).}}\hfill \end{array}}$ $b)$ A megadott intervallumon a görbe alatti területet kell meghatároznunk. Ezt határozott integrállal kaphatjuk meg: $\begin{array}{c}{\displaystyle T=\underset{0}{\overset{\pi }{\int }}\text{sin}xdx={\left[-\text{cos}x\right]}_0^{\pi }=-\text{cos}\pi -\left(-\text{cos}0\right)=1-\left(-1\right)=2.}\end{array}$ Vagyis a kérdéses terület pontosan 2 területegység.   7. Az Öltönyüzletben minden héten kitalálnak egy új akciót, amivel a vásárlók kedvében szeretnének járni. $a)$ Az egyik héten meghirdették, hogy a 4990 Ft-os ingek közül az elsőt 990 Ft-ért vásárolhatjuk meg, és ezen felül még annyi inget vehetünk 990 Ft-ért, ahányat teljes áron. Beáta, az üzlet öltözködési tanácsadója szerint ezek jó minőségű ingek, ezért László egynél többet szeretne választani magának. Hány darabot vegyen, ha átlagosan a legkevesebbet szeretne fizetni egy ingért? $b)$ Egy másik alkalommal az üzlet vezetősége két akció közül nem tudott választani, ezért a vásárlóikat kérdezték meg, hogy ők melyiket szeretnék. A beérkezett szavazatok alapján a következő két ajánlat között fognak dönteni: Egyik lehetőség: Aki két terméket vásárol, az olcsóbbat fél áron kapja. Másik lehetőség: Aki három terméket vásárol, a legolcsóbbat ingyen kapja. László a következő termékeket szeretné megvásárolni: öltöny 39 990 Ft, kabát 27 990 Ft, duplagalléros ing 6490 Ft, bőr öv 3990 Ft, selyem nyakkendő 2990 Ft, sportos kordzakó 29 990 Ft. Adjuk meg a különböző párosítások alapján a lehetséges fizetendő összegeket az első lehetőség szerint. $c)$ Az első akcióra $2103$, a másodikra $1542$ szavazat érkezett. Kedvező ez Lászlónak? Mekkora és milyen irányú eltérést jelent ez az általa választott termékek kifizetésekor? (Azt feltételezzük, hogy László mindkét lehetőségnél a számára legjobb csoportosításban fizetett volna.)  (16 pont)   Megoldás. $a)$ Ha László $2n$ darabszámú inget vásárolna ($n$ tetszőleges pozitív egész szám), akkor $n$ darab inget venne 990 Ft-os, és $n$ darabot 4 990 Ft-os egységáron. Ekkor az átlagár: $\begin{array}{c}{\displaystyle \frac{990\cdot n+4990\cdot n}{2n}=\frac{990+4990}{2}=2990\text{(Ft). }}\end{array}$ Ha $2n+1$ darabszámú inget vásárolna ($n$ tetszőleges pozitív egész szám), akkor $n+1$ darab inget venne 990 Ft-os, és $n$ darabot 4 990 Ft-os egységáron. Ekkor az átlagár: $\begin{array}{c}{\displaystyle a_n=\frac{990\cdot \left(n+1\right)+4990\cdot n}{2n+1}=\frac{5980n+990}{2n+1}\text{(Ft). }}\end{array}$ Az $a_n$ általános taggal adott sorozat tagjai megadják a $2n+1$ darabszámú ing vásárlása esetén az átlagárat. Mivel például $a_1=\frac{5980\cdot 1+990}{2+1}\approx 2325$ (Ft), ezért 3 ing vásárlása esetén 2 325 Ft az átlagár. Megmutatjuk, hogy az $\left\{a_n\right\}$ sorozat szigorúan monoton növekedő, azaz minden $n$ pozitív egész szám esetén $a_n<a_{n+1}$. Ehhez vizsgáljuk meg az $\begin{array}{c}{\displaystyle \frac{5980n+990}{2n+1}<\frac{5980\left(n+1\right)+990}{2\left(n+1\right)+1}}\end{array}$ egyenlőtlenséget. Ha a pozitív közös nevezővel szorozzuk az egyenlőtlenséget, és rendezzük, akkor a nyilvánvaló $2970<6970$ egyenlőtlenséghez jutunk. Vagyis valóban szigorúan monoton növekedő a sorozat. Ezek alapján látjuk, hogy $a_1$ esetén kapjuk a legkisebb átlagárat, azaz 3 darab ing vásárlása esetén. Ez a 2 325 Ft a páros darabszámú vásárlás esetén kapott 2 990 Ft-os átlagárnál is kisebb. Vagyis László 3 darabot vegyen, ha átlagosan a legkevesebbet szeretné fizetni egy ingért.   Megjegyzés. Mivel $\begin{array}{c}{\displaystyle \underset{n\to \infty }{\overset{}{\text{lim}}}\frac{5980n+990}{2n+1}=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{5980+\frac{990}{n}}{2+\frac{1}{n}}=2\mathrm{990,}}\end{array}$ ezért nagyon sok, de páratlan darabszámú ing vásárlása esetén látható, hogy az átlagár közelít a páros darabszámú vásárlásnál kapott átlagárhoz. $b)$ Gondoljuk meg, hogy a hat termék közül melyik három kerülhet a féláras termékek közé. Rakjuk az árak alapján csökkenő sorrendbe a megvásárlásra szánt dolgokat:   ${\displaystyle \begin{array}{ccc}{\displaystyle \text{ 1.}}\hfill & {\displaystyle \text{öltöny:}}\hfill & \hfill {\displaystyle \text{39 990 Ft;}}\\ {\displaystyle \text{ 2.}}\hfill & {\displaystyle \text{sportos kordzakó:}}\hfill & \hfill {\displaystyle \text{29 990 Ft;}}\\ {\displaystyle \text{ 3.}}\hfill & {\displaystyle \text{kabát:}}\hfill & \hfill {\displaystyle \text{27 990 Ft;}}\\ {\displaystyle \text{ 4.}}\hfill & {\displaystyle \text{duplagalléros ing:}}\hfill & \hfill {\displaystyle \text{6 490 Ft;}}\\ {\displaystyle \text{ 5.}}\hfill & {\displaystyle \text{bőröv:}}\hfill & \hfill {\displaystyle \text{3 990 Ft;}}\\ {\displaystyle \text{ 6.}}\hfill & {\displaystyle \text{selyem nyakkendő:}}\hfill & \hfill {\displaystyle \text{2 990 Ft.}}\end{array}}$   A legdrágább soha nem lehet féláras ebben az akcióban, a legolcsóbb pedig mindig az lesz. Az összes esetet könnyen fel tudjuk sorolni a sorszámok segítségével, és mellé írjuk a három termék árának felét, amennyit ekkor megspórolunk a teljes árból:   ${\displaystyle \begin{array}{cc}{\displaystyle \text{ 4, 5, 6}}\hfill & \hfill {\displaystyle \text{6 735 Ft;}}\\ {\displaystyle \text{ 3, 5, 6}}\hfill & \hfill {\displaystyle \text{17 485 Ft;}}\\ {\displaystyle \text{ 2, 5, 6}}\hfill & \hfill {\displaystyle \text{18 735 Ft;}}\\ {\displaystyle \text{ 3, 4, 6}}\hfill & \hfill {\displaystyle \text{18 485 Ft;}}\\ {\displaystyle \text{ 2, 4, 6}}\hfill & \hfill {\displaystyle \text{19 735 Ft.}}\end{array}}$   A hat termék teljes ára 111 440 Ft lenne. Ha ezt csökkentjük az előbb felsorolt lehetséges engedményekkel, akkor megkapjuk a lehetséges fizetendő összegeket: 104 705 Ft, 93 955 Ft, 92 705 Ft, 92 955 Ft, 91 705 Ft. $c)$ A szavazatok alapján az első akciót hirdette meg az Öltönyüzlet. Ebben az esetben úgy érdemes párosítani a termékeket, hogy a második, a negyedik és a hatodik legyen a féláras. Ekkor a fizetendő összeg $111440-19735=91705$ Ft lesz. Ha a másik akciót választotta volna a többség, akkor bármilyen csoportosítás esetén a selyem nyakkendő ingyenes lenne. Egyébként 2 990 Ft az ára. Ha a legjobban szeretnénk járni, akkor ki kell választanunk a legdrágábbat, amelyik szerepelhet ingyenesként. Ez természetesen a 27 990 Ft-os kabát. Ekkor a fizetendő összeg: $111440-2990-27990=80460$ Ft. László számára ez az akció kedvezőbb lett volna, hiszen a végösszeg 11 245 Ft-tal kisebb, mint a másik esetben.   8. Tudjuk, hogy az első $n$ darab négyzetszám összegét az $\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ képlet adja, és az $n$-edik négyzetszám az $n^2$. Tudjuk, hogy az első $n$ darab háromszögszám összegét az $\frac{n\left(n+1\right)\left(n+2\right)}{6}$ képlet adja, és az $n$-edik háromszögszám az $\frac{n\left(n+1\right)}{2}$. $a)$ Igazoljuk, hogy az $n$-edik és az $\left(n+1\right)$-edik háromszögszám összege négyzetszám. $b)$ Igazoljuk, hogy ha az $n$-edik háromszögszámhoz hozzáadjuk az $\left(n+1\right)$-edik háromszorosát, akkor ismét háromszögszámot kapunk. 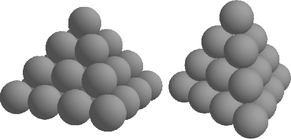A zöldséges a mandarinokból négyzet alapú és háromszög alapú, magas piramist épített. (Az ábra mutat egy-egy négyrétegű ilyen piramist.) $c)$ Emőke a négyzet alapú piramis tetejéről megvesz néhány rétegnyi mandarint. Egy heti adagot szeretne vásárolni úgy, hogy minden napra ugyanannyi mandarin jusson. Adjuk meg a darabszámoknak azt a sorozatát, ahány réteg mandarint Emőke megvásárolhat.     $d)$ Ha a megvásárolt mandarinok számát Emőke négyszerezné, akkor kétszer olyan magas háromszög alapú piramist tudna építeni, mint amilyen magas négyzet alapú piramis volt eredetileg. Igazoljuk, hogy ez az észrevétel nem függ attól, hogy a boltban a piramis tetejéről hány réteg mandarint vásárolt meg.  (16 pont)   Megoldás. $a)$ Tudjuk, hogy az $n$-edik háromszögszám: $\frac{n\left(n+1\right)}{2}$, ezért az $\left(n+1\right)$-edik: $\frac{\left(n+1\right)\left(n+2\right)}{2}$. A két szám összege: $\begin{array}{c}{\displaystyle \frac{n\left(n+1\right)}{2}+\frac{\left(n+1\right)\left(n+2\right)}{2}=\frac{\left(n+1\right)\left(n+n+2\right)}{2}=\frac{\left(n+1\right)\left(2n+2\right)}{2}={\left(n+1\right)}^2\mathrm{.}}\end{array}$ Valóban négyzetszámot kaptunk (az $\left(n+1\right)$-ediket). $b)$ Felhasználjuk az $n$-edik és az $\left(n+1\right)$-edik háromszögszámot előállító képletet: $\begin{array}{c}{\displaystyle \frac{n\left(n+1\right)}{2}+3\cdot \frac{\left(n+1\right)\left(n+2\right)}{2}=\frac{\left(n+1\right)\left(4n+6\right)}{2}=\frac{\left(2n+2\right)\left(2n+3\right)}{2}\mathrm{.}}\end{array}$ Az így kapott képlet mutatja, hogy háromszögszámot kaptunk. (A képletből az is kiolvasható, hogy ez a $\left(2n+2\right)$-edik.) $c)$ A megvásárolható mandarinok száma: $\begin{array}{c}{\displaystyle 1+4+\text{...}+n^2=\frac{n\left(n+1\right)\left(2n+1\right)}{6}\mathrm{.}}\end{array}$ Az így kapott darabszámnak 7-tel oszthatónak kell lennie, hiszen csak ekkor lehet a hét minden napján ugyanannyit elfogyasztani. A négyzetszámok összege egész szám. (Vagyis abban biztosak lehetünk, hogy a számláló osztható 6-tal). A számlálóban lévő tényezők valamelyikének 7-tel oszthatónak kell lenni. Ezek alapján három eset van: I. az $n$ osztható 7-tel; II. az $n$ 7-tel osztva 6 maradékot ad; III. az $n$ 7-tel osztva 3 maradékot ad. Vagyis a megvásárolható rétegek darabszámára vonatkozó sorozat: 3; 6; 7; 10; 13; 14; $\text{...}$; $7k+3$; $7k+6$; $7k+7$; $\text{...}$ (ahol $k$ természetes szám). $d)$ Ha Emőke $\frac{n\left(n+1\right)\left(2n+1\right)}{6}$ darab mandarint vásárolt (azaz az $n$-edik négyzetszámig végezte el az összegzést), akkor az állítás szerint ennek a darabszámnak a négyszereséből kétszer olyan magas háromszög alapú piramist tudna építeni (azaz a $2n$-edik háromszögszámig tudná az összegzést elvégezni). A $2n$-edik háromszögszámig az összeg: $\frac{2n\left(2n+1\right)\left(2n+2\right)}{6}$. Az elmondottak alapján azt kell megmutatnunk, hogy a következő összefüggés egy azonosság: $\begin{array}{c}{\displaystyle 4\cdot \frac{n\left(n+1\right)\left(2n+1\right)}{6}=\frac{2n\left(2n+1\right)\left(2n+2\right)}{6}\mathrm{.}}\end{array}$ Ez azonnal látható a 4-gyel történő beszorzás után: $\begin{array}{c}{\displaystyle \frac{2n\left(2n+2\right)\left(2n+1\right)}{6}=\frac{2n\left(2n+1\right)\left(2n+2\right)}{6}\mathrm{.}}\end{array}$   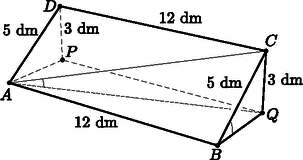9. $a)$ Az 5 dm-szer 12 dm-es téglalap hosszabb oldala a vízszintes síkra illeszkedik, két csúcsa pedig 3 dm magasan van a sík fölött. Ezen a téglalapon egy hangya mászik a hosszabb oldalra merőlegesen felfelé. Mennyivel lenne kisebb az útvonalának a vízszintessel bezárt hajlásszöge, ha a téglalap átlóján mászna felfelé? $b)$ Igazoljuk, hogy ha $a$, $b$ és $c$ egy háromszög oldalainak a hossza, $\alpha$, $\beta$ és $\gamma$ pedig a megfelelő szögeinek a nagysága, akkor: $\begin{array}{c}{\displaystyle b^{3}c\cdot \text{cos}\alpha +c^{3}a\cdot \text{cos}\beta +a^{3}b\cdot \text{cos}\gamma =c^{3}b\cdot \text{cos}\alpha +a^{3}c\cdot \text{cos}\beta +b^{3}a\cdot \text{cos}\gamma \mathrm{.}}\end{array}$  (16 pont)   Megoldás. $a)$ Az ábrán az $ABCD$ téglalap $BC$ oldalán haladhat felfelé a hangya. Vagyis ebben az esetben a $CBQ$ szög a hajlásszög. A feladatban szereplő másik útvonal lehet az $AC$. Ebben az esetben $CAQ$ hajlásszögről van szó. Mindkettő meghatározható egy-egy derékszögű háromszögből.     A $CBQ$ derékszögű háromszögben: $\text{sin}CBQ\sphericalangle =\frac{3}{5}$, azaz $CBQ\sphericalangle \approx 36\mathrm{,}{9}^{\circ }$. Az $ABC$ derékszögű háromszögben a Pitagorasz-tétellel kapható: $AC=\sqrt[]{{12}^2+5^2}=13$. A $CAQ$ derékszögű háromszögben: $\text{sin}CAQ\sphericalangle =\frac{3}{13}$, azaz $CAQ\sphericalangle \approx 13\mathrm{,}{3}^{\circ }$. A két hajlásszög eltérése: $36\mathrm{,}{9}^{\circ }-13\mathrm{,}{3}^{\circ }=23\mathrm{,}{6}^{\circ }$. A másik útvonal hajlásszöge kb. $23\mathrm{,}{6}^{\circ }$-kal lenne kisebb. $b)$ Alkalmazzuk a koszinusztételt olyan módon, hogy mindhárom szög koszinuszát megadjuk az oldalhosszak segítségével: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{b^2+c^2-a^2}{2bc}\mathrm{,}\text{cos}\beta =\frac{a^2+c^2-b^2}{2ac}\mathrm{,}\text{cos}\gamma =\frac{a^2+b^2-c^2}{2ab}\mathrm{.}}\end{array}$ Ezeket írjuk be az igazolandó összefüggésbe, de előtte rendezzük a következő alakra: $\begin{array}{c}{\displaystyle \left(b^{3}c-c^{3}b\right)\cdot \text{cos}\alpha +\left(c^{3}a-a^{3}c\right)\cdot \text{cos}\beta +\left(a^{3}b-b^{3}a\right)\cdot \text{cos}\gamma =0.}\end{array}$ Alakítsuk a bal oldalt a behelyettesítés után: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \left(b^{3}c-c^{3}b\right)\cdot \frac{b^2+c^2-a^2}{2bc}+\left(c^{3}a-a^{3}c\right)\cdot \frac{a^2+c^2-b^2}{2ac}+\left(a^{3}b-b^{3}a\right)\cdot \frac{a^2+b^2-c^2}{2ab}=}\hfill \\ \hfill {\displaystyle =\left(b^2-c^2\right)\cdot \frac{b^2+c^2-a^2}{2}+\left(c^2-a^2\right)\cdot \frac{a^2+c^2-b^2}{2}+\left(a^2-b^2\right)\cdot \frac{a^2+b^2-c^2}{2}\mathrm{.}}\hfill \end{array}}$ A beszorzás elvégzése után minden tag kiesik, vagyis egyenlő lesz nullával. Ezzel az állítást igazoltuk.