¹
Kivonat. Adott a síkon vagy a térben egy véges ponthalmaz. Célunk olyan hálózat keresése, amely összeköti a halmaz pontjait és a legrövidebb összhosszal rendelkezik. A fő eredményben olyan feltételeket adunk meg, amelyekkel egy legrövidebb hálózat szükségképpen rendelkezik. A fizikai elveken alapuló tárgyalást néhány alkalmazással és történeti adalékkal egészítjük ki.

 

Bizonyítás. Tekintsük az $AC$ oldalegyenes által meghatározott azon nyílt félsíkot, mely nem tartalmazza a $B$ csúcsot. E félsíkot a másik két oldal egyenese három (nem korlátos) tartományra bontja. Tegyük fel, hogy $P$ abban a tartományban van, amely a háromszög oldalszakaszával határos. Ekkor a $BP$ szakasz valamely $M$ pontban metszi az $AC$ oldalt, és

$\begin{array}{c}{\displaystyle AP+BP+CP>AC+BP>AC+BM=AM+BM+CM\mathrm{.}}\end{array}$

Tehát $P$ nem lehet megoldása az (F) Fermat-feladatnak. Most tegyük fel, hogy $P$ olyan tartományban van, amely nem oldalszakasszal határos. Föltehető, hogy a $P$-hez legközelebb az $A$ csúcs helyezkedik el. Mivel $BAC\sphericalangle <\pi$, ezért a $PAB$ és $PAC$ háromszögek egyikében az $A$ tompaszögű csúcs. Föltehető, hogy ez épp a $PAC$ háromszög. Ekkor $AC<PC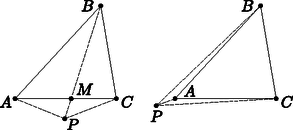$, s így

$\begin{array}{c}{\displaystyle AP+BP+CP>AP+BP+CA>AB+AC\mathrm{.}}\end{array}$

 

 

Ezek szerint $P$ most sem megoldása az (F) Fermat-feladatnak. Megismételve ugyanezt az érvelést a háromszög valamennyi oldalegyenesére, a bizonyítandó állítást kapjuk.  $\square$

 

2. lemma. (Kötött eset.) Ha $ABC$ olyan háromszög, melynek szögei a $2\pi /3$ értéknél kisebbek, akkor az (F) Fermat-feladat megoldása a háromszög izogonális pontja, vagyis az a pont, melyből az oldalak azonos szögben látszanak.

 

Bizonyítás. Legyen ugyanis $P$ tetszőleges síkbeli pont. Az előző lemma miatt föltehető, hogy $P$ az $ABC$ háromszöghöz tartozik. Forgassuk el a $BPC=B{P}_1{C}_1$ háromszöget kifelé $\pi /3$ szögben. Legyen $B{P}_2{C}_2$ az így kapott háromszög. Ekkor $B{P}_1{P}_2$ szabályos háromszög, ezért $P_1{P}_2=B{P}_1$ és $P_1{C}_1=P_2{C}_2$. Tehát

$\begin{array}{c}{\displaystyle AP+BP+CP=A{P}_1+B{P}_1+C_1{P}_1=A{P}_1+P_1{P}_2+P_2{C}_2\mathrm{.}}\end{array}$

Nyilván az $A{P}_1{P}_2{C}_2$ töröttvonal hossza legalább akkora, mint az $A{C}_2$ szakasz hossza. Ennek köszönhetően $P$ csak akkor szolgáltathat minimumot, ha $A$, $P_1$, $P_2$, $C_2$ közös egyenesre illeszkednek. Ez azt jelenti, hogy $APC\sphericalangle =2\pi /3$ szükségképpen fönnáll.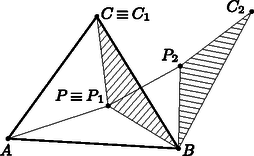

 

 

Hasonló gondolatmenetet követve, $P$ csak úgy lehet megoldása az (F) Fermat-feladatnak, ha az ott összefutó, csúcsokból induló élek $2\pi /3$ szögben találkoznak. Vagyis, ha $P$ a háromszög izogonális pontja.
Az érvelésből az is következik, hogy a háromszög bármely pontjából a csúcsokba húzott szakaszok összhossza legalább akkora, mint az izogonális pontból a csúcsokba húzott szakaszok összhossza. Tehát a szóban forgó minimum feladatnak létezik megoldása, és azt az izogonális pont választásával nyerjük.  $\square$

 

3. lemma. (Lebegő eset.) Ha $ABC$ olyan háromszög, melynek van legalább $2\pi /3$ nagyságú szöge, akkor az (F) Fermat-feladat megoldása a háromszög tompaszögű csúcsa.

 

Bizonyítás. Tegyük föl, hogy az $ABC=A{B}_1{C}_1$ háromszögben a $B$ csúcsnál található a szóban forgó szög. Tekintsük a háromszög tetszőleges olyan $P$ pontját, mely nem a $B$ csúcs. Vegyük föl a $C_2$ pontot úgy, hogy $B_1{C}_1=B_1{C}_2$, valamint $A{B}_1{C}_2\sphericalangle =2\pi /3$ teljesüljenek. Az általánosság sérelme nélkül föltehető, hogy $P$ benne van az $A{B}_1{C}_2$ háromszögben; egyébként ugyanis hasonló konstrukciót alkalmazhatunk $C$ helyett az $A$ csúcsra. Végezetül, válasszuk meg a $B_2$ pontot tetszőlegesen a $B_1$-ből induló azon félegyenesen, amely $2\pi /3$ szöget zár be azokkal a félegyenesekkel, melyek $B_1$-ből indulnak és tartalmazzák az $A$, illetve a $C_2$ pontokat.

 

 

Mivel az $A{B}_2{C}_2$ háromszögnek $B_1$ izogonális pontja, ezért a 2. lemma miatt megoldása az $A$, $B_2$, $C_2$ pontokra vonatkozó (F) Fermat-feladatnak. Ily módon

$\begin{array}{c}{\displaystyle A{B}_1+B_2{B}_1+C_2{B}_1<AP+B_{2}P+C_{2}P<AP+B_2{B}_1+B_{1}P+C_{2}P}\end{array}$

adódik, amiből rendezéssel (és a jelölések figyelembe vételével) kapjuk, hogy

$\begin{array}{c}{\displaystyle AB+BC=A{B}_1+B_1{C}_1=A{B}_1+B_1{C}_2<AP+B_{1}P+C_{2}P\mathrm{.}}\end{array}$

Elegendő tehát csupán azt igazolnunk, hogy $C_{2}P<C_{1}P$. Ez azonban következik abból, hogy a $P{C}_1{C}_2$ háromszögben a $C_1$ csúcsnál lévő szög kisebb, mint a $C_2$ csúcsnál lévő szög.  $\square$

 

Megjegyzés. A Torricelli-asztalon a csomópont egészen a tompaszögű csúcsig mozdul el, mert az erők nem tudják kiegyenlíteni egymást.

 

Rövidesen kiderül, hogy a Fermat-feladat messze túlnövi az esettanulmány kategóriáját. A fő eredmény síkbeli változata jelentős részben ezen múlik. A térbeli változathoz azonban szükségünk lesz még egy eredményre.

 

4. lemma. Ha $ABCD$ tetszőleges tetraéder, akkor

$\begin{array}{c}{\displaystyle \underset{}{\overset{}{\text{min}}}\left\{BAC\sphericalangle \mathrm{,}CAD\sphericalangle \mathrm{,}DAB\sphericalangle \right\}<\frac{2\pi }{3}\mathrm{.}}\end{array}$

 

Bizonyítás. Legyenek ${\text{a}}_1$, ${\text{a}}_2$, ${\text{a}}_3$ az $A$ csúcsból rendre a $B$, $C$, $D$ csúcsok irányába mutató egységvektorok, valamint

${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\alpha }_1}& {\displaystyle :=\sphericalangle \left({\text{a}}_2\mathrm{,}{\text{a}}_3\right)=CAD\sphericalangle \mathrm{,}}\hfill \\ \hfill {\displaystyle {\alpha }_2}& {\displaystyle :=\sphericalangle \left({\text{a}}_3\mathrm{,}{\text{a}}_1\right)=DAB\sphericalangle \mathrm{,}}\hfill \\ \hfill {\displaystyle {\alpha }_3}& {\displaystyle :=\sphericalangle \left({\text{a}}_1\mathrm{,}{\text{a}}_2\right)=BAC\sphericalangle \mathrm{.}}\hfill \end{array}}$

Tegyük fel indirekt módon, hogy ${\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}{\alpha }_3\in \left[2\pi /\mathrm{3,}\pi \right]$. Fölhasználva, hogy a koszinuszfüggvény a $\left[2\pi /\mathrm{3,}\pi \right]$ intervallumon monoton csökkenő, az alábbiakat kapjuk:

${\displaystyle \begin{array}{cc}\hfill {\displaystyle {\Vert {\text{a}}_1+{\text{a}}_2+{\text{a}}_3\Vert }^2}& {\displaystyle ={\Vert {\text{a}}_1\Vert }^2+{\Vert {\text{a}}_2\Vert }^2+{\Vert {\text{a}}_3\Vert }^2+2\langle {\text{a}}_1\mathrm{,}{\text{a}}_2\rangle +2\langle {\text{a}}_2\mathrm{,}{\text{a}}_3\rangle +2\langle {\text{a}}_3\mathrm{,}{\text{a}}_1\rangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle =3+2\left(\text{cos}{\alpha }_1+\text{cos}{\alpha }_2+\text{cos}{\alpha }_3\right)\le 3+2\cdot 3\cdot \left(-\frac{1}{2}\right)=0.}\hfill \end{array}}$

Ez csak úgy teljesülhet, ha ${\text{a}}_1+{\text{a}}_2+{\text{a}}_3=\text{0}$. Ám ekkor az ${\text{a}}_1$, ${\text{a}}_2$, ${\text{a}}_3$ vektorok egy síkban vannak, ami ellentmondás.  $\square$

 

Mindezek birtokában már megfogalmazhatjuk és igazolhatjuk fő eredményünket. Ez az eredmény szükséges feltételeket ad arra nézve, hogy egy hálózat adott véges ponthalmaz legrövidebb hálózata legyen.

 

Tétel. Ha $H$ véges síkbeli ponthalmaz, $\text{G}$ ennek legrövidebb hálózata, akkor
$\left(i\right)$ $\text{G}$ olyan fagráf, melynek élei egyenes szakaszok;
$\left(ii\right)$ minden alappontból legfeljebb három él indul és legalább $2\pi /3$ szögben;
$\left(iii\right)$ minden csomópontból pontosan három él indul és pontosan $2\pi /3$ szögben;
$\left(iv\right)$ élek csak alappontban vagy csomópontban találkozhatnak;
$\left(v\right)$ $\text{G}$ teljes egészében H konvex burkán belül halad.
Továbbá, a csomópontok száma legalább kettővel kevesebb az alappontok számánál. Végezetül, ha $H$ térbeli halmaz, akkor az előzőek mellett még az is teljesül, hogy bármelyik csomópontból induló élek közös síkban vannak.

 

Bizonyítás. Világos, hogy ha $\text{G}$ legrövidebb hálózat, akkor összefüggő, körmentes, és élei egyenes szakaszok. Vagyis, $\text{G}$ eleget tesz az $\left(i\right)$ tulajdonságnak.
Tegyük fel indirekt módon, hogy valamely $\text{G}$-beli $A$ csúcs foka legalább négy. Tekintsünk egy olyan $A$ középpontú zárt körlapot, amely nem tartalmaz további csúcsot. Az indirekt feltétel szerint létezik két olyan $A$-ból induló él, melyek a körlap határát a $B$ és $C$ pontokban metszve, egyenlő szárú és hegyesszögű $ABC$ háromszöget alkotnak. A 2. lemma miatt ennek $P$ izogonális pontjára

$\begin{array}{c}{\displaystyle AP+BP+CP<AB+AC}\end{array}$

teljesül. Vagyis, az $A$ csúcsból induló $AC$ és $BC$ szakaszokat törölve, majd $P$ beiktatásával az $AP$, $BP$, $CP$ szakaszokat fölvéve, az eredetinél rövidebb összefüggő hálózat nyerhető. Ez azonban ellentmond $\text{G}$ minimalitásának. Tehát bármely csúcs foka legfeljebb három. Nyilvánvaló továbbá, hogy csomópont foka nem lehet háromnál kevesebb. Mindezekből, szem előtt tartva a 2. lemma és a 3. lemma szögekre vonatkozó feltételeit, a $\left(ii\right)$ és $\left(iii\right)$ tulajdonságokat kapjuk.
A $\left(iv\right)$ feltétel azt mondja ki, hogy $\text{G}$ nem lehet önmetsző. Valóban, ha két él keresztezné egymást, akkor a metszéspontra megismételve az imént látott gondolatmenet fokszámokra vonatkozó részét, rövidíthetnénk a hálózatot.
Jelölje most a $\text{G}$ alappontjainak számát $n$, a beiktatott csomópontokét pedig $m$. Mivel fagráfban az élek száma eggyel kevesebb a csúcsok számánál, ezért $n+m-1=e$, ahol $e$ az élek száma. Másrészt, minden gráfban a fokszámok összege kétszerese az élek számának. Ám a fokszámok összege most $\left(ii\right)$ és $\left(iii\right)$ miatt legalább $n+3m$. Az eddigieket összevetve tehát

$\begin{array}{c}{\displaystyle 2\left(n+m-1\right)\ge n+3m\mathrm{.}}\end{array}$

Ebből rendezéssel kapjuk, hogy $m\le n-2$. Vagyis, a csomópontok száma legalább kettővel kevesebb az alappontok számánál.
Az $\left(v\right)$ tulajdonság bizonyítása ismét indirekt módon történik. Tegyük fel, hogy létezik csomópont a konvex burkon kívül. Mivel a konvex burok előáll a halmazt tartalmazó félsíkok metszeteként, ezért van olyan nyílt félsík, amely tartalmaz csomópontot, de nem tartalmaz alappontot. Válasszunk most egy olyan $P$ csomópontot, amely benne van e félsíkban és távolsága a félsík határegyenesétől maximális. A $P$ ilyen választása lehetséges, hiszen már láttuk, hogy a csomópontok halmaza is véges. Húzzunk párhuzamost a félsík határával $P$-n keresztül. Mivel $P$-ből három él indul páronként $2\pi /3$ szög alatt, ezért lesz olyan $Q$ csomópont, amelyet az imént fölvett párhuzamos elválaszt a $H$ konvex burkától. Ám ekkor az eredeti határegyenestől $Q$ nagyobb távolságra van, mint $P$, ami ellentmondás.
A térbeli esetben csupán a $\left(ii\right)$ és $\left(iii\right)$ állítások megfelelőire térünk ki. Tegyük fel, hogy a $\text{G}$ hálózat $A$ csúcsának foka legalább négy. Tekintsünk egy olyan gömböt, melynek $A$ a középpontja és nem tartalmaz további csúcsot. Válasszunk ki tetszőlegesen három $A$-ból induló élt, s jelölje ezeknek a gömbbel való metszéspontját $B$, $C$, $D$. A 4. lemma miatt az $ABC$, $ACD$, $ADB$ háromszögek egyikében az $A$ csúcsnál lévő szög $2\pi /3$-nál kisebb. Föltehető, hogy ez éppen az $ABC$ háromszög. Ekkor ennek $P$ izogonális pontját véve,

$\begin{array}{c}{\displaystyle AP+BP+CP+AD<AB+AC+AD\mathrm{.}}\end{array}$

Ez azonban nem lehetséges, hiszen $\text{G}$ minimális hálózat. Tehát, $A$, $B$, $C$, $D$ szükségképpen közös síkban vannak. Ugyanezt az érvelést megismételve kapjuk, hogy valamennyi $A$-ból induló él egy síkban van. Azonban ekkor a már igazolt $\left(ii\right)$ és $\left(iii\right)$ tulajdonságok miatt $A$ foka legfeljebb három; sőt, ha csomópontról van szó, pontosan három.  $\square$

 

Az a tény, hogy az alaphalmaz elemszáma segítségével korlátozható a csomópontok (s ezáltal a szóba jövő gráfstruktúrák) száma, kiemelt jelentőséggel bír. Ennek köszönhető ugyanis, hogy bármely véges ponthalmaznak létezik legrövidebb összekötő hálózata. A bizonyítás a megfelelő elméleti háttér birtokában nem nehéz. A gráfelmélet és geometria módszerei mellé segítségül kell hívni az analízist: a hálózat létezése a kompaktság és folytonosság kapcsolatán múlik. E kapcsolat tisztázása azonban már messze túlmutat cikkünk keretein, sőt a középiskola szabta határokon is.
Érdemes hangsúlyoznunk, hogy a konvex burokkal kapcsolatos $\left(v\right)$ tulajdonság bizonyításához rengeteg munka árán, az előző, sőt az utána megfogalmazott tulajdonságok fölhasználásával juthattunk el. Ezzel szemben, a Fermat-feladat megoldásához éppen a konvex burokra vonatkozó 1. lemma jelentette a kiinduló lépést.

 

4. Alkalmazások

Lássuk ezek után, mit ad a főtétel a Gy. 1591. nehezített változatára. Vagyis: hogyan nyerjük az egységnégyzet legrövidebb hálózatát? Mint említettük, a problémának bizonyíthatóan létezik minimumot szolgáltató megoldása. Azt fogjuk megmutatni, hogy ez nem más, mint a korábban már bemutatott fagráf. Ennek topológiai struktúrája egyértelműen, a geometriai pedig szimmetriáktól eltekintve egyértelműen adott.
Az érvelésben szükségünk lesz a következő elemi észrevételre. Ismeretes, hogy bármely háromszög adott csúcsának szögfelezője és a csúccsal szemközti oldal felezőmerőlegese a körülírt körön metszi egymást. Így az $ABC$ háromszög $C$ csúcsa és $P$ izogonális pontja által adott egyenes szögfelező az $ABP$ háromszögben, s ezért az $AB$ oldal felezőmerőlegesét az $ABP$ körülírt körének $D$ pontjában metszi. E pontból az $AB$ oldal $\pi /3$ szög alatt látszik, vagyis $ABD$ szabályos háromszög. Ez az észrevétel egyébként igen jól alkalmazható egyéb pontrendszerek esetére is.
Tekintsük ezek után az egységnégyzet csúcsait, mint az alappontok halmazát. A főtétel $\left(v\right)$ pontja miatt ezek foka nem lehet egytől különböző. Ellenkező esetben ugyanis az ott találkozó élek szöge legfeljebb $\pi /2$, ami ellentmond a $\left(ii\right)$ tulajdonságnak. A keresett hálózatban tehát négy elsőfokú csúcs szerepel, valamint néhány további, három fokú csomópont. Könnyen adódik, hogy a csomópontok száma kettő. Ilyen típusú fagráfból pontosan egy létezik, mégpedig az, amelyet korábban már megadtunk. Vagyis, a topológiai struktúra egyértelmű.
A geometriai struktúra lényegi egyértelműségének igazolásához vegyük figyelembe, hogy átlós alappontok nem csatlakozhatnak közös csomóponthoz. Valóban, két átlós alappont közti út két részre bontja a négyzetlapot, s mivel a főtétel $\left(v\right)$ pontja szerint a hálózat a négyzetlapon belül marad, a másik átlós pár közötti út metszené az előbbit. Ez azonban $\left(iv\right)$ miatt nem lehetséges.
Tekintsük tehát azt a lehetőséget, amikor két szomszédos alappont csatlakozik közös csomóponthoz. A két csomópont által meghatározott egyenes e háromszögnek szögfelezője, így van közös pontja a két alappont felezőmerőlegesével (mégpedig a körülírt körön). Ugyanez teljesül a másik két alappont és a hozzájuk csatlakozó csomópont által meghatározott háromszögre. Tehát a csomópontok által meghatározott egyenes mindkét szemközti oldal felezőmerőlegeséről tartalmaz egy-egy pontot; ámde a két felezőmerőleges azonos, így egybeesik a csomópontok által meghatározott egyenessel. Nyilván párhuzamos oldalpárok bármelyikének alappontjaiból kiindulva ugyanazt a hálózatot kapjuk. Minthogy két párhuzamos oldalpár van, ezért két (forgatással fedésbe hozható) hálózat keletkezik.
A főtétel egyébként más ponthalmazok esetében is igen hatékonyan használható. A teljesség igénye nélkül néhány ilyen esetet feladat formájában fogalmazunk meg. Külön figyelmet érdemel a szabályos hatszög csúcsait összekötő legrövidebb hálózat kérdése. A főtételnek eleget tevő gráfsturktúra ugyanis ekkor már nem egyértelmű. S a burjánzásnak indult szerkezeti gazdagság dacára, a legjobb megoldás egyben a legegyszerűbb $\text{...}$

 

Feladat. Határozzuk meg a szabályos ötszög csúcshalmazához tartozó legrövidebb hálózatot. Igazoljuk, hogy e hálózat szimmetriáktól eltekintve egyértelmű, és adjuk meg teljes hosszát.

 

Feladat. Igazoljuk, hogy a szabályos hatszög csúcshalmazához tartozó, a főtétel kívánalmainak eleget tevő fagráfból három típus lehetséges. Bizonyítsuk be, hogy ezek geometriai helyzete szimmetriáktól eletekintve egyértelmű. Mennyi a legrövidebb hálózat hossza?

 

Feladat. Határozzuk meg a szabályos tetraéder csúcshalmazához tartozó legrövidebb hálózatot. Igazoljuk, hogy e hálózat szimmetriáktól eltekintve egyértelmű, és adjuk meg a teljes hosszát.

 

5. Megjegyzések

Végezetül, érdemes még néhány sort áldoznunk a bemutatott témakör fordulatokban gazdag, izgalmas történeti hátterének vázlatos ismertetésére.
Az $n=3$ speciális eset, vagyis az (F) minimum feladat, vélhetően René Descartes (1596‐1650) problémafölvetésétől ihletve [6], Pierre de Fermat (1607‐1665) révén jutott el a kor matematikusaihoz [7]. A jelenlegi adatok birtokában, a kötött eset első megoldója Evangelista Torricelli (1608‐1647), míg a lebegő eseté Bonaventura Francesco Cavalieri (1598‐1647) volt (lásd a [21] és [3] összegyűjtött műveket). A kötött esetnek, vagyis a 2. lemma állításának elegáns bizonyítása Hofmantól származik [12], és ugyancsak ez található Reiman István könyvében [17]. Harold Scott MacDonald Coxeter (1907‐2003) szintén ezt a megközeltést ismerteti [5], sőt kiterjeszti a lebegő esetre. A probléma térbeli kiterjesztését biztosító 4. lemma alapgondolata Gilbert és Pollack [9] dolgozatából származik. További érdekes matematikai és történeti részletek találhatók a Fermat‐Torricelli‐Cavalieri problémakörrel kapcsolatban Szmerka Gergely cikkében [20].
Az $n=4$ eset 1811-ben bukkant föl először. A probléma megfogalmazása és megoldása Joseph Diaz Gergonne (1771‐1859) nevéhez fűződik. Az általános esettel kapcsolatban számos alapvető eredményt, így például a szögfeltételt és a fokszám feltételt sikerült megkapnia. Érvelésében nem az analízis eszköztárát, hanem Torricelli módszerét alkalmazta.
Természetesen nem maradhat ki Carl Friedrich Gauss (1777‐1855) neve sem a kortörténeti háttérből. Az $n=4$ speciális esetet 1836-ban egyik kortársa, Heinrich Christian Schumacher dán-német csillagász (1780‐1850) vetette föl neki levélben. Igen vázlatos megoldást javasolt ugyan Gauss, azonban sem akkor, sem később nem foglakozott behatóan a problémával. Amint válaszleveléből világosan kiderül, mégis látta benne a lehetőséget: ,,Jómagam úgy vélem, hogy e probléma kiválóan alkalmas arra, hogy tanítványaink figyelmébe ajánljuk.''
Gauss ezúttal sem tévedett: Karl Bopp (1856‐1905) doktori értekezése 1879-ben pontosan e témát dolgozta föl [1]. Az $n=4$ eset részletes analitikus tárgyalása mellett Bopp kitért az $n=5$ esetre, sőt elegáns módszerrel képletet adott az úgynevezett teljes topológiák számának meghatározására.
A probléma 1934-ben ismét fölbukkant, ezúttal két cseh matematikus, Vojtěch Jarník (1897‐ 1970) és Milǒs Kössler (1884‐1961) dolgozatában [14]. Fő eredményük lényegében azonos az általunk ismertetett tétellel, bár módszerük különbözik a miénktől. Alkalmazásként kitértek a négyzet és a szabályos ötszög esetére. Szép bizonyítást adtak arra, hogy $n\ge 13$ esetén a szabályos $n$-szög legrövidebb hálózata a kerület mentén halad, egy oldal elhagyásával. Mivel dolgozatuk csehül íródott, ezért eredményeik lényegében rejtve maradtak a tudományos világ előtt. Eredeti dolgozatuk első részének angol változata 2008-ban jelent meg Korte és Nesětřil jóvoltából [15].
Az az elszigeteltség, amely Jarník és Kössler eredményeit övezte, az egész témakör végzetszerű jellemzője. A legrövidebb hálózatok kutatása újra és újra előtérbe került, hogy aztán a feledés homályába süllyedjen. A kutatók lényegében nem értesültek egymás eredményeiről. Nem csoda hát, hogy Courant és Robins népszerű könyve [4] a témakört Jakob Steiner (1796‐1863) nevéhez fűzte, holott Steinernek semmi köze nem volt ahhoz.
Az 1960-as években a problémakör ismételt lendületet kapott és virágzásnak indult. Ennek oka a fontos alkalmazások mellett a számítógépek fejlődése, melyek lehetővé tették a közelítő algoritmusok megvalósítását. A megjelent cikkek sokáig a Steiner-fa probléma elnevezést használták, ami az előzőek miatt nem is meglepő. A prioritás kérdésével a már említett [15] cikk mellett foglakozik Hwang, Richards és Winter tanulmánya [13]. A legteljesebb történeti áttekintést azonban Brazil, Graham, Thomas és Zachariasen átfogó műve jelenti [2].

 

Hivatkozások

[1]	Bopp, K.: Üeber das kürzeste Verbindungssystem zwischen vier Punkten, doktori értekezés, Universität Göttingen (1879).

[2]	Brazil, M., Graham, R. L., Thomas, D. A. and Zachariasen, M.: On the history of the Euclidean Steiner tree problem, Arch. Hist. Exact Sci., DOI 10.1007/s00407-013-0127-z.

[3]	Cavalieri, B.: Exercitationes Geometricae Sex (1647).

[4]	Courant, R. és Robbins, H.: Mi a Matematika?, Gondolat Kiadó (Budapest, 1966).

[5]	Coxeter, H. S. M.: A geometriák alapjai, Műszaki Könyvkiadó (Budapest, 1987).

[6]	Descartes, R.: Oeuvres de Descartes, Vol. II. (ed. J. Vrin) (Paris, 1896).

[7]	de Fermat, P., Oeuvres, Vol. I. (1891).

[8]	Gergonne, J. D.: Solutions purement géométriques des problŠmes de minimis proposés aux pages 196, 232 et 292 de ce volume, et de divers autres problŠmes analogues, Annales Math. Pures Appl., 1 (1810), 375‐384.

[9]	Gilbert, E. N. and Pollak, H. O.: Steiner minimal trees, SIAM J. Appl. Math., 16 (1968), 1‐29.

[10]	Herczeg J. és Reiman I.: Sík mezőben hármas út $\text{...}$, Élet és Tudomány melléklete, diák-IX‐X-oldal, 1998.

[11]	Herczeg J. és Reiman I.: A háromszög izogonális pontja, Élet és Tudomány melléklete, diák-XXV‐XXVI-oldal, 1998.

[12]	Hofman, J. E.: Elementare Lösung einer Minimumsaufgabe, Zeitschr. Math.-Naturwiss Unterr., 60 (1929), 22‐23.

[13]	Hwang, F. K. and Richards, D. S. and Winter, P.: The Steiner tree problem, Ann. Discrete Math., 53 (1992), North-Holland Publishing Co. (Amsterdam).

[14]	Jarník, V. and Kössler, M.: 0 minimálních grafech obsahujících n daných bodu, Čas. Pěstování Mat., 63 (1934), 223‐235.

[15]	Korte, B. and Nešetřil, J.: Vojtěch Jarnik's work in combinatorial optimization, Discrete Math., 235 (2001), 1‐17.

[16]	Pólya Gy.: Indukció és analógia, Gondolat Kiadó (Budapest, 1988).

[17]	Reiman I.: Geometria és határterületei, Gondolat Kiadó (Budapest, 1986).

[18]	Steinhaus, H.: Matematikai kaleidoszkóp, Gondolat Kiadó (Budapest, 1984).

[19]	Szabó G.: Shortest networks of finite sets, M.Sc. Thesis (Supervisor: M. Bessenyei), University of Debrecen (Debrecen, 2017).

[20]	Szmerka G.: Ízelítő a Fermat‐Torricelli problémakörből, KöMaL, 58 (2008), 194‐201.

[21]	Torricelli, E.: De maximis et minimis, in: Opere di Evangelista Torricelli (ed. Loria, G. and Vassura), G. Faenza (Italy, 1919).