Cím:	Megoldásvázlatok a 2017/1. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Vancsó Ödön ,  Varga Péter
Füzet:	2017/február, 78 - 87. oldal	PDF  |  MathML
Hivatkozás(ok):	2017/január: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Adott a valós számok halmazán értelmezett $f$ és $g$ függvény: $\begin{array}{c}{\displaystyle f\left(x\right)=-x^2-3x+4\text{és}g\left(x\right)=x^2+2x-3.}\end{array}$ $a)$ Adjuk meg az $f\circ g$ függvény hozzárendelési szabályát. $($Az összetett függvény definíciója: $f\circ g\left(x\right)=f\left(g\left(x\right)\right)\mathrm{.})$ $b)$ Van-e olyan $x_0$ hely, ahol az $f$ és $g$ függvényekhez húzható érintők párhuzamosak egymással? $c)$ Számítsuk ki az $f$ és $g$ függvények grafikonja által közbezárt korlátos terület nagyságát.  (14 pont)   Megoldás. $a)$ $\begin{array}{c}{\displaystyle \left(f\circ g\right)\left(x\right)=f\left(g\left(x\right)\right)=-{\left(x^2+2x-3\right)}^2-3\left(x^2+2x-3\right)+4=-x^4-4x^3-x^2+6x+4.}\end{array}$ $b)$ Ha valamely $x_0$ helyen a két függvényhez húzható érintők párhuzamosak egymással, akkor $f\text{'}\left(x_0\right)=g\text{'}\left(x_0\right)$, vagyis $-2x_0-3=2x_0+2$, ahonnan $x_0=-\frac{5}{4}$. Tehát van ilyen $x_0$ hely: $x_0=-\frac{5}{4}$. $c)$ Az $f$ és $g$ függvényt derékszögű koordináta-rendszerben ábrázolva az $f$ függvény képe egy lefelé nyíló parabola, melynek két zérushelye $-4$ és 1, a $g$ függvény képe pedig egy felfelé nyíló parabola, melynek zérushelyei $-3$ és 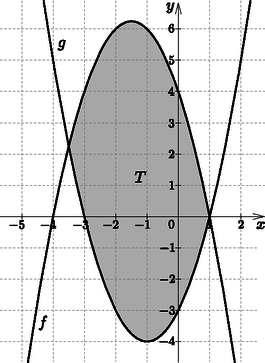1.     A két függvény metszéspontjait (az integrálszámítás határait) az $f\left(x\right)=g\left(x\right)$ egyenlet gyökei adják: $-x^2-3x+4=x^2+2x-3$, ahonnan $x_1=-\frac{7}{2}$ és $x_2=1$. A keresett $T$ területet integrálszámítással határozhatjuk meg: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =\underset{-\frac{7}{2}}{\overset{1}{\int }}\left(-x^2-3x+4-x^2-2x+3\right)\text{d}x=\underset{-\frac{7}{2}}{\overset{1}{\int }}\left(-2x^2-5x+7\right)\text{d}x=}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={\left[-2\cdot \frac{x^3}{3}-5\cdot \frac{x^2}{2}+7x\right]}_{-\mathrm{3,5}}^1=\frac{243}{8}\mathrm{.}}\hfill \end{array}}$   2. A derékszögű koordináta-rendszerben az $ABC$ háromszög csúcsai: $A\left(-4;-3\right)$, $B\left(6;-3\right)$ és $C\left(1;12\right)$. $a)$ Mennyi az $\overrightarrow{AS}$ és a $\overrightarrow{BS}$ vektorok skalárszorzata, ha $S$ az $ABC$ háromszög súlypontja? $b)$ Mekkora és milyen irányú szöggel kell elforgatni az $ABC$ háromszöget a $C$ csúcs körül, hogy az $AC$ oldal párhuzamos legyen az ordinátatengellyel?  (11 pont)   Megoldás. $a)$ Az $ABC$ háromszög $S$ súlypontjának koordinátái a csúcsok megfelelő koordinátáinak számtani közepe: $\begin{array}{c}{\displaystyle S\left(\frac{-4+6+1}{3};\frac{-3-3+12}{3}\right)=\left(1;2\right)\mathrm{,}}\end{array}$ ezért $\overrightarrow{AS}=\left(5;5\right)$, $\overrightarrow{BS}=\left(-5;5\right)$, és így $\overrightarrow{AS}\cdot \overrightarrow{BS}=0$. $b)$ Mivel az $AB$ oldal párhuzamos az $x$ tengellyel, ezért a háromszög $CT$ magassága párhuzamos lesz az $y$ tengellyel. Ha az $ACT$ szöget $\alpha$-val jelöljük, akkor a háromszöget a $C$ csúcs körül éppen $+\alpha$ szöggel kell elforgatni, hogy az $AC$ oldal párhuzamos legyen az $y$ tengellyel.     Az $ACT$ derékszögű háromszögben $\text{tg}\alpha =\frac{5}{15}$, ahonnan $\alpha \approx 18\mathrm{,}{43}^{\circ }$. Tehát az $ABC$ háromszöget kb. $+18\mathrm{,}{43}^{\circ }$-os szöggel kell elforgatni a $C$ csúcs körül.   3. Egy konyhán egy $5$ literes kondérban tésztafőzésre forralnak vizet. A vízbe 50 gramm sót tettek, amit a főszakács sokall, ezért egy nagy fél literes merőkanállal kivesz az oldott sós vízből, és a helyére egy merőkanál tiszta vizet tesz. Alapos keverés után megkóstolja a vizet, de még mindig túl sósnak találja, ezért a sós vízből ismét kivesz fél litert, és a hiányt tiszta vízzel pótolja. A kóstolás után még egyszer utoljára megismétli az előbbi műveletet. Tételezzük fel, hogy minden művelet előtt a só egyenletesen oldódott, és a térfogat-növekedéstől, amit betétele okozott, tekintsünk el. $a)$ Mennyi só maradt a vízben? Az eredményt tizedgrammra kerekítve adjuk meg. $b)$ Hányszor kellene a fenti műveletet megismételni ahhoz, hogy legfeljebb 25 gramm só maradjon a vízben?  (13 pont)   Megoldás. $a)$ Mivel a kanál térfogata tizedrésze a kondér térfogatának, ezért a sótartalomnak is mindig a tizedét vesszük ki. Az első lépésben kivett só mennyisége 5 gramm, hiszen fél liter vízben 5 gramm só van. A második lépésben ismét a még meglevő sómennyiség tizedét vesszük ki, azaz $50-5=45$ grammból 4,5 grammot. A harmadik lépésben már csak $45-4\mathrm{,}5=40\mathrm{,}5$ gramm só maradt a vízben, melynek tizedét kivéve 4,05 grammot veszünk ki. Tehát a megmaradt só mennyisége $40\mathrm{,}5-4\mathrm{,}05=36\mathrm{,}45$ gramm, ami egy tizedesjegyre kerekítve 36,5 gramm. $b)$ Ha a fenti folyamatban $n$ lépést végzünk el, akkor az oldatban maradó só mennyiségét az $50\cdot 0\mathrm{,}{9}^n$ összefüggés adja meg, hiszen minden lépésben a megmaradt só mennyiségének 10%-át vesszük ki. A feladat szövege alapján megoldandó az alábbi egyenlőtlenség: $\begin{array}{c}{\displaystyle 50\cdot 0\mathrm{,}{9}^n\le 25.}\end{array}$ (Az egyenlőtlenséget rendezve, majd mindkét oldal tízes alapú logaritmusát véve:) $\begin{array}{c}{\displaystyle \text{lg}0\mathrm{,}{9}^n\le \text{lg}0\mathrm{,}5.}\end{array}$ (A logaritmus azonosságát felhasználva, majd rendezve:) $\begin{array}{c}{\displaystyle n\ge \frac{\text{lg}0\mathrm{,}5}{\text{lg}0\mathrm{,}9}\approx 6\mathrm{,}58.}\end{array}$ Mivel $n$ csak egész szám lehet, ezért a folyamatot legalább 7-szer kell megismételni.   4. Egy gimnázium $9.$ osztályos tanulói év végén rendelték meg iskolájukban a következő tanévhez szükséges tankönyveket. Összesen $7$ fajta könyvet rendelhettek, minden tantárgyból egyet-egyet. Minden gyerek kapott egy megrendelőlapot, ahol a megfelelő mezőbe tett X jellel jelezhette rendelési szándékát. (Az alábbi táblázatnak megfelelő diák a magyar, történelem és kémia könyveket rendelte meg.)   ${\displaystyle \begin{array}{|ccccccc|}\hline \hfill {\displaystyle \text{magyar}}\hfill & \hfill {\displaystyle \text{ matematika}}\hfill & \hfill {\displaystyle \text{ történelem}}\hfill & \hfill {\displaystyle \text{ angol}}\hfill & \hfill {\displaystyle \text{ földrajz}}\hfill & \hfill {\displaystyle \text{ fizika}}\hfill & \hfill {\displaystyle \text{ kémia }}\hfill \\ \hfill {\displaystyle \text{<span style="font-weight: bold;">X</span>}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">X</span>}}\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle }\hfill & \hfill {\displaystyle \text{<span style="font-weight: bold;">X</span> }}\hfill \\ \hline\end{array}}$   A tankönyvrendelések összesítésekor a tankönyvfelelős megállapította, hogy nem volt olyan tanuló, aki egyetlen könyvet sem rendelt és nem volt két olyan diák, akik pontosan ugyanazokat a könyveket rendelték volna meg. $a)$ Legfeljebb hány diák jár ennek az iskolának a $9.$ évfolyamára? A 9.B. osztálynak $24$ tanulója van, fiúk és lányok vegyesen. Az osztályból két tanulót véletlenszerűen kiválasztunk. $b)$ Hány fiú és hány lány jár az osztályba, ha annak a valószínűsége, hogy a kiválasztott diákok különböző neműek, a lehető legnagyobb?  (13 pont)   Megoldás. $a)$ I. megoldás. Mivel nem volt két olyan diák, akik pontosan ugyanazokat a könyveket rendelték meg, ezért azoknak a diákoknak a száma, akik pontosan egy darab könyvet rendeltek legfeljebb 7. Azoknak a diákoknak a száma, akik pontosan két darab könyvet rendeltek legfeljebb $\left(\genfrac{}{}{0ex}{}{7}{2}\right)$, hiszen 7 darab könyvből ennyiféleképpen lehet kettőt kiválasztani. Hasonló meggondolással számítható ki a három, négy, $\text{...}$, hét darab könyvet rendelők maximális száma, ezért a 9. évfolyamra járó diákok száma legfeljebb $\begin{array}{c}{\displaystyle \left(\genfrac{}{}{0ex}{}{7}{1}\right)+\left(\genfrac{}{}{0ex}{}{7}{2}\right)+\left(\genfrac{}{}{0ex}{}{7}{3}\right)+\left(\genfrac{}{}{0ex}{}{7}{4}\right)+\left(\genfrac{}{}{0ex}{}{7}{5}\right)+\left(\genfrac{}{}{0ex}{}{7}{6}\right)+\left(\genfrac{}{}{0ex}{}{7}{7}\right)=127.}\end{array}$ II. megoldás. A tanulók minden könyvről egyértelműen eldönthetik, hogy megrendelik-e vagy sem, ezért a lehetséges megrendelések (és egyben tanulók) száma legfeljebb $2^7=128$. Mivel olyan diák nem volt, aki egyetlen könyvet sem rendelt meg, ezért az évfolyamra legfeljebb $128-1=127$ tanuló járhat. $b)$ Jelölje a lányok számát $l$, a fiúkét $f$. A feladat szövege alapján $l+f=24$. 24 tanulóból 2-t $\left(\genfrac{}{}{0ex}{}{24}{2}\right)$-féleképpen választhatunk ki, ezért az összes eset száma $\left(\genfrac{}{}{0ex}{}{24}{2}\right)$. 1 lányt és 1 fiút $\left(\genfrac{}{}{0ex}{}{l}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{f}{1}\right)$-féleképpen választhatunk ki, ezért a kedvező esetek száma $\left(\genfrac{}{}{0ex}{}{l}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{f}{1}\right)$. Az $l+f=24$ összefüggést felhasználva a keresett valószínűség: $\begin{array}{c}{\displaystyle P=\frac{\left(\genfrac{}{}{0ex}{}{l}{1}\right)\cdot \left(\genfrac{}{}{0ex}{}{f}{1}\right)}{\left(\genfrac{}{}{0ex}{}{24}{2}\right)}=\frac{l\cdot f}{276}=\frac{l\cdot \left(24-l\right)}{276}=\frac{24l-l^2}{276}=\frac{144-{\left(l-12\right)}^2}{276}\mathrm{.}}\end{array}$ A tört értéke akkor maximális, ha a számlálója maximális. A számlálóban lévő különbség akkor lesz a lehető legnagyobb, ha a négyzetes tag a legkisebb, azaz 0. Ebből következik, hogy $l=12$ és $f=12$. Tehát 12 lány és 12 fiú jár az osztályba.   II. rész     5. Egy trapézban húzzuk be a középvonalat, majd az alapokkal párhuzamosan két szakaszt: az átlók metszéspontján áthaladó, illetve a trapéz területét felező szakaszt. $a)$ Igazoljuk, hogy a behúzott három szakasz hossza rendre az alapok számtani, harmonikus és négyzetes közepe. $b)$ Indokoljuk meg megfelelő ábra alapján az $a)$ feladatban megadott három közép nagyságának sorrendjét.  (16 pont)   Megoldás. $a)$ Tükrözzük az $ABCD$ trapézt a $BC$ szár $F$ felezőpontjára. A tükrözés után kapott $AD\text{'}A\text{'}D$ négyszög paralelogramma, melyben $EE\text{'}=AD\text{'}=A\text{'}D=AB+CD$, illetve $EE\text{'}=2EF$. Az előbbi két egyenlőségből $EF=\frac{AB+CD}{2}$, tehát a trapéz középvonalának hossza valóban az alapok hosszának számtani közepe.     Az $ABD$ háromszög hasonló a $PMD$ háromszöghöz, mert megfelelő szögeik egyenlők, ezért $\frac{x}{a}=\frac{v}{u+v}$. Az $ADC$ háromszög hasonló az $APM$ háromszöghöz, mert megfelelő szögeik egyenlők, ezért $\frac{x}{c}=\frac{u}{u+v}$. Az előbbi két egyenlet megfelelő oldalait összeadva $\frac{x}{a}+\frac{x}{c}=\frac{v}{u+v}+\frac{u}{u+v}=1$, melyből rendezéssel $x=\frac{ac}{a+c}$. Hasonló meggondolással belátható, hogy $y=\frac{ac}{a+c}$, így $\begin{array}{c}{\displaystyle PQ=x+y=\frac{2ac}{a+c}\mathrm{,}}\end{array}$ tehát a trapéz átlóinak metszéspontján át húzott szakasz hossza az alapok harmonikus közepe. Jelölje $RS$ a trapéz alapjaival párhuzamos, annak területét felező szakaszt, melynek hossza $z$. Legyen az $RSCD$ trapéz magassága $m$, az $ABSR$ trapézé pedig $m\text{'}$. Húzzunk párhuzamost az $AD$ szárral a $C$ és az $S$ pontokon keresztül, melyek az $RS$, illetve az $AB$ szakaszt rendre az $N$, illetve a $V$ pontban metszik. 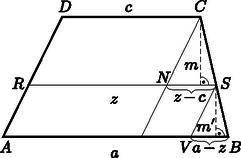    A $VBS$ háromszög hasonló az $NSC$ háromszöghöz, mert megfelelő szögeik egyenlők, ezért $\begin{array}{c}{\displaystyle \frac{a-z}{z-c}=\frac{m\text{'}}{m}\mathrm{.}}\end{array}$ Mivel az $ABSR$ és $RSCD$ trapézok területe egyenlő, ezért $\frac{a+z}{2}\cdot m\text{'}=\frac{z+c}{2}\cdot m$. Az előbbi két egyenletből $\frac{a-z}{z-c}=\frac{z+c}{a+z}$, melyet átrendezve $z^2=\frac{a^2+c^2}{2}$, ahonnan $\begin{array}{c}{\displaystyle z=\sqrt[]{\frac{a^2+c^2}{2}}\mathrm{.}}\end{array}$ Tehát a trapéz területét felező, alapokkal párhuzamos szakasz hossza az alapok hosszának négyzetes közepe. $b)$ Mivel az ábrán $c<a$, ezért a trapéz területét felező szakasz a középvonal alatt, míg az átlók metszéspontján áthaladó szakasz a középvonal felett helyezkedik el. Ebből következik, hogy a három közép nagysága növekvő sorrendben: harmonikus, számtani, négyzetes.   6. Egy mobiltelefonokat gyártó cég minden évben ősszel jelenteti meg legújabb csúcskészülékét. Az újonnan kapható okostelefon kijelzőjén összesen $273460$ pixellel több képpont található, mint az egy évvel korábban megjelent azonos típusú régebbi telefonén. Ez azért van, mert az új telefon széltében $\mathrm{198,}$ hosszában pedig $110$ pixellel több képpontot tud kijelezni. $a)$ Mekkora (hányszor hány pixel) az új telefon képernyőfelbontása, ha a régebbi készülék kijelzőjén összesen $727040$ képpont található? A gyártó cég szeretné a készülékeladásból származó bevételét maximalizálni, melyet az eladási ár megfelelő meghatározásával szeretne elérni. A cég vezetői az eddigi tapasztalatok alapján azt feltételezik, hogy ha a készüléket 120 000 Ft-ért árusítják, akkor mind az $1000$ telefonra érkezik megrendelés, ha pedig az eladási árat 3 000 Ft-tal megemelik, akkor a rendelések száma $20$ darabbal csökken, és minden további 3000 Ft-nyi emelés újabb $20$ darabbal csökkenti a megrendelések számát. $b)$ Mennyi legyen a készülék eladási ára, hogy a cég bevétele maximális legyen ezen az eladáson?  (16 pont)   Megoldás. $a)$ Jelölje $x$ és $y$ a régebbi telefon kijelzőjén lévő vízszintes és függőleges képpontok számát. A feladat szövege alapján az alábbi egyenletrendszer írható fel: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x\cdot y}& {\displaystyle =727\mathrm{040,}}\hfill \\ \hfill {\displaystyle \left(x+198\right)\cdot \left(y+110\right)}& {\displaystyle =1000500.}\hfill \end{array}}$ A második egyenlet bal oldalán a kijelölt szorzást elvégezve, majd az egyenletet rendezve a következő (egyszerűbb) egyenletrendszerhez jutunk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle x\cdot y}& {\displaystyle =727\mathrm{040,}}\hfill \\ \hfill {\displaystyle 110x+198y}& {\displaystyle =251680.}\hfill \end{array}}$ Az első egyenletből az egyik ismeretlent kifejezve, majd azt a második egyenletbe behelyettesítve rendezés és összevonás után a $99y^2-125840y+39987200=0$ másodfokú egyenletet kapjuk, melynek gyökei $y_1=640$ és $y_2=631\mathrm{,}\dot{1}$. Utóbbi a törtarány miatt nyilván nem megoldása a feladatnak, ezért $x_1=1136$. Ellenőrzés: A régebbi telefon kijelzőjén $1136\cdot 640=727040$, míg az új telefon kijelzőjén $\left(1136+198\right)\cdot \left(640+110\right)=1000500$ képpont található, ami valóban 273 460 pixellel több. Tehát az új telefon képernyőfelbontása $1334\times 750$ pixel. $b)$ Jelölje $x$ a 3000 Ft-tal történő emelések számát. Ekkor a telefon ára $\begin{array}{c}{\displaystyle \left(120000+3000x\right)\text{Ft, }}\end{array}$ az eladott darabszám pedig $\left(1000-20x\right)$. A $\left(B\right)$ bevétel ezer Ft-ban számolva: $\begin{array}{c}{\displaystyle B\left(x\right)=\left(120+3x\right)\cdot \left(1000-20x\right)=60\cdot \left(-x^2+10x+2000\right)\mathrm{.}}\end{array}$ Szélsőérték ott lehet, ahol $B\text{'}\left(x\right)=0$, ezért $-2x+10=0$, amiből $x=5$. $x=5$ esetén $B\text{'}$ előjelet vált, tehát $B$-nek valóban maximuma van. Tehát a bevétel akkor lesz maximális, ha a telefon árát $120000+5\cdot 3000=135000$ Ft-ban határozzák meg.   7. $a)$ Bizonyítsuk be, hogy nincs olyan hétpontú egyszerű gráf, amelyben minden pont fokszáma különböző. $b)$ Egy hétpontú egyszerű gráf csúcsai között egyetlen olyan van, melynek fokszáma még egyszer előfordul. Melyik lehet ez a fokszám? Adjunk meg egy, a feladat feltételeinek megfelelő gráfot.  (16 pont)   Megoldás. $a)$ I. megoldás. Egy hétpontú egyszerű gráfban egy pont fokszáma maximum 6 lehet (nincsenek hurok- és többszörös élek), ezért a hét pontra hét lehetőség jut: 0; 1; 2; 3; 4; 5; 6. Ha van 6 fokszámú pont, akkor nem lehet 0 fokszámú, így csak két lehetőség marad: 0; 1; 2; 3; 4; 5 vagy 1; 2; 3; 4; 5; 6. Mivel 7 pontunk van, a skatulyaelv szerint az egyik fokszámnak legalább kétszer kell előfordulnia, így biztosan nincs a feladat feltételeinek megfelelő gráf. II. megoldás. Egy hétpontú egyszerű gráfban, ha minden pont fokszáma különböző, akkor a csúcsok fokszámainak lehetséges értékei 0; 1; 2; 3; 4; 5; 6 (nincsenek hurok- és többszörös élek). Mivel bármely egyszerű gráfban a fokszámok összege az élek számának kétszerese, ezért gráfunknak $\frac{21}{2}=10\mathrm{,}5$ éle lenne, ami nem lehetséges. Tehát valóban nincs a feladat feltételeinek megfelelő gráf. $b)$ Két eset lehetséges: 0; 1; 2; 3; 4; 5; $x$ vagy 1; 2; 3; 4; 5; 6, $x$. Nézzük először a 0; 1; 2; 3; 4; 5; $x$ esetet. $x$ értéke nem lehet 0; 2; 4, hiszen ekkor a kapott gráfban a fokszámok összege páratlan lenne, ami a fokszámtétel miatt nem lehetséges. $x$ értéke nem lehet 5 sem, ugyanis ekkor mindkét 5 fokszámú csúcs az izolált pont kivételével mindegyik másikkal össze lenne kötve, így nem lenne 1 fokszámú csúcs. $x$ továbbá 1 sem lehet, mert ebben az esetben az 5 fokszámú csúcs hasonlóan össze van kötve az izolált pont kivételével mindegyik másikkal, az 1 fokszámú csúcsok pedig csak az 5 fokszámúval. Ebből következik, hogy már csak az a kérdés, hogy a 2, 3 és 4 fokszámú csúcsok melyik másik csúcsokkal lehetnek összekötve. Mivel az 5 fokszámú csúccsal az előbbi csúcsok mindegyike össze van kötve, ezért a 0, az 1 és az 5 fokszámú négy csúcsot elhagyva egy önálló, 1, 2, 3, fokszámú hárompontú egyszerű gráfot kapnánk, mely nyilván nem lehetséges, hiszen a gráf egyszerű. Tehát csak a 3-as fokszám ismétlődhet, így a feladat feltételeinek megfelelő gráf:     Nézzük a második esetet: 1; 2; 3; 4; 5; 6; $x$. $x$ értéke hasonlóan nem lehet 2; 4; 6, hiszen ekkor a kapott gráfban a fokszámok összege ismét páratlan lenne, ami a fokszámtétel miatt szintén nem lehetséges. $x$ értéke ugyancsak nem lehet 5, ugyanis ekkor mindkét 5 fokszámú csúcsot össze kellene kötni a 2 fokszámú csúccsal, ami nem lehetséges, hiszen a 6 fokszámú csúcs biztosan össze van kötve vele, és így a fokszáma 3 lenne. $x$ továbbá 1 sem lehet, hiszen ha az előbbi eset meggondolásához hasonlóan a gráfból elhagyjuk a 6 és a két 1 fokszámú csúcsokat, akkor egy négypontú, önálló egyszerű gráfot kapunk, melynek fokszámai 1-gyel csökkenek, azaz 1, 2, 3, 4, lesznek, ami ismét nem lehetséges, hiszen egy négypontú egyszerű gráfban nem lehet 4 fokszámú csúcs. Tehát ebben az esetben is csak a 3-as fokszám ismétlődhet, így a feladat feltételeinek megfelelő gráf: 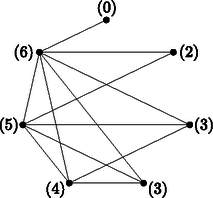  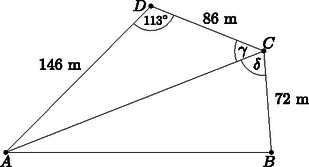    8. A mellékelt ábrán látható négyszög két szögét $(113$ és $116$ fok$)$ és három oldalát (146, 86 és 72 m) ismerjük. Mekkora a négyszög területe?  (16 pont)       I. megoldás. Bontsuk fel az $ABCD$ négyszöget két háromszögre!     Az $ACD$ háromszögből koszinusztétellel $AC=\sqrt[]{{146}^2+{86}^2-2\cdot 146\cdot 86\cdot \text{cos}{113}^{\circ }}\approx 196\mathrm{,}28$ (m). Az $ACD$ háromszögben alkalmazva a szinusztételt $\frac{\text{sin}\gamma }{\text{sin}{113}^{\circ }}=\frac{146}{\mathrm{196,28}}$, ahonnan ($\gamma <{90}^{\circ }$ miatt) $\gamma \approx 43\mathrm{,}{21}^{\circ }$. Ekkor az $ABC$ háromszögben $\delta ={116}^{\circ }-\gamma \approx 72\mathrm{,}{79}^{\circ }$. Az $ABCD$ négyszög területe az $ABC$ és $CDA$ háromszögek területének összege: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =T_{ABC}+T_{CDA}=\frac{72\cdot 196\mathrm{,}28\cdot \text{sin}72\mathrm{,}{79}^{\circ }}{2}+\frac{146\cdot 86\cdot \text{sin}{113}^{\circ }}{2}\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx 6749\mathrm{,}42+5778\mathrm{,}93\approx 12528{\text{m}}^2\mathrm{.}}\hfill \end{array}}$ II. megoldás. Egészítsük ki az $ABCD$ négyszöget háromszöggé. 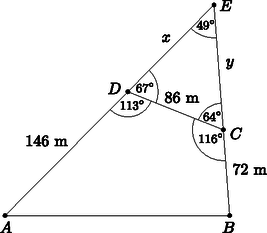    Az $EDC$ háromszög ismeretlen szögei: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle EDC\sphericalangle }& {\displaystyle ={180}^{\circ }-{113}^{\circ }={67}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle ECD\sphericalangle }& {\displaystyle ={180}^{\circ }-{116}^{\circ }={64}^{\circ }\mathrm{,}}\hfill \\ \hfill {\displaystyle DEC\sphericalangle }& {\displaystyle ={180}^{\circ }-\left({64}^{\circ }+{67}^{\circ }\right)={49}^{\circ }\mathrm{.}}\hfill \end{array}}$ Alkalmazzuk az $EDC$ háromszögben a szinusztételt: $\begin{array}{c}{\displaystyle \frac{x}{86}=\frac{\text{sin}{64}^{\circ }}{\text{sin}{49}^{\circ }}\mathrm{,}}\end{array}$ amiből $x\approx 102\mathrm{,}42$ (m), és $\begin{array}{c}{\displaystyle \frac{y}{86}=\frac{\text{sin}{67}^{\circ }}{\text{sin}{49}^{\circ }}\mathrm{,}}\end{array}$ ahonnan $y\approx 104\mathrm{,}89$ (m), így $AE=146+x\approx 248\mathrm{,}42$ (m) és $BE=72+y\approx 176\mathrm{,}89$ (m). Az $ABCD$ négyszög területe az $ABE$ és $CDE$ háromszögek területének különbsége: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T}& {\displaystyle =T_{ABE}-T_{CDE}=\frac{248\mathrm{,}42\cdot 176\mathrm{,}89\cdot \text{sin}{49}^{\circ }}{2}-\frac{102\mathrm{,}42\cdot 104\mathrm{,}89\cdot \text{sin}{49}^{\circ }}{2}\approx }\hfill \\ \hfill {\displaystyle }& {\displaystyle \approx 16582\mathrm{,}25-4053\mathrm{,}9\approx 12528{\text{m}}^2\mathrm{.}}\hfill \end{array}}$   9. Egy városban a fiatalok körében vizsgálódtak a futballrajongók és az agresszív viselkedésre hajlamos személyek között. A következőket állapították meg: $•$ Az agresszivitást mutató fiatalok $70\%$-a futballrajongó. $•$ Az agresszívnek nem mondhatók között csupán $30\%$ futballrajongó van. $•$ A futballrajongók $60\%$-a mutat agresszivitást. $a)$ A város fiataljainak hány százaléka futballrajongó? $b)$ Mennyire jellemzi a várost a fiatalok agresszivitása? $c)$ A futballrajongó agresszív fiatalok a mérkőzések kb. $15\%$-ában okoznak nagyobb rendőrségi problémát. Mekkora annak a valószínűsége, hogy három mérkőzésen is megússza a helyi rendőrség a beavatkozást, ha feltehetjük, hogy az egyes mérkőzéseken kitört botrányok egymástól függetlenek?  (16 pont)   Megoldás. $a)$ I. megoldás. Jelölje $A$ az agresszívek, $F$ pedig a futballrajongók csoportját. Ekkor a feladat szövege alapján: $P\left(F\mid A\right)=0\mathrm{,}7$, $P\left(F\mid \overline{A}\right)=0\mathrm{,}3$ és $P\left(A\mid F\right)=0\mathrm{,}6$, ahol $P\left(F\right)$ értékét keressük. A feltételes valószínűség definíciója alapján ${\displaystyle \begin{array}{cc}\hfill {\displaystyle P\left(F\mid A\right)}& {\displaystyle ={\displaystyle \frac{P\left(FA\right)}{P\left(A\right)}}=0\mathrm{,}\mathrm{7,}}\hfill \\ \hfill {\displaystyle P\left(F\mid \overline{A}\right)}& {\displaystyle ={\displaystyle \frac{P\left(F\overline{A}\right)}{1-P\left(A\right)}}={\displaystyle \frac{P\left(F\right)-P\left(FA\right)}{1-P\left(A\right)}}=0\mathrm{,}3\text{és}}\hfill \\ \hfill {\displaystyle P\left(A\mid F\right)}& {\displaystyle ={\displaystyle \frac{P\left(FA\right)}{P\left(F\right)}}=0\mathrm{,}6.}\hfill \end{array}}$ A harmadik egyenletből $P\left(FA\right)$ valószínűségét beírva a második egyenletbe $\begin{array}{c}{\displaystyle \frac{0\mathrm{,}4P\left(F\right)}{1-P\left(A\right)}=0\mathrm{,}3.}\end{array}$ Az első és harmadik egyenletből $0\mathrm{,}6P\left(F\right)=0\mathrm{,}7P\left(A\right)$, vagyis $P\left(A\right)=\frac{6}{7}P\left(F\right)$, így $\begin{array}{c}{\displaystyle \frac{0\mathrm{,}4P\left(F\right)}{1-\frac{6}{7}P\left(F\right)}=0\mathrm{,}\mathrm{3,}\text{azaz}\frac{2}{5}P\left(F\right)=\frac{3}{10}-\frac{9}{35}P\left(F\right)\mathrm{,}}\end{array}$ ahonnan $\frac{23}{35}P\left(F\right)=\frac{3}{10}$, amiből $P\left(F\right)=\frac{21}{46}\approx 0\mathrm{,}46$, tehát a város fiataljainak körülbelül 46%-a futballrajongó. II. megoldás. Vegyünk 10 agresszív fiatalt, akik közül 7 futballrajongó. Ha $n$ nem agresszív fiatal van, akkor ezek között $0\mathrm{,}3n$ fő futballrajongó. Viszont a 7 agresszív futballrajongó 60%-a az összes futballrajongónak, vagyis $7=\left(7+0\mathrm{,}3n\right)\cdot 0\mathrm{,}6=4\mathrm{,}2+0\mathrm{,}18n$, ahonnan $n=\frac{140}{9}$. Ahhoz, hogy $n$ egész szám legyen, mindent 9-cel kell szorozni, tehát 90 agresszív fiatalból 63 fő futballrajongó, és 140 nem agresszívből 42 fő. E szerint a futballrajongók száma 105, ami a 230-nak kb. 46%-a, ami nyilván független a város lakosságától, hiszen az arány nem változik. $b)$ $P\left(A\right)$ valószínűségét keressük: $\begin{array}{c}{\displaystyle P\left(A\right)=\frac{6}{7}\cdot \frac{21}{46}=\frac{9}{23}\approx 0\mathrm{,}\mathrm{39,}}\end{array}$ tehát a város fiataljainak kb. 39%-a agresszív. $c)$ Mivel az egyes mérkőzéseken kitört botrányok egymástól függetlenek, ezért $0\mathrm{,}{85}^3\approx 0\mathrm{,}61$ annak a valószínűsége, hogy a helyi rendőrség megússza a beavatkozást.