|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész
1. Egy dömper az építkezés és a kavicsbánya között szállít kavicsot. A két hely között 18 km a távolság. Az építkezéstől a bányáig és vissza pontosan óra perc a tiszta szállítási idő.
Mekkora a teherautó sebessége terheletlenül, ha azt tudjuk, hogy terhelve (bányából az építkezésre) 6 km/h-val kisebb átlagsebességgel halad?
100 km-re vetítve a kocsi fogyasztása -kal több terhelve, mint terheletlenül. Mennyi a kocsi terheletlen fogyasztása (liter/100 km mértékegységben), ha az oda-vissza út során összesen 10,8 liter benzint fogyasztott? (12 pont)
Megoldás. (Minden távolságot km-ben, minden idő-mennyiséget órában, és minden sebességet km/h-ban fogunk számolni, és csak a megoldás végén írjuk fel a mértékegységeket.) Az odaút sebessége legyen , ekkor a visszaút (ekkor van tele kővel a dömper) sebessége , míg a két rész-út megtételéhez szükséges idő legyen , illetve .
A feladat szövege alapján: Az egyenletet megoldva:
Innen | |
Ezek közül csak (km/h) lehet a megoldás, mert esetén a visszaút sebessége negatív lenne.
Mivel a két út egyforma hosszú, ezért ha az odaúton liter bezin fogyott, akkor a visszaúton , azaz összesen . Innen , azaz .
Mivel ezt a mennyiséget km alatt fogyasztotta a dömper, ezért a 100 km-re vetített terheletlen fogyasztása: | |
2. Tekintsük a következő rekurzívan megadott sorozatokat: , (ha ), illetve , ha .
Hány olyan indexű tagja van az sorozatnak, ami egész értéket vesz fel?
Hány olyan indexű tagja van a sorozatnak, amelyre teljesül a egyenlőtlenség?
Adjuk meg az összeg pontos értékét. (14 pont)
Megoldás. Először megadjuk a sorozatokat nem rekurzív módon. Mindkét helyen teleszkópos összeget, illetve szorzatot használunk.
és mivel , ezért | |
Míg a másik sorozatra:
Mivel , és ez pontosan akkor egész, ha négyzetszám, ezért (hiszen ) pontosan darab egész tag van -ig.
A egyenlőtlenséget kissé átírva:
Innen adódik, vagyis darab megfelelő tagja van a sorozatnak.
| |
Mivel , így az összeg első két tagjára (az ismert összefüggést fogjuk most és később is használni) , az első három tagjára: | |
és így tovább.
Vagyis | |
3. Három testvérnek, András, Béla és Csaba gazdának külön-külön - hektárnyi földje van. A birtokokból külön-külön - hektár telepített szőlő, amin adott, hogy mit termelnek (nem lenne értelme kiszedni a tőkéket), a másik hektáron viszont három egyéb növény termelése közül választhatnak külön-külön a testvérek (krumpli, rizs, homoktövis). Az elmúlt 120 év bergengóciai regionális ‐ az időjárásra vonatkozó ‐ statisztikái alapján a következő táblázat készíthető az egyes növények hektárra vonatkozó hasznáról (az értékek ezer bergengóc euróban adottak).
a) Mit termeljen András gazda, ha azt szeretné, hogy a várható nyeresége a lehető legnagyobb legyen?
b) Mennyi valamely gazda nyereségének (ami az időjárástól, mint véletlen eseménytől függ) szórása, ha a szőlő mellett a másik 10 hektáron rizst, krumplit, illetve homoktövist termel?
Bergengóciában úgy tartják, hogy ‐ azonos várható nyereség esetén ‐ az a kockázatosabb beruházás, ahol nagyobb a szórás.
c) Béla gazda azt szeretné, hogy a lehető legrosszabb időjárás esetén is a lehető legkevesebb legyen a vesztesége. Igaz-e, hogy neki a legkevésbé kockázatos beruházást kell választania?
d) Csaba gazda egy nagy értékű traktort vett hitelre. Ha az év végén (miután már értékesítette az az évi termést) nem tud visszafizetni 15000 bergengóc eurót, akkor csődbe megy.
Igaz-e, hogy ahhoz, hogy ezt a lehető legnagyobb eséllyel elkerülje: neki a legkockázatosabb beruházást érdemes választania? Mekkora eséllyel menekül meg ekkor a csődtől Csaba gazda? (11 pont)
Megoldás. a) A maradék 10 hektáron az egyes növények várható haszna:
E(rizs)=-5+0+4+7+95=3,E(krumpli)=2+10+9+2+(-8)5=3,E(homoktövis)=3+3+3+3+35=3.
Vagyis bármely növény esetén ugyanakkora a várható nyereség, és mivel a 10 hektár szőlő várható nyeresége: E(szőlő)=5+12+10+4+(-6)5=5, így a várható össznyereség éppen 8000 bergengóc euró.
b) Először készítsünk egy szőlővel összevont táblázatot.
Időjárás aszályos száraz normál csapadékos monszun Időjárás esélye 15 15 15 15 15 Növények haszna az egyes időjárás-típusok esetén(1000 bergengóc euró/10 hektárban)szőlő+rizs 0 12 14 11 3 szőlő+krumpli 7 22 19 6 -14 szőlő+homoktövis 8 15 13 7 -3
Mivel a várható érték 8 volt, így a szórásnégyzetek:
D2(sz+r)=(0-8)2+(12-8)2+(14-8)2+(11-8)2+(3-8)25=30,D2(sz+k)=(7-8)2+(22-8)2+(19-8)2+(6-8)2+(-14-8)25=8065=161,2,D2(sz+h)=(8-8)2+(15-8)2+(13-8)2+(7-8)2+(-3-8)25=1965=39,2.
Innen a három szórás: D(sz+r)=30≈5,48, D(sz+k)=161,2≈12,70, D(sz+h)=39,2≈6,26.
c) A lehető legrosszabb időjárás esetén a lehető legkevesebb veszteség úgy érhető el a fenti módosított táblázat alapján, ha a szőlő mellé rizst telepít Béla gazda, és mivel ekkor a legkisebb a szórás, ezért igaz az állítás.
d) Csaba gazda a kívánt 15000 eurót a lehető legnagyobb eséllyel akkor teremti elő, ha a szőlő mellé krumplit vet. Vagyis neki valóban a legkockázatosabb választásra van szüksége. Ekkor a csőd elkerülésének az esélye: 25.
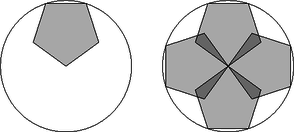
4. Kati néni egy kör alakú asztalra (a bal oldali ábra szerint) feltett egy szabályos ötszög alakú terítőt úgy, hogy a terítő egyik csúcsa egybeesik az asztal középpontjával, míg a terítő két másik csúcsa éppen az asztal kerületére esik.
a) Az asztal hány %-át fedi le Kati néni terítője?
Mari néni egy, az előzővel azonos méretű asztalra négy (az előző terítővel azonos méretű) terítőt tett fel. Az egyik terítőt pontosan úgy, ahogy Kati néni, míg a többi terítőt (a jobb oldali ábra szerint) úgy, mintha az első terítőt rendre elforgatná 90∘, 180∘, 270∘-kal az asztal középpontja körül.
b) Az asztal hány %-át fedi le Mari néni négy terítője együttesen? (14 pont)
Megoldás. a) Mivel hasonlóság erejéig az ábrák mreghatározottak, legyen az asztalok mint körök sugara 1. Nyilván a terítők átlója szintén 1 hosszú. Mivel a szabályos 5-szögek belső szögei 108∘-osak, innen a terítő egy a oldalára (a megfelelő egyenlőszárú háromszögből): sin54∘=12a, azaz a terítő oldalának hossza: Innen a terítőt két, egy csúcsból induló átlójának segítségével három egyenlőszárú háromszögre bontva:
Tterítő=12⋅sin36∘2+2⋅a2⋅sin108∘2=sin36∘2+2⋅sin54∘⋅cos54∘4⋅sin54∘⋅sin54∘==sin36∘+ctg54∘2≈0,6572.
Azaz a terítő az asztalnak sin36∘+ctg54∘2π≈0,2092, vagyis kb. 21%-át fedi le.
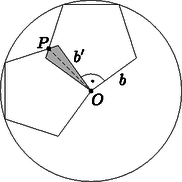
b) Tekintsük az ábrát (melyen két szomszédos terítő látható). A két terítő által közösen lefedett ,,metszet'' (mivel az egész ötszöget 90∘-kal forgattuk el, így a b, b' által bezárt szög is derékszög) egy olyan deltoid, melynek hosszabb oldala azonos a terítő a oldalával, míg szögei rendre 18∘, 108∘, 126∘, 108∘-osak. Először kiszámoljuk a deltoid hosszabb, c átlóját szinusz-tétellel: | asin63∘=csin108∘,amibőlc=sin108∘2sin54∘sin63∘. |
Innen:
tdeltoid=2⋅a⋅csin9∘2=sin108∘⋅sin9∘2⋅sin54∘⋅2sin54∘sin63∘==2sin54∘⋅cos54∘sin9∘2⋅sin54∘⋅2sin54∘sin63∘=cos54∘sin9∘2sin54∘sin63∘.
Mivel a négy terítő összterülete éppen négy ilyen deltoid területével több, mint a lefedett terület:
tlefedett=4⋅sin36∘+ctg54∘2-4⋅cos54∘sin9∘2sin54∘sin63∘==2⋅(sin36∘+ctg54∘-cos54∘sin9∘sin54∘sin63∘)≈2,3735,
ez pedig a teljes asztal tlefedettπ≈0,7555 része. Vagyis a terítők az asztal kb. 76%-át fedik le.
II. rész
5. Véletlenszerűen kiválasztok 0 és 9999 között egy olyan számot, ami tartalmaz 2-es számjegyet. Mekkora az esélye, hogy a kiválasztott számomban több 2-es van a számjegyek között, mint 1-es? (Pl. 2012 ,,kedvező'' tulajdonságú szám, de 2016 nem.) (16 pont)
Megoldás. Először megszámoljuk, hogy összesen hány olyan legfeljebb négyjegyű szám van, ami tartalmaz 2-es számjegyet.
Két apró ötlet: egyszerűbb azokat a számokat megszámolni, melyek nem tartalmaznak 2-es jegyet, illetve minden nem négyjegyű számra olyan négyjegyű számként fogunk tekinteni, melynek első pár jegye 0 (pl. most 17=0017 lesz).
A 2-est nem tartalmazó számok száma: 9⋅9⋅9⋅9=6561, hiszen mind a négy számjegyre 9 lehetőség van, így a 2-est tartalmazó számok száma: n=10000-6561=3439.
Most nézzük meg, hogy közülük hány ,,jó'', azaz hány olyan van, amelyikben kevesebb az 1-es jegy.
‐ Ha mind a négy jegy 2-es, az jó. Ez 1 eset.
‐ Ha három jegy 2-es, az is mind jó. Ez 4⋅9=36 eset. (Hiszen a ,,maradék'' nem 2-es jegy 9-féle lehet és 4 helyre kerülhet.)
‐ Ha két jegy 2-es, akkor minden olyan eset jó, ahol 0, vagy 1 darab 1-es jegy van.
Ha nincs 1-es, akkor a két 2-est (42)=6 helyre tehetjük, a maradék helyekre pedig 8-8-féleképp tehetünk számjegyeket, azaz ekkor 6⋅82=384 jó eset van.
Ha egy darab 1-es van, akkor a két 2-est (42)=6 helyre tehetjük, az 1-est két helyre, a maradék helyre pedig 8-féleképp tehetünk számjegyet, azaz ekkor 6⋅2⋅8=96 jó eset van.
‐ Végül, ha egyetlen jegy 2-es, akkor a számban egyáltalán nem lehet 1-es jegy. Ezt könnyű megszámolni: az egyetlen 2-est 4 helyre helyre tehetem, a maradék helyekre pedig 8-8-8-féleképp tehetek számjegyeket, azaz ekkor 4⋅83=2048 jó eset van.
Vagyis a kedvező esetek száma: k=1+36+(384+96)+2048=2565, és a kérdéses valószínűség: kn=25653439≈0,746.
6. Oldjuk meg az alábbi egyenletrendszert a valós számpárok halmazán:
1=(4x2-8x+74)y2-8y+7,arccosx=arcsiny.
(16 pont)
Megoldás. Az ab=1 egyenlet akkor teljesül, ha az alap a=1, vagy, ha a kitevő b=0, és az a≠0 (bár ez utóbbi megállapodás kérdése), illetve, ha az alap a=-1, és a kitevő páros szám.
Ezek alapján (4x2-8x+74)y2-8y+7=1 teljesül, ha
a)
4x2-8x+74=1→4x2-8x+3=0→→(2x-3)(2x-1)=0→x1=12;x2=32.
Ilyenkor persze y tetszőleges.
b) | y2-8y+7=0→(y-7)(y-1)=0→y1=1;y2=7. |
Itt kell még az is, hogy az alap nem nulla, de mivel 4x2-8x+7=4(x-1)2+3≥3, ezért ez minden x-re teljesül.
c) | 4x2-8x+74=-1→4x2-8x+11=0. |
Mivel itt D<0, ezért ilyenkor nem teljesülhet az egyenlet.
Most nézzük az arccosx=arcsiny egyenletet. Az előzőek alapján négy esetet kell megvizsgálni.
i) x=12→arccosx=π3=arcsiny→y=sin(π3)=32.
ii) x=32. Mivel arccosx értelmezési tartománya [-1;1], itt nincs megoldás.
iii) y=1→arccosx=π2=arcsin1→x=cos(π2)=0.
iv) y=7. Mivel arcsiny értelmezési tartománya [-1;1], itt sincs megoldás.
Összegezve: két számpár elégíti ki az egyenletet, (x=12;y=32), illetve (x=0; y=1).
7. Egy egyenesnek tekinthető 210 km hosszú autópálya-útszakasz mentén néhány mentőállomás áll. Az első állomás a 0-adik km-nél van, a második az első km-nél, ...; általában az i-edik, és az (i+1)-edik mentőállomás között ikm a távolság (és az állomások balról jobbra számozottak).
a) Hány mentőállomás van az út mentén?
b) Ha baleset történik valamely pontján az útszakasznak (feltehetjük, hogy a baleset bekövetkezte bármely útszakaszon a szakasz hosszával egyenesen arányos), akkor mindkét szomszédos mentőállomást értesítik, és mindkét helyről indul egy mentőkocsi. Egy perc készenlétbe állási idő után konstansnak tekinthető 60 km/h-s sebességgel száguldanak a kocsik a céljuk felé. Mekkora eséllyel ér ki a baleset helyszínére legfeljebb 4 perc alatt legalább egy mentőkocsi?
c) Az útszakasz valamely pontján mentési gyakorlatot tervez a katasztrófavédelem. Hol legyen a mentési gyakorlat, hogy a lehető legkisebb legyen a mentők benzinköltsége? (Minden állomásról egy mentőkocsi vesz részt, melyeknek azonos a fogyasztásuk.) (16 pont)
Megoldás. a) Legyen a mentőállomások száma: n, de indexeljük őket ,,furcsán'': a 0-dik mentőállomás legyen 0-nál, az első 1 km-nél, a második: 1+2 km-nél, ..., ekkor az utolsó (a furcsa indexelés miatt az) (n-1)-edik lesz az 1+2+3+...+(n-1) km-nél. Innen | 1+2+...+(n-1)=(n-1)n2=210→n1=21,n2=-20, |
vagyis 21 mentőállomás van.
b) Használjunk geometriai valószínűséget. Először is kiszámoljuk, hogy a ,,jó helyek hosszúsága'' mekkora. A szöveg alapján azokról az állomásokról ér ki a mentő a baleset helyére 4 perc alatt, ahol a távolság legfeljebb
Egészen addig, ameddig két állomás között legfeljebb 6 km a távolság, a köztük lévő helyekre kiér legalább egy mentő. Ezen helyek (az út ,,eleje'') ,,összhossza'': 1+2+3+4+5+6=21 (km), és az első 6 darab mentőállomások közötti intervallumot jelentik. Mivel 21 mentőállomáshoz 20 ilyen ,,belső intervallum'' tartozik, ezért meg kell vizsgálni a maradék 14 ilyen részt. Minden ilyen ,,nem teljesen jó'' intervallumon pontosan 6 km-nyi olyan szakasz van, ahova legalább egy mentő kiér időben, 3-3 km-nyi mindkét állomás ,,mellett''. Vagyis összességében 21+14⋅6=105 km-nyi szakaszra érnek ki időben a mentők, ez pedig a teljes útszakasz 105210=12 része, azaz a baleset helyszínére 12 eséllyel ér ki legalább egy mentőkocsi.
c) A kérdéses pont általában:
‐ páratlan mennyiségű pont (mentőállomás/számsokaság) esetén a nagyság szerint középső medián-pont;
‐ míg páros mennyiségű pont (mentőállomás/számsokaság) esetén a nagyság szerinti két középső pont közötti bármelyik pont, a medián-szakasz.
Ez a tétel például (külön páros, külön páratlan esetre) a pontok száma szerinti teljes indukcióval könnyen igazolható (ettől most eltekintünk).
Ez alapján a gyakorlatot a középső mentőállomásnál, vagyis: 1+2+...+9+10=55 km-nél érdemes megtartani.
8. a) Igazoljuk, hogy azon pontok halmaza a síkon, melyekre teljesül az (x+y)2-2(x+2)(y+1)=42, egy k kör. Mi a k kör középpontja, és sugara?
b) Az e egyenes egyenlete x+2y=10. Adjuk meg a P(1013;2016) ponton átmenő, az e egyenesre merőleges f egyenes egyenletét.
c) Válasszunk véletlenszerűen egy pontot a k kör belsejében. Mekkora a valószínűsége, hogy a kiválasztott pont közelebb van az e egyeneshez, mint az f egyeneshez?
(A k kör, e, f egyenesek a fenti pontok során definiált ponthalmazok.) (16 pont)
Megoldás. a) Átalakítva az egyenletet:
(x+y)2-2(x+2)(y+1)=42,x2+2xy+y2-2xy-2x-4y-4=16,x2-2x+1+y2-4y+4=25,(x-1)2+(y-2)2=52.
Innen a k kör középpontja O(1;2), míg sugara r=5
b) Az e:x+2y=10 egyenes egy normálvektora: ne(1;2). Ez egyúttal f irányvektora is. Innen f egy normálvektora nf(2;-1), és innen f egyenlete f:2x-y=2⋅1013-1⋅2016=10.
c) Itt is geometriai valószínűséget alkalmazunk. A kérdéses valószínűséget területek arányával számoljuk. Először nézzük meg, hol metszi az e egyenes az f-et. Megoldva az
x+2y=10,2x-y=10
egyenletrendszert: x=6; y=2. Vagyis az egyenesek metszéspontja: M(6;2). Ez éppen a k körre esik, hiszen (6-1)2+(2-2)2=25+0=52.
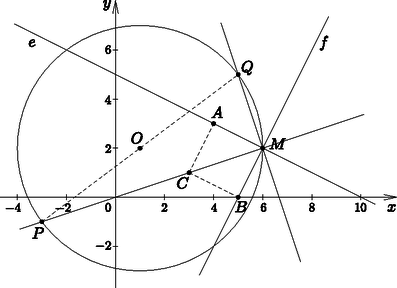
Mely pontok lesznek közelebb e-hez, mint f-hez? Használjuk az ábrát.
Az e-hez közelebbi pontokat az f-hez közelebbi pontoktól éppen a két egyenes szögfelezői választják el egymástól. e és f merőlegesek egymásra, valamint a szögfelezőik is merőlegesek egymásra.
Találjunk egy M-től különböző pontot az egyik szögfelezőn. Mivel e, és f irányvektorai: ve(-2;1), és vf(-1;-2) egyenlő hosszúak, és merőlegesek egymásra, ezért az m(6;2), m+ve, m+vf, m+ve+vf vektorok által meghatározott M(6;2), A(4;3), B(5;0), C(3;1) pontok egy négyzet csúcsai. Az A, B pontok éppen az e, illetve az f egyenesekre esnek, C pedig a szögfelezőre, vagyis az egyik szögfelező irányvektora: ve+vf=(-3;-1).
Innen az egyik szögfelező egyenlete: y=x3, (míg a másik szögfelező egyenlete (hasonlóan): y+3x=20). Ennek a szögfelezőnek a metszéspontját kiszámolva a körrel:
3y=x(x-1)2+(y-2)2=52}(3y-1)2+(y-2)2=25,9y2-6y+1+y2-4y+4=25,10y2-10y-20=0,10(y-2)(y+1)=0.
Innen adódik, hogy az M-től különböző másik metszéspont P(-3;-1). Mivel a szögfelezők merőlegesek egymásra, és metszéspontjuk a körön van, ezért PMQ háromszögnek éppen a Thalész-köre a k kör, így PQ a kör átmérője. Innen Q kordinátái: Q(5;5)
A kedvező, e egyeneshez közelebbi terület a PMQ háromszögnek, és a k kör egyik félkörének a területösszege. MQ és PM szakaszok hossza: | MQ=12+32=10,ésPM=92+32=310. |
Innen a kedvező terület: vagyis a valószínűség:
9. Az M2016-os bolygón nyolcféle űrbéli állat él. A még el nem nevezett állatokat a biológusok a latin abc A, B, C, D, E, F, G, H betűivel kódolták. Némelyik állat megeszi a másikat, hogy melyik melyiket azt a következő táblázat adja meg.
Állat A B C D E F G H ,,Zsákmánya'' B,C ‐ A,D,F F,G,H,E H,G A,B,H B,H ‐
a) A bolygóra érkező földi expedíció elfog mind a 8 állatból egy-egy példányt, és az állatokat a Földre szeretnék szállítani. Legalább hány ketrecbe zárják az állatokat, ha mindet épségben akarják hazavinni? (Egy ketrecben akárhány állat elfér.)
b) Véletlenszerűen kiválasztva két állatot a 8 közül mennyi a valószínűsége, hogy egyik sem bántja a másikat?
c) A nyolc állat felhelyezhető-e úgy egy kör alakú cirkuszi porond kerülete mentén, hogy a körvonalon szomszédos állatok ne bántsák egymást? (16 pont)
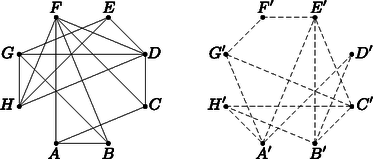
Megoldás. Használjunk gráfokat. A bal oldali ábra az állatok ,,ellenség-gráfja'', míg a jobb oldali (szaggatott éleket használva) az előző gráf komplementere, az állatok ,,barátság-gráfja''.
a) Jól látható, hogy az ellenség-gráfon található 4-elemű klikk (teljes 4-elemű részgráf) amit a D, E, G, H pontok alkotnak. Ezeket az állatokat muszáj négy különböző ketrecbe tenni. Viszont négy ketrec elég is. Például a következő elosztás jó:
első ketrec:D,A,második ketrec:E,B,C,harmadik ketrec:G,F,negyedik ketrec:H.
(Ezzel gráfnyelven azt mutattuk meg, hogy a gráf csúcs-kromatikus száma 4.)
b) Nyilván két állat akkor ,,barátságos'', ha a barát-gráfon össze vannak kötve. Mivel a 8-csúcsú teljes gráf éleinek a száma 8⋅72=28, míg a barát-gráf éleinek a száma (pl csúcsfokszámok öszegének a felét számolva) 262=13, ezért a kérdéses valószínűség: 1328.
c) Ez a kérdés gráfnyelven a barátság-gráfban egy Hamilton-körre kérdez rá. Található ilyen a barátság-gráfban (érdemes a két 2-fokszámú F, D csúcsokkal indulni, azoknak adott a két szomszédja), például az állatok egy megfelelő sorrendje a porondon: ADBHCGFE(A). |
 PDF | MathML
PDF | MathML