Cím:	Megoldásvázlatok a 2016/8. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Deák Anna
Füzet:	2016/december, 524 - 530. oldal	PDF  |  MathML
Hivatkozás(ok):	2016/november: Gyakorló feladatsor emelt szintű matematika érettségire

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Oldjuk meg az egyenleteket a valós számok halmazán: $a)$ $\sqrt[]{x+12}+\sqrt[]{x-12}=6;$ $b)$ $3^{\text{lg}{x}^2}+3^{1+\text{lg}x}=108$.  (12 pont)   Megoldás. $a)$ Az egyenlet bal oldala $x\ge$12 esetén értelmezett. Mindkét oldal nemnegatív, ezért a négyzetre emelés ekvivalens átalakítás lesz, és összevonás után a következőt adja: $\begin{array}{c}{\displaystyle 2x+2\sqrt[]{x^2-144}=36.}\end{array}$ 2-vel osztva, $x$-et kivonva, majd négyzetre emelve az $\begin{array}{c}{\displaystyle x^2-144=x^2-36x+324}\end{array}$ egyenletet kapjuk (ez csak $x\le 18$ esetén ekvivalens átalakítás). Ezt 0-ra rendezve és megoldva $x=13$ adódik eredményül, ami a kikötésnek megfelel, és az ekvivalens lépések miatt biztosan helyes gyök. $b)$ A hatványozás és a logaritmus azonosságait alkalmazva: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 3^{2\text{lg}x}+3^{1+\text{lg}x}}& {\displaystyle =\mathrm{108,}}\hfill \\ \hfill {\displaystyle {\left(3^{\text{lg}x}\right)}^2+3\cdot 3^{\text{lg}x}}& {\displaystyle =108.}\hfill \end{array}}$ $3^{\text{lg}x}$-et új változónak tekintve másodfokú egyenletet kapunk, amelyből $3^{\text{lg}x}=-12$ vagy $3^{\text{lg}x}=9$ adódik. Az első eset nem lehetséges, a másodikból $\text{lg}x=2$, azaz $x=100$, ami valóban gyöke az egyenletnek.   2. Az $\left\{1;2;3;4;\text{...};400\right\}$ számhalmaz elemei közül kiválasztunk egyet véletlenszerűen. (Mindegyiket egyenlő eséllyel.) Mekkora a következő események valószínűsége: $a)$ A húzott szám osztható $3$-mal, de nem osztható $4$-gyel; $b)$ A húzott szám osztható $3$-mal, $4$-gyel vagy $5$-tel; $c)$ A húzott szám számjegyeinek összege $5?$  (14 pont)   Megoldás. $a)$ 3-mal osztható 133 db szám, ezek közül 4-gyel is osztható 33 db szám (a 12 többszörösei), vagyis a kedvező esetek száma 100, a valószínűség $\frac{100}{400}=0\mathrm{,}25$. $b)$ 3-mal 133 db, 4-gyel 100 db, 5-tel 80 db, 12-vel 33 db, 15-tel 26 db, 20-szal 20 db, 60-nal 6 db szám osztható. A kedvező esetek száma: $133+100+80-33-26-20+6=240$, a valószínűség $\frac{240}{400}=0\mathrm{,}6$. $c)$ A megfelelő háromjegyű számok: 140, 104, 230, 203, 320, 302, 221, 212, 122, 113, 131, 311; kétjegyűek: 14, 41, 23, 32, 50, egyjegyű: 5. A kedvező esetek száma 18, a valószínűség $\frac{18}{400}=0\mathrm{,}045$.   3. 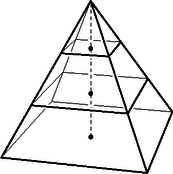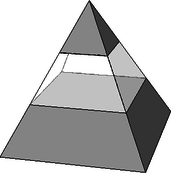$a)$ Egy szabályos négyoldalú gúlát az alaplappal párhuzamos, a magasság harmadolópontjain átfektetett két síkkal három részre osztunk. A középső, csonkagúla alakú rész térfogata $28\text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msup><mrow><mi>m</mi></mrow><mrow><mn>3</mn></mrow></msup></mrow></math>}$. Számítsuk ki a teljes gúla térfogatát.     $b)$ Az előbbi gúla egy köztéri alkotásnak szánt kisebb épület, alapéle 6 m. Felszínét a középső részen üveg borítja. Mekkora az üvegezett felület?  (14 pont)       Megoldás. $a)$ A három gúla hasonló, hasonlóságuk aránya $1:2:3$, ebből térfogatuk aránya $1:8:27$, a középső csonkagúla térfogata $\frac{8}{27}-\frac{1}{27}=\frac{7}{27}$ része a gúla térfogatának, és ez 28 cm${}^3$. Ebből a gúla térfogata 108 cm${}^3$. $b)$ A gúla alaplapjának területe 36 m${}^2$. A gúla térfogatképletéből a magasságra 9 méter adódik. 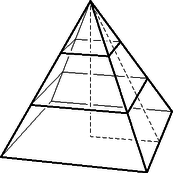Az ábrán szaggatott vonallal rajzolt derékszögű háromszögre a Pitagorasz-tételt felírva az oldallap magasságára $\sqrt[]{90}$ métert kapunk.     A párhuzamos szelők tétele alapján a csonkagúlát határoló trapéz magassága ennek harmadrésze, azaz $\sqrt[]{10}$ méter. A trapéz két alapja 2 m és 4 m, területe az előbbi adatokból $3\sqrt[]{10}{\text{m}}^2$. Az üvegezett felület ennek 4-szerese, azaz $\begin{array}{c}{\displaystyle 12\sqrt[]{10}{\text{m}}^2\approx 37\mathrm{,}95{\text{m}}^2\mathrm{.}}\end{array}$   4. Egy hat elemű adathalmaz átlaga $10$. Az első négy adat: $6$, $11$, $14$, $8$. $a)$ Mennyi a hiányzó két adat átlaga? $b)$ Adjuk meg a hiányzó két adatot, ha az adathalmaz szórása $\sqrt[]{7}$.  (12 pont)   Megoldás. $a)$ A hat adat összege 60, tehát a két hiányzó adat összege 21, átlaguk 10,5. $b)$ Legyen a két adat $x$ és $y$. Tudjuk, hogy $x+y=21$. A szórás: $\begin{array}{c}{\displaystyle \sqrt[]{\frac{{\left(6-10\right)}^2+{\left(11-10\right)}^2+{\left(14-10\right)}^2+{\left(8-10\right)}^2+{\left(x-10\right)}^2+{\left(y-10\right)}^2}{6}}=\sqrt[]{7}\mathrm{.}}\end{array}$ $y$ helyébe $\left(21-x\right)$-et írva: $\begin{array}{c}{\displaystyle \sqrt[]{\frac{16+1+16+4+{\left(x-10\right)}^2+{\left(11-x\right)}^2}{6}}=\sqrt[]{7}\mathrm{.}}\end{array}$ Négyzetre emelve és rendezve az $x^2-21x+108=0$ egyenletre jutunk, melynek gyökei 12 és 9. Tehát $x=12$, $y=9$, vagy fordítva. A két hiányzó adat tehát 9 és 12.   II. rész     5. Egy társasjáték kelléke $80$ darab kártyalap, amelyeken kék vagy piros színnel egy-egy írásjel látható. A jelek $30\%$-a kérdőjel, $45\%$-a felkiáltójel, a többi pont. A piros írásjeleknek $3/8$ része, a kékeknek $1/6$ része pont. $a)$ Hány kék, illetve piros lap van a pakliban? Ha a játék során tíz alkalommal húzok a pakliból (a húzott lapokat mindig visszatesszük, és újrakeverjük a kártyákat), mekkora a valószínűsége, hogy $b)$ egy kérdőjelet sem húzok; $c)$ $3$-nál több kérdőjelet húzok? $d)$ Mennyi a húzott kérdőjelek számának várható értéke?  (16 pont)   Megoldás. $a)$ 24 kérdőjel, 36 felkiáltójel, és így 20 pont van a jelek között. Ha a pirosak számát $n$-nel, a kékekét $\left(80-n\right)$-nel jelöljük, a pontok száma $\begin{array}{c}{\displaystyle \frac{3}{8}n+\frac{1}{6}\left(80-n\right)=20.}\end{array}$ Ezt megoldva azt kapjuk, hogy 32 piros és 48 kék lap van a pakliban. $b)$ Egy húzás alkalmával 0,3 valószínűséggel húzok kérdőjelet, 0,7 valószínűséggel mást. Annak valószínűsége, hogy a tíz húzásból egy sem kérdőjel $0\mathrm{,}{7}^{10}\approx 0\mathrm{,}028$. $c)$ Jelölje $p\left(n\right)$ annak valószínűségét, hogy a kérdőjelek száma $n$. Ekkor $p\left(0\right)=0\mathrm{,}028$; $p\left(1\right)=10\cdot 0\mathrm{,}3\cdot 0\mathrm{,}{7}^9\approx 0\mathrm{,}121$; $p\left(2\right)=\left(\genfrac{}{}{0ex}{}{10}{2}\right)\cdot 0\mathrm{,}{3}^2\cdot 0\mathrm{,}{7}^8\approx 0\mathrm{,}233$; $p\left(3\right)=\left(\genfrac{}{}{0ex}{}{10}{3}\right)\cdot 0\mathrm{,}{3}^3\cdot 0\mathrm{,}{7}^7\approx 0\mathrm{,}267$. Ezeket az értékeket összeadva annak valószínűsége, hogy legfeljebb 3 kérdőjelet húzunk 0,649. Annak valószínűsége, hogy ennél több kérdőjelet húzunk $1-0\mathrm{,}649=0\mathrm{,}351$. $d)$ Binomiális eloszlásról van szó, melynek paramétere 0,3, a kísérletek száma 10. A várható érték $n\cdot p=10\cdot 0\mathrm{,}3=3$.   6. $a)$ $\left(a_n\right)$ és $\left(b_n\right)$ pozitív tagú mértani sorozatok, hányadosuk $1\mathrm{,}5$, illetve $2$. Állapítsuk meg az alábbi sorozatokról, hogy mértani sorozatok, illetve számtani sorozatok-e, és ha igen, adjuk meg a hányadost $\left(q\right)$, illetve a differenciát $\left(d\right)$.     $b)$ A fent említett $\left(a_n\right)$ sorozat első tagja $0\mathrm{,}2$. Számítsuk ki az $\begin{array}{c}{\displaystyle \frac{1}{a_1}+\frac{1}{a_{n+1}}+\frac{1}{a_{n+2}}+\frac{1}{a_{n+3}}+\text{...}}\end{array}$ végtelen sor összegének pontos értékét. $c)$ Egy nyolctagú számtani sorozat páratlan indexű tagjainak összege $8\mathrm{,}8$, páros indexű tagjainak összege $10\mathrm{,}4$. Adjuk meg a nyolc tagot.  (16 pont)   Megoldás. $a)$     $b)$ A sor első tagja 5, hányadosa 1,5-nek reciproka, azaz $\frac{2}{3}$. Az összeg: $\begin{array}{c}{\displaystyle \frac{5}{1-\frac{2}{3}}=15.}\end{array}$ $c)$ ${\displaystyle \begin{array}{cc}{\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>2</mn><mi>d</mi><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>4</mn><mi>d</mi><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>6</mn><mi>d</mi><mo stretchy="false">=</mo><mn>8</mn><mn>,</mn><mn>8</mn></math>, }}\hfill & {\displaystyle \text{ ebből <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>12</mn><mi>d</mi><mo stretchy="false">=</mo><mn>8</mn><mn>,</mn><mn>8</mn></math>.}}\hfill \\ {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mi>d</mi><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>3</mn><mi>d</mi><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>5</mn><mi>d</mi><mo stretchy="false">+</mo><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>7</mn><mi>d</mi><mo stretchy="false">=</mo><mn>10</mn><mn>,</mn><mn>4</mn></math>, }}\hfill & {\displaystyle \text{ ebből <math xmlns="http://www.w3.org/1998/Math/MathML"><mn>4</mn><mrow><msub><mrow><mi>a</mi></mrow><mrow><mn>1</mn></mrow></msub></mrow><mo stretchy="false">+</mo><mn>16</mn><mi>d</mi><mo stretchy="false">=</mo><mn>10</mn><mn>,</mn><mn>4</mn></math>. }}\hfill \end{array}}$ Az egyenletrendszer megoldása $d=0\mathrm{,}4$, $a_1=1$. A tagok: 1; 1,4; 1,8; 2,2; 2,6; 3; 3,4; 3,8.   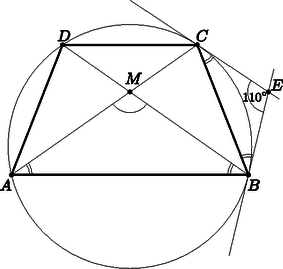7. $a)$ $ABCD$ húrtrapéz, hosszabbik alapja az $AB$ oldal. A trapéz köré írt körhöz érintőt húzunk a $B$ és a $C$ csúcsban, a metszéspontot $E$-vel jelölve $CEB\sphericalangle ={110}^{\circ }$. Milyen szögben metszik egymást a trapéz átlói? 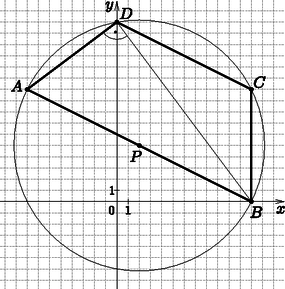$b)$ $ABCD$ húrtrapéz, hosszabbik alapja az $AB$ oldal, $A\left(-8;10\right)$, $B\left(12;0\right)$. Tudjuk továbbá, hogy a $D$ csúcs az $y$ tengely pozitív félegyenesére illeszkedik, és az átlók merőlegesek egy-egy szárra. Határozzuk meg a $C$ és a $D$ csúcs koordinátáit.  (16 pont)   Megoldás. $a)$ Legyen $M$ az átlók metszéspontja. $ECB\sphericalangle$ és $EBC\sphericalangle$ a kör $BC$ húrjához tartozó érintőszárú kerületi szögek, tehát egyenlők, és a nagyságuk ${35}^{\circ }$. $CAB\sphericalangle$ ugyanahhoz a húrhoz tartozó kerületi szög, ezért egyenlő az előbbiekkel, vagyis ${35}^{\circ }$. A szimmetria miatt a $DBA\sphericalangle$ is ${35}^{\circ }$. Az $AMB$ háromszögben a harmadik szög ${110}^{\circ }$, tehát az átlók által közbezárt szög ${180}^{\circ }-{110}^{\circ }={70}^{\circ }$.     $b)$ Mivel a $D$ csúcsból az $AB$ alap derékszögben látszik, $D$ rajta van az $AB$ szakasz Thalész-körén. Ennek középpontja $P\left(2;5\right)$, sugara Pitagorasz tételéből $\sqrt[]{125}$. A kör egyenlete $\begin{array}{c}{\displaystyle {\left(x-2\right)}^2+{\left(y-5\right)}^2=125.}\end{array}$ A $D$ pont 1. koordinátája 0, ezt $x$ helyébe írva és az egyenletet $y$-ra megoldva $y=16$ és $y=-6$ adódik. A szöveg szerint csak $y=16$ helyes, tehát $D\left(0;16\right)$.     A $DC$ szakasz párhuzamos az $AB$ szakasszal, ezért irányvektoruk megegyezik. $\overrightarrow{AB}\left(20;-10\right)$, ezt 10-zel osztva egy egyszerűbb irányvektor $\text{v}\left(2;-1\right)$. Ebből a $DC$ egyenes normálvektora $\text{n}\left(1;2\right)$, ismert pontja $D\left(0;16\right)$. Írjuk fel az egyenletét: $x+2y=32$. Oldjuk meg az egyenes és a kör egyenletéből álló egyenletrendszert. $x=0$, $y=16$, illetve $x=12$, $y=10$ a két megoldás, vagyis $C\left(12;10\right)$.   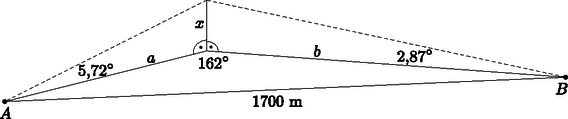8. $a)$ Egy síkságon futó egyenes vasúti szakasz két állomásépületének távolsága 1,7 km. A vasútvonaltól távolabb álló toronyház teteje az egyik állomásról $5\mathrm{,}{72}^{\circ }$-os, a másikról $2\mathrm{,}{87}^{\circ }$-os emelkedési szögben látszik. A torony tövénél állva a két állomás közötti szakasz ${162}^{\circ }$-os szögben látható. Készítsünk ábrát. Adjuk meg a torony magasságát egész méterre kerekítve. $b)$ Egy háromszög két oldala 70 m és 110 m, a velük szemközti szögek különbsége ${30}^{\circ }$. Mekkorák a háromszög szögei? (Az eredményeket egy tizedesjegy pontossággal adjuk meg.)  (16 pont)   Megoldás. $a)$ Az ábrán $A$ és $B$ az állomásokat jelöli. A torony magassága legyen $x$. A két derékszögű háromszögben $a$-t és $b$-t kifejezve $\begin{array}{c}{\displaystyle a=\frac{x}{\text{tg}5\mathrm{,}{72}^0}=\frac{x}{0\mathrm{,}1}\text{és}b=\frac{x}{\text{tg}2\mathrm{,}{87}^0}=\frac{x}{0\mathrm{,}05}\mathrm{.}}\end{array}$     A torony töve és az állomások által meghatározott háromszögre írjuk fel a koszinusztételt: $\begin{array}{c}{\displaystyle {1700}^2=a^2+b^2-2ab\cdot \text{cos}{162}^{\circ }\mathrm{.}}\end{array}$ $a$ és $b$ helyébe a fenti kifejezéseket behelyettesítve olyan egyenletet kapunk, amelynek a változója az $x$. Ezt megoldva az eredmény $x=57\mathrm{,}29$ m. A torony magassága méterre kerekítve 57 m. $b)$ A 70 m-es oldallal szemközti szög legyen $\alpha$, a 110 m-es oldallal szemközti szög $\alpha +{30}^{\circ }$. (A nagyobb oldallal szemben van a nagyobb szög.) A szinusztétel szerint $\begin{array}{c}{\displaystyle \frac{\text{sin}\left(\alpha +{30}^{\circ }\right)}{\text{sin}\alpha }=\frac{11}{7}\mathrm{.}}\end{array}$ Szorozzunk be $\text{sin}\alpha$-val, a baloldalon alkalmazzunk addíciós tételt, a tört, illetve gyök alakban adott értékeket írjuk át tizedestörtbe: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 0\mathrm{,}866\text{sin}\alpha +0\mathrm{,}5\text{cos}\alpha }& {\displaystyle =1\mathrm{,}5714\text{sin}\alpha \mathrm{,}}\hfill \\ \hfill {\displaystyle 0\mathrm{,}5\text{cos}\alpha }& {\displaystyle =0\mathrm{,}7054\text{sin}\alpha \mathrm{.}}\hfill \end{array}}$ Osszuk az egyenlet két oldalát $\text{cos}\alpha$-val (ami nem 0, mert $\alpha ={90}^{\circ }$-ra nem igaz az egyenlet): $\begin{array}{c}{\displaystyle 0\mathrm{,}70887=\text{tg}\alpha \mathrm{.}}\end{array}$ Ebből $\alpha =35\mathrm{,}{3}^{\circ }$, $\alpha +{30}^{\circ }=65\mathrm{,}{3}^{\circ }$, a harmadik szög $79\mathrm{,}{4}^{\circ }$.   9. $a)$ Adjuk meg az $f$ harmadfokú függvényt, ha egyik zérushelye az $1$, deriváltja az $f\text{'}\left(x\right)=3x^2-12x+11$ függvény. $b)$ Jelölje $p$ a $g\left(x\right)=\text{sin}\frac{x}{3}$ függvény legkisebb pozitív zérushelyét. Számítsuk ki a $\left[0;p\right]$ intervallumon a $g$ függvény grafikonja és az $x$ tengely közé eső zárt területet. 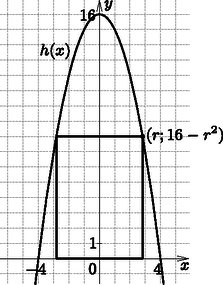$c)$ A $h\left(x\right)=-x^2+16$ függvény grafikonja és az $x$ tengely által határolt síkidomot megforgatjuk az $y$ tengely körül. Mekkora az így kapott forgástestbe írható maximális térfogatú henger térfogata?  (16 pont)   Megoldás. $a)$ $f\left(x\right)$ az $f\text{'}\left(x\right)$ primitívfüggvénye, tehát $f\left(x\right)=x^3-6x^2+11x+c$. Tudjuk, hogy $f\left(1\right)=0$, tehát $0=1-6+11+c$, amiből $c=-6$. A függvény hozzárendelési szabálya $f\left(x\right)=x^3-6x^2+11x-6$. $b)$ $\text{sin}\frac{x}{3}=0$ akkor és csak akkor, ha $\frac{x}{3}=k\pi$, vagyis $x=3k\pi$ ($k$ egész). A legkisebb pozitív zérushely tehát a $3\pi$. A $\left[0;3\pi \right]$ intervallumon a függvény értékei pozitívak, ezért az $x$-tengellyel bezárt terület $\begin{array}{c}{\displaystyle \underset{0}{\overset{3\pi }{\int }}\text{sin}\frac{x}{3}={\left[-3\text{cos}\frac{x}{3}\right]}_0^{3\pi }=3-\left(-3\right)=6.}\end{array}$ $c)$ A forgástestnek és a beírt hengernek a koordinátasíkra eső keresztmetszetét mutatja az ábra.     A henger alapkörének sugara $r$, magassága $16-r^2$. Ebből a térfogata $\begin{array}{c}{\displaystyle V=r^2\left(16-r^2\right)\pi \mathrm{.}}\end{array}$ Ez akkor maximális, ha $\begin{array}{c}{\displaystyle f\left(r\right)=r^2\left(16-r^2\right)=16r^2-r^4}\end{array}$ maximális, ahol $0<r<4$. A függvény deriváltja $\begin{array}{c}{\displaystyle f\text{'}\left(r\right)=32r-4r^3=4r\left(8-r^2\right)\mathrm{.}}\end{array}$ A vizsgált tartományban a derivált értéke 0, ha $r=\sqrt[]{8}$, pozitív, ha $r<\sqrt[]{8}$ és negatív, ha $r>\sqrt[]{8}$. A $\left]0;4\right[$ intervallumon tehát az $f\left(r\right)$ függvénynek a $\sqrt[]{8}$-ban maximuma van. A henger maximális térfogata így $V=8\cdot \left(16-8\right)=64$.