Cím: Visszalépéses keresés
Szerző(k):  Schmieder László 
Füzet: 2016/november, 482 - 484. oldal  PDF  |  MathML 
Hivatkozás(ok):2017/január: Visszalépéses keresés 2.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Amikor számítógéppel keressük egy kombinatorika probléma megoldását, akkor előfordul, hogy a végeredmény megtalálásához az összes lehetséges esetet meg kell vizsgálnunk. Ha az esetek száma kevés, akkor papíron is végignézhetjük azokat, de ha számuk elég nagy, akkor használjunk inkább számítógépet. A visszalépéses keresés algoritmusa lényegében az összes, bizonyos feltételnek eleget tevő eset logikus sorrendben történő vizsgálatát jelenti. Az algoritmus a jól ismert 8 vezér problémával nagyon szemléletesen bemutatható. A feladat: helyezzünk el a sakktáblán 8 vezért úgy, hogy azok ne üssék egymást.
Nézzük, hogyan csinálnánk papíron: elhelyezünk néhány vezért az első három-négy oszlopba, majd az ötödiknél már körültekintőbben járunk el, de a hetedik és nyolcadik vezér lerakása valahogy mégsem sikerül. Látjuk, hogy egy korábbi döntésünk során elhelyezett vezér akadályoz minket a továbblépésben, ezért egy már elhelyezett vezért kell egy másik mezőre helyeznünk. Ezután újra próbálkozhatunk újabb vezér elhelyezésével.

 
 

Nyilvánvalóan látszik, hogy akkor van esélyünk megoldani a problémát, ha minden vezérnek saját oszlopa és sora van. Ha tudatosan és módszeresen szeretnénk végigjárni az eseteket, akkor minden oszlophoz rendeljünk egy vezért. Az első vezért tegyük az első oszlop első sorába. A második kerüljön a második oszlopba úgy, hogy ne üsse az elsőt. A harmadik vezér kerüljön a harmadik oszlopba úgy, hogy ne üsse az előző kettőt. Így mehetünk előre, amíg el tudunk helyezni a következő oszlopba vezért. Ha már nem sikerül, akkor vissza kell lépnünk egy korábbi döntésünkhöz. Tegyük ezt úgy, hogy az előző oszlopban mozgatjuk a következő megfelelő helyre a már elhelyezett vezért. Ha sikerül, akkor folytatjuk azzal az oszloppal, ahonnan visszaléptünk. Ha nem sikerül, akkor még korábbi oszlopba kell visszalépnünk, hogy az oda elhelyezett vezért mozgassunk megfelelőbb helyre. Ilyenkor természetesen az utána következő vezéreket levesszük.
A fenti algoritmus kétféleképp fejeződhet be: vagy sikerül mind a 8 oszlopban elhelyezni a vezéreket, ekkor találtunk egy megoldást; vagy az első oszlop 8-adik sorában álló vezérhez sem tudunk megfelelő mezőt találni, és ekkor nincs a feladatnak megoldása.
A módszerünk adatokkal úgy fejezhető ki, hogy minden oszlophoz hozzárendeljük a benne álló vezér sorszámát. Ekkor a feladat annak a 8 elemű v vektornak a megkeresése, amely megadja, hogy az egyes oszlopokon belül melyik sorban áll a vezér. Például a fenti ábra megfelelője a [2,4,1,7,5,0,0,0], ahol a zérus értékek azt jelölik, hogy abban az oszlopban még nem áll vezér. A kiinduló állás esetén v értéke nyilván [0,0,0,0,0,0,0,0], ami jelentse azt, hogy a vezérek az adott oszlopban az első sor előtt, a tábla szélén állnak. A visszalépéses keresés (backtrack) algoritmusa a 8 vezér elhelyezésére tehát a következő:
 

Eljárás Backtrack(v)
    v[] := 0
    oszlop := 1
    Ciklus amíg 1<=oszlop és oszlop<=8
        Ciklus
            v[oszlop] := v[oszlop]+1
        Ciklus amíg v[oszlop]<=8 és Ütésben(oszlop)
        Ha v[oszlop]<=8 akkor
            oszlop := oszlop+1
        egyébként
            v[oszlop] := 0
            oszlop := oszlop-1
        Elágazás Vége
    Ciklus Vége
Eljárás Vége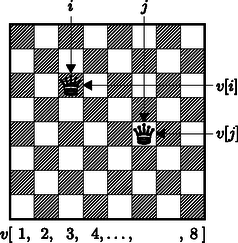
 
Az eljárás pontosan azt valósítja meg, amit korábban leírtunk. A belső ciklus megkeresi az adott oszlopban a következő lehetséges sort a vezér számára: addig lép további mezőkre, amíg az adott mező ütésben van. Ha találunk megfelelő mezőt, akkor a ciklus után a következő oszloppal folytatjuk a keresést, míg ha nem, akkor az adott oszlop vezérét levesszük, és az előző oszlopban álló vezérnek keresünk helyet. Az algoritmus befejeződésekor az oszlop változó értéke mutatja, hogy sikerült-e megoldást találnunk: zérus esetén nincs megoldás, míg a 9 jelenti azt, hogy a v tömb jelenleg egy jó elrendezést tartalmaz.

 
 

Ha a vezérek nem ütik egymást, akkor nincsenek azonos sorban, és azonos átlóban. Ez a két feltétel a következő matematikai alakban fejezhető ki: minden 1≤i,j≤8 oszlop esetén v[i]≠v[j] és |i-j|≠|v[i]-v[j]|.
Ezek szerint az Ütésben() függvénynek nem kell mást tennie, mint megvizsgálnia, hogy az előző oszlopokban álló vezérek közül üti-e valamelyik a most elhelyezett vezért.
 

Függvény Ütésben(akt):Logikai
    elo := 1
    Ciklus amíg elo<akt és v[elo]<>v[akt] és |elo-akt|<>|v[elo]-v[akt]|
        elo := elo+1
    Ciklus Vége
    Függvényérték := elo<akt
Függvény Vége
 

Kérdések és feladatok:
1. Bővítsük úgy az algoritmust az oszlop változó fölhasználásával, hogy az összes lehetséges megoldást megtalálja.
2. Bővítsük úgy az algoritmust, hogy megadja azokat az n számokat, amelyek esetében megoldható az n vezér probléma (n vezér egy n×n méretű sakktáblán).
3. Az eddigiek alapján hasznos gyakorlat lehet még a https://mester.inf.elte.hu/ oldalon elérhető feladatok közül a Haladó ‐ Visszalépéses keresés kategóriában pl. a Sudoku1, Sudoku2 vagy az Üzletek probléma.
 

Nézzük meg a megoldásunk hatékonyságát. Ha a 2. feladat programját futtatjuk, akkor észrevehetjük, hogy 20-nál nagyobb n esetén a program rendkívül hosszú ideig fut. Ez érthető, hiszen egy n×n-es sakktáblán mindegyik oszlopban n mező van, tehát az n vezérnek nn számú különböző elhelyezése lehetséges. Ha nincs megoldás, akkor az algoritmus lényegében ennyi esetet vizsgál meg. Ha n értéke egy kisebb kétjegyű szám, akkor egy mai személyi számítógépen még kivárható időn belül lefut a keresés, de nagyobb n-ekre már nem. A visszalépéses keresést tehát csak akkor érdemes alkalmazni, ha a probléma korlátai alapján megbecsülhető esetszám nem túl nagy. Összetett feladatoknál igyekeznek az esetek számát csökkenteni, illetve eleve elhagyni azokat az eseteket, amiket nem érdemes vizsgálni, ahogy ezt mi is tettük, amikor a vezéreket külön-külön oszlopokba helyeztük el.