Cím:	Megoldásvázlatok a 2016/7. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Árokszállási Tibor ,  Faragó András ,  Káspári Tamás
Füzet:	2016/november, 464 - 471. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $2015$-ben az Energetikai Szakközépiskola és Kollégium (ESZI) végzős, $12$. osztályos százhuszonöt diákja közül néhányan emelt szintű érettségit tettek matematikából, átlaguk pontosan $3\mathrm{,}8$ volt. A többi diák középszinten érettségizett, az ő érettségi átlaguk pedig pontosan $3\mathrm{,}55$ volt. A diákok közül mindenki sikeres vizsgát tett, az összesített iskolai matematika érettségi átlag pontosan $3\mathrm{,}56$ lett. $a)$ Hányan érettségiztek emelt szinten? $b)$ Az emelt szinten érettségizők osztályzatainak mediánja: $4$, mennyi lehet az osztályzatok módusza? $c)$ Öt $13$. évfolyamos ESZI-s diák írt szintemelő érettségi dolgozatot matematikából, az ő átlaguk is $3\mathrm{,}80$ volt, és itt sem bukott meg senki. Tudjuk, hogy az osztályzataik módusza és mediánja is $5$. Mennyi a valószínűsége annak, hogy a dolgozatok közül kettőt véletlenszerűen kiválasztva közülük mindkettő jeles?  (12 pont)   Megoldás. $a)$ $x$ diák érettségizett emelt szinten és $125-x$ közép szinten. Felírjuk az alábbi egyenletet: $\begin{array}{c}{\displaystyle 3\mathrm{,}8x+3\mathrm{,}55\cdot \left(125-x\right)=3\mathrm{,}56\cdot 125.}\end{array}$ Ennek a megoldása $x=5$. Így 5 diák érettségizett emelt szinten. $b)$ Mivel a középső osztályzat 4, és a számjegyek összege $3\mathrm{,}8\cdot 5=19$, a lehetséges számötösök a következők: ${\displaystyle \begin{array}{cccc}\hfill {\displaystyle 1.}& {\displaystyle \mathrm{2,3,4,5,5};}\hfill & {\displaystyle 2.}\hfill & \hfill {\displaystyle \mathrm{2,4,4,4,5};}\\ \hfill {\displaystyle 3.}& {\displaystyle \mathrm{3,3,4,4,5};}\hfill & {\displaystyle 4.}\hfill & \hfill {\displaystyle \mathrm{3,4,4,4,4.}}\end{array}}$ Ebből a lehetséges móduszok: az első esetben 5, a második és az utolsó esetben 4, a harmadik esetben pedig 3 és 4. $c)$ Az egyetlen lehetséges számötös: 2, 2, 5, 5, 5, így az összes eset: $\left(\genfrac{}{}{0ex}{}{5}{2}\right)=10$, a kedvező esetek száma: $\left(\genfrac{}{}{0ex}{}{3}{2}\right)=3$. A valószínűségre $\frac{3}{10}$ adódik.   2. Egy számtani és egy mértani sorozat első tagja egyaránt $2$. A sorozatok második tagjai szintén egyenlők, valamint a mértani sorozat hányadosa egyenlő a számtani sorozat differenciájával. $a)$ A mértani sorozat $10$. tagja a számtani sorozat hányadik tagjával egyenlő? $b)$ Mutassuk meg, hogy a mértani sorozat bármely tagja eleme a számtani sorozatnak. $c)$ Mutassuk meg, hogy a mértani sorozat egyik tagja sem állítható elő a számtani sorozat néhány egymás utáni tagjának összegeként.  (13 pont)   Megoldás. $a)$ A sorozatok megfelelő tagjai: 2, $2+d$ és 2, $2d$, amiből $2+d=2d$, megoldása $d=2$. Tehát a számtani sorozat: $\mathrm{2,4,6,8,}\text{...}\mathrm{,}$ a mértani sorozat: $\mathrm{2,4,8,16,}\text{...}\mathrm{.}$ Így a mértani sorozat 10. tagja $2^{10}=1024$, ami a számtani sorozat 512. tagja. $b)$ A mértani sorozat a $2^n$ sorozat, így minden tagja páros szám. A számtani sorozat az $a_n=2n$ sorozat, melynek tagjai között az összes pozitív páros szám szerepel, tehát valóban eleme a mértani sorozat összes tagja. $c)$ A mértani sorozat $n$. tagja: $a_n=2^n$, a számtani sorozat néhány egymás utáni tagjának összege: $2k+\left(2k+2\right)+\text{...}+\left(2k+2\left(m-1\right)\right)$, ahol $2k$ az első összeadandó tag és $m$ a tagok száma. Így az összeg: $S=\left(4k+2\left(m-1\right)\right)\cdot \frac{m}{2}=\left(2k+m-1\right)\cdot m$. Ez utóbbi egy páratlan és egy páros szám szorzata, hiszen $m$ és $m-1$ paritása különböző. Ez csak a $2^n=1\cdot 2^n$ felbontás esetén lehetséges, de ekkor $m=1$, ami nem felel meg a feltételeknek.   3. Legyen az $f:\text{R}\to \text{R}$ függvény hozzárendelési szabálya $\begin{array}{c}{\displaystyle f\left(x\right)=4^x+0\mathrm{,}{5}^{2x}-3.}\end{array}$ $a)$ Adjuk meg az $f$ függvény értékkészletét és zérushelyeinek pontos értékét. $b)$ Mutassuk meg, hogy a függvény páros és szigorúan monoton növekvő a pozitív számok halmazán.  (13 pont)   Megoldás. $a)$ Az értékkészlethez elég a $4^x+0\mathrm{,}{5}^{2x}$ kifejezést vizsgálnunk. Ezt átalakítva $\left(4^x+\frac{1}{4^x}\right)$-t kapunk, ami legalább 2, hiszen egy pozitív szám és a reciprokának az összege. A függvény értékkészletét a $-1$-nél nem kisebb számok alkotják, mert folytonos függvények összege is folytonos, illetve a négyes alapú exponenciális függvény folytonos és szigorúan monoton növekvő, és $4^x+\frac{1}{4^x}>4^x$. A zérushely megállapításához a $4^x+0\mathrm{,}{5}^{2x}-3=0$, vagyis a $4^x+\frac{1}{4^x}-3=0$ egyenletet kell megoldanunk. Beszorozva és rendezve az egyenletet: ${\left(4^x\right)}^2-3\cdot 4^x+1=0$. A másodfokú egyenletet megoldva a megoldások: $4^x=\frac{3\pm \sqrt[]{5}}{2}$, amiből a két gyök pontos értéke: $x_1=\text{log}{}_4\frac{3+\sqrt[]{5}}{2}$, illetve $x_2=\text{log}{}_4\frac{3-\sqrt[]{5}}{2}$. $b)$ Mivel $4^x+\frac{1}{4^x}=\frac{1}{4^{-x}}+4^{-x}$, ezért a függvény páros. A szigorú monoton növekedés vizsgálatához képezzük a következő különbséget: $\begin{array}{c}{\displaystyle f\left(x+k\right)-f\left(x\right)=4^{x+k}+\frac{1}{4^{x+k}}-4^x-\frac{1}{4^x}\mathrm{,}}\end{array}$ ahol $x\ge 0$, $k>0$. Átalakítva: $\begin{array}{c}{\displaystyle 4^k\cdot 4^x+\frac{1}{4^k\cdot 4^x}-4^x-\frac{1}{4^x}=\left(4^k-1\right)4^x-\left(4^k-1\right)\frac{1}{4^k\cdot 4^x}\mathrm{.}}\end{array}$ Szorzattá alakítunk: $\begin{array}{c}{\displaystyle \left(4^k-1\right)\left(4^x-\frac{1}{4^k\cdot 4^x}\right)>\mathrm{0,}}\end{array}$ mert mindkét tényező pozitív. Ezzel bebizonyítottuk, hogy $f\left(x+k\right)-f\left(x\right)>0$, ami a szigorú monoton növekedést jelenti.   4. $a)$ Mekkora lehet a $p$ valós paraméter értéke, ha tudjuk, hogy a $\text{cos}x-\text{sin}x=p$ egyenletnek van megoldása? $b)$ Oldjuk meg az alábbi egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle \frac{2\text{cos}x+4\text{sin}x}{\text{cos}x+\text{sin}x}=2\text{tg}x+1.}\end{array}$ (13 pont)   Megoldás. $a)$ Szorozzuk az egyenletet $\frac{\sqrt[]{2}}{2}$-vel, ekkor a $\begin{array}{c}{\displaystyle \frac{\sqrt[]{2}}{2}\text{cos}x-\frac{\sqrt[]{2}}{2}\text{sin}x=p\cdot \frac{\sqrt[]{2}}{2}}\end{array}$ egyenletet kapjuk, ahol a bal oldal $\text{cos}\left(x+\frac{\pi }{4}\right)$, a jobb oldal $p\frac{\sqrt[]{2}}{2}$, aminek az értéke $-1$ és 1 közé kell, hogy essen. Ebből $-\sqrt[]{2}\le p\le \sqrt[]{2}$ adódik. $b)$ Kikötések: $\text{cos}x\ne 0$, $x\ne \frac{\pi }{2}+k\pi$ ($k\in \text{Z}$); $\text{cos}x+\text{sin}x\ne 0$, amiből $\text{tg}x\ne -1$, $x\ne \frac{3\pi }{4}+l\pi$ ($l\in \text{Z}$). Gyökvesztés nélkül egyszerűsíthetjük a bal oldalt $\text{cos}x$-szel, ekkor $\begin{array}{c}{\displaystyle \frac{2+4\text{tg}x}{1+\text{tg}x}=2\text{tg}x+1.}\end{array}$ Szorzás és rendezés után kapjuk a  $\begin{array}{c}{\displaystyle 2\text{tg}{}^{2}x-\text{tg}x-1=0}\end{array}$ másodfokú egyenletet, aminek megoldásai $\text{tg}x=1$, illetve $\text{tg}x=-\frac{1}{2}$, amiből $x=\frac{\pi }{4}+m\pi$ ($m\in \text{Z}$), illetve $x=-0\mathrm{,}46+n\pi$ ($n\in \text{Z}$) következik (ahol a $-0\mathrm{,}46$ az $\text{arctan}-\frac{1}{2}$ két tizedesjegyre kerekített értéke).   II. rész     5. Anna és Balázs szeretnek sakkozni, ezért $100$ játszmás páros mérkőzéseket szoktak játszani. Egy játszmának háromféle kimenetele lehet: $A=\{$Anna nyer$\}$, $B=\{$Balázs nyer$\}$, $C=\{$a játszma döntetlenül végződik$\}$. Tegyük fel, hogy az $A$ és a $B$ események valószínűsége a páros mérkőzések során: $P\left(A\right)=\frac{3}{5}p$, $P\left(B\right)={\left(p+\frac{1}{5}\right)}^2$, ahol $p$ valós paraméter. Anna és Balázs azt tervezik, hogy a következő hétvégén $100$ játszmás páros mérkőzést játszanak. Egy játszmában a győzelemért egy pont, a döntetlenért fél pont jár, a vereségért a játékos nem kap pontot. $a)$ Mekkora lehet a $p$ paraméter értéke? $b)$ A $p$ paraméter értékétől függően legalább, illetve legfeljebb mekkora lehet a tervezett páros mérkőzés során a két játékos megszerezhető pontjainak várható értéke közötti különbség?  (16 pont)   Megoldás. $a)$ Az összes $n$ jegyű számok száma: $9\cdot {10}^{n-1}$. Azoké, melyekben nincs kettes: $8\cdot 9^{n-1}$. A felírható egyenlőtlenség ez alapján: $\begin{array}{c}{\displaystyle \frac{8\cdot 9^{n-1}}{9\cdot {10}^{n-1}}<\frac{1}{3}\mathrm{,}}\end{array}$ átrendezve kapjuk: $0\mathrm{,}{9}^{n-1}<\frac{3}{8}$. Mindkét oldal tízes alapú logaritmusát véve és megoldva az egyenlőtlenséget kapjuk, hogy $\begin{array}{c}{\displaystyle n>\frac{\text{lg}\frac{3}{8}}{\text{lg}0\mathrm{,}9}+1=10\mathrm{,}309\text{...}\mathrm{.}}\end{array}$ Tehát a 11, vagy annál többjegyű számokat vizsgáltuk meg. $b)$ A valószínűség értelmezéséből $0\le p$ és $\frac{3}{5}p+{\left(p+\frac{1}{5}\right)}^2\le 1$ egyszerre kell, hogy teljesüljön. A második egyenlőtlenséget rendezve: $p^2+p-\frac{24}{25}\le 0$ adódik. Ennek a megoldásai a $-\frac{8}{5}\le p\le \frac{3}{5}$ intervallum elemei. Figyelembe véve a $0\le p$ feltételt, $0\le p\le \frac{3}{5}$ a feladat megoldása. $c)$ A döntetlenek nem befolyásolják a megszerzett pontok közötti különbséget, így a győzelmekből számítható várható értékek közötti különbséget kell vizsgálnunk, azaz a következő értéket: $\begin{array}{c}{\displaystyle 100{\left(p+\frac{1}{5}\right)}^2-100\cdot \frac{3}{5}p=100\left(p^2-\frac{1}{5}p+\frac{1}{25}\right)=100\left[{\left(p-\frac{1}{10}\right)}^2+\frac{3}{100}\right]\mathrm{.}}\end{array}$ Ennek a minimum értéke $3$, amit $p=\frac{1}{10}$-nél vesz fel. Maximumát pedig $p=\frac{3}{5}$-nél veszi fel, ahol az értéke 28. Így a megszerzett pontok közötti legnagyobb különbség 28 pont, a legkisebb pedig 3 pont.   6. $a)$ Az $ABC$ szabályos háromszög oldalhossza 2 cm. Az $AC$ és a $BC$ oldal felezőpontjaira illeszkedő egyenes a háromszög köré írt körét a $D$, illetve az $E$ pontokban metszi. Legyen a $D$ a $BC$ oldal $F_a$ felezőpontjához közelebbi metszéspont. Határozzuk meg az $F_{a}D$ távolságot. $b)$ Egy szabályos háromszög magassága 10 cm hosszú. Az egyik oldallal párhuzamos egyenes a háromszöget két olyan részre vágja, melyeknek a kerülete egyenlő. $i)$ Mekkora az egyenes távolsága a vele párhuzamos oldaltól? $ii)$ A háromszöget a magassága mentén megforgatjuk. Mekkora a keletkezett két test térfogata?  (16 pont)   Megoldás. $a)$ I. megoldás. A kérdéses távolságot jelölje $x$ (1. ábr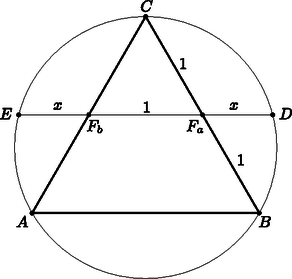a).   1. ábra   $F_a{F}_b=1$, mert középvonal az $ABC$ háromszögben. A szelőszakaszok tétele miatt $\begin{array}{c}{\displaystyle E{F}_a\cdot F_{a}D=C{F}_a\cdot F_{a}B\mathrm{,}}\end{array}$ azaz $\left(1+x\right)x=1$, amiből rendezve az $x^2+x-1=0$ másodfokú egyenletet kapjuk. Az egyenlet megoldása: $x=\frac{-1\pm \sqrt[]{5}}{2}$, amiből csak a nemnegatív $\frac{-1+\sqrt[]{5}}{2}$ érték megoldása a feladatnak. II. megoldás. Használjuk a 2. ábra jelöléseit! 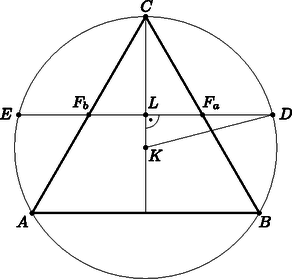  2. ábra   Az $ABC$ háromszög magassága $\sqrt[]{3}$. $K$ harmadolja a magasságot, ezért $CK=\frac{2\sqrt[]{3}}{3}$. (Ez egyben a köré írt kör $r$ sugara is.) Az $F_a{F}_{b}C$ háromszög hasonló az $ABC$ háromszöghöz, a hasonlósági arány $\frac{1}{2}$, ezért $CL=\frac{\sqrt[]{3}}{2}$, és $\begin{array}{c}{\displaystyle LK=CK-CL=\frac{2\sqrt[]{3}}{3}-\frac{\sqrt[]{3}}{2}=\frac{\sqrt[]{3}}{6}\mathrm{.}}\end{array}$ Az $LKD$ háromszög derékszögű, ezért $\begin{array}{c}{\displaystyle L{D}^2=r^2-L{K}^2=\frac{12}{9}-\frac{3}{36}=\frac{5}{4}\mathrm{,}\text{és}LD=\frac{\sqrt[]{5}}{2}\mathrm{.}}\end{array}$ Így $x=LD-L{F}_a=\frac{\sqrt[]{5}}{2}-\frac{1}{2}=\frac{\sqrt[]{5}-1}{2}$.   $b)$ Használjuk a 3. ábra jelöléseit! A kerületek egyenlőségét felírva: 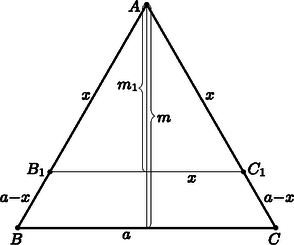$\begin{array}{c}{\displaystyle 3x=x+a+2\left(a-x\right)\mathrm{.}}\end{array}$   3. ábra   Rendezve és $x$-et kifejezve kapjuk, hogy $x=\frac{3}{4}a$. Figyelembe véve az $ABC$ és az $A{B}_1{C}_1$ háromszögek hasonlóságát, a hasonlóság aránya: $\frac{m_1}{m}=\frac{x}{a}=\frac{3}{4}$, amiből $\begin{array}{c}{\displaystyle m_1=\frac{3}{4}m=\frac{3}{4}\cdot 10=7\mathrm{,}5\text{cm. }}\end{array}$ Az egyenes távolsága a párhuzamos oldaltól $10\text{cm - 7,5 cm = 2,5 cm}$. A nagy kúp sugarát az $m=\frac{\sqrt[]{3}}{2}a$ összefüggésből számolva (mindent két tizedesjegyre kerekítve): $r=\frac{a}{2}=\frac{1}{2}\cdot \frac{2}{\sqrt[]{3}}m=\frac{10}{\sqrt[]{3}}=5\mathrm{,}77\text{cm}$. A két kúp hasonlóságát felhasználva, a kis kúp és a nagy kúp térfogatának az aránya: $0\mathrm{,}{75}^3$. A nagy kúp térfogata: $V=\frac{r^2}{3}\pi \cdot m=348\mathrm{,}64{\text{cm}}^3$. 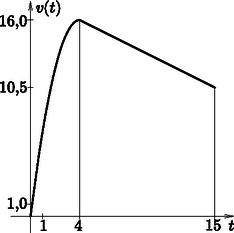A kis kúp térfogata: $V_1=348\mathrm{,}64\cdot 0\mathrm{,}{75}^3=147\mathrm{,}08{\text{cm}}^3$, a maradék rész a csonkakúp térfogata: $\begin{array}{c}{\displaystyle V_{\text{cs}}=348\mathrm{,}64-147\mathrm{,}08=201\mathrm{,}56{\text{cm}}^3\mathrm{.}}\end{array}$   7. A haditengerészet tengeralattjáróinak védelme elsőrendű fontosságú feladat, mert a víz alatt számtalan veszély leselkedik ezekre a mélytengeri hajókra. A védettségüket a mozgékonyságukkal lehet leginkább fokozni, ezért kifejlesztettek egy olyan újfajta meghajtást, amely a tengeralattjáró sebességét a lebegésből (álló helyzetből) a $v\left(t\right)=-t^2+8t$ sebességfüggvény szerint változtatja a $0\le t\le 4$ másodpercekben. Itt a pillanatnyi sebességet a képlet szerint $\frac{\text{m}}{\text{s}}$-ban kapjuk. Ezután a sebesség másodpercenként $0\mathrm{,}5\frac{\text{m}}{\text{s}}$-mal egyenletesen csökken. Egy tengeralattjárót jól védettnek neveznek, ha lebegésből $15$ másodperc alatt a hosszánál nagyobb mértékben képes elmozdulni. Tudjuk, hogy az elmozdulásfüggvény $s\left(t\right)$ deriváltja a $v\left(t\right)$ sebességfüggvény. $a)$ Jól védett kategóriába tartozik-e a 170 m hosszú tengeralattjáró? 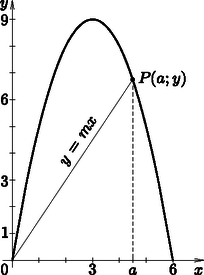$b)$ Tekintsük az $f\left(x\right)=-{\left(x-3\right)}^2+9$ függvény görbéjét a $\left[0;6\right]$ intervallumon. Legyen a görbe egy pontja $P\left(a;y\right)$. Tudjuk, hogy a $P$ pontra illeszkedő $y=mx$ egyenletű egyenes felezi az $f\left(x\right)$ függvény görbéje, az $x=a$ egyenletű egyenes és az $x$ tengely által meghatározott zárt síkidom területét. Adjuk meg $m$ értékét és az egyenes egyenletét.  (16 pont)   Megoldás. Ábrázoljuk közös koordináta-rendszerben a $v\left(t\right)$ függvényt, és a lassulási fázist leíró elsőfokú függvényt.     $a)$ A tengeralattjáró $15$ másodperc alatt megtett útja két részből tevődik össze, ezek összegét képezzük. Az első rész a $v\left(t\right)$ függvény görbéje alatti területtel adható meg. A második, a lassulási fázis egy trapéz területével adható meg. A trapéz magassága 11, alapjai $v\left(4\right)=16$ és a 15. másodpercben a tengeralattjáró pillanatnyi sebessége, ami $16-11\cdot 0\mathrm{,}5=10\mathrm{,}5$. $\begin{array}{c}{\displaystyle \underset{0}{\overset{4}{\int }}\left(-t^2+8t\right)\text{d}t+\frac{16+10\mathrm{,}5}{2}\cdot 11={\left[\frac{-t^3}{3}+4t^2\right]}_0^4+145\frac{3}{4}=\frac{128}{3}+145\frac{3}{4}=188\frac{5}{12}\text{m}\mathrm{,}}\end{array}$ a tengeralattjáró jól védett. $b)$ Ábrázoljuk koordináta-rendszerben az $f$ függvényt.     Az $f$ függvényt átalakítva $f\left(x\right)=-({x-3)}^2+9={-x}^2+6x$. Az $y$ koordinátát kifejezve $a^2+6a$ adódik. A területre vonatkozó feltétel miatt: $\begin{array}{c}{\displaystyle \underset{0}{\overset{a}{\int }}\left(-x^2+6x\right)\text{d}x=a\left(-a^2+6a\right)\mathrm{.}}\end{array}$ Az egyenlet, amit meg kell oldanunk: $\begin{array}{c}{\displaystyle {\left[-\frac{x^3}{3}+3x^2\right]}_0^a=a\left(-a^2+6a\right)\mathrm{.}}\end{array}$ A két oldal szorzat alakja: $\begin{array}{c}{\displaystyle a^2\left(-\frac{a}{3}+3\right)=a^2\left(-a+6\right)\mathrm{,}}\end{array}$ ennek $a=0$ nem a feladat szövegének megfelelő megoldása. Az egyenletet rendezve: $\frac{2}{3}a=3$, ennek a megoldása $a=\frac{9}{2}$, így az $y$ értéke: $\begin{array}{c}{\displaystyle -{\left(\frac{9}{2}\right)}^2+6\cdot \frac{9}{2}=\frac{27}{4}\mathrm{,}}\end{array}$ amiből a meredekség: $\frac{27}{4}:\frac{9}{2}=\frac{3}{2}$, tehát az egyenes egyenlete: $y=\frac{3}{2}x$.   8. $a)$ A $4n^4+1$ kifejezés milyen $n$ természetes szám esetén lesz pozitív prímszám? $b)$ Oldjuk meg a természetes számok halmazán az alábbi egyenletet: $\begin{array}{c}{\displaystyle 2a^2{b}^3+10b^3=15a^2+224.}\end{array}$ (16 pont)   Megoldás. $a)$ Alakítsuk a kifejezést szorzattá: $\begin{array}{c}{\displaystyle 4n^4+1=4n^4+4n^2+1-4n^2={\left(2n^2+1\right)}^2-{\left(2n\right)}^2\mathrm{,}}\end{array}$ alkalmazva a megfelelő azonosságot a $\left(2n^2+2n+1\right)\left(2n^2-2n+1\right)$ alakot kapjuk. Mivel ez prím, és $n\ge 0$, ezért mindkét tényező pozitív kell legyen. Tehát az egyik tényező 1, a másik pedig prím, és az első tényező nagyobb a másodiknál. Tehát csak a $2n^2-2n+1=1$ teljesülhet. Így $2n^2-2n=0$, melynek megoldásai a 0 és az 1. $n=0$ esetén a másik tényező is 1, $n=1$ esetén a másik tényező 5, ami jó megoldás. Összefoglalva egyedül $n=1$ a megoldás, amire a kifejezés értéke: 5 $b)$ Alkalmazzunk megfelelő helyettesítéseket. Legyen $x=a^2$ és $y=b^3$, ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2xy+10y}& {\displaystyle =15x+\mathrm{224,}}\hfill \\ \hfill {\displaystyle 2y\left(x+5\right)}& {\displaystyle =15x+\mathrm{224,}}\hfill \\ \hfill {\displaystyle 2y\left(x+5\right)-15x}& {\displaystyle =\mathrm{224,}}\hfill \\ \hfill {\displaystyle 2y\left(x+5\right)-15\left(x+5\right)+75}& {\displaystyle =\mathrm{224,}}\hfill \\ \hfill {\displaystyle \left(x+5\right)\left(2y-15\right)}& {\displaystyle =149.}\hfill \end{array}}$ Mivel $x+5>0$, ezért $2y-15>0$ is fennáll. 149 prím, ezért a lehetséges felbontások $\begin{array}{c}{\displaystyle \{{\displaystyle \begin{array}{cc}\hfill {\displaystyle x+5}& {\displaystyle =\mathrm{1,}}\hfill \\ \hfill {\displaystyle 2y-15}& {\displaystyle =\mathrm{149,}}\hfill \end{array}}\text{valamint}\{{\displaystyle \begin{array}{cc}\hfill {\displaystyle x+5}& {\displaystyle =\mathrm{149,}}\hfill \\ \hfill {\displaystyle 2y-15}& {\displaystyle =1.}\hfill \end{array}}}\end{array}$ Az első lehetőségből $x=-4$ és $y=82$ adódna, ami lehetetlen, a második egyenletrendszer megoldásai $x=144$ és $y=8$. A megoldások tehát $a=12$ és $b=2$.   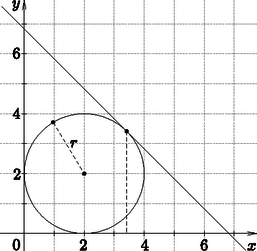9. Adott a koordináta-rendszerben az $x^2+y^2-4x-4y+4=0$ egyenletű kör. $a)$ A zárt körlap a koordináta-rendszer hány darab rácspontját fogja lefedni? $b)$ Húzzunk a körhöz érintőket az első síknegyedben. Ezen érintők közül melyik az, amely a koordináta-tengelyekkel a legkisebb területű háromszöget határozza meg? Írjuk fel az érintő egyenes egyenletét.  (16 pont)   Megoldás. $a)$ A kör egyenlete teljes négyzetté alakítva: ${\left(x-2\right)}^2+{\left(y-2\right)}^2=4$. Ez tehát egy olyan kör, amely a tengelyeket érinti. Készítsünk ábrát.     A kör kerületén $4$ db rácspont van. Belsejében pedig a 3 ‐ 3 rácsegyenes metszéspontjai a megfelelők. Így $4+3\cdot 3=13$ ilyen pont adódik. $b)$ Feladatunk elemi geometriai megfogalmazásban tehát az, hogy adott beírható kör sugár esetén, melyik derékszögű háromszög lesz minimális területű. Megmutatjuk, hogy ez éppen az egyenlőszárú derékszögű háromszög. Ismeretes, hogy a háromszög területe $t=\frac{1}{2}r\left(a+b+c\right)$. Felhasználva Pitagorasz tételét, $t=\frac{1}{2}r\left(a+b+\sqrt[]{a^2+b^2}\right)$. Használjuk most fel a számtani és mértani, valamint a négyzetes és mértani közép közti összefüggéseket: $\begin{array}{c}{\displaystyle \frac{a+b}{2}\ge \sqrt[]{ab}\mathrm{,}\sqrt[]{\frac{a^2+b^2}{2}}\ge \sqrt[]{ab}\mathrm{.}}\end{array}$ Így $a+b\ge 2\sqrt[]{ab}$, $\sqrt[]{a^2+b^2}\ge \sqrt[]{2}\sqrt[]{ab}$ adódik, amit behelyettesítve a terület $\begin{array}{c}{\displaystyle t\ge \frac{1}{2}r\sqrt[]{ab}\left(2+\sqrt[]{2}\right)\mathrm{.}}\end{array}$ A minimális terület $a=b$ esetén valósul meg, vagyis akkor, amikor a háromszög egyenlő szárú. Mivel a háromszög derékszögű, $t=\frac{ab}{2}$. Négyzetre emelés és egyszerűsítések után adódik, hogy $t=\frac{1}{2}{r}^2{\left(2+\sqrt[]{2}\right)}^2$. A mi esetünkben a kör sugara 2 egység, tehát a minimális terület $t_{\underset{}{\overset{}{\text{min}}}}=2{\left(2+\sqrt[]{2}\right)}^2$. Mivel a háromszög egyenlő szárú, az oldal hosszára $a=2\left(2+\sqrt[]{2}\right)$ adódik. Így a keresett egyenes egyenlete $y=mx+b$ alakot használva $y=-x+4+2\sqrt[]{2}$.