Kezdőlap


Cím:	Az 57. Nemzetközi Matematikai Diákolimpia feladatainak megoldása
Füzet:	2016/november, 450 - 455. oldal	PDF \| MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Második nap¹

4. Pozitív egészek egy halmazát illatosnak nevezzük, ha legalább

2

eleme van, és minden eleméhez található legalább egy olyan másik eleme, hogy a két elemnek van közös prímosztója. Legyen

P (n) = n^{2} + n + 1

. Mi a legkisebb olyan pozitív egész

b

érték, amihez található egy nemnegatív

a

egész szám úgy, hogy a

\begin{matrix} {P (a + 1), P (a + 2), ..., P (a + b)} \end{matrix}

halmaz illatos?

Baran Zsuzsanna megoldása. Be fogjuk látni, hogy a legkisebb ilyen

b

pozitív egész a

b = 6

.
A feladat az, hogy minél kevesebb szomszédos pozitív egész számot kell találnunk úgy, hogy azok közül mindegyik

P

-jének legyen közös prímosztója valamelyik másik elem

P

-jével. Ehhez megvizsgáljuk, hogy közeli számok

P

-jeinek milyen közös prímosztója lehet, azaz hogy adott kicsi pozitív egész

x

-ekre milyen

p

prímre lehet

p ∣ P (n)

és

p ∣ P (n + x)

(

n

pozitív egész). Az

x = 1

, 2, 3 és 4-et fogjuk megvizsgálni.
Először is, mivel

n^{2} + n = n (n + 1)

páros, ezért

P (n)

mindig páratlan, így

p

nem lehet 2.

x = 1

-re:

\begin{matrix} (n^{2} + n + 1; {(n + 1)}^{2} + (n + 1) + 1) & = (n^{2} + n + 1; 2 n + 2) = \\ = (n^{2} + n + 1; n + 1) = (n^{2}; n + 1) = 1. \end{matrix}

Azaz

P (n)

-nek és

P (n + 1)

-nek nem lehet közös prímosztója.

x = 2

-re:

\begin{matrix} 0 & \equiv n^{2} + n + 1 \equiv {(n + 2)}^{2} + (n + 2) + 1 = n^{2} + 5 n + 7 (mod p), \\ 0 & \equiv 4 n + 6 (mod p), \\ 2 n & \equiv - 3 (mod p), \\ 0 & \equiv 4 n^{2} + 4 n + 4 \equiv {(- 3)}^{2} + 2 (- 3) + 4 = 7 (mod p) . \end{matrix}

Így csak akkor lehetséges

p ∣ P (n)

és

p ∣ P (n + 2)

, ha

p = 7

és

2 n \equiv - 3 \equiv 4 (mod 7)

, így

n \equiv 2 (mod 7)

. Ilyenkor tényleg fennáll az oszthatóság:

2^{2} + 2 + 1 \equiv 4^{2} + 4 + 1 \equiv 0 (mod 7)

x = 3

-ra:

\begin{matrix} 0 & \equiv n^{2} + n + 1 \equiv {(n + 3)}^{2} + (n + 3) + 1 = n^{2} + 7 n + 13 (mod p), \\ 0 & \equiv 6 n + 12 (mod p), \\ 3 n & \equiv - 6 (mod p), \\ 0 & \equiv 9 n^{2} + 9 n + 9 \equiv {(- 6)}^{2} + 3 \cdot (- 6) + 9 = 27 (mod p) . \end{matrix}

Így csak a

p = 3

jöhet szóba.
Ekkor

1^{2} + 1 + 1 \equiv 0 (mod 3)

, de

0^{3} + 0 + 1 \equiv 2^{2} + 2 + 1 ≢ 0 (mod 3)

, így az

n \equiv 1 (mod 3)

jó, de más nem. Tehát

P (n)

és

P (n + 3)

közös prímosztója csak a 3 lehet, mégpedig ha

n \equiv 1 (mod 3)

x = 4

-re:

\begin{matrix} 0 & \equiv n^{2} + n + 1 \equiv {(n + 4)}^{2} + (n + 4) + 1 = n^{2} + 9 n + 21 (mod p), \\ 0 & \equiv 8 n + 20 (mod p), \\ 2 n & \equiv - 5 (mod p), \\ 0 & \equiv 4 n^{2} + 4 n + 4 \equiv {(- 5)}^{2} + 2 \cdot (- 5) + 4 = 19 (mod p) . \end{matrix}

Így csak a

p = 19

2 n \equiv - 5 \equiv 14 (mod 19)

, azaz

n \equiv 7 (mod 19)

jöhet szóba. Ez megfelelő is:

7^{2} + 7 + 1 \equiv 9^{2} + 9 + 1 \equiv 0 (mod 19)

. Tehát

P (n)

és

P (n + 4)

közös prímosztója csak a 19 lehet, mégpedig ha

n \equiv 7 (mod 19)

.
Most az eddigiek alapján próbáljunk létrehozni egy megfelelő 6 elemű halmazt. Szeretnénk egy olyan

a

-t találni, hogy

P (a + 1)

-nek és

P (a + 5)

-nek,

P (a + 2)

-nek és

P (a + 4)

-nek, illetve

P (a + 3)

-nak és

P (a + 6)

-nak legyen közös prímosztója.
Legyen

b = 6

és

a \equiv 1 (mod 3)

a \equiv 6 (mod 19)

és

a \equiv 0 (mod 7)

(ennek a kínai maradéktétel szerint van pozitív egész megoldása).
Ekkor

a + 1 \equiv 7 (mod 19)

, így

19 ∣ P (a + 1), P (a + 1 + 4)

, míg

a + 2 \equiv 2 (mod 7)

, így

7 ∣ P (a + 2), P (a + 2 + 2)

, végül

a + 3 \equiv a + 6 \equiv 1 (mod 3)

, így

3 ∣ P (a + 3), P (a + 6)

.
Így a fenti

a

mellett a

{P (a + 1), P (a + 2), ..., P (a + 6)}

halmaz mindegyik eleméhez található egy másik elem, amivel van közös prímosztója, azaz a halmaz illatos.
Tegyük fel, hogy van kisebb megfelelő

b

is, azaz létezik

b \leq 5

pozitív egész, amihez létezik

a

pozitív egész, hogy

{P (a + 1), ..., P (a + b)}

illatos.
Nem lehet

b = 2

vagy

b = 3

, mert

P (a + 2)

relatív prím

P (a + 1)

-hez és

P (a + 3)

-hoz is.
Nem lehet

b = 4

, mert akkor

P (a + 2)

relatív prím

P (a + 1)

-hez és

P (a + 3)

-hoz, így

P (a + 4)

-gyel kell közös prímosztója legyen, ami csak a 7 lehet (

P (n)

és

P (n + 2)

közös prímosztója csak a 7 lehet). Hasonlóan

P (a + 3)

-nak

P (a + 1)

-gyel kell közös prímosztója legyen, de ez is csak a 7 lehet. Ez viszont azt jelentené, hogy

P (a + 1)

és

P (a + 2)

egyaránt oszthatóak 7-tel, ami ellentmondás.
Nem lehet

b = 5

sem, mert akkor

P (a + 3)

relatív prím a szomszédjaihoz, így

P (a + 1)

-gyel vagy

P (a + 5)

-tel kell közös prímosztója legyen, ez a prímosztó pedig csak a 7 lehet. Ha

7 ∣ P (a + 3)

, akkor

7 ∤ P (a + 2), P (a + 4)

. Eközben

P (a + 2)

relatív prím a szomszédjaihoz és mivel nem osztható 7-tel, ezért relatív prím

P (a + 4)

-hez is. Ekkor

P (a + 5)

-tel kell közös prímosztója legyen, ami viszont csak a 3 lehet (

P (n)

és

P (n + 3)

közös prímosztója csak a 3 lehet). Hasonlóan

P (a + 4)

-nek

P (a + 1)

-gyel kell közös prímosztója legyen, ami viszont szintén csak a 7 lehet. Ekkor azonban

7 ∣ P (a + 1)

és

7 ∣ P (a + 2)

, ami ellentmondás.
Tehát mégsem lehet

b \leq 5

, a legkisebb megfelelő

b

szám a

b = 6

5. Felírjuk a táblára az

\begin{matrix} (x - 1) (x - 2) \dots (x - 2016) = (x - 1) (x - 2) \dots (x - 2016) \end{matrix}

egyenletet, ahol mindkét oldalon

2016

lineáris faktor szerepel. Mi az a legkisebb pozitív

k

érték, amelyre teljesül az, hogy elhagyhatunk e közül a

4032

lineáris faktor közül pontosan

k

darabot úgy, hogy mindkét oldalon maradjon legalább egy lineáris faktor, és az adódó egyenletnek ne legyen valós gyöke?

Nagy Kartal megoldása. Első lépésként belátjuk, hogy

k > 2015

. Ha kevesebb, mint 2016 lineáris faktort törölnénk ki, akkor lesz egy lineáris faktor ami mindként oldalon fog szerepelni. Legyen ez az

(x - i)

lineáris faktor. Ekkor

i

gyöke lesz az egyenletnek, hiszen ekkor mindkét oldal 0 lenne.
Most pedig megmutatjuk, hogy

k = 2016

-ra van megoldás. Legyen ez az egyenlet:

\begin{matrix} (x - 1) (x - 4) (x - 5) (x - 8) (x - 9) \dots (x - 2013) (x - 2016) = \\ = (x - 2) (x - 3) (x - 6) (x - 7) \dots (x - 2011) (x - 2014) (x - 2015) . \end{matrix}

Most nézzük a két oldalt mint két függvényt. Legyen a bal oldal

g (x)

, a jobb oldal

f (x)

. Azt fogjuk belátni, hogy minden

x

-re

f (x) > g (x)

. Ezt esetenként vizsgáljuk.
1. Ha

x < 1

, akkor mindkét oldal pozitív lesz, így elég azt nézni, hogy

f (x)

abszolút értéke nagy lesz

g (x)

-nek. Bontsuk részekre a függvényeket és hasonlítsuk azok alapján össze:

\begin{matrix} | (x - (4 m + 1)) (x - (4 m + 4)) | < | (x - (4 m + 2)) (x - (4 m + 3)) | . \end{matrix}

Ezt átírhatjuk erre az alakra:

Y (3 + Y) < (1 + Y) (2 + Y)

. A kibontás után látszik, hogy a jobb oldal valóban nagyobb, vagyis

g (x)

tagjai párosíthatók

f (x)

tagjaival úgy, hogy mindig az

f (x)

-es tag legyen a nagyobb. Vagyis ezen az intervallumon

f (x) > g (x)

.
2. Ha

x > 2016

, akkor hasonló módon végigvihető, hogy

f (x) > g (x)

.
3. Ha

1 \leq x \leq 2016

a)

x

egész és

4 m

vagy

4 m + 1

alakú, akkor

g (x) = 0

f (x) > 0

b)

x

egész és

4 m + 2

vagy

4 m + 3

alakú, akkor

g (x) < 0

f (x) = 0

c)

2 m > x > 2 m - 1

, akkor

g (x)

negatív,

f (x)

pozitív.

d)

4 m < x < 4 m + 1

, akkor mindkét függvény pozitív. Vagyis az kell, hogy

| f (x) | > | g (x) |

. Itt is bontsuk részekre a függvényeket:

\begin{matrix} f_{1} (x) & = (x - 2) (x - 3), & f_{2} (x) & = (x - 6) (x - 7), & ..., \\ g_{1} (x) & = (x - 1) (x - 4), & g_{2} (x) & = (x - 5) (x - 8), & ... . \end{matrix}

Itt is könnyen belátható, hogy

f_{i} (x) > g_{i} (x)

. Vagyis itt is igaz, hogy

f (x) > g (x)

e)

4 m + 2 < x < 4 m + 3

, akkor mindkét függvény negatív, ezért azt kell belátni, hogy

| f (x) | < | g (x) |

. A részekre bontás itt így fog kinézni:

\begin{matrix} f_{1} (x) & = (x - 2), f_{2} (x) = (x - 3) (x - 6), ..., \\ f_{1008} (x) = (x - 2011) (x - 2014), f_{1009} (x) = (x - 2015), \\ g_{1} (x) & = (x - 1), g_{2} (x) = (x - 4) (x - 5), ..., \\ g_{1008} (x) = (x - 2012) (x - 2013), g_{1009} (x) = (x - 2016) . \end{matrix}

Itt könnyen belátható, hogy

f_{i} (x) < g_{i} (x)

. Vagyis igaz, hogy

| g (x) | > | f (x) |

, azaz

f (x) > g (x)

.
Ezzel beláttuk, hogy a jobb oldal mindig nagyobb, mint a bal oldal, azaz nem lesz gyöke az egyenletnek.
A megoldás:

k = 2016

6. Adott a síkon

n \geq 2

szakasz úgy, hogy bármely két szakasz keresztezi egymást, és semelyik három szakasznak sincsen közös pontja. Jeromosnak ki kell választania mindegyik szakasznak az egyik végpontját, és oda egy-egy békát elhelyezni úgy, hogy a béka a szakasz másik végpontja felé nézzen. Ezután Jeromos

(n - 1)

-szer fog tapsolni. Mindegyik tapsolásra minden béka azonnal a szakaszon található következő metszéspontra ugrik. A békák az ugrásirányukat soha nem változtatják meg. Jeromos úgy szeretné elhelyezni a békákat, hogy soha ne legyen két béka azonos időben azonos metszésponton.

(a)

Bizonyítsuk be, hogy Jeromos ezt mindig meg tudja tenni, ha

n

páratlan.

(b)

Bizonyítsuk be, hogy Jeromos ezt soha nem tudja megtenni, ha

n

páros.

Gáspár Attila megoldása. Rajzoljunk egy olyan nagy kört, ami az összes szakaszt tartalmazza a belsejében. Hosszabbítsuk meg az összes szakaszt úgy, hogy a végpontjaik a körre kerüljenek. Két szakasz legfeljebb egy pontban metszheti egymást, ezért nem jön létre új metszéspont, tehát a hosszabbítás semmit nem befolyásol. Nevezzük a szakaszvégpontokat belépési és kilépési pontoknak attól függően, hogy indul-e belőle béka, vagy nem. Nyilvánvaló, hogy

n

db belépési és

n

db kilépési pont van.
Tegyük fel, hogy a körön van két szomszédos belépési pont. Az 1. ábrán látható, a két szakasz metszéspontig tartó részei és a köztük lévő, más pontot nem tartalmazó körív által határolt alakzat legyen

X

. Látható, hogy mindegyik szakasz (az

X

-et határoló szakaszokat kivéve) 0 vagy 2 pontban metszi az

X

határvonalát, mert az

X

konvex. A körívet egyik sem metszi, ezért mindegyik a két szakaszt fogja metszeni. A két

X

-et határoló szakaszon így ugyanannyi metszéspont lesz, ez legyen

y

. Mivel

y \leq n - 2

, ezért

y + 1

ugrás után a két béka összeütközik. Ez ellentmondás, tehát nem lehet két szomszédos belépési pont. Ha a békák

n - 1

helyett

n

-szer ugranak, akkor a kilépési pontokba érkeznek. Ilyenkor nem történhet ütközés, ezért ez nem módosítja a feladatot. Nyilvánvaló, hogy ha a békák nem ütköztek, akkor a kilépési pontokból indulva sem ütköznének, ekkor a lépéssorozat visszafelé játszódna le. Ebből következik, hogy nem lehet két szomszédos kilépési pont. Így a körön lévő pontok felváltva kilépési és belépési pontok.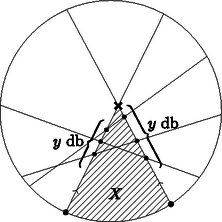

1. ábra

a)

Válasszunk ki egy végpontot, és legyen belépési pont. A többi végpont felváltva legyen kilépési és belépési pont. Egy tetszőleges szakaszt az összes többi metsz, ezért a két oldalán ugyanannyi végpont van. Összesen

2 n

végpont van, ezért egy oldalon

n - 1

db van. Ez páros, ezért a szakasz végpontjai különböző típusúak (2. ábra).

2. ábra

Tegyük fel, hogy van két béka, ami összeütközik. Legyen a 3. ábrán látható, a két szakasz metszéspontig tartó részei és a két belépési pontot összekötő, a két szakasz kilépési pontját nem tartalmazó körív által határolt alakzat

X

. Az

X

konvex, ezért minden szakasz 0 vagy 2 pontban metszi az

X

határvonalát. A két béka ütközik, ezért a két szakasz határvonalán ugyanannyi metszéspont van. A köríven páratlan számú végpont van, mert két belépési pont között vannak. Így összesen páratlan számú pontban metszik a szakaszok az

X

határvonalát. Ez ellentmondás, tehát a békák nem ütköznek.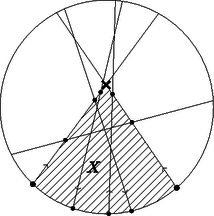

3. ábra

b)

Tegyük fel, hogy lehetséges. Egy szakasz egyik oldalán

n - 1

végpont van. Ez páratlan, ezért a szakasz két végpontja ugyanolyan típusú. Ez ellentmondás (4. ábra).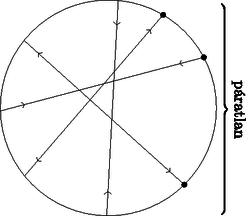

4. ábra

¹Az első nap feladatainak megoldását az októberi számban közöltük.