Cím:	Megoldásvázlatok a 2016/6. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Studium Generale diákszervezet
Füzet:	2016/október, 397 - 403. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Pisti, a focicsapat csapatkapitánya kíváncsi volt, hogy milyen erős a csapat, így készített egy statisztikát. Segítsünk Pistinek a statisztikai értékek kiszámításában. $a)$ A csapattagok átlagosan egyenként egy meccsen 4 km hosszúságú utat futnak. Az út egyik felét 17 km/h-val, míg az út másik felét 14 km/h-val futják. Mennyi a fiúk átlagsebessége?  (6 pont) $b)$ A kezdőcsapat összeállításánál nagyon fontos a megfelelő magasság is. Pisti $183$, Béla $201$, Peti $200$, Marci 191 cm magas. Andris és Bálint magassága azonban elveszett. Szerencsére Pisti már kiszámolta a kezdőcsapat magasságának a következő átlagait (két tizedesjegyre kerekítve): négyzetes átlag: 188,16 cm, számtani átlag: 187,83 cm. Segítsünk kiszámítani Andris és Bálint magasságát, ha tudjuk, hogy Bálint az alacsonyabb kettejük közül. A választ egész számra kerekítve adjuk meg.  (6 pont)   Megoldás. $a)$ Az átlagsebességet az alábbi formulával számíthatjuk ki: $v_{\text{átlag}}=\frac{s_{\text{összes}}}{t_{\text{összes}}}$. A feladat szövegéből tudjuk, hogy az összes út 4 km. Az összes idő pedig $\begin{array}{c}{\displaystyle \frac{2}{17}+\frac{2}{14}=\frac{31}{119}\approx 0\mathrm{,}26\text{ óra.}}\end{array}$ Ezeket behelyettesítve a fenti képletbe: $\begin{array}{c}{\displaystyle v_{\text{átlag}}=\frac{4}{\frac{31}{119}}\approx 15\mathrm{,}35\frac{\text{km}}{\text{h}}\mathrm{.}}\end{array}$ $b)$ A feladat során két helyes képlet alkalmazására van szükség, a számtani átlag képletére: $\begin{array}{c}{\displaystyle \overline{Y}=\frac{\sum _{i=1}^N{Y}_i}{N}\mathrm{,}}\end{array}$ illetve a négyzetes átlag képletére: $\begin{array}{c}{\displaystyle \overline{Y}=\sqrt[]{\frac{\sum _{i=1}^N{Y}_i^2}{N}}\mathrm{.}}\end{array}$ A képletekbe való behelyettesítés után a következő egyenletrendszert kapjuk: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 188\mathrm{,}16}& {\displaystyle =\sqrt[]{\frac{{183}^2+{201}^2+{200}^2+{191}^2+x^2+y^2}{6}}\mathrm{,}}\hfill \\ \hfill {\displaystyle 187\mathrm{,}83}& {\displaystyle =\frac{183+201+200+191+x+y}{6}\mathrm{.}}\hfill \end{array}}$ A feladatot levezetve $y_1\approx 169\mathrm{,}41$ cm, $y_2\approx 182\mathrm{,}57$ cm. Az ezekhez tartozó $x$ számpárok ugyanezek felcserélve, betűszimmetria miatt, így az $x$ értékek kiszámolása nem szükséges. Kerekítés után: Bálint 169 cm, Andris pedig 183 cm magas. Ezekkel az értékekkel számolva a feladat szövegében szereplő átlagokat kapjuk.   2. Néhányan dartsoznak. Adélnak, a ,,Sniper''-nek $\frac{45}{8}$-szor annyi pontja van, mint az $5$. helyen álló Eleknek, illetve $\frac{5}{3}$-szor annyi pontja van, mint a $2$. helyen álló Bélának. A $2$‐$5$. helyen álló emberek pontszámai egy mértani sorozatot alkotnak, továbbá pontszámaik összege $390$. Harmadik helyen Csaba toporzékol, míg a $4$. Dani. A bajnokság során csak egész pontszámuk lehet a versenyzőknek. $a)$ Hány pontja van a játékosoknak külön-külön?  (9 pont) $b)$ Tegyük fel, hogy a játék hátralévő részében még $5$-ször találják el a legértékesebb mezőt, a tripla $20$-at, mely $60$ pontot ér. Mekkora a valószínűsége, hogy a jelenleg $40$ ponttal $6$. helyen álló Feri csak ezekből a dobásokból meg tudja dönteni az eredeti $279$ pontos rekordot, ha feltehetjük, hogy a tripla $20$-ak az első hat helyen lévő emberek között születnek, akik ugyanakkora valószínűséggel dobnak tripla $20$-at, és egy ember akár többet is dobhat?  (4 pont)   Megoldás. $a)$ Első lépésként meghatározzuk a mértani sorozat kvóciensét. Ehhez a $\frac{45}{8}$-ot elosztjuk $\frac{5}{3}$-dal, így $\frac{135}{40}$-et kapunk. Ez  $q^3$-nak felel meg, így a kvóciens $\frac{3}{2}$. A mértani sorozat összegképlete $S_n=a_1\frac{q^n-1}{q-1}$, ahol $a_1$ a legkisebb pontszám, vagyis ,,Purman'' pontszáma. Behelyettesítve $\begin{array}{c}{\displaystyle 390=a_1\frac{1\mathrm{,}{5}^4-1}{1\mathrm{,}5-1}\mathrm{,}\text{amiből}{a}_1=48.}\end{array}$ Ebből ki lehet számolni a többi játékos pontszámát, melyek a következők: Eleké 48, Danié 72, Cecilé 108, Béláé 162 pont. Adélnak pedig (Béla pontját $\frac{5}{3}$-dal beszorozva) 270 pontja van. $b)$ Ferinek minimum 4 tripla 20-at kell dobnia, hogy megdöntse a rekordot (hiszen ha 4-et dob, akkor pont 280 pontja lesz). Ha mindegyiket ő dobja, az csak egyféleképpen történhet meg, ha pedig 1-et más dob, az 25-féleképpen, hiszen megkülönböztetjük, hogy hányadikat dobja más. Az összes eset meghatározásához az ismétléses variáció képletét használjuk: $V_6^{\mathrm{5,}i}=6^5=7776$. Ebből adódóan a valószínűség: $p=\frac{1+25}{7776}\approx 0\mathrm{,}00334$.   3. Dávid úgy dönt, hogy szeretne $13$ SG-s lány között $7$ db ajándékot kisorsolni. Az ajándékok különböző értékűek. Az ajándékok közül $5$ be van csomagolva, $2$ pedig nincs. $a)$ Hányféleképpen oszthatja szét Dávid az ajándékait, ha tudjuk, hogy egy lány többet is kaphat, és már kettő becsomagolt ajándék előre ki lett sorsolva, továbbá Fanni csak a nem becsomagolt ajándékok közül kaphat?  (7 pont) $b)$ Dávid észrevette, hogy a megvásárolt ajándékok egy része selejtes, egy része pedig kopott. A bolt statisztikája szerint a raktárukon lévő $80$ termék közül $13$ darab volt selejtes, $7$ darab kopott és a többi sértetlen. Mennyi a valószínűsége annak, hogy Dávid $2$ darab selejtes és $3$ darab kopott ajándékot hozott el az SG-s lányoknak (a maradék $2$ ajándék sértetlen)?  (6 pont)   Megoldás. $a)$ A feladat során nem kell a már előre kisorsolt ajándékokkal foglalkozni, így 3 becsomagolt és 2 nem becsomagolt maradt. Mivel az ajándékok különböző értékűek és egy lány többet is kaphat, így az ismétléses variáció képletébe kell behelyettesítenünk. Figyelni kell arra is, hogy a becsomagolt ajándékokat csak 12 lánynak oszthatjuk szét. Innen: $V_{12}^{\mathrm{3,}i}\cdot V_{13}^{\mathrm{2,}i}={12}^3\cdot {13}^2=292032$ eset van. $b)$ Az összes eset meghatározása során ismétlés nélküli kombináció képletét kell alkalmazni. Ez alapján: $C_{80}^7=\left(\genfrac{}{}{0ex}{}{80}{7}\right)$. Meg kell határozni azon esetek számát, amikor az adott halmazokból adott mennyiséget vesz ki, ennek módja: $\left(\genfrac{}{}{0ex}{}{13}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{60}{2}\right)$. A valószínűség kiszámításához a kedvező eseteket elosztjuk az összes esettel: $\begin{array}{c}{\displaystyle p=\frac{\left(\genfrac{}{}{0ex}{}{13}{2}\right)\cdot \left(\genfrac{}{}{0ex}{}{7}{3}\right)\cdot \left(\genfrac{}{}{0ex}{}{60}{2}\right)}{\left(\genfrac{}{}{0ex}{}{80}{7}\right)}\approx 1\mathrm{,}521\cdot {10}^{-3}\mathrm{.}}\end{array}$   4. $a)$ Határozzuk meg az $A\cap B$, $A\cup B$, $A\backslash B$ halmazokat, ha az $A$ halmaz a $\text{log}{}_{\left(x^2-1\right)}\left(\frac{-6}{x^2-9}\right)$ függvény értelmezési tartománya, a $B$ halmaz pedig a $\begin{array}{c}{\displaystyle \sqrt[]{-2x^2+2x+60}}\end{array}$ kifejezés értelmezési tartománya.  (9 pont) $b)$ Az SG-s e-learning kurzuson $3$ tantárgyból lehet választani. Matekot összesen $26$, Törit $21$, Közgázt $19$ diák tanul. Tudjuk továbbá, hogy a Közgázt és Törit is tanulók kétszer annyian vannak, mint a Matekot és Közgázt is, illetve azt, hogy a Törit és Közgázt tanulók $4$-gyel többen vannak, mint a Matekot és Törit is tanulók. $15$ diák tanul egynél több tárgyat. Összesen $48$ diák tanul az e-learningen. Hány diák tanul Matekot és Közgázt is?  (4 pont)   Megoldás. $a)$ Első lépésként meg kell határozni az $A$ halmaz elemeit. Mivel logaritmusunk van, az alap 0-nál nagyobb és nem egyenlő 1-gyel: $x^2-1>0$ $\iff$ $x\in \left]-\infty ;-1\right[\cup \left]1;\infty \right[$ és $x^2-1\ne 1$ $\iff$ $x\ne \pm \sqrt[]{2}$. Kikötést kell tenni a logaritmus numeruszára is. Mivel a számláló negatív, csak a nevezőre kell kikötést tenni: $x^2-9<0\iff \left]-3;3\right[$. Az előbb felsorolt három halmaz közös része az $A$ halmaz: $\left(\left]-3;-1\right[\backslash \left\{-\sqrt[]{2}\right\}\right)\cup \left(\left]1;3\right[\backslash \left\{\sqrt[]{2}\right\}\right)$. Meg kell határozni még a $B$ halmazt: $-2x^2+2x+60\ge 0$ $\iff$ $-2\left(x^2-x-30\right)\ge 0$ $\iff$ $-2\left(x-6\right)\left(x+5\right)\ge 0$ $\iff$ $x\in \left[-5;6\right]$. Innen: $\begin{array}{c}{\displaystyle A\cap B=A=\left(\left]-3;-1\right[\backslash \left\{-\sqrt[]{2}\right\}\right)\cup \left(\left]1;3\right[\backslash \left\{\sqrt[]{2}\right\}\right)\mathrm{,}A\cup B=B=\left[-5;6\right]\mathrm{,}A\backslash B=\left\{\varnothing \right\}\mathrm{.}}\end{array}$ $b)$ $|M|=26$, $|T|=21$, $|K|=19$. Vezessük be az alábbi jelöléseket: $|M\cap K|=x$, $|M\cap K\cap T|=y$. Ennek segítségével: $|K\cap T|=2x$, $|M\cap T|=2x-4$. Ez alapján felírhatjuk a következő egyenletrendszert: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 26+21+19-x-2x-\left(2x-4\right)+y}& {\displaystyle =\mathrm{48,}}\hfill \\ \hfill {\displaystyle \left(x-y\right)+\left(2x-y\right)+\left(2x-4-y\right)+y}& {\displaystyle =15.}\hfill \end{array}}$ Az egyenleteket megoldva kapjuk, hogy $y=3$, $x=5$. Tehát 5 diák tanul Matekot és Közgázt is.   II. rész     5. Adott egy kör, melynek középpontja $O\left(8;5\right)$, sugara $4$ egység. Adott továbbá a $h:y=-x+9$ egyenes és a $P\left(0;1\right)$ pont. $a)$ Adjuk meg azon egyenesek metszéspontjait a körrel, amik áthaladnak a $P$ ponton, valamint a $h$ egyenes és a kör egyik metszéspontján.  (10 pont) $b)$ Adjuk meg az új egyenesek körhöz viszonyított helyzetét/helyzeteit.  (2 pont) $c)$ Adjuk meg a $h$ és a $g:y=5$ egyenesek hajlásszögét.  (4 pont)   I. megoldás. $a)$ Felírjuk a kör egyenletét: $k:{\left(x-8\right)}^2+{\left(y-5\right)}^2=16$. Egyenletrendszerben megoldva megkeressük $k$ metszéspontjait a $h$ egyenessel. Ezek a következők lesznek: $Q\left(4;5\right)$, $Z\left(8;1\right)$. Két pont alapján felírjuk a keresett egyenesek egyenletét: 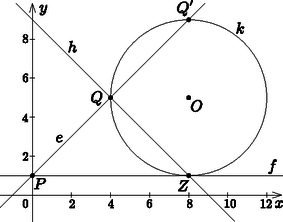$\begin{array}{c}{\displaystyle e:\left(4-0\right)\cdot \left(y-1\right)=\left(5-1\right)\cdot \left(x-0\right)\mathrm{,}}\end{array}$ azaz $y=x+1$, $\begin{array}{c}{\displaystyle f:\left(8-0\right)\cdot \left(y-1\right)=\left(1-1\right)\cdot \left(x-0\right)\mathrm{,}}\end{array}$ azaz $y=1$.     A kör és az egyes egyenesek egyenleteit egyenletrendszerben megoldjuk. Ebből megkapjuk, hogy az $e$ egyenes és a $k$ kör metszéspontjai: $Q\left(4;5\right)$, $Q\text{'}\left(8;9\right)$, továbbá az $f$ egyenes és a $k$ kör érintési pontja: $Z\left(8;1\right)$. $b)$ Az $e$ egyenes szelője, az $f$ egyenes pedig érintője a $k$ körnek. $c)$ A két egyenes irányvektora: $v_g\left(1;0\right)$, illetve $v_h\left(1;-1\right)$. Két vektor skaláris szorzatának átalakított képletével a következőt kapjuk: $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{1\cdot 1+0\cdot \left(-1\right)}{\sqrt[]{0^2+{\left(-1\right)}^2}\cdot \sqrt[]{1^2+1^2}}=\frac{\sqrt[]{2}}{2}\mathrm{,}}\end{array}$ amiből $\alpha ={45}^{\circ }$.   II. megoldás. Vegyük észre, hogy $g$ párhuzamos az $x$ tengellyel. Ezért a két egyenes hajlásszögét megkapjuk, ha felírjuk az $m=\text{tg}\alpha$ összefüggést. Behelyettesítve: $-1=\text{tg}\alpha$, amiből $\alpha ={135}^{\circ }$. Mivel két egyenes hajlásszögén mindig az általuk meghatározott 2 szög közül a kisebbet értjük, így a hajlásszög értéke ${180}^{\circ }-{135}^{\circ }={45}^{\circ }$.   6. $a)$ Összeszorozzuk az első $100$ pozitív egész számot. Hány $0$ áll az így képzett szám végén?  (10 pont) $b)$ Határozzuk meg azt a négyjegyű számot, amely eleget tesz a következő állításnak: $\overline{abcd}+\overline{abc}-\overline{ab}+\overline{a}=2925$.  (6 pont)   Megoldás. $a)$ Egy szám végén annyi nulla áll, ahányadik hatványával a 10-nek osztható a szám. A tíz prímtényezős felbontása: $2\cdot 5=10$. Ebből az következik, hogy ahány számpárost tudunk összeállítani 2-esekből és 5-ösökből, annyi 0 lesz a számunk végén. 1‐100-ig a 2-vel és annak hatványaival osztható számokból több van, mint az 5-tel és annak hatványaiból oszthatóakból, ezért minden 5-öshöz fogunk találni 2-es szorzópárt, így elég az 5-ösök darabszámát megállapítani. Nézzük meg, hogy hány számban szerepel az 5 első hatványa. $100:5=20$, tehát 20 db 5-öst kapunk. Az 5 második hatványa: $100:25=4$. Minden szám 2-vel növelné az 5-ösök mennyiségét, de ezeket egyszer már számoltuk, így csak 4-gyel növekszik a darabszám. Mivel $5^3>100$, ezért több lehetőség nincs. Ez összesen tehát $20+4=24$ db 5-ös. Tehát a szám végén pontosan 24 nulla áll. $b)$ Át kell alakítani az egyenletet: $1091a+109b+11c+d=2925$. Kikötést kell tenni: $1\le a\le 9$, $0\le b$, $c\mathrm{,}d\le 9$, $a\mathrm{,}b\mathrm{,}c\mathrm{,}d\in \text{Z}$. $a=2$, hiszen máshogy az egyenlet nem teljesülhet. $\begin{array}{c}{\displaystyle 2182+109b+11c+d=2925\iff 109b+11c+d=743.}\end{array}$ $b=6$, hiszen máshogy az egyenlet nem teljesülhet. $\begin{array}{c}{\displaystyle 654+11c+d=743\iff 11c+d=89.}\end{array}$ $c=8$, hiszen máshogy az egyenlet nem teljesülhet. $\begin{array}{c}{\displaystyle 11c+d=89\iff 88+d=89.}\end{array}$ Tehát $d=1$. Innen a szám: $\overline{abcd}=2681$.   7. $a)$ Egy trapézt, melynek alapjai $2$ és 8 cm, szárai pedig $3$ és 4 cm hosszúak, a rövidebbik alapjánál fogva megforgatunk. $b)$ Mekkora az így keletkezett forgástest felszíne és térfogata?  (10 pont) $c)$ Mekkora a térfogata annak a legkisebb gömbnek, amibe beleférne ez a test?  (6 pont) 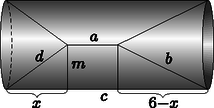  Megoldás. $a)$ Észre kell venni, hogy a feladat esetében egy hengerről és két kúpról van szó. Ki kell számolni a trapéz magasságát, amit egy kétismeretlenes egyenlet segítségével tudunk megtenni, ha kivágjuk a trapéz téglalap részét középről. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle m^2+x^2}& {\displaystyle =3^2\mathrm{,}}\hfill \\ \hfill {\displaystyle m^2+{\left(6-x\right)}^2}& {\displaystyle =4^2}\hfill \end{array}}\}\Rightarrow x=\frac{29}{12}\mathrm{,}m=\frac{\sqrt[]{455}}{12}\mathrm{.}}\end{array}$ Ezután a henger és a kúp térfogatának kiszámítása következik. Legyen $c$ a trapéz hosszabbik alapja, $c=2$ cm, $m$ a trapéz magassága és $x$ az egyik szár hosszabbik alapra eső vetülete. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V_{\text{test}}}& {\displaystyle =V_{\text{henger}}-V_{\text{1.kúp}}-V_{\text{2.kúp}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =m^2\pi \cdot c-\frac{m^{2}x\pi }{3}-\frac{m^2\left(6-x\right)\pi }{3}\approx \frac{455}{18}\pi -2\mathrm{,}55\pi -3\mathrm{,}77\pi \approx 18\mathrm{,}96\pi \approx 59\mathrm{,}56{\text{ cm}}^3\mathrm{.}}\hfill \end{array}}$ Felszínszámításnál a henger, illetve a kúpok palástjára lesz szükség: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle A_{\text{test}}}& {\displaystyle =A_{\text{palást(henger)}}+A_{\text{palást(1.kúp)}}+A_{\text{palást(2.kúp)}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2m\pi \cdot c+4m\pi +3m\pi \approx 28\mathrm{,}44\pi +7\mathrm{,}11\pi +5\mathrm{,}33\pi =40\mathrm{,}88\pi \approx 128\mathrm{,}44{\text{ cm}}^2\mathrm{.}}\hfill \end{array}}$     $b)$ Ahhoz, hogy meghatározzuk a köré írható gömb sugarát, a síkmetszetet kell megvizsgálni. Egy olyan téglalap átlóját nézzük, melynek egyik oldala 8 cm, a másik pedig $2m$, azaz $\frac{\sqrt[]{455}}{6}$. Innen az átló hossza Pitagorasz-tétellel kiszámítva (két tizedesjegyre kerekítve): 8,75 cm. Ebből a sugár: $r\approx 4\mathrm{,}38$ cm. A gömb térfogatát pedig a következő képlettel határozzuk meg: $\begin{array}{c}{\displaystyle V_{\text{gömb}}=\frac{4\cdot r^3\pi }{3}\approx 351\mathrm{,}98{\text{ cm}}^3\mathrm{.}}\end{array}$   8. $a)$ Oldjuk meg az alábbi egyenletrendszert: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 9^x\cdot {343}^y}& {\displaystyle ={49}^x\cdot {27}^y\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{cos}\left(2x+\frac{9}{2}y\right)+\text{cos}\left(\frac{11}{3}x+2y\right)}& {\displaystyle =-\sqrt[]{3}\mathrm{.}}\hfill \end{array}}}\end{array}$ (16 pont)   Megoldás. A két egyenletet megfigyelve rá lehet jönni, hogy érdemes az elsővel kezdeni. Ezt átalakítva a következőt kapjuk: $\begin{array}{c}{\displaystyle \frac{7^{3y}}{3^{3y}}=\frac{7^{2x}}{3^{2x}}\iff {\left(\frac{7}{3}\right)}^{3y}={\left(\frac{7}{3}\right)}^{2x}\mathrm{.}}\end{array}$ Az exponenciális függvény szigorú monotonitása miatt: $3y=2x$ $\iff$ $y=\frac{2x}{3}$. Ezt már be tudjuk helyettesíteni a második egyenletbe. Az egyenletet átalakítva kapjuk, hogy $\text{cos}\left(5x\right)=-\frac{\sqrt[]{3}}{2}$. Az egyenletet megoldva megkapjuk a következő értékeket: $x_1=\frac{1}{6}\pi +\frac{2k\pi }{5}$, $x_2=-\frac{1}{6}\pi +\frac{2l\pi }{5}$, $k\mathrm{,}l\in \text{Z}$. Visszahelyettesítve: $y_1=\frac{1}{9}\pi +\frac{4k\pi }{15}$, $y_2=-\frac{1}{9}\pi +\frac{4l\pi }{15}$, $k\mathrm{,}l\in \text{Z}$.   9. $a)$ Egy derékszögű háromszög oldalai egy számtani sorozat egymást követő elemei. A háromszög kerülete 36 cm. Milyen hosszúak a háromszög oldalai?  (5 pont) $b)$ Hány megoldása van az $|x^2-4x-5|=p$ egyenletnek a $p$ paraméter függvényében?  (11 pont)   Megoldás. $a)$ A feladat megoldásához egy kétismeretlenes egyenletrendszert kell felírnunk. Az első a kerület meghatározásából következik, a második pedig a Pitagorasz-tétel felírása. ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(a_2-d\right)+a_2+\left(a_2+d\right)}& {\displaystyle =\mathrm{36,}}\hfill \\ \hfill {\displaystyle {\left(a_2-d\right)}^2+a_2^2}& {\displaystyle ={\left(a_2+d\right)}^2\mathrm{.}}\hfill \end{array}}$ Az első egyenletet rendezve: $a_2=12$. Ezt behelyettesítve a második egyenletbe: $d=3$. A háromszög oldalai 9, 12, 15 cm hosszúak. $b)$ Először számoljuk ki a másodfokú kifejezés zérushelyeit: $x_1=-1$; $x_2=5$. Így a kifejezés lokális szélsőértéke az $x=\frac{x_1+x_2}{2}=2$ helyen van. Értéke: $y=-9$. Így már fel tudjuk rajzolni a függvény grafikonját (az abszolút érték miatt azokat a pontokat, amelyek második koordinátája negatív, tükrözzük az $x$ tengelyre): A $p$ értékétől függően annyi megoldása lesz az egyenletnek, ahány metszéspont keletkezik a függvény grafikonjának és egy, az $x$ tengellyel párhuzamos egyenesnek. Ha $p<0$, akkor nincs megoldás. Ha $p=0$, akkor 2 megoldás van. Ha $0<p<9$, akkor 4 megoldás van. Ha $p=9$, akkor 3 megoldás van. Ha $p>9$, akkor ismét 2 megoldás van.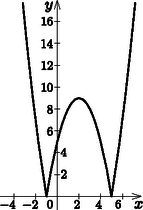