A hagyományoknak megfelelően ebben az évben is közöljük a nyári matematikai diákolimpia feladatainak a megoldásait; lényegében úgy, ahogyan a legilletékesebbek, a magyar csapat tagjai leírták. Közreműködésüket köszönjük és ezúton is gratulálunk eredményeikhez.

 

Williams Kada megoldása. A bonyolult ábra miatt célszerű egy jól megszerkesztett ábrán minden újonnan felvett pontra megvizsgálni, milyen tulajdonságai vannak. Miután az ábra rejtelmeit kiismertük, a befejezés önként fog adódni.
A szögszámításhoz legyen

$\begin{array}{c}{\displaystyle BAC\sphericalangle =CAD\sphericalangle =ACD\sphericalangle =DAE\sphericalangle =ADE\sphericalangle =\alpha \mathrm{,}}\end{array}$

ezek egyenlőségét a $D$ és $E$ pont definíciója indokolja. Ekkor $BFC\sphericalangle =FBA\sphericalangle +FAB\sphericalangle =2\alpha$. A kerületi, illetve kerületi és középponti szögek tételét és azok megfordítását KT, illetve KKT rövidíti.
A következő lépésekben igazoljuk a feladat állítását:
1. Az $ABC$ kör középpontja $D$.
2. $B$, $C$, $D$, $F$ egy $k$ körre illeszkedik.
3. $ABCD\sim AFDE$.
4. $B$, $F$, $E$ egy egyenesen van.
5. $A$, $B$, $M$, $D$, $E$ egy $\ell$ körre illeszkedik.
6. Az $X$ pont is a $k$ körön van.
7. $MXEF$ húrtrapéz, körülírt köre $m$.
8. A hatványpont-tételt $k$, $\ell$, $m$ körökre alkalmazva készen vagyunk.
Az egyes lépések belátása lényegében csak szögszámítás, így érdemes magának az Olvasónak megpróbálni ellenőrizni őket.
A lépések indoklása alább olvasható: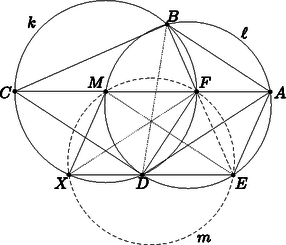

 

 

1. $ABC\sphericalangle ={90}^{\circ }+\alpha$ és $ADC\sphericalangle ={180}^{\circ }-2\alpha$ (mert $DA=DC$). KKT miatt $D$ csakis az $ABC$ kör középpontja lehet.
2. Ez KT-vel adódik: $BFC\sphericalangle =2\alpha =BDC\sphericalangle$, utóbbi az $ABC$ körre vett KKT miatt.
3. A $k$ körbeli KT-ből $CDF\sphericalangle ={90}^{\circ }$, így $AFD\sphericalangle =CDF\sphericalangle +DCF\sphericalangle ={90}^{\circ }+\alpha$. Innen két szög egyezése miatt $ABC\sim AFD$, de $ADC\sim AED$ miatt $ABCD\sim AFDE$ is igaz.
4. Mivel $DA=DB$ (1. lépés), a hasonlóságból $EA=EF$, s így $EFA\sphericalangle =2\alpha =BFC\sphericalangle$, vagyis $BF$ és $FE$ egyenes egybeesik.
5. $CBF\sphericalangle ={90}^{\circ }$ lévén $\overline{CF}$ a $k$ átmérője, $M$ így $k$ középpontja. Innen világos, hogy $MBF\sim DBA\sim EFA$, mert $2\alpha$ alapon fekvő szögű egyenlő szárú háromszögek. A 4. lépés miatt $BMA\sphericalangle =BDA\sphericalangle =BEA\sphericalangle$ adódik, és így KT szerint $A$, $B$, $M$, $D$, $E$ egy körön van.
6. $EDA\sphericalangle =DAC\sphericalangle =\alpha$ lévén $DE\parallel AC$, vagyis $E$, $D$, $X$ kollineáris. $AMXE$ paralelogrammából $MXD\sphericalangle =MAE\sphericalangle =2\alpha$, és az $\ell$ körbeli KT-ből $MDE\sphericalangle ={180}^{\circ }-MAE\sphericalangle$, amiért $MDX\sphericalangle =2\alpha$. Tehát $MD=MX$, azaz $X$ a $k$ körön van.
7. Az $AMXE$ paralelogrammából az $EFA$ egyenlő szárú háromszöget kivágva egy húrtrapézt kapunk, az $MXEF$ húrtrapézt.
8. A $k$ és $\ell$ körök hatványvonala $BD$, a $k$ és $m$ köröké $FX$, az $\ell$ és $m$ köröké pedig $ME$. A hatványpont-tétel szerint e három egyenes egy pontra illeszkedik vagy párhuzamos. Nyilván nem párhuzamosak, ezért egy ponton mennek át.

 

Megjegyzés. Adható két másik, szintén tanulságos megközelítés, ami elsősorban nem köröket vizsgál. Kulcsészrevétel az 1‐3. lépések után, hogy $BCDF$ és $AFD$ körök sugara egyenlő, hisz $FD$ közös húrjukhoz mindkettőben $\alpha$ kerületi szög tartozik. Az adódó egyenlő szakaszokból az alábbi befejezések kínálkoznak:
$\left(a\right)$ $ME$-re tükrözve $B\mathrm{,}D$ képe $X\mathrm{,}F$ lesz, így $BD$ és $FX$ az $ME$ szimmetriatengelyen metsz;
$\left(b\right)$ Az $MXEF$ húrtrapéz átlói oly szögűek, hogy a $BMF$ körön messék egymást, így szimmetria miatt az $MF$ ív felezőpontjára illeszkednek, akárcsak az $MBF$ szög $BD$ szögfelezője.

 

2. Határozzuk meg azokat a pozitív egész $n$ számokat, amelyekre egy $n\times n$-es táblázat minden mezőjére az I, M, O betűk valamelyikét tudjuk írni úgy, hogy:

$•$	minden sorban és minden oszlopban a mezők egyharmadára I, egyharmadára M és egyharmadára O betű van írva; és

$•$	minden átlóban, ha az átlóban lévő mezők száma $3$ többszöröse, akkor ezen mezők egyharmadára I, egyharmadára M és egyharmadára O betű van írva.

Megjegyzés: Egy $n\times n$-es táblázat sorait és oszlopait természetes módon $1$-től $n$-ig számozhatjuk. Így minden mezőhöz egy pozitív egészekből álló $\left(i\mathrm{,}j\right)$ számpár tartozik, ahol $1\le i\mathrm{,}j\le n$. $n>1$ esetén a táblázatnak $4n-2$ átlója van, amelyek kétfélék lehetnek. Egy első típusú átló az összes $\left(i\mathrm{,}j\right)$ mezőkből áll, amelyekre $i+j$ egy adott konstans, egy második típusú átló pedig az összes $\left(i\mathrm{,}j\right)$ mezőkből áll, amelyekre $i-j$ egy adott konstans.

 

Lajkó Kálmán megoldása. Keressük meg az ilyen $n\times n$-es négyzeteket! Ha egy négyzetre van megfelelő kitöltés, akkor $3\mid n$, ez nyilvánvaló.
Azt se nehéz látni, hogy ha van egy $n\times n$-es négyzetre egy kitöltésünk, akkor minden $\left(kn\right)\times \left(kn\right)$-es négyzetre is, hiszen jó kitöltésű $n\times n$-es négyzetből $k^2$-et egymásra lehet pakolni, ekkor a sorok és oszlopok nyilván eleget tesznek a feltételeknek, és az átlók is, mivel belátható, hogy ha egy átló hossza a $kn$-es négyzetben hárommal osztható, akkor az átlónak az egyes $n$-es négyzetekkel vett metszetei is hárommal osztható hosszúságúak.

 

 

Érdemes kis négyzetekre az állítást kipróbálni, az $n=9$ esetre van kitöltés is, így már lehet tudni, hogy a $9\mid n$-es négyzetekre mindig van kitöltés.
Ezután megpróbáljuk belátni, hogy ha $n$ nem osztható kilenccel, de hárommal igen, akkor nem lehet kitölteni a négyzetet.
Ezt indirekten csináljuk, tegyük fel, hogy ki lehet tölteni egy ilyen $\left(n=3k\right)$-s táblázatot, ahol $k$ nem osztható $3$-mal.
Erre a csomó betűre vonatkozó hárommal való oszthatóságot össze lehet adogatni, ki lehet vonni egymásból, az eredményre is igaz lesz hogy a betűk egyharmada I, M és O (ez ilyen egyenletrendszeres ötlet). Ezt úgy kell érteni, hogy ha többször van egy mező I betűje az összegben, akkor annyiszor adódik hozzá az I-k számához, vagy a kivonás miatt lehet hogy negatív sokszor szerepel az összegben, és ekkor ez levonódik az I-k számából. Az összegben tehát mezők betűi szerepelnek, egész sokszor, és az I-k, M-ek és O-k száma azonos.

 

 

Vegyük a táblázatunkat, adjuk össze az összes hárommal osztható átlót (vagyis hogy összesen hány I, M, O van bennük összesen), adjuk hozzá a 2.; 5.; 8.; $\text{...}$; $\left(3l+2\right)$-edik oszlopokat, és ebből vonjuk ki az összes az 1., 3., 4., 6. stb. sorokat, vagyis a nem $\left(3l+2\right)$-edik sorokat. Nézzük meg, hogy ebben hány darab I betű van. Az átlókból van $3;6;\text{...};3k;3k-3;\text{...};3$ hosszú, mindkét irányban, ezekben összesen $2\left(1+2+\text{...}k+1+2+\text{...}+\left(k-1\right)\right)=k\left(k+1\right)+\left(k-1\right)k=2k^2$ darab I betű van. Az oszlopokban van $\frac{kn}{3}=k^2$, és ebből még le kell vonni a sorokban lévő I-k számát, ami $2k\cdot \frac{n}{3}=2k^2$. Ezeket összegezve, az I-k száma: $2k^2+k^2-2k^2=k^2$, ami hárommal nem osztható.
Viszont ha megnézzük, hogy az egyes mezőket hányszor számoltunk az összegben, akkor azt figyelhetjük meg, hogy a nem $3l+2$ alakú sorokban lévő mezők pont kiesnek, és a visszamaradó mezőket mind háromszor számoltuk meg, a két átlóban és az oszlopokban, ezek a $\left(3x+2;3y+2\right)$ koordinátájú mezők. Ez azt jelenti, hogy az I-k száma az összegben hárommal osztható kell hogy legyen. Ez ellentmondás.

 

3. Legyen $P=A_1{A}_2\text{...}{A}_k$ egy konvex sokszög a síkon. Az $A_1\mathrm{,}{A}_2\mathrm{,}\text{...}\mathrm{,}{A}_k$ csúcsok koordinátái egész számok, és ezek a csúcsok egy körön fekszenek. Legyen $S$ a $P$ sokszög területe. Adott egy $n$ páratlan pozitív egész szám, amire teljesül az, hogy a $P$ sokszög minden oldalhosszának a négyzete egy $n$-nel osztható egész szám. Bizonyítsuk be, hogy $2S$ egy $n$-nel osztható egész szám.

 

Szabó Barnabás megoldása.
Lemma. Ha $x$ és $y$ egészek, akkor $x^2\mid y^2$ esetén $x\mid y$.
Bizonyítás. $x\nmid y$ esetén létezik egy $q$ prím és $r$ nemnegatív egész, melyekre $q^r\mid x$ de $q^r\nmid y$, ekkor viszont $q^{2r}\mid x^2$ és $q^{2r}\nmid y^2$, tehát $x^2\mid y^2$ nem teljesülhetne.
A feladat állítását $k$-ra vonatkozó teljes indukcióval fogjuk belátni.
$k=3$ esetén feltehető, hogy az $A_1$, $A_2$ és $A_3$ csúcsok koordinátái rendre $\left(\mathrm{0,0}\right)$, $\left(a_1\mathrm{,}{b}_1\right)$ és $\left(a_2\mathrm{,}{b}_2\right)$ (ahol $a_i$, $b_i$ egészek). Tudjuk, hogy $n\mid a_1^2+b_1^2$ és $n\mid a_2^2+b_2^2$, továbbá $n\mid {\left(a_1-a_2\right)}^2+{\left(b_1-b_2\right)}^2=\left(a_1^2+b_1^2\right)+\left(a_2^2+b_2^2\right)-2\left(a_1{a}_2+b_1{b}_2\right)$, mivel $n$ páratlan, így $n\mid a_1{a}_2+b_1{b}_2$. Innen $n^2\mid \left(a_1^2+b_1^2\right)\left(a_2^2+b_2^2\right)-{\left(a_1{a}_2+b_1{b}_2\right)}^2={\left(a_1{b}_2-a_2{b}_1\right)}^2$. Ebből $n\mid a_1{b}_2-a_2{b}_1$ következik. A jól ismert területképlet alapján

$\begin{array}{c}{\displaystyle 2S=|a_1{b}_2-a_2{b}_1|\mathrm{,}\text{azaz}n\mid 2S\mathrm{,}}\end{array}$

és ezt kellett belátni.
Nyilvánvalóan elegendő az állítást prímhatvány $n$-re belátni (ha $x\mid 2S$ és $y\mid 2S$, ahol $\left(x\mathrm{,}y\right)=1$, akkor $xy\mid 2S$). Legyen $n=p^{\alpha }$, $p>2$. Esetünkben $k\ge 4$ és tegyük fel, hogy az állítást minden $k$-nál kisebb (de legalább 3) pozitív egészre beláttuk. Találni fogunk egy átlót, amely hosszának négyzete osztható $n$-nel, így ezen átló mentén félbevágva $P$-t két kisebb oldalszámú sokszöget kapunk, $P_1$-et (területe $S_1$) és $P_2$-t (területe $S_2$), amelyekre teljesül a feladat feltétele. Az indukciós feltevés miatt $n\mid 2S_1+2S_2=2S$, azaz készen lennénk a feladattal. Tehát már csak egy megfelelő átlót kell találnunk. $P$ rácssokszög, így a Pitagorasz-tétel alapján $P$ minden átlójának négyzete egész szám. Vegyük az átlók közül azt (vagy az egyiket néhány közül), amelyik hosszának négyzetében $p$ kitevője minimális. Legyen ez az $AC$ átló. Az $A$-val szomszédos csúcsok $B$ és $D$. Legyen az $AB$, $BC$, $CD$, $DA$, $AC$ és $BD$ szakaszok hossza rendre $a$, $b$, $c$, $d$, $e$, $f$. Az $ABCD$ húrnégyszögre a Ptolemaiosz-tételt felírva kapjuk, hogy

$\begin{array}{c}{\displaystyle ac+bd=ef\mathrm{,}}\end{array}$

(1)

ezt négyzetre emelve

$\begin{array}{c}{\displaystyle a^2{c}^2+b^2{d}^2+2abcd=e^2{f}^2\mathrm{.}}\end{array}$

(2)

Legyen $\beta$ az a legnagyobb nemnegatív egész, melyre $p^{\beta }\mid e^2$. Ha $\beta \ge \alpha$, akkor $AC$ megfelelő átló. A továbbiakban feltesszük, hogy $\beta <\alpha$. Ekkor $p^{\alpha }\mid a^2$ és $p^{\beta }\mid c^2$ (ha $CD$ átló, akkor ez $AC$ választása miatt igaz, ha $CD$ oldal, akkor $\beta <\alpha$ miatt), tehát $p^{\alpha +\beta }\mid a^2{c}^2$. Hasonlóan $p^{\alpha +\beta }\mid b^2{d}^2$. Mivel $e^2{f}^2$ is egész, így (2) alapján $2abcd$ is az. Viszont $p^{2\left(\alpha +\beta \right)}\mid 4a^2{b}^2{c}^2{d}^2$, így $p^{\alpha +\beta }\mid 2abcd$. Ezt felhasználva (2)-ből következik, hogy $p^{\alpha +\beta }\mid e^2{f}^2$, így $p^{\beta +1}\nmid e^2$ miatt $p^{\alpha }\mid f^2$, azaz ekkor a $BD$ átló megfelelő.