Cím:	Rugalmas testek ütközése
Szerző(k):	Gnädig Péter ,  Szegedi Ervin
Füzet:	2017/május, 298 - 303. oldal	PDF  |  MathML
Témakör(ök):	Szakmai cikkek, Hullámterjedés rugalmas közegben
Hivatkozás(ok):	Feladatok: 2017/május: 4948. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Ütközésekről általában A középiskolai fizikaórák és a fizikafeladványok1 gyakori témája az ütközés. Megtanuljuk, hogy az ‐ általában igen rövid ideig tartó ‐ ütközés alatt a belső erők nagy erőlökése mellett a külső erők hatása elhanyagolható (a rendszer zártnak tekinthető), és emiatt az ütköző testek összes lendülete (másnéven impulzusa) megmaradó mennyiség. Az ütköző testek összes mozgási energiája általában nem marad állandó, hanem ‐ kisebb vagy nagyobb mértékben ‐ lecsökken. A csökkenés mértékétől függően beszélünk rugalmas (másnéven tökéletesen rugalmas), rugalmatlan és tökéletesen rugalmatlan ütközésről. A rugalmatlanság fokát számszerűen az ún. ütközési számmal (ütközési együtthatóval) jellemezhetjük, ami a tömegközépponti koordináta-rendszerben mért relatív sebességcsökkenésből kapható meg. Ha $v_{\mathrm{1,2}}$ a két test sebessége az ütközés előtt, $v{\text{'}}_{\mathrm{1,2}}$ pedig az ütközés után, akkor $\begin{array}{c}{\displaystyle k=\frac{v_1\text{'}}{v_1}=\frac{v_2\text{'}}{v_2}\text{(a tkp.-i rendszerben).}}\end{array}$ Ugyanezt a számot egy tetszőleges (tehát nem feltétlenül a tömegközépponti) koordináta-rendszerben így számolhatjuk: $\begin{array}{c}{\displaystyle k=\frac{|\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}{\text{'}}_1-\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}{\text{'}}_2|}{|{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_1-{\text{<span style="font-weight: bold;"><span style="font-style: italic;">v</span></span>}}_2|}\text{(bármilyen koordináta-rendszerben)}\mathrm{.}}\end{array}$ (Lássuk be, hogy a kétféle definíció ugyanazt a $k$ számot adja!) Rugalmas ütközésekre $k=1$, rugalmatlanokra $0<k<1$, és végül tökéletesen rugalmatlan ütközéseknél $k=0$. Nagymértékben leegyszerűsíti az ütközések tárgyalását, ha az ütköző testek tömegpontoknak tekinthetők. Ehhez nem elegendő az, hogy a méretük kicsi legyen, fontos feltétel az is, hogy ne forogjanak. A tömör gumilabda (trükklabda) vagy egy biliárdgolyó például úgy pattan vissza az ütközés után, hogy még akkor is forgásba jön, ha eredetileg nem forgott. Hiába kicsiny az így ütköző test mérete, a forgási energiája ugyanolyan nagy lehet, mint a tömegközéppontjának mozgásához köthető ,,transzlációs'' (haladási) mozgási energiája. Az ütköző testek általában egy kis felületen érintkeznek. Erre a felületre állított $\text{<span style="font-weight: bold;"><span style="font-style: italic;">n</span></span>}$ egységvektort az ütközés normálisának nevezzük. Centrális az ütközés, ha az ütközési normális átmegy mindkét test tömegközéppontján. (Ilyen ütközés során a testek nem jöhetnek forgásba, ha az ütközés előtt nem forogtak.) Egyenes ütközésről akkor beszélünk, ha a sebességvektorok egymással is és az ütközési normálissal is párhuzamosak. Ebben az esetben a testek tömegközéppontjának sebessége az ütközés után is ugyanolyan (vagy ellentétes) irányú lesz, mint korábban volt. A legegyszerűbb eset ‐ nyilván ‐ a centrális, egyenes ütközés, ilyenkor a testek mozgása a tömegközéppontjuk egydimenziós mozgásával írható le, és a forgás lehetőségével sem kell törődnünk. Az ilyen ütközéseknél mindkét test tömegpontnak tekinthető (1. ábra). 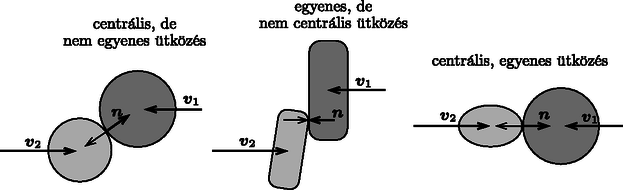  1. ábra   Az ütközések leírásánál általában nem vizsgáljuk, hogy mennyi ideig tart a folyamat, és azt sem feszegetjük, hogy rugalmatlan ütközéseknél hová tűnik az ,,elveszett'' mechanikai energia. A továbbiakban ezeket a kényes kérdéseket próbáljuk meg elemezni, de a jelenség bonyolultságára való tekintettel a lehető legegyszerűbb geometriai viszonyokat választjuk, és néhány egyszerűsítő fizikai feltevéssel is élünk. Ez utóbbiak jogosságát (vagy téves voltát) konkrét kísérletekkel, a tapasztalattal való összevetéssel dönthetjük el.   Feltevéseink: 1. Hengeres, egyenes rudak ütközését vizsgáljuk. Először egyetlen rúdnak egy merev (összenyomhatatlan) fallal, utána pedig két rúd egymással történő ütközésével foglalkozunk. 2. A rudak anyaga és a keresztmetszete megegyezik, a hosszúságuk lehet különböző. 3. A hengerek harántmérete kicsi a hosszukhoz képest. 4. A testek a hossztengelyük mentén mozognak, ütközésük (egymással vagy a fallal) centrális és egyenes. (A rudak végeit kicsit legömbölyítették, így az ütközési felületdarabka helye nem válik bizonytalanná.) 5. A hengerekben kialakuló feszültségek és deformációk a tengelyükre merőleges keresztmetszet mentén állandók (de ezen ,,állandók'' értéke a tengely mentén is és időben is változhat). 6. Az ütköző testek sebessége elhanyagolhatóan kicsi a hengerekben terjedő longitudinális hullámok (hang, lökéshullám) terjedési sebességéhez képest. 7. Az ütköző testek egymásnak csapódó felületdarabjai nem ,,pattannak'' vissza, távolságuk (és így a relatív sebességük is) egy bizonyos ideig (ez tekinthető az ütközés idejének) nulla marad. Az ütköző test (testek) egyre nagyobb része nyomódik össze, deformálódik, és emiatt benne nyomó- (esetleg húzó-) feszültségek alakulnak ki. A két test akkor válik el egymástól, amikor a feszültség előjele megváltozik, és már az érintkezés helyén is húzófeszültségnek kellene fellépnie. 8. A kialakuló rugalmas feszültség ($\sigma =F/A$) és a relatív megnyúlás ($\epsilon =\Delta \ell /\ell$) minden helyen és minden pillanatban arányos egymással: $\sigma =E\epsilon$ (ez a Hooke-törvény), ahol $E$ az anyag Young-modulusa. 9. Az ütközés (nagyon rövid) ideje alatt semmilyen ,,disszipatív'' folyamattal (külső vagy belső súrlódással, maradandó alakváltozással) nem kell számolnunk.   Ezen feltevések egyáltalán nem magától értetődőek, és bizonyos esetekben nem is teljesülnek. Amikor egy autó frontálisan ütközik egy merevnek tekinthető betonfallal vagy egy másik autóval, akkor maradandó alakváltozást szenved. Ilyenkor a deformáció és a feszültség kapcsolata nagyon eltér a Hooke-törvénytől. A gépkocsi elején és a hátulján ‐ szándékosan ‐ olyan ,,energiaelnyelő zónát'' (gyűrődő zónát) alakítanak ki, amely a mozgási energia minél nagyobb hányadát képes ,,disszipálni'', miközben az utastér lehetőleg nem károsodik jelentősen.   Megjegyzés. Kicsit általánosabb értelemben ütközési folyamatnak tekinthető az a jelenség is, amikor egy hosszú, egyenletesen haladó autósor eleje piros lámpához érkezik. Ekkor az egymást követő autók közül egyre több áll meg (a kocsisor deformálódik). A már álló és a még mozgó autókat elválasztó, képzeletbeli határvonal (lökéshullám) valamekkora sebességgel ,,halad'' hátrafelé, de az autók sebességének lecsökkenését nem a közöttük kialakuló rugalmas feszültségek, hanem a kerekek és az útburkolat közötti súrlódási erő okozza. Eközben a fékeknél (nem kívánatos esetben a megcsúszó kerekek és az aszfalt között) fellépő energiadisszipáció teszi ezt az ,,ütközési'' folyamatot rugalmatlanná.   Merev falnak ütköző rugalmas henger Térjünk rá a merev falnak ütköző, $\ell$ hosszúságú, $\varrho$ sűrűségű, $v_0$ sebességgel balra haladó rugalmas rúd (henger) esetére. Ha a megfogalmazott feltevések teljesülnek, akkor a következő történik (2. ábra ,,pillanatfelvételei''). A falnak csapódó rúd bal oldali vége $t=0$ pillanatban hirtelen megáll, és mivel a rúd többi része ekkor még $v_0$ sebességgel mozog, a bal oldalon a rúdnak egyre nagyobb része nyomódik össze. Az összenyomódott és már lefékeződött tartomány (amit az ábrákon sötétebb árnyalattal jelöltünk) egyre nagyobbá válik, mert a két tartomány határa valamekkora $c$ sebességgel mozog jobbra. Ezt a sebességet még nem ismerjük, de a Newton-féle mozgásegyenlet és a Hooke-törvény felhasználásával könnyen ki tudjuk számítani. 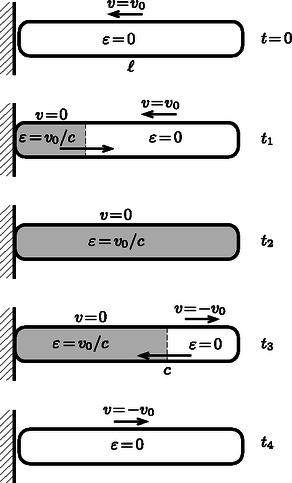  2. ábra   Tekintsük az ábrasor második képét, a $t=t_1$ pillanathoz tartozó állapotot! A lökéshullám ezideig ${\ell }_1=c{t}_1$ utat tett meg, míg az összenyomódott anyagmennyiség jobb széle $\Delta \ell =v_0{t}_1$ szakasznyit mozdult el balra. A sötétebb tartomány relatív összenyomódása: $\begin{array}{c}{\displaystyle \epsilon =\frac{\Delta \ell }{{\ell }_1}=\frac{v_0{t}_1}{c{t}_1}=\frac{v_0}{c}\ll 1.}\end{array}$ A deformáció következtében az összenyomódott anyagban rugalmas nyomófeszültség alakul ki, ennek nagysága a Hooke-törvény szerint $\begin{array}{c}{\displaystyle \sigma =E\epsilon =E\frac{v_0}{c}\mathrm{.}}\end{array}$   Megjegyzés. A Hooke-törvény alkalmazhatóságához szükséges, hogy a relatív deformáció kicsi legyen, vagyis $v\ll c$ teljesüljön. Egy acélfalnak csapódó, a hangsebességgel összemérhető (vagy azt meghaladó) sebességgel mozgó pisztolylövedékre ez a feltétel nyilván nem teljesülne, ezért az ilyen ,,henger'' nem rugalmas deformációt, hanem maradandó alakváltozást szenved el.   A rugalmas feszültség hatására az $A$ keresztmetszetű rúd $F=\sigma A$ erővel nyomja a merev falat, és a fal ugyanekkora nagyságú ellenerőt fejt ki a rúdra. Ez az erő a lefékezett anyagdarabra ható eredő erő, hiszen a sötéten jelölt tartomány jobb szélén a deformálatlan (tehát feszültségmentes) rész nem fejt ki erőt. A $t_1$ idő alatt lefékezett anyagmennyiség tömege $m=\varrho Ac{t}_1$, lendületének megváltozása tehát (abszolút értékét tekintve) $\Delta I=m{v}_0=\varrho Ac{t}_1{v}_0$. Newton törvénye szerint $\begin{array}{c}{\displaystyle F{t}_1=\sigma A{t}_1=EA\frac{v_0}{c}{t}_1=\Delta I=\varrho Ac{t}_1{v}_0\mathrm{,}\text{ahonnan}c=\sqrt[]{\frac{E}{\varrho }}\mathrm{.}}\end{array}$ Ez a (sok Olvasónak bizonyára ismerős) képlet megegyezik a rugalmas közegekben terjedő (szinuszos) longitudinális hullámok terjedési sebességét megadó összefüggéssel. A lökéshullám $t_2=\ell /c$ időpontban eléri a henger jobb szélét (2. ábra), ekkor a test minden része áll, de a deformáció miatt nyomófeszültség van benne. Ez a feszültség a henger jobb szélének egyre nagyobb darabját gyorsítja fel $-v_0$ sebességre, miközben a már mozgásba hozott és a még álló részeket elválasztó vonal $c$ sebességgel halad balra. (Úgy is mondhatjuk, hogy a lökéshullám a henger szabad végéről visszaverődik.) A $t=t_4=2\ell /c$ időpillanatban a hengeres rúd egésze feszültségmentes állapotba kerül, minden darabkájának $-v_0$ lesz a sebessége, tehát a rúd elválik a faltól, és deformációmentes és rezgésmentes állapotban mozog jobbra. Ez az ütközés tökéletesen rugalmas ($k=1$), hiszen a rúdnak a falhoz viszonyított (relatív) sebessége az ütközés után ugyanakkora nagyságú, mint amekkora előtte volt. Az ütközés teljes időtartama (vagyis az az idő, amíg a hengeres rúd a fallal érintkezett): $\Delta t=2\ell /c$.   Megjegyzés. A longitudinális hullámok terjedési sebessége fémekben néhány km/s, ez nyilván sokkal nagyobb, mint az ütköző testek tömegközéppontjának szokásos sebességértékei. Az ütközés ideje néhány centiméteres testeknél (például acélgolyóknál, biliárdgolyóknál) ${10}^{-5}$ s nagyságrendű. Ez az idő a szokásos körülmények között elhanyagolható (tehát pillanatszerűnek tekinthető), bár gyors elektronikus eszközökkel jól mérhető.   Két egyforma henger ütközése Vizsgáljuk most két egyforma (azonos keresztmetszetű, hosszúságú és sűrűségű, valamint ugyanakkora Young-modulussal rendelkező) hengeres rúd centrális, egyenes ütközését! A tömegközépponti koordináta-rendszerben a rudak sebessége ugyanakkora $v_0$ nagyságú, de ellentétes irányú. Az elrendezés szimmetriája miatt az ütközési felület mozdulatlan marad, és az egyes rudakban ugyanazok a folyamatok mennek végbe, mint a merev falnak ütköző rúdban. Lökéshullámok indulnak el az ütközési felülettől a rudak szabad végei felé. A lökéshullámok $c=\sqrt[]{E/\varrho }$ sebességgel terjednek, és a rudak végéről visszaverődve $\Delta t=2\ell /c$ idő alatt érnek vissza az ütközési felülethez. Ekkor a rudak feszültségmentes állapotban, $\pm v_0$ sebességgel indulnak tovább. A rudak relatív sebessége ugyanakkora az ütközés után, mint amekkora az ütközés előtt volt ($2v_0$). Ezek szerint az egyforma rudak ütközése is tökéletesen rugalmas: az ütközési szám $k=1$. Más lesz a helyzet akkor, ha az ütköző rudak hossza különböző. Alkalmasan választott koordináta-rendszerből nézve (ez a koordináta-rendszer nem a tömegközépponti rendszer) az ütközési felület most is mozdulatlan marad, éppen úgy, mint ahogy a merev falnál vagy az egymással ütköző, egyenlő hosszú rudaknál történt. Ebben az esetben is lökéshullámok indulnak el az ütközési felülettől, de azok nem egyszerre érkeznek vissza a kiindulási helyükre. Emiatt a rudak szétválásának pillanatában az egyikükben még mechanikai feszültségek vannak, és ennek a rúdnak az egyes darabkái a rúd tömegközéppontjához képest még mozognak. (Ez a ,,belső'' mozgás természetesen az ütközés után idővel lecsillapodik.) Adott kezdősebességek és rúdhosszak esetén kiszámítható az ütközési szám, és 1-nél határozottan kisebbnek adódik, tehát az ilyen ütközés rugalmatlan (lásd a P. 4948. számú kitűzött feladatot lapunk 317. oldalán). A különböző hosszúságú rudak ütközése ‐ a számítások szerint ‐ még abban az esetben is rugalmatlan, ha az ütközés nagyon rövid ideje alatt semmiféle olyan disszipatív folyamat (belső vagy külső súrlódás) nem működik, ami a mechanikai összenergiát csökkentené. Mégis igaz, hogy az ütközés során a tömegközéppontok sebességéhez tartozó összes mozgási energia lecsökken, mert az energia egy része az ütköző testek valamelyikének (esetleg mindkettőnek) rezgési energiájává alakul. A fenti, egyszerű modell keretei között kiszámolt ütközési számokat össze lehet hasonlítani a kísérletekben mérhető értékekkel. Szegedi Ervin hosszúkás, plexiből készült téglatesteket ütköztetett légpárnás asztalon. A sebesség mérését a testekre helyezett kis zászlókkal, fénykapukkal és számítógéppel oldotta meg. A testek megfelelő irányú mozgását (a centrális és egyenes ütközést) vezetősínekkel biztosította. (A vezetősín és a testek súrlódása természetesen szisztematikus mérési hibát okozott, ami főleg az egyenlő hosszú testek ütközésénél volt számottevő.) A különböző hosszúságú testeknél mért ütközési számok jól egyeztek az elméleti számítások eredményével.   Különböző anyagú és alakú testek ütközése Egyforma anyagú, de különböző méretű rudak ütközésénél a $k$ ütközési szám annál kisebb, minél nagyobb eltérés van az ütköző rudak hossza között. Hasonló jelenség figyelhető meg más (pl. gömb vagy korong) alakú testek ütközésénél is, bár itt az elméleti számítás lényegesen bonyolultabb, mint az ,,egydimenziós'' rudaknál. Az a jelenség, hogy az ütközés után a mechanikai energia számottevő része rezgés formájában visszamarad, tipikusnak nevezhető, és szinte kikerülhetetlen velejárója minden ütközésnek. Felmerül a kérdés: Miért létezhetnek a valóságban olyan ütközések, amelyek ‐ jó közelítéssel ‐ rugalmasnak tekinthetők? Ilyen például egy jól felfújt focilabda ütközése a játékos fejével (3. ábra), a pingponglabda és a pingpongütő ütközése, vagy a sínen guruló, könnyű rugókkal ellátott kiskocsik ütközése a fizikaórán. Ezeknél az ütköző testek nem homogén anyageloszlásúak. A labdánál a tömeget a labda fala, a rugalmasságot a benne lévő könnyű levegő biztosítja. Ugyanez az inhomogenitás a kiskocsinál és a rugónál is fellelhető. Ezen esetekben nem tud kialakulni olyan rugalmas ,,belső'' rezgés (hullámzás), ami az összenergia számottevő részét ,,ellophatná''. De még a cikkünkben tárgyalt rudak ütközése is lehet majdnem tökéletesen rugalmas, ha egy rövidebb és egy jóval hosszabb test ütközik ugyan, de a hosszabb test sokkal merevebb (nagyobb a Young-modulusa, és ezzel együtt a benne terjedő hang sebessége is sokkal nagyobb), mint a rövidebb párja.   3. ábra   1A cikkben leírtak legnagyobb része a kiváló tanár, dr. Szegedi Ervin (1957‐2006) mintegy három évtizeddel ezelőtti (egy Fizikatanári Ankéton elhangzott) előadásának gondolatmenetét követi. (G. P.)