Cím:	Megoldásvázlatok a 2016/4. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Gyanó Éva
Füzet:	2016/május, 267 - 272. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $a)$ Bizonyítsuk be, hogy az alábbi kifejezés értéke $x$-től független: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}{}^{2}x\left(\text{sin}{}^{4}x+\text{sin}{}^{2}x+2\right)+\text{cos}{}^{2}x\left(\text{cos}{}^{4}x+\text{cos}{}^{2}x+2\right)+}\hfill \\ \hfill {\displaystyle +\frac{\text{sin}{}^{2}2x}{4}\cdot \left(3\text{sin}{}^{2}x+3\text{cos}{}^{2}x+2\right)\mathrm{.}}\hfill \end{array}}$ $b)$ Számológép nélkül adjuk meg a következő kifejezés pontos értékét: $\begin{array}{c}{\displaystyle \left(1+\text{tg}{137}^{\circ }\right)\left(1+\text{tg}{136}^{\circ }\right)\left(1+\text{tg}{135}^{\circ }\right)\left(1+\text{tg}{134}^{\circ }\right)\mathrm{.}}\end{array}$ (12 pont)   Megoldás. $a)$ A zárójeleket felbontva, majd a kifejezést alakítva: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \text{sin}{}^{6}x+\text{sin}{}^{4}x+2\text{sin}{}^{2}x+\text{cos}{}^{6}x+\text{cos}{}^{4}x+2\text{cos}{}^{2}x+}\hfill \\ \hfill {\displaystyle +3\text{sin}{}^{4}x\text{cos}{}^{2}x+3\text{sin}{}^{2}x\text{cos}{}^{4}x+2\text{sin}{}^{2}x\text{cos}{}^{2}x=}\hfill \\ \hfill {\displaystyle ={\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)}^3+{\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)}^2+2\left(\text{sin}{}^{2}x+\text{cos}{}^{2}x\right)=1+1+2=4.}\hfill \end{array}}$ Az eredeti kifejezés értéke független $x$-től. $b)$ A harmadik tényező nulla, így a szorzat értéke nulla.   2. Oldjuk meg az egyenletet a valós számok halmazán: $\begin{array}{c}{\displaystyle 3\cdot \text{log}{}_8\left(x-2\right)+2\cdot \text{log}{}_4\left(2x\right)-5^{1-2\text{sin}x}\cdot \text{log}{}_2\left(2x^2-4x\right)=0.}\end{array}$ (13 pont)   Megoldás. Az egyenletnek akkor van értelme (a logaritmus miatt), ha $x>2$. Átírjuk 2-es logaritmusra az egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{3\text{log}{}_2\left(x-2\right)}{\text{log}{}_{2}8}+\frac{2\text{log}{}_2\left(2x\right)}{\text{log}{}_{2}4}-5^{1-2\text{sin}x}\cdot \text{log}{}_2\left(2x^2-4x\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{log}{}_2\left(x-2\right)+\text{log}{}_2\left(2x\right)-5^{1-2\text{sin}x}\cdot \text{log}{}_2\left(2x^2-4x\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{log}{}_2\left(2x^2-4x\right)-5^{1-2\text{sin}x}\cdot \text{log}{}_2\left(2x^2-4x\right)}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \text{log}{}_2\left(2x^2-4x\right)\cdot \left(1-5^{1-2\text{sin}x}\right)}& {\displaystyle =0.}\hfill \end{array}}$ Innen $1-5^{1-2\text{sin}x}=0$ vagy $\text{log}{}_2\left(2x^2-4x\right)=0$. Az első esetből $5^{1-2\text{sin}x}=1=5^0$, ahonnan $1-2\text{sin}x=0$, azaz $\text{sin}x=\frac{1}{2}$. Ebből $x_1=\frac{\pi }{6}+2k\pi$, $x_2=\frac{5\pi }{6}+2n\pi$. Figyelembe véve az $x>2$ kikötést: $k\in {\text{N}}^{+}$, $n\in \text{N}$. A második esetben $2x^2-4x-1=0$. Ennek gyökei: $\frac{4+2\sqrt[]{6}}{4}$, illetve $\frac{4-2\sqrt[]{6}}{4}$. A negatív gyök nem megoldás, így az eredeti egyenlet megoldásai: $x_1=\frac{\pi }{6}+2k\pi$, $k\in {\text{N}}^{+}$; $x_2=\frac{5\pi }{6}+2n\pi$, $n\in \text{N}$; $x_3=\frac{4+2\sqrt[]{6}}{4}$.   3. Egy $305$ tagú társaságból elment a nők $a\%$-a, így a társaság létszáma $\frac{a}{b}\%$-kal csökkent, ahol $1<b<305$ egész szám. Hány férfi van a társaságban?  (13 pont)   Megoldás. Jelöljük $n$-nel a 305 tagú társaságban levő nők számát. Ha elment a nők $a\%$-a, akkor a társaság létszáma $305-\frac{na}{100}$. Ezzel az egész társaság létszáma $\frac{a}{b}\%$-kal csökkent, így felírhatjuk: $\begin{array}{c}{\displaystyle 305-\frac{na}{100}=305\cdot \left(1-\frac{\frac{a}{b}}{100}\right)\mathrm{,}\frac{na}{100}=\frac{305a}{100b}\mathrm{,}\text{ahonnan}n=\frac{305}{b}\mathrm{.}}\end{array}$ Mivel $n$ pozitív egész, és $b>1$ egész, továbbá $305=5\cdot 61$, ezért csak $b=5$ vagy $b=61$ lehetséges. Ennek megfelelően a nők száma 61 vagy 5, vagyis a társaságban levő férfiak száma 300 vagy 244 fő.   4. Egy konvex sokszög oldalainak a számát megdupláztuk, így átlóinak a száma $400\%$-kal növekedett. $a)$ Hány oldalú az eredeti sokszög? $b)$ Hány százalékkal növekedett a sokszög belső szögeinek összege?  (13 pont)   Megoldás. $a)$ Ha a konvex sokszög oldalainak száma $n$, akkor átlóinak száma $\frac{n\left(n-3\right)}{2}$. Ha az oldalak számát megdupláztuk, akkor a $2n$ oldalú konvex sokszög átlóinak száma $\frac{2n\left(2n-3\right)}{2}$. Az utóbbi az előbbinek $400\%$-kal megnövelt értéke, vagyis 5-szöröse: $5\cdot \frac{n\left(n-3\right)}{2}=\frac{2n\left(2n-3\right)}{2}$, $n\ne 0$, tehát ebből $5n-15=4n-6$, $n=9$. Vagyis az eredeti konvex sokszög oldalainak száma: $n=9$. $b)$ Az eredeti sokszög belső szögeinek összege: $\left(n-2\right)\cdot 180=7\cdot {180}^{\circ }$. Az új sokszög 18 oldalú, ennek belső szögösszege: $\left(2n-2\right)\cdot {180}^{\circ }=16\cdot {180}^{\circ }$. Mivel $\frac{16\cdot 180}{7\cdot 180}\approx 2\mathrm{,}286$, ezért a belső szögek összege kb. $\mathrm{128,6}\%$-kal növekedett.   II. rész     5. Milyen görbén helyezkednek el az $y=x^2+mx+1$ $\left(m\in \text{R}\right)$ parabolák csúcspontjai (tengelypontjai)?  (16 pont)   Megoldás. A függvényt teljes négyzetté alakítva: $\begin{array}{c}{\displaystyle y={\left(x+\frac{m}{2}\right)}^2-\frac{m^2-4}{4}\mathrm{.}}\end{array}$ Ezt összehasonlítva az $\left(u;v\right)$ csúcspontú $y-v=\frac{1}{2p}{\left(x-u\right)}^2$ parabolaegyenlettel a következőt kapjuk a csúcspont koordinátáira: $u=-\frac{m}{2}$, $v=-\frac{m^2-4}{4}$. A $\begin{array}{c}{\displaystyle v=-\frac{m^2-4}{4}=-{\left(\frac{m}{2}\right)}^2+1=-{\left(-\frac{m}{2}\right)}^2+1}\end{array}$ átalakítás után megállapítható, hogy $u=-\frac{m}{2}$ és $v=-{\left(-\frac{m}{2}\right)}^2+1$. Ez $\left(-\frac{m}{2}\right)$-re másodfokú, tehát parabola, egyenlete: $y=-x^2+1$. A keresett ponthalmaz tehát parabola, egyenlete $y=-x^2+1$.   6. Egy egyetem I. évfolyamán a nappali tagozatos hallgatók $20\%$-a jelesre vizsgázott analízisből. A levelező tagozaton $30\%$, míg a távoktatásban $10\%$ volt a jelesek aránya. Az egyes tagozatok létszámáról tudjuk, hogy kétszer annyi távoktatásban részt vevő van, mint levelező, és a nappalisok és a távoktatásban részt vevők száma egyenlő. $a)$ Véletlenszerűen választva egy hallgatót, mekkora az esélye, hogy analízis jegye jeles? $b)$ Ha a véletlenül választott hallgató analízis jegye jeles, akkor mi az esélye, hogy ő nappalis? $c)$ A $b)$-beli feltétel mellett mi az esélye, hogy levelező, illetve távoktatásban szereplő hallgató az illető?  (16 pont)   Megoldás. $a)$ A levelezős diákok száma $x$, a nappalis, illetve a távoktatásban tanulóké pedig $2x$. A nappalisok közül $0\mathrm{,}2\cdot 2x=0\mathrm{,}4x$ tanuló jelest, míg $0\mathrm{,}8\cdot 2x=1\mathrm{,}6x$ tanuló nem jelest kapott. A levelezősök közül $0\mathrm{,}3x$ diák jelest, és $0\mathrm{,}7x$ diák más jegyet kapott. Végül, a távoktatós hallgatók közül $0\mathrm{,}1\cdot 2x=0\mathrm{,}2x$ diák kapott jelest, $1\mathrm{,}8x$ diák pedig egyéb érdemjegyet. Az összes hallgatók száma $5x$. A kedvező esetek száma: $0\mathrm{,}4x+0\mathrm{,}3x+0\mathrm{,}2x=0\mathrm{,}9x$. A kérdezett valószínűség: $\begin{array}{c}{\displaystyle P=\frac{\text{kedvező}}{\text{összes}}=\frac{0\mathrm{,}9x}{5x}=0\mathrm{,}18.}\end{array}$ $b)$ Az összes jelest kapott hallgató száma $0\mathrm{,}9x$. A nappali tagozatos, jelest kapott (ami most a kedvező eset) diákok száma pedig $0\mathrm{,}4x$. A valószínűség: $\begin{array}{c}{\displaystyle P=\frac{\text{kedvező}}{\text{összes}}=\frac{0\mathrm{,}4x}{0\mathrm{,}9x}=\frac{4}{9}\mathrm{.}}\end{array}$ $c)$ Távoktatásban $0\mathrm{,}2x$ diák kapott jelest, tehát $\begin{array}{c}{\displaystyle P=\frac{0\mathrm{,}2x}{0\mathrm{,}9x}=\frac{2}{9}\mathrm{.}}\end{array}$ Mivel $0\mathrm{,}3x$ levelező hallgató kapott jelest, azért $\begin{array}{c}{\displaystyle P=\frac{0\mathrm{,}3x}{0\mathrm{,}9x}=\frac{3}{9}=\frac{1}{3}\mathrm{.}}\end{array}$   7. $a)$ Határozzuk meg $n\to \infty$ esetén az $\begin{array}{c}{\displaystyle a_n=\frac{2n^2+3n-1}{n^2+4}}\end{array}$ sorozat határértékét, s azt az $n$ számot, amelytől kezdve a sorozat elemei a sorozat határértékétől $\frac{1}{200}$-nál kisebb értékkel térnek el. $b)$ Bizonyítsuk be teljes indukcióval, hogy $6\mid n^3+5n$, ha $n$ pozitív egész szám.  (16 pont)   Megoldás. $a)$ ${\displaystyle A}=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{2n^2+3n-1}{n^2+4}=\underset{n\to \infty }{\overset{}{\text{lim}}}\frac{2+\frac{3}{n}-\frac{1}{n^2}}{1+\frac{4}{n^2}}=2$. A sorozat határértéke 2. Meg kell állapítani, hogy milyen $n$-től kezdve lesz $|a_n-A|<\frac{1}{200}$, azaz $\begin{array}{c}{\displaystyle \left|\frac{2n^2+3n-1}{n^2+4}-2\right|<\frac{1}{200}\mathrm{.}}\end{array}$ Elvégezve az összevonásokat: $\left|\frac{3n-9}{n^2+4}\right|<\frac{1}{200}$. Mivel $n>3$ esetén a bal oldal pozitív, ezért az abszolút érték jele elhagyható: $\frac{3n-9}{n^2+4}<\frac{1}{200}$. Az egyenlőtlenséget rendezve kapjuk: $n^2-600n+1804>0$. Az $n^2-600n+1804=0$ egyenletet megoldva kapjuk, hogy $n_1\approx 3\mathrm{,}02$ és $n_2\approx 596\mathrm{,}98$. Sorozatról van szó, így csak $n\ge 597$ lehet a megoldás. $b)$ Az állítást $n=1$-re felírva: $1+5=6$, ami nyilván osztható 6-tal, tehát $n=1$-re az állítás igaz. Tegyük fel, hogy $k=n$ esetén teljesül, hogy $6\mid k^3+5k$. Írjuk fel a kifejezést $n=k+1$-re: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(k+1\right)}^3+5\left(k+1\right)=k^3+3k^2+3k+1+5k+5=\left(k^3+5k\right)+\left(3k^2+3k\right)+6.}\hfill \end{array}}$ Az $k^3+5k$ az indukciós feltétel miatt osztható 6-tal. $3k\left(k+1\right)$ a 3 miatt osztható 3-mal, a $k\left(k+1\right)$ pedig két egymást követő természetes szám szorzata és így osztható 2-vel. A kifejezés tehát három 6-tal osztható tag összege, így osztható 6-tal. A bizonyítást befejeztük.   8. 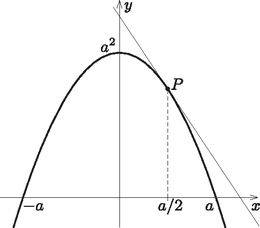Az $f\left(x\right)=-x^2+a^2$ $\left(a>0\right)$ függvény görbéjének $x$ tengely fölötti részét körbeforgatjuk az $x$ tengely körül ${360}^{\circ }$-kal. A keletkezett forgástest térfogata az $a$ sugarú gömb térfogatának kétszerese. $a)$ Határozzuk meg az $a$ paraméter értékét. $b)$ Mekkora területű háromszöget vág le a koordinátatengelyekből a függvény $x=\frac{a}{2}$ helyhez tartozó érintője?  (16 pont)   Megoldás. A függvény képe egy lefelé nyíló parabola, melynek zérushelyei $a$-ban és $\left(-a\right)$-ban vannak, az $y$ tengelyt pedig $a^2$-ben metszi.     $a)$ Az $x$ tengely feletti rész $x$ tengely körüli ${360}^{\circ }$-os elforgatottjának térfogata: $\begin{array}{c}{\displaystyle V=\pi \underset{-a}{\overset{a}{\int }}{f}^2\left(x\right)dx\mathrm{.}}\end{array}$ A szimmetria miatt az integrált elég kiszámítani a $\left[0;a\right]$ intervallumban, és a kapott eredmény kétszeresét venni: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V}& {\displaystyle =2\pi {\int }_0^a{\left(-x^2+a^2\right)}^{2}dx=2\pi \underset{0}{\overset{a}{\int }}\left(x^4+a^4-2x^2{a}^2\right)dx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =2\pi {\left[\frac{x^5}{5}+a^{4}x-2a^2\frac{x^3}{3}\right]}_0^a=2\pi \left(\frac{a^5}{5}+a^5-\frac{2}{3}{a}^5\right)=\frac{16a^5\pi }{15}\mathrm{.}}\hfill \end{array}}$ A feltétel szerint ez a térfogat az $a$ sugarú gömb térfogatának kétszerese, vagyis $\frac{16a^5\pi }{15}=\frac{8a^3\pi }{3}$, amiből $a^2=\frac{5}{2}$, és így $a=\sqrt[]{\frac{5}{2}}$ $\left(a>0\right)$. $b)$ Az $\frac{a}{2}$ abszcisszájú $P$ pont koordinátái $P\left(\frac{a}{2};f\left(\frac{a}{2}\right)\right)$, azaz $P\left(\frac{a}{2};\frac{3}{4}{a}^2\right)$. Az érintő $m$ meredeksége az $x=\frac{a}{2}$ helyen vett differenciálhányados értéke. Mivel $f\text{'}\left(x\right)=\left(-x^2+a^2\right)\text{'}=-2x$, ezért $m=f\text{'}\left(\frac{a}{2}\right)=-2\cdot \frac{a}{2}=-a$. Az érintő egyenlete: $y-\frac{3}{4}{a}^2=-a\left(x-\frac{a}{2}\right)$. Ez az érintő az $x$ tengelyt az $\left(x_1;0\right)$ pontban, az $y$ tengelyt a $\left(0;y_1\right)$ pontban metszi, és így $y_1-\frac{3}{4}{a}^2=\frac{a^2}{2}$, illetve $-\frac{3}{4}{a}^2=-a{x}_1+\frac{a^2}{2}$. Ebből pedig $y_1=\frac{5}{4}{a}^2$, valamint $x_1=\frac{5}{4}a$ következik. Így a derékszögű háromszög területe: $T=\frac{x_1{y}_1}{2}=\frac{25}{32}{a}^3$ területegység.   9. Négy egész szám közül az első három egy számtani, az utolsó három egy mértani sorozat három szomszédos eleme. A két középső szám összege $50$, a két szélső szám összege $55$. Melyik ez a négy szám?  (16 pont)   Megoldás. Legyen a négy szám: $a$, $b$, $c$, $d$. A feltételek alapján: ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle \frac{a+c}{2}}& {\displaystyle =b\mathrm{,}}\hfill & \text{(<mn>1</mn>)}\\ \hfill {\displaystyle c^2}& {\displaystyle =bd\mathrm{,}}\hfill & \text{(<mn>2</mn>)}\\ \hfill {\displaystyle a+d}& {\displaystyle =\mathrm{55,}}\hfill & \text{(<mn>3</mn>)}\\ \hfill {\displaystyle b+c}& {\displaystyle =50.}\hfill & \text{(<mn>4</mn>)}\end{array}}$ Ez utóbbiból $b=50-c$ következik. Ezt (1)-be helyettesítve: $\frac{a+c}{2}=50-c$, vagyis $a=100-3c$. A kapott eredményt (3)-ba írva: $100-3c+d=55$, vagyis $d=3c-45$. A részeredményeket (2)-be helyettesítve kapjuk: $c^2=\left(50-c\right)\left(3c-45\right)$. Rendezés után: $4c^2-195c+2250=0$. Ennek megoldásai: $c_1=30$, $c_2=18\mathrm{,}75$. A feladat értelmében egész számokat keresünk, így csak a $c=30$ lehet a megoldás. Így a négy szám: 10, 20, 30, 45, amelyek megfelelnek a feltételnek.