Cím: Egyensúly, ciklus és káosz dinamikus rendszerekben
Szerző(k):  Simonovits András 
Füzet: 2016/május, 258 - 267. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1

 
1. Bevezetés

A matematikai definíciót megelőlegezve, diszkrét idejű dinamikus rendszerről beszélünk, ha a természetes számokkal jelzett időpontokban a rendszer valós számmal vagy számegyüttessel (vektorral) jellemzett állapota megadja a rendszer állapotát a következő időpontban. (Szemléletünknek jobban megfelelne a folytonos idő, de matematikai elemzése túlmutatna a középiskolai kereteken.) ``Definíciónkból'' logikailag az is következik, hogy bármennyi időszakkal előre ki tudjuk számítani a rendszer állapotát. Például ha tudjuk, hogy ma délben hol volt a Nap az égbolton, akkor azt is tudni fogjuk, hogy hol lesz a Nap holnap délben. Ebből logikailag az is következik, hogy bármennyi nappal előre meg tudjuk jósolni a Nap déli 12 órai helyzetét.
Egyszerű rendszerről beszélünk, ha az állapotváltozást leíró, ún. állapotegyenlet matematikailag ``egyszerű''. Találó fizikai példa az egyszerű és a bonyolult dinamikai rendszerre: a Föld Nap-körüli pályája, illetve az örvény. Újabb fogalmat definiálva, azt mondjuk, hogy a rendszer előrejelezhetően viselkedik, ha a kezdőállapot mérésénél elkövetett parányi hiba ellenére időben elég sokáig jól (viszonylag pontosan) előre tudjuk jelezni az állapotot.
Első látásra azt gondolhatnánk, hogy bármely egyszerű dinamikus rendszer viselkedése előrejelezhető. Ebben az írásban egyszerűen, de szabatosan próbáljuk elmagyarázni, hogy ez csak bizonyos rendszereknél igaz; de más, ugyancsak egyszerű rendszereknél nincs így. Például a Nap vagy a Föld helyzetének előrejelzésénél igaz, de a kettősingánál vagy az időjárás nagyon leegyszerűsített modelljénél nem. A döntő különbséget a jelen állapotot a következő állapotba átvivő leképezés nemlinearitása okozza.
Ragyogó népszerűsítő leírást ad a témakörről Gleick [2]. Röviden utalunk arra, hogy a középiskolás Olvasó gyakran látott már kaotikus vagy ahhoz hasonló dinamikával készített fraktálokat, ezzel azonban csak cikkünk végén, érintőlegesen foglalkozunk.
 
2. Lineáris dinamikus rendszerek

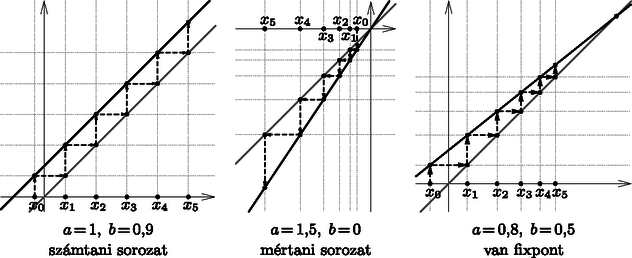
A matematikai tárgyalásra térve definiálunk egy diszkrét idejű, időben változatlan működésű, lineáris skaláris dinamikus rendszert. Legyen x egy [0,1]-beli valós szám, amely a rendszer állapotát jelképezi, t=0,1,2,... pedig az időpontok indexe. Lineáris rendszerünk állapotegyenletét egy lineáris függvény adja:
xt+1=axt+b,t=1,2,...,(1)
ahol a és b két valós szám, és az x0 kezdőállapot adott. Ez az állapotegyenlet a számtani sorozat (a=1), illetve a mértani sorozat (b=0) közös általánosítása.
Lineáris rendszernek, ha létezik ú.n. egyensúlyi helyzete: x∘, akkor az a leképezés fixpontja:
x∘=ax∘+b.(2)


 
 

 

Az (1) által leírt rendszernek csak akkor nem létezik egyensúlyi helyzete, ha a=1 és b≠0. Ez a leképezés a jól ismert számtani sorozat, amelynek explicit megoldása xt=x0+bt, amely nyilvánvalóan a végtelenbe tart. A továbbiakban ezt általában kizárjuk.
 
1. tétel. a) Ha a≠1, akkor az (1) lineáris rendszer egyensúlyi helyzete létezik és értéke
x∘=b1-a.

b) Ekkor a megoldás explicite a következőképpen adható meg:
xt-x∘=at(x0-x∘),t=1,2,....(3)

 
Bizonyítás. Vonjuk ki az (1) egyenletből a (2) egyenletet: xt+1-x∘=a(xt-x∘). A mértani sorozat képlete szerint adódik (3).  □
 
A (3) segítségével érdekes megfigyelések tehetők a lineáris rendszer viselkedéséről. a) A (3) megoldás akkor és csak akkor korlátos, ha |a|<1 vagy a=-1. b) a=-1 esetén a (3) egyenlet 2-ciklust ad: x1=-x0+b és x2=x0 (fűrészfog). A továbbiakban feltesszük, hogy |a|<1. c) Ekkor minden közeli x0 esetén xt közel marad x∘-hoz: stabilitás. d) Az xt állapot tart x∘-hoz minden x0 esetén: aszimptotikus stabilitás. (Mellesleg a korábban már kizárt a=-1-re a c) teljesül, de d) nem teljesül.) e) Legyen egy másik pálya yt+1=ayt+b, kivonva egymásból a két egyenletet: yt+1-xt+1=a(yt-xt), tehát a közelről induló pályák közel maradnak egymáshoz. (Mellesleg ez a tulajdonság a korábban már kizárt a=1-re is igaz.)

 
 

Az 1. táblázat a legfontosabb pályatípusokat mutatja be konkrét számpéldákon. Az áttekinthetőség kedvéért az állapotok értékét 3 tizedesjegyre kerekítve adjuk meg, de ennél több értékes jegyre számolunk.
Számtani sorozat: xt+1=xt+1, nem korlátos. Fűrészfog: xt+1=-xt, 2-ciklus, amely stabil, de nem aszimptotikusan stabil. Eltűnő sorozat: xt+1=0,5xt, aszimptotikusan stabil. A kezdőállapot mindhárom esetben 1.
 
1. táblázat. Három pályatípus
 
Idő    Számtani sorozat  Fűrészfog    Eltűnő sorozatt   xt   yt                zt   0    1  1              1    1    2  -1              0,500    2    3  1              0,250    3    4  -1              0,125    4    5  1              0,063    5    6  -1              0,031  
 

A továbbiak szempontjából érdekes, hogy a lineáris leképezés mikor hagyja helyben a [0,1] szakaszt. Az |a|<1 eseten belül két alesetet kell megkülönböztetnünk: 0≤a<1 esetén a [0,1] szakasz a [b,a+b] szakaszba képződik le, amely akkor része [0,1]-nek, ha b≥0 és a+b≤1. -1<a<0 esetén a [0,1] szakasz az [a+b,b]-be képződik le, amely akkor része [0,1]-nek, ha a+b≥0 és b≤1.
 
3. Nemlineáris dinamikus rendszerek

Egyszerűségük miatt a lineáris rendszerek modelljei nagyon gyakran nagyon hasznosak, de máskor túl kell lépnünk rajtuk (vö. Simonovits [2]). Például olyan korlátos rendszert vizsgálunk, amely nem stabil. Ehhez szükségünk van egy f függvényre, amely a [0,1] szakaszt önmagába képezi le. A dinamikus rendszer mozgását, az állapotváltozást az állapotegyenlet írja le:
xt+1=f(xt),t=0,1,2,...,T,x0   adott.(4)
Feltehetjük, hogy az f függvény folytonos, azaz közeli kezdőállapotokból induló pályák az első időszakban is közel maradnak egymáshoz. A folytonosságnak egy speciális alakját választva, feltesszük, hogy van olyan L>0 állandó, amelyre a képpontok távolsága legfeljebb L-szerese a tárgypontokénak:
|f(x)-f(y)|≤L|x-y|   minden  (x,y)   párra.(5)
Lineáris leképezésnél (5)-ben például L=|a| megfelelő.
Azt, hogy ez a feltevés nem minden folytonos függvényre teljesül, a [0,1] szakaszon definiált f(x)=x négyzetgyök-függvény példája mutatja. Valóban, az x=0 és y≠0 pontpár esetén a kép- és a tárgypontok távolságának az aránya,
f(y)-f(x)y-x=1y
a 0 közelében nem korlátos.
(4)-ben egymás után elvégezve a behelyettesítéseket, a t-edik időszak állapota elvileg egyszerű függvénye marad a kezdőállapotnak, de a lineáris esettel ellentétben, általában nincs explicit megoldás. Teljes indukcióval (5)-ből könnyen levezethető, hogy a szomszédos (egymáshoz közeli x0 kezdőértékkel rendelkező) pályákra teljesül
|yt-xt|≤Lt|y0-x0|,t=1,2,...,T.(6)

Ha csak adott T-ig vagyunk kiváncsiak az eltérésre, akkor akármilyen nagy is L, (6) jobb oldala is korlátos marad. Ahhoz viszont, hogy akármekkora T-re korlátos maradjon az eltérés, (6) értelmében az L≤1 egyenlőtlenséget kellene feltennünk. Megelégszünk egy lazább definícióval.
Előrejelezhetőségről beszélünk vagy azt mondjuk, hogy a rendszer érzéketlen az x0 kezdőértékre, ha megfelelően közeli kezdőállapotból induló pályák mindvégig megfelelően közel maradnak. Például mégha 1 perc hibával mérjük a delet, akkor sem veszítjük szem elől a Nap pályáját az égbolton vagy a Föld pályáját a Nap körül. Ugyanilyen jól előrejelezhetjük az ágyúból kilőtt golyó pályáját.
A lineáris rendszerekben bevezetett egyensúlyi helyzet általánosítható a nemlineáris rendszerekre. Képletben: x∘ egyensúlyi helyzet, ha x∘=f(x∘). Hamarosan látni fogjuk, hogy adott rendszernek létezhet több egyensúlyi helyzete is.
Már a lineáris rendszer tárgyalásakor láttuk, hogy egy egyensúlyi helyzet vagy stabil vagy instabil. Matematikai szabatosságról lemondva, azt mondjuk, hogy az x∘ egyensúlyi helyzet lokálisan stabil, ha minden, hozzá elég közeli kezdőállapotból induló pálya közel marad. Már a lineáris esetben utaltunk az erősebb stabilitás fogalomra is, amelyet lokális aszimptotikus stabilitásnak nevezünk: a közeli kezdőállapotból induló pályák nemcsak közel maradnak, hanem aszimptotikusan tartanak az egyensúlyi helyzethez. Globálisan aszimptotikusan stabilnak nevezzük a rendszert, ha az aszimptotikus közelítés tetszőleges kezdeti állapotra igaz. (Például a pincér tálcáján billegő tányér helyzete csak lokálisan stabil, de globálisan nem.)
Ha (5)-ben L<1 áll, akkor a leképezést kontrakciónak (zsugorításnak) nevezik, s ez szavatolja az egyensúlyi helyzet egyértelműségét és globális aszimptotikus stabilitását.
Könnyű belátni, hogy a lineáris rendszerekhez hasonlóan a nemlineáris rendszerekben is igaz a következő állítás:
 
2. tétel. Ha egy egyensúlyi állapot stabil, akkor a (4) rendszer összes pályája érzéketlen az egyensúlyhoz közeli kezdeti feltételekre.
 
Bizonyítás. Valóban, a két pálya távolsága
yt-xt=yt-x∘+x∘-xt
alapján becsülhető:
|yt-xt|≤|yt-x∘|+|x∘-xt|.(7)
A stabilitás miatt (7) jobb oldalán mindkét tag kicsi, tehát összegük is az.  □
 
Talán a legegyszerűbb nemlineáris függvény a logisztikus függvény, és az általa létrehozott dinamikus rendszer kiváló gyakorlóterep a vizsgálatokra:
xt+1=axt(1-xt).(8)
Könnyű belátni, hogy 0<a≤4 esetén a logisztikus leképezés a [0,1] szakaszt a [0,1] szakaszba képezi le.
A következőkben e leképezés paraméter-intervallumát leszűkítjük: 1<a≤4, s az általa definiált dinamika egyensúlyi helyzetét és stabilitását, illetve annak hiányát elemezzük.
Helykímélés céljából közös táblázatban mutatjuk be a négy különböző paraméterértékre, de azonos kezdőértékre vonatkozó dinamikát (az 5 paraméterérték a táblázatban látható). Az xt(a) jelölés a paramétertől való függésre utal. A pályák elnevezése csak később válik világosabbá.
 
2. táblázat. Különböző paraméterű logisztikus pályák
 
A s z i m p t o t i k u s a n  Idő    stabil    2-ciklikus  3-ciklikus    Kaotikust   xt(2)   xt(3,2)   xt(3,839)   xt(4)0    0,140    0,140    0,140    0,140    1    0,241    0,385    0,462    0,482    2    0,366    0,758    0,954    0,999    3    0,464    0,587    0,168    0,005    4    0,497    0,776    0,535    0,022    5    0,500    0,557    0,955    0,084    6    0,500    0,790    0,165    0,309    7    0,500    0,531    0,529    0,853    8    0,500    0,797    0,956    0,500    9    0,500    0,518    0,160    1,000    10    0,500    0,799    0,516    0,000    11    0,500    0,514    0,959    0,000    12    0,500    0,799    0,152    0,000    13    0,500    0,513    0,494    0,000    14    0,500    0,799    0,960    0,001    15    0,500    0,513    0,149    0,003  
 

A 2. táblázat 1. pályája aszimptotikusan stabil, már a t=5 időszakban eléri az egyensúlyi helyzetet (legalábbis az első 3 tizedesjegyben). Ezt általánosítja a
 
3. tétel. a) 1<a≤4 esetén a (8) logisztikus rendszer egyensúlyi helyzete
x∘=a-1a∈(0,1).

b) 1<a≤3 esetén az x∘ egyensúlyi helyzet ‐ kivételes kezdőállapotoktól eltekintve ‐ globálisan aszimptotikusan stabil, 3<a≤4 esetén nem.
 
Bizonyítás. a) pontja triviális, a b) pontja is igazolható, de ettől eltekintünk.  □
 

Valójában a logisztikus leképezésnek még egy egyensúlyi helyzete van, a triviális 0 pont, ettől azonban eltekintünk. Nemcsak az onnan, de az 1-ből induló pálya is 0-ba ugrik, és ott is marad.
A természetben számos dinamikus rendszer pályája ismétlődik. Például a Nap körül keringő Föld (kerekítve) 365 naponként visszatér eredeti helyzetébe. A szívverés és a légzés is periodikus. Diszkrét idejű rendszerben egy P>1 természetes szám esetén P-ciklusról beszélünk, ha az f leképezés hatására keletkező (xt) pálya P időszakonként ismétlődik. Formálisan: az (x1,x2,...,xP) vektort P-ciklusnak nevezzük, ha teljesül a következő egyenlőségsorozat:
x2=f(x1),...,xP=f(xP-1)ésx1=f(xP).
Ebből következik, hogy folytatáskor tetszőleges természetes k-ra xPk+r=xr, r=1,2,...,P. Elfajult eseteket kizárandó feltesszük, hogy a nevezett vektor minden eleme különböző.
A lineáris esetben már találkoztunk a fűrészfog-ciklussal. Ez a ciklus az egyenesnek az origóra való tükrözéséből adódik, és nem túl érdekes. Annál érdekesebb viszont a 2. táblázat 2. pályája, amely a t=12. időszakban visszatér a két időszakkal korábbi helyzetébe, és ez rendületlenül ismétlődik. Ezt fejezi ki általánosabban is a
 
4. tétel. A (8) logisztikus leképezésnek van 2-ciklusa, ha 3<a≤4.
 
Bizonyítás. Egyelőre tegyük föl, hogy valóban van 2-ciklus, jele (x1,x2). Ekkor igaz, hogy
x2=ax1(1-x1)ésx1=ax2(1-x2).
Behelyettesítve a második egyenletet az elsőbe (vagy fordítva):
xr=a[axr(1-xr)][1-axr(1-xr)],r=1,2.
Negyedfokú egyenletet kaptunk, amelynek egyik gyöke x3=0, a másik gyöke a 3. tételbeli fixpont: x4=(a-1)/a. Elhagyva az indexet, először elosztjuk az egyenletet x-szel:
a3x3-2a3x2+a2(1+a)x+1-a2=0.
A kapott harmadfokú egyenletet (x-x4)-gyel osztva, egy másodfokú egyenletet kapunk:
a2x2-a(a+1)x+a+1=0.
Az ismert megoldóképletet alkalmazva megkapjuk a feltételezett 2-ciklust:
x1,2=(a+1)±(a+1)(a-3)2a.(9)
A megadott paraméterszakaszon 0<x1,2<1.
Figyeljük meg, hogy ha felülről közelítjük a=3-at, akkor a 2-ciklus mindkét eleme az eltűnő diszkrimináns miatt az éppen instabillá váló egyensúlyi helyzethez tart. Fordítva haladva, azt mondjuk, hogy az egyensúlyi helyzet kettéágazik.  □
 

Megjegyzések. 1. Magasabb matematikai eszközökkel belátható, hogy 3<a<1+6=3,44... esetén a kivételektől eltekintve, akármilyen kezdőállapotból indítsuk is e rendszert, a pálya aszimptotikusan tart az itt megadott 2-ciklushoz. Az egyensúlyi állapot azonban instabil, és kivételesen itt érzékenyen függ a pálya a kezdőfeltételtől.
2. Természetesen figyelembe kell venni, hogy (x2,x1) is geometriailag ugyanezt a 2-ciklust adja meg, mint (x1,x2).
 
2. példa. Ha a paraméterérték növelése miatt a (9)-beli 2-ciklus instabillá válik, akkor (8)-nak még létezik más ciklusa is, csak nincs rá explicit képletünk. A 2. táblázat 3. pályája egy 3-ciklushoz tart, amelynek pontjai 6 tizedesjegyre:
x1=0,149888;x2=0,489172ésx3=0,959299.
Sőt, ez a ciklus globálisan stabil: kivételes kezdőértékektől eltekintve, az összes pálya rátekeredik e ciklusra.
 

Egy meglepő tétel (Sarkovszkij, 1963) szerint a 3-ciklus létezéséből következik, hogy akármilyen P>1 egészre P-ciklus is létezik. Persze, a 2. példában ezek a ciklusok a 3-ciklus kivételével instabilak. Az 1. ábra azt mutatja meg, hol helyezkedik el a rendszer a 100. időszakban, ha egymás után a [0,1] szakaszon egyenletes távolságban elhelyezkedő 99 pontot választjuk kezdőállapotnak: x0=0,01;0,02;...;0,99. Az 1. ábra tanúsága szerint a 99 pálya mindegyike a 100. időszakban már az 1., a 2. és a 3. cikluspont valamelyikéhez olyan közel ért, hogy az eltérés szabad szemmel már nem is látható: globális stabilitás. (Ez a konvergencia már 20 időszak alatt is majdnem végbemegy.) Ugyanakkor, ha azt kérdezzük, hogy a 3 pont közül melyik közelébe ér az adott kezdőállapotból induló pálya a 100. időszakban, akkor nagyon bonyolult a válasz. Az így osztályozott kezdőállapotok a [0,1] szakaszon szeszélyesen helyezkednek el. Ezeket a halmazokat nevezte el 1985 körül Mandelbrot fraktálnak, de már 1830 körül megjelentek a matematikában, csak sokáig búvópatakként csordogáltak.


 

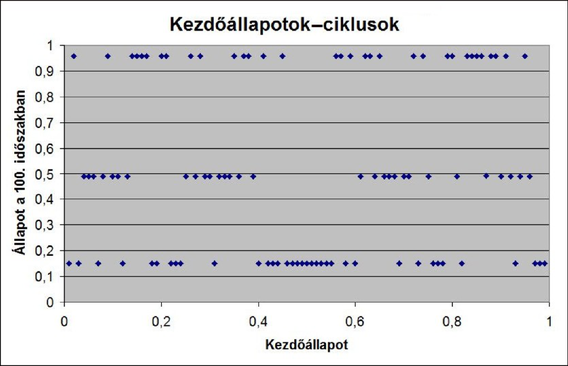1. ábra. Melyik cikluspont közelében lesz a rendszer a 100. időszakban?
 

 
4. Kaotikus viselkedés

Van, aki már a 2. példát is kaotikusnak nevezi (erre utal a ``3-ciklus káoszt implikál'' Li‐Yorke-tétel, 1973). Mi azonban szigorúbbak vagyunk, ebben az esetben csak átmeneti káoszról beszélünk, hiszen véges időn belül a stabil ciklus környékére érve a további út már előrejelezhető.
A következőkben már valóban megérkezünk a címben szereplő kaotikus viselkedés világába. Nemcsak azt látjuk be, hogy a=4-re a logisztikus rendszer mindenütt érzékeny a kezdőfeltételre, azaz előrejelezhetetlen, hanem tovább is lépünk: akármennyi idő eltelte után megmarad a határozatlanság, azaz a további pálya érzékenyen függ az xt állapottól. A 2. táblázat 4. pályája valóban szeszélyesen viselkedik: 3 tizedesjegyre kerekítve (de több tizedesjeggyel számolva), a pálya a t=9 időszakban 1, utána 4 időszakon keresztül a triviális egyensúlyi helyzetben (legalábbis annak nagyon közeli környezetében) rejtőzik, majd a 14. és a 15. időszakban újra nőni kezd. Ez is a kezdeti értéktől való érzékeny függőséget mutatja.
 
5. tétel. Az xt+1=4xt(1-xt) leképezés esetén a dinamika mindenütt érzékeny a kezdőfeltételre.
 
Bizonyítás. A dinamikát az xt=sin2φt transzformáció segítségével vizsgáljuk meg. Felhasználva a sin2φ=2sinφcosφ képletet, egyszerű számolással adódik sin2φt+1=sin22φt, azaz elhagyva a 2π vagy többszörösnyi eltéréseket,
φt+1≡2φt.
Legyen a szomszédos pálya yt+1=4yt(1-yt). Az yt=sin2ψt jelöléssel,
ψt+1≡2ψt.
A két szögdinamika eltérése 0<ψt-φt<π esetén ψt+1-φt+1=2(ψt-φt) stb. az L=2 éles korlát miatt a dinamika kaotikus.
Az 1. ábrán szereplő 99 kezdőállapotból indítva kaotikus rendszerünket, még a 100. időszakra sem világos, hol lesz a rendszer.


 

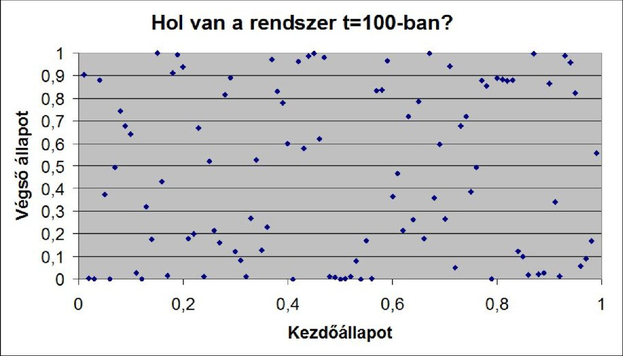2. ábra. Hol lesz a kaotikus rendszer a 100. időszakban?
 

Az, hogy általában milyen bonyolult kérdésről van szó, jól mutatja, hogy nem tudjuk megmondani, hogy a=4-en kívül mikor kapunk még kaotikus viselkedést. Csak az ismert, hogy a kaotikus pályát adó a paraméterek "sokan" vannak, és a [3,57...,4] szakaszon helyezkednek el.
Természetesen sok más kaotikus rendszer létezik, például az ún. sátorleképezés, ahol
f(x)={2x,ha  0≤x≤1/2;2-2x,ha  1/2<x≤1.

 
5. Összefoglalás

Ebben a cikkben a diszkrét idejű skalár dinamikus rendszert tanulmányoztuk. Megvizsgáltuk az egyensúlyi helyzet létezését és stabilitását. Példát mutattunk 2- és 3-ciklusokra. Végül bemutattunk egy olyan rendszert, amely előrejelezhetetlenül működik: kaotikusan viselkedik. A lehető legegyszerűbb rendszerekre szorítkoztunk, s eltekintettünk a többváltozós, több időszaki késleltetésű rendszerek elemzésétől. A folytonos idejű rendszerek vizsgálata is fontos lenne, de meghaladná kereteinket.
 
Hivatkozások

[1]Gleick, J. (1988): A káosz. Egy új tudomány születése. Magyar fordítás: Bp. Göncöl Kiadó, 1999.
[2]Simonovits, A.: Szakaszokon értelmezett leképezések fixpontjairól, KöMaL, 5 (2012), 264‐273.

"sokan"
1Köszönetet mondok Garay Barnabásnak értékes megjegyzéseiért.