Cím: Gráfalgoritmusok 6.
Szerző(k):  Schmieder László 
Füzet: 2016/április, 225 - 227. oldal  PDF  |  MathML 
Hivatkozás(ok):2016/március: Gráfalgoritmusok 5.
2015/október: Gráfalgoritmusok 1.
2015/november: Gráfalgoritmusok 2.
2015/december: Gráfalgoritmusok 3.
2016/február: Gráfalgoritmusok 4.
2016/május: Gráfalgoritmusok 7.

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az előző számokban megjelent cikkekben megvizsgáltunk néhány olyan feladatot, amelynek ábrázolása gráfokkal történt, és a megoldáshoz gráfok különféle bejárásait alkalmaztuk. A most következő részben egy olyan hétköznapi, gyakorlati problémát vizsgálunk meg, amely szintén reprezentálható gráfokkal, és a megoldást is egy gráfalgoritmus adja.

 
1. probléma. Adott egy térkép, amely helységeket és az azokat összekötő autóutakat ábrázolja. Ismerjük a térkép alapján, hogy mely helységek között vannak utak, illetve hogy az egyes utak milyen hosszúak. Adjuk meg az utak egy olyan sorozatát (ha van), amely egy kiindulási helyről valamely cél helyre vezet, és a lehető legkevesebb az így megtett utak összes hosszúsága.
 
2. probléma. Egy ország városai között repülőjáratokkal lehet közlekedni. Tudjuk, hogy mely városok között vannak járatok, illetve hogy ezek a járatok mennyibe kerülnek. Adjunk meg egy olyan útvonalat (ha van), amelyen a lehető legkevesebb költséggel lehet eljutni az Start városból a Cél városba.
 
Mindkét problémánál nyilvánvaló, hogy gráfokról van szó, és a feladat egy optimális útvonal megkeresése két adott csúcs között. A gráf annyiban különbözik a korábban megismertektől, hogy minden élhez tartozik egy szám, amelyet az él súlyának szokás nevezni. A konkrét feladattól függően a két csúcs közötti súly leírja, hogy mennyi időbe, fáradságba, pénzbe kerül az egyik csúcsból a másikba történő átlépés. Mi most feltesszük, hogy ezek a súlyok mind nemnegatív értékek.1 Mivel a helységek közötti autóutak kétirányúak, ezért az első probléma gráfja irányítatlan. A második problémát leíró gráf irányított, hiszen sokszor előfordul, hogy két város között csak az egyik irányba van járat, vagy van oda-vissza járat, de nem ugyanannyiba kerül.
A problémáinkat egyszerű gráfokkal tudjuk leírni, amelyek nem tartalmaznak hurokélt vagy többszörös élt. Válasszunk a gráf ábrázolásához először egy szomszédsági mátrixot. Élsúlyozott gráfoknál annyiban módosul a mátrix, hogy nem csak a két csúcs közötti kapcsolat meglétét vagy hiányát lehet kiolvasni belőle, hanem a súly értékét is. A mátrix i-edik sorának j-edik eleme az i-edik csúcsból a j-edikbe vezető él súlyát tartalmazza. Két kiegészítést kell tennünk: egyrészt az (i,i) él értéke legyen nulla (a helyben maradás nem jelent költséget), illetve ha két csúcs között nincs él, akkor a költség/távolság/idő legyen végtelen nagy.
Vegyük példaként a következő gráfot és a hozzá tartozó mátrixot: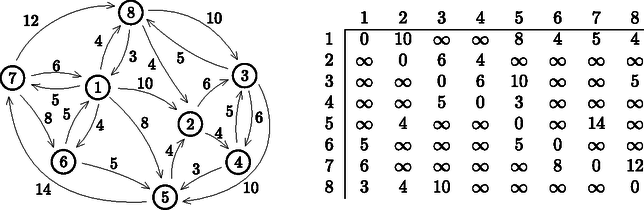

 
 

A feladatunk tehát egy legkisebb költségű útvonal meghatározása két csúcs között. Nézzük, hogy mit tudunk tenni az eddig tanultak alapján. A korábban megismert szélességi és mélységi keresés segítségével felfedeztünk egy útvonalat (amennyiben volt út) a cél csúcsig, vagy a kiinduló csúcsból elérhető részgráf bejárása után megtudtuk, hogy a cél csúcsba nem tudunk eljutni. A szélességi keresés egy legrövidebb utat adott meg a két csúcs között. Igazából most is valami hasonlóra volna szükség, csak a két csúcs közötti ,,távolságot'' nem az útvonalon érintett élek száma, hanem az élek súlyának összege határozza meg. A szélességi keresést próbáljuk meg úgy módosítani, hogy ne a Start csúcstól való távolság, hanem a Start csúcstól vett költség összege legyen meghatározó a bejárásnál.
Induljunk el a Start csúcsból, és válasszuk a legkisebb költségű élt. Ha ezzel szerencsés esetben elértük a Cél-t, akkor készen vagyunk, és biztosan a lehető legkisebb költségű utat választottuk. Ha nem értünk célba, akkor mérjük föl, hogy a Start csúcsból, valamint az előbb elért csúcsból elérhető csúcsok közül melyikhez vezet a legkisebb költségű út a Start csúcsból, és azon haladjunk tovább. Ha most elértük a Cél csúcsot, akkor a választásunk miatt az útvonal optimális költségű. Ha az elért csúcs most sem a Cél, akkor most már a három csúcsból lépünk tovább, és megint azon az élen, amelyen a Start csúcsból a legkisebb költséggel jutunk el egy eddig még el nem ért csúcshoz. Ezekkel a lépésekkel a Start csúcsból elérhető részgráf minden csúcsához eljutunk, és ha közben a Cél csúcshoz érünk, akkor azt egy legkisebb költségű úton tesszük.
Az algoritmust először Edsger Wybe Dijkstra, holland informatikus fogalmazta meg 1956-ban. Egyrészt jól látható, hogy ha a súlyokat azonos értéknek választjuk, akkor magát a szélességi keresést kapjuk. Másrészt ha nem csak egy csúcshoz, hanem a Start csúcstól az összes elérhető csúcshoz vezető legkisebb költségű utakra vagyunk kíváncsiak, akkor az algoritmus megadja azokat, ahogyan a szélességi bejárás is megadta az összes elérhető csúcshoz az egyik legrövidebb utat.
A Dijkstra-algoritmus működése során tehát elindulunk a Start csúcsból, majd fokozatosan olyan csúcsokhoz érünk el, amelyekhez az oda vezető út optimális. Az így elért csúcsok olyan részhalmazát alkotják a gráf összes csúcsának, amelynek csúcsaihoz már ismerünk egy optimális utat. Az algoritmus minden menetben kiválasztja a halmazból közvetlenül elérhető, de még azon kívüli csúcsok közül a legkisebb költséggel elérhető csúcsot. A választáshoz tudnunk kell, hogy mely csúcsok vannak a halmazban, amit legegyszerűbben most is egy logikai tömbben tárolhatunk (jártunk). Ezen kívül tudnunk kell még, hogy a halmazon kívüli csúcsok közül melyik mekkora költséggel érhető el a Start csúcstól. Ehhez fölveszünk egy d tömböt, amely minden csúcsra megadja, hogy a keresés során szerzett információk alapján az adott csúcs milyen költségű úton érhető el. Kezdetben a d tömbben a Start csúcshoz 0-t, a többi helyre ∞-t írunk. Amikor bővítjük egy csúccsal a halmazt, akkor a d tömb értékeit a halmazon kívüli elemekre módosítjuk, hiszen lehetséges, hogy azokhoz az aktuális csúcson át vezet egy kisebb költségű út. Nézzük tehát az algoritmust, amely egy m mátrixszal adott, N csúcsot tartalmazó, élsúlyozott gráfban megkeresi a Start csúcsból a Cél csúcsig vezető optimális utat.

Dijkstra-algoritmus (m, N, Start, Cél)
    d[] := ∞
    jártunk[] := hamis
    d[Start] := 0
    Ciklus
        min := ∞
        Ciklus cs := 1-től N-ig
            Ha nem jártunk[cs] és d[cs]<min akkor
                min := d[cs]
                csúcs := cs
            Elágazás vége
        Ciklus vége
        Ha min<∞ akkor
            jártunk[csúcs] := igaz
            Ciklus cs := 1-től N-ig
            Ha nem jártunk[cs] és d[cs]>d[csúcs]+m[csúcs][cs] akkor
                     d[cs] := d[cs]+m[csúcs][cs]
            Elágazás vége
        Ciklus vége
    Ciklus vége ha min=∞ vagy csúcs=Cél
Dijkstra-algoritmus vége
 
Az algoritmus eredményét a d táblázatban találjuk. A táblázat Cél csúcsnak megfelelő értéke adja az oda vezető legrövidebb út hosszát, vagyis a keresett legkisebb értéket. Amennyiben nincs út, akkor az érték végtelen marad.
Érdemes még egyszer átgondolni, hogy a Dijkstra-algoritmus a szélességi keresés egy módosított változata, és meglátni a közöttük lévő hasonlóságokat és különbségeket. Ebben segítenek a következő kérdések és feladatok:
1. Adjuk meg pontosan, hogy a Dijkstra-algoritmus fenti változatában mit tartalmaznak az algoritmus lefutása után a d tömb elemei?
2. Hogyan kellene módosítani az algoritmust, hogy a Cél csúcshoz vezető utat is megkapjuk?
3. Hogyan változtassuk meg az algoritmust, ha minden a Start csúcstól elérhető csúcsra szeretnénk megismerni az oda vezető optimális út hosszát?
4. Hogyan valósítja meg a szélességi keresés Sor-át a Dijkstra-algoritmust?
5. Adjunk becslést a 3. feladat szerint módosított algoritmus lépésszámára N függvényében.
1A feladatok egy részénél természetesen előfordulhatnak negatív értékek, pl. egy domborzati térképen a a fölfelé mozgás pozitív, míg a lefelé mozgás negatív súlyt jelent, vagy egy játék különböző helyzetei között a játékosok nyernek vagy veszítenek pontokat.