Cím:	Megoldásvázlatok a 2016/3. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	A Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium matematika munkaközössége
Füzet:	2016/április, 202 - 209. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. $A=\left\{\mathrm{1,2,3,4}\right\}$, $B=\left\{\mathrm{1,2,3,4,5,6,7,8}\right\}$. $a)$ Hány $f:A\to B$ függvény létezik? $b)$ Ezek közül hány olyan van, amely szigorúan monoton növő? $c)$ Az $a)$ pontban tekintett összes függvény között hány olyan van, amelynek értékkészlete pontosan három elemet tartalmaz?  (12 pont)   Megoldás. $a)$ Az $A$ halmaz minden eleméhez a $B$ halmaz bármelyik elemét rendelhetem, azaz nyolc elem közül választhatok. Mivel az $A$ halmazban négy elem van, a függvények száma: $8^4=4096$. $b)$ Ilyenkor az értékkészlet négy elemű. A $B$ halmazból tetszőlegesen választott négy elem esetén a szigorúan monoton növő függvény egyértelműen meghatározott. A keresett függvények száma tehát: $\left(\genfrac{}{}{0ex}{}{8}{4}\right)=70$. $c)$ Ha az értékkészlet három elemű, akkor az $A$ halmaz két eleméhez ugyanazt rendeljük, a másik kettőnek az értéke viszont ettől és egymástól is különböző. Kiválasztjuk $A$ azon két elemét, melyek értéke azonos lesz, ezt $\left(\genfrac{}{}{0ex}{}{4}{2}\right)=6$ féleképpen lehet megtenni, hozzájuk a $B$ halmazból nyolc féle elemet rendelhetünk. Az $A$ halmazból a maradék két elem közül a kisebbhez hét, a nagyobbhoz hat féle számot rendelhetünk a $B$ halmazból. Tehát a keresett függvények száma: $\left(\genfrac{}{}{0ex}{}{4}{2}\right)\cdot 8\cdot 7\cdot 6=2016$.   2. $a)$ Osszuk fel az $1$-et négy nemnegatív részre úgy, hogy a részek számtani sorozatot alkossanak. Milyen nagy lehet a sorozat differenciája? $b)$ Osszuk fel az $1$-et négy részre úgy, hogy a részek $2$ hányadosú mértani sorozatot alkossanak. Mennyi a sorozat első eleme? $c)$ Osszuk fel az $1$-et négy részre úgy, hogy a részek mértani sorozatot alkossanak. Milyen nagy lehet a sorozat hányadosa?  (12 pont)   Megoldás. $a)$ Jelölje a számtani sorozat első elemét $a$, a differenciát $d$. Ekkor $a\ge 0$. A feltétel szerint $1=4a+\frac{1}{2}\cdot 4\cdot 3d$, azaz $1\ge 6d$, tehát $\frac{1}{6}\ge d$ és $a=\frac{1}{4}-\frac{3}{2}d$. A $d=\frac{1}{6}$ eset is lehetséges, ekkor $a=0$. $b)$ Legyen a sorozat első eleme $g$. Ekkor $1=g\left(2^4-1\right)=15g$, azaz $g=\frac{1}{15}$. $c)$ Jelölje az első elemet $g$, a hányadost pedig $q$. Most $q>0$, így $g>0$. A feltétel szerint $1=g\frac{q^4-1}{q-1}$, ahonnan $\frac{1}{g}=q^3+q^2+q+1<4q^3$, ha $q>1$. Mivel $g$-ről csak annyit kötöttünk ki, hogy pozitív, $\frac{1}{g}$ akármilyen nagy lehet. Innen pedig következik, hogy a mértani sorozat hányadosa is akármilyen nagy lehet. 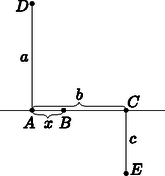  3. Adjuk meg az $f\left(x\right)=x+\sqrt[]{x^2-4}$ függvény értelmezési tartományát és értékkészletét.  (13 pont)   Megoldás. A függvény értelmezési tartománya a $-2$-nél nem nagyobb, illetve a $2$-nél nem kisebb számok. Vizsgáljuk meg, hogy az $y=x+\sqrt[]{x^2-4}$ paraméteres egyenletnek milyen $y$-ra van megoldása. Rendezve: $y-x=\sqrt[]{x^2-4}$. Az $x^2\ge 4$ feltételt teljesítő számok adják a jobb oldal értelmezési tartományát, és csak olyan $x$ értékek adhatnak megoldást, melyekre $y\ge x$. Elvégezve a négyzetre emelést, rendezés után az $y^2+4=2yx$ egyenletre jutunk. Ennek (és az eredetinek) $y=0$ esetén nincs megoldása, tehát $x=\frac{y^2+4}{2y}$. Figyelembe véve az $y\ge x$ feltételt, $0\ge \frac{4-y^2}{2y}$. Ennek megoldása: $-2\le y<0$ vagy $2\le y$. Ezekhez az $y$ értékekhez tartozó $x$-ek megoldásai a feladatnak, így megkaptuk az értékkészletet.   4. Keressük meg az alábbi függvény minimumhelyét: $\begin{array}{c}{\displaystyle f\left(x\right)=\sqrt[]{a^2+x^2}+\sqrt[]{{\left(b-x\right)}^2+c^2}\mathrm{,}\text{<span style="font-style: italic;">ahol</span>}a\mathrm{,}b\mathrm{,}c\mathrm{,}x\in {\text{R}}^{+}\mathrm{.}}\end{array}$  (14 pont)   Megoldás. A feladat szövegéből nem következik, hogy geometriai szélsőérték problémával van dolgunk, de a ,,Pithagorasz-tétel gyanús'' kifejezések látványa, és a feladatban szereplő pozitív paraméterek orientálják a megoldást.     Vegyük fel az $AC=b$ hosszúságú szakaszt, annak végpontjaiban, $AC$-re merőlegesen, az $AC$ egyenes különböző partján az $AD=a$ és a $CE=c$ hosszúságú szakaszokat. $B$ pont végigfut az $AC$ félegyenesen. Legyen $AB=x$. Ekkor $f\left(x\right)$ éppen az $ADB$ és a $BCE$ derékszögű háromszögek átfogóinak összege. E két szakasz összege pedig (a háromszög egyenlőtlenség miatt) $B$ minden helyzetében nagyobb, vagy egyenlő, mint a $DE$ szakasz. Egyenlőség akkor és csak akkor van, ha a $B$ pont éppen az $AC$ és a $DE$ egyenesek metszéspontja. Tehát ekkor minimális a függvényérték. Ezután az $ADB$ és $BCE$ derékszögű háromszögek hasonlóságából kiszámítható $x$ értéke: $a:x=c:\left(b-x\right)$, ahonnan $x=\frac{ab}{a+c}$.   II. rész     5. Adjunk meg $13$ darab pozitív egész számot úgy, hogy a mediánjuk $2$, az átlaguk $2000$ legyen. Létezik-e ilyen sokaság, ha azt is megköveteljük, hogy egyetlen módusza legyen, aminek értéke $a)$ $1;$ $b)$ $2;$ $c)$ $1514;$ $d)$ $6000?$ $e)$ Mennyi lehet maximum a módusz?  (14 pont)   Megoldás. A feltételek szerint a nagyság szerint rendezett minta hetedik eleme $2$, az elemek összege $13\cdot 2000=26000$. $a)$ Ha az egyetlen módusz az $1$, akkor például kielégíti a feltételeket a következő számsorozat: 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 12 992; 12 992. $b)$ Ha az egyetlen módusz a $2$, akkor például kielégíti a feltételeket a következő számsorozat: 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 2; 25 976. $c)$ Ha az egyetlen módusz az $1514$, akkor például kielégíti a feltételeket a következő számsorozat: 1; 1; 1; 1; 2; 2; 2; 1514; 1514; 1514; 1514; 1514; 18 420. $d)$ A számok között az 1-es és a 2-es közül legalább az egyikből négy darab van. Ha az egyetlen módusz a $6000$, akkor abból legalább ötnek kell lennie, de akkor a számok összege már több, mint 26 000, ami ellentmondás. $e)$ Nem lehet a számok között hat darab $1$-es, mert akkor a keresett szám nem az egyetlen módusz. Öt darab $1$-es mellé hat egyforma elem kell, és ennek maximuma biztos kisebb, mint ha csak öt nagy szám kell, és az egyik 1-est 2-esre cseréljük. Ebből következik, hogy az első hét szám összege legalább $4\cdot 1+3\cdot 2=10$. Nézzük meg, hogy ezt 26 000-ből kivonva, mi a legnagyobb szám, ami még ötször választható. Ez az 5198. Ekkor azonban a 13. értéknek $0$-nak kellene lennie, ami lehetetlen. A maximális módusz tehát az 5197, ami jó is. Pl.: 1; 1; 1; 1; 2; 2; 2; 5; 5197; 5197; 5197; 5197; 5197. 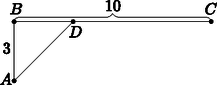  6. Egy gyalogos a hóval borított mező $A$ pontjában van, $3$ kilométernyire a $BC$ egyenes úttól $($az ábrán $AB=3$ km, $BC=10$ km).     Az országúton a gyalogos kétszer akkora sebességgel halad, mint a hómezőn. Mely $D$ pontban kell kimennie a gyalogosnak az útra, hogy a legrövidebb idő alatt jusson $C$-be?  (16 pont)   Első megoldás (paraméterezés). Legyen $BD=x$, ekkor $DC=10-x$, $AD=\sqrt[]{x^2+9}$. Ha a gyalogos sebessége a hómezőn $v$, az országúton $2v$, akkor az $ADC$ utat $t=\frac{\sqrt[]{x^2+9}}{v}+\frac{10-x}{2v}$ idő alatt teszi meg. Megkeressük azon $t$ értékeket, amelyekre a $t=\frac{\sqrt[]{x^2+9}}{v}+\frac{10-x}{2v}$ egyenletnek van megoldása. (Azt is láthatjuk, hogy a szélsőértékhely meghatározásakor pl. egységnyinek választhatjuk a $v$ sebességet.) Rendezzük át az egyenletet, emeljük négyzetre és vizsgáljuk meg az így kapott másodfokú paraméteres egyenletet: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 2\sqrt[]{x^2+9}}& {\displaystyle =2t+x-\mathrm{10,}}\hfill \\ \hfill {\displaystyle 4x^2+36}& {\displaystyle =4t^2+x^2+100-40t+4tx-20x\mathrm{,}}\hfill \\ \hfill {\displaystyle 3x^2+4x\left(5-t\right)-4\left(t^2-10t+16\right)}& {\displaystyle =0.}\hfill \end{array}}$ Világos, hogy ennek az egyenletnek akkor lehet megoldása, ha diszkriminánsa nemnegatív: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle D=16{\left(5-t\right)}^2-4\cdot 3\cdot \left(-4\right)\cdot \left(t^2-10t+16\right)}& {\displaystyle \ge \mathrm{0,}}\hfill \\ \hfill {\displaystyle 4t^2-40t+73}& {\displaystyle \ge \mathrm{0,}}\hfill \\ \hfill {\displaystyle 4\left(t-5-\frac{3}{2}\sqrt[]{3}\right)\left(t-5+\frac{3}{2}\sqrt[]{3}\right)}& {\displaystyle \ge \mathrm{0,}}\hfill \end{array}}$ s ekkor $t\le 5-\frac{3}{2}\sqrt[]{3}$ vagy $t\ge 5+\frac{3}{2}\sqrt[]{3}$. $AC=\sqrt[]{{10}^2+9}\approx 10\mathrm{,}44$. Ha ezt az utat az ,,országúti'' sebességgel tenné meg a gyalogos, akkor is $\frac{10\mathrm{,}44}{2}=5\mathrm{,}22$ egységnyi időre lenne szüksége; vagyis a $t\le 5-\frac{3}{2}\sqrt[]{3}$ lehetőséget kizárhatjuk. Kaptuk: $t\ge 5+\frac{3}{2}\sqrt[]{3}$, vagyis ha a gyalogos sebessége $v$, akkor legkevesebb $\begin{array}{c}{\displaystyle \frac{5+\frac{3}{2}\sqrt[]{3}}{v}}\end{array}$ egységnyi idő alatt tudja megtenni az $ADC$ utat. Ha a $3x^2+4x\left(5-t\right)-4\left(t^2-10t+16\right)=0$ egyenlet diszkriminánsa $0$, akkor $\begin{array}{c}{\displaystyle x=\frac{4\left(t-5\right)}{2\cdot 3}=\sqrt[]{3}\mathrm{.}}\end{array}$   Második megoldás (elemi geometria). Átfogalmazzuk a feladatot: ha a gyalogos sebessége a hómezőn egységnyi, akkor a $BC$ egyenesen olyan $D$ pontot keresünk, amelyre $AD+\frac{DC}{2}$ minimális. Vegyük fel a $BC$ egyenes által meghatározott, $A$-t nem tartalmazó félsíkjában a $C$-ből kiinduló $e$ félegyenest úgy, hogy $BC$-vel bezárt szöge ${30}^{\circ }$ legyen, majd bocsássunk $D$-ből merőlegest erre az egyenesre (a talppontot jelöljük $E$-ve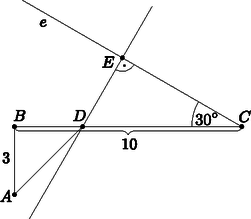l).     Ekkor $DE=\frac{DC}{2}$ (hiszen az $EDC$ derékszögű háromszög egy szabályos háromszög fele), s tetszőleges $D$ pont esetén az $AD+DE$ összeget kell minimalizálnunk, ahol $DE$ merőleges $e$-re. $AD+DE$ akkor lesz a lehető legkisebb, ha ez a három pont egy egyenesbe esik, vagyis ha $ADB\sphericalangle ={60}^{\circ }$. Ez az eredmény természetesen ugyanaz, mint az előző megoldásban kapott érték, hiszen $\begin{array}{c}{\displaystyle \sqrt[]{3}=\text{tg}{60}^{\circ }=\frac{AB}{BD}=\frac{3}{\sqrt[]{3}}\mathrm{.}}\end{array}$   Harmadik megoldás (fizikai szemlélet). Képzeljük el, hogy az $A$ pontba egy fényforrást helyezünk, ahonnan a fény a két közeg határvonalán lévő $C$ pontba jut. Mivel a fény két pont között mindig a minimális ideig tartó úton halad, nekünk a feladatban éppen azt a $D$ pontot kell meghatároznunk, amely mellett a fénysugár beesési szöge a határszöggel egyezik meg, azaz a törési szög ${90}^{\circ }$.     A geometriai optika Snellius‐Descartes-törvénye szerint $\begin{array}{c}{\displaystyle \frac{\text{sin}\alpha }{\text{sin}\beta }=\frac{v_1}{v_2}\mathrm{,}}\end{array}$ ahol $\alpha$ és $\beta$ a beesési és törési szög, $v_1$ és $v_2$ a fény sebessége a két közegben. Ebben az esetben a $BAD$ szög megegyezik a beesési szöggel (váltószögek), tehát $\begin{array}{c}{\displaystyle \frac{\text{sin}BAD\sphericalangle }{\text{sin}{90}^{\circ }}=\frac{v}{2v}\mathrm{.}}\end{array}$ Innen már megkapjuk a $BAD\sphericalangle ={30}^{\circ }$-os eredményt.   Negyedik megoldás (deriválás). A $t=\sqrt[]{x^2+9}+\frac{10-x}{2}$ függvény deriváltja $\begin{array}{c}{\displaystyle t\text{'}=\frac{1}{2\sqrt[]{x^2+9}}\cdot 2x-\frac{1}{2}\mathrm{,}}\end{array}$ ennek zérushelye: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \frac{1}{2\sqrt[]{x^2+9}}\cdot 2x-\frac{1}{2}}& {\displaystyle =\mathrm{0,}}\hfill \\ \hfill {\displaystyle \sqrt[]{x^2+9}}& {\displaystyle =2x\mathrm{,}}\hfill \end{array}}$ s mivel $x>0$, azért $x^2+9=4x^2$, amiből $x=\sqrt[]{3}$. Ha $x<\sqrt[]{3}$, akkor $t\text{'}<0$; ha $x>\sqrt[]{3}$, akkor $t\text{'}>0$. Ezért $t$-nek az $x=\sqrt[]{3}$ helyen minimuma van.   7. Egy társaságban öt ember találkozott, jelölje őket $A$, $B$, $C$, $D$, $E$. Köztük az ismeretségek kölcsönösek. Megkérdeztük őket, kinek hány ismerőse van ötük között. $A$ azt mondta, négy embert ismer. $C$-ről kiderült, hogy ugyanannyi ismerőse van, mint $D$-nek. $D$ azt mondta, hogy eggyel kevesebb ismerőse van, mint $E$-nek. $E$ ismerőseinek száma páratlan. $a)$ Hány embert ismer $D$? $b)$ Ismerheti-e egymást $B$ és $D$? $c)$ Ismerheti-e egymást $C$ és $D$?  (16 pont)   Megoldás. Mivel $A$ négy embert ismer, ő mindenkit ismer. Ez azt is jelenti, hogy mindenki más legalább egy embert ismer, hiszen $A$-t ismerik. Ezek szerint $D$ is legalább egy embert ismer. $E$ több embert ismer, mint $D$ és páratlan sokat, tehát hármat ismer. Ebből kiderül, hogy $D$ is és $C$ is 2 embert ismer. Az ismerősök számáról tehát a következőket tudjuk: $A$-nak 4, $B$-nek $b$, $C$-nek 2, $D$-nek 2, $E$-nek 3. Most megmutatjuk, hogy $B$-nek 1 vagy 3 ismerőse lehet. Szemléltessük az ismeretségeket egy rajzon; az embereket jelölje egy-egy pont, és ha ismerik egymást, kössük össze őket. Az összekötő vonalak végpontjainak száma a vonalak számának kétszerese. Ez éppen az egyes emberek ismerősei számának összege. (A gráfok nyelvén: az élek számának kétszerese a fokszámok összege.) Ez utóbbi $4+b+2+2+3=\text{(a}$ vonalak számának kétszerese). Ezek szerint $b$ páratlan, tehát 1 vagy 3 lehet. Az ismeretségeket szemléltető gráfok a következők lehetnek:     A 3. ábra mutatja, hogy $B$ és $D$ ismerheti egymást. Ha $C$ és $D$ ismerné egymást, akkor nekik már nem lehetne további ismerősük, így $E$ csak $A$-t és $B$-t ismerhetné és nem lenne 3 ismerőse. Tehát $C$ és $D$ nem ismerik egymást.   8. Jelölje $k$ az $x^2+y^2-25x-48y+576=0$ egyenletű kört. Határozzuk meg $k$ minden olyan érintő egyenesének egyenletét, amelyre teljesül, hogy az $y$ tengely és a $k$ kör közé eső szakaszának hossza $9\mathrm{,}375$ egység.  (16 pont)   I. megoldás (a szerkesztést követve). Keressük meg ezen érintők $y$ tengellyel vett metszéspontját. Határozzuk meg először azon pontok mértani helyét, amelyekből a $k$ körhöz húzott érintő hossza 9,375 egység. Ennek a mértani helynek az $y$ tengellyel való metszéspontjai lesznek a keresett pontok.     A vizsgált mértani hely egy $k$-val koncentrikus $k_e$ kör. Valóban, ha a $P$ pontból az $U$ középpontú $k$ körhöz húzott $PT$ érintőszakasz hossza rögzített, $PU$ értéke is állandó, hiszen az $UTP$ derékszögű háromszögben $P{U}^2=P{T}^2+T{U}^2$. Esetünkben $k$ egyenlete ${\left(x-12\mathrm{,}5\right)}^2+{\left(y-24\right)}^2=12\mathrm{,}{5}^2$ alakba írható át, azaz $U\left(12\mathrm{,}5;24\right)$, $r=TU=12\mathrm{,}5$, így a $P\left(x\mathrm{,}y\right)$ pontból $k$-hoz húzott érintő hossza pontosan akkor 9,375 egység, ha $\begin{array}{c}{\displaystyle k_e:{\left(x-12\mathrm{,}5\right)}^2+{\left(y-24\right)}^2=9\mathrm{,}{375}^2+12\mathrm{,}{5}^2\mathrm{.}}\end{array}$ Az $y$ tengely pontjait az $x=0$ feltétel jellemzi, tehát a keresett pontok $y$ koordinátáira $\begin{array}{c}{\displaystyle {\left(0-12\mathrm{,}5\right)}^2+{\left(y-24\right)}^2=9\mathrm{,}{375}^2+12\mathrm{,}{5}^2\mathrm{,}\text{amiből}y=24\pm 9\mathrm{,}\mathrm{375,}}\end{array}$ azaz $P_1\left(0;\mathrm{33,375}\right)$, $P_2\left(0;\mathrm{14,625}\right)$. Ekkor a $P_1$ ponton átmenő érintő egyenlete $\begin{array}{c}{\displaystyle y=mx+\left(24+9\mathrm{,}375\right)=mx+24+\frac{75}{8}\mathrm{.}}\end{array}$ Ezt behelyettesítve a $k$ kör egyenletébe: $\begin{array}{c}{\displaystyle x^2+{\left(mx+24+\frac{75}{8}\right)}^2-25x-48\left(mx+24+\frac{75}{8}\right)+576=0.}\end{array}$ Rendezve: $\begin{array}{c}{\displaystyle \left(m^2+1\right)x^2-\left(25-\frac{75}{4}m\right)x+{\left(\frac{75}{8}\right)}^2=0.}\end{array}$ Pontosan akkor lesz az egyenes érintő, ha ennek a másodfokú egyenletnek a diszkriminánsa 0: $\begin{array}{c}{\displaystyle {\left(25-\frac{75}{4}m\right)}^2-4\left(m^2+1\right){\left(\frac{75}{8}\right)}^2=\mathrm{0,}\text{amiből}-25\cdot \frac{75}{2}m=4\cdot \frac{{75}^2}{8^2}-{25}^2\mathrm{,}}\end{array}$ vagyis $m=\frac{7}{24}$. Az egyenlet: $y=\frac{7}{24}x+24+\frac{75}{8}$. A $P_2$-n átmenő érintő ennek az $y=24$ egyenesre vonatkozó tükörképe, tehát meredeksége $-\frac{7}{24}$, egyenlete pedig 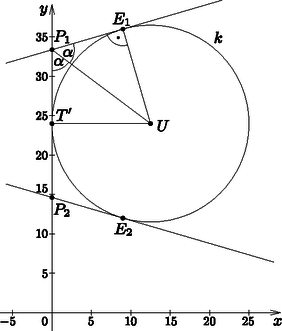$y=-\frac{7}{24}x+24-\frac{75}{8}$.   II. megoldás (ad hoc). Vegyük észre, hogy a $k$ kör egyenlete $\begin{array}{c}{\displaystyle {\left(x-12\mathrm{,}5\right)}^2+{\left(y-24\right)}^2=12\mathrm{,}{5}^2\mathrm{,}}\end{array}$ vagyis a kör a $T\text{'}\left(0;24\right)$ pontban érinti az $y$ tengelyt.     Az $y$ tengely tetszőleges $P$ pontjából a $k$ körhöz húzott $P\text{'}T$ érintő hossza az érintő szakaszok egyenlősége révén $PT\text{'}$-vel egyenlő, azaz a keresett pontok: $\begin{array}{c}{\displaystyle P_{\mathrm{1,2}}\left(0;24\pm 9\mathrm{,}375\right)\mathrm{.}}\end{array}$ Mivel $9\mathrm{,}375<12\mathrm{,}5$, ezért a $P_1$ pontból húzott érintő meredeksége pozitív, a $P_2$ pontból húzotté pedig negatív. Legyen $T\text{'}{P}_{1}U\sphericalangle =\alpha$, ekkor $E_1{P}_{1}U\sphericalangle =\alpha$ és $T\text{'}{P}_1{E}_1\sphericalangle =2\alpha$, valamint $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{12\mathrm{,}5}{\frac{75}{8}}=\frac{\frac{25}{2}}{\frac{75}{8}}=\frac{4}{3}\mathrm{.}}\end{array}$ A $P_1$-ből húzott érintő $m$ meredekségére: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle m}& {\displaystyle =\text{tg}\left(2\alpha -{90}^{\circ }\right)=\text{tg}\left(\alpha +\left(\alpha -{90}^{\circ }\right)\right)=\frac{\text{tg}\alpha +\text{tg}\left(\alpha -{90}^{\circ }\right)}{1-\text{tg}\alpha \cdot \text{tg}\left(\alpha -{90}^{\circ }\right)}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\text{tg}\alpha -\frac{1}{\text{tg}\alpha }}{1+\text{tg}\alpha \cdot \frac{1}{\text{tg}\alpha }}=\frac{\frac{4}{3}-\frac{3}{4}}{2}=\frac{7}{24}\mathrm{.}}\hfill \end{array}}$ (Felhasználtuk, hogy $\text{tg}\alpha =-\text{tg}\left(-\alpha \right)$ és $\text{tg}\left({90}^{\circ }-\alpha \right)=\text{ctg}\alpha =\frac{1}{\text{tg}\alpha }$.) Tehát (a szimmetria miatt) két érintő van, amely teljesíti a feltételt: $\begin{array}{c}{\displaystyle y=\frac{7}{24}x+24+\frac{75}{8}\text{és}y=-\frac{7}{24}x+24-\frac{75}{8}\mathrm{.}}\end{array}$   9. Három egymás utáni pozitív egész szám szorzatának prímtényezős felbontásában csak két különböző prímszám szerepel (tehát a szorzat $p^n{q}^m$ alakú, ahol $p$ és $q$ prímszám, $n$, $m$ pozitív egészek). Adjuk meg az összes ilyen számhármast.  (16 pont)   I. megoldás. A középső szám nagyobb 1-nél, tehát felbontásában szerepel legalább egy prímtényező. A középső szám mindkét szomszédjához relatív prím, ezért a benne szereplő prímtényező a másik két számban nem szerepelhet, e két számban tehát összesen csak egy prímtényező szerepelhet. Viszont e két számnak csak a $2$ lehet közös osztója, mert különbségük $2$. Ez kétféleképp lehetséges: vagy az első szám $1$, vagy mindkét szám 2-hatvány. Az első esetben az 1, 2, 3 számokat kapjuk. A második esetben két 2-hatvány különbsége 2, ez csak úgy lehet, ha a két szám a $2$ és a $4$, így a 2, 3, 4 számokat kapjuk. A feladat feltételének két számhármas felel meg: 1, 2, 3 és 2, 3, 4.   II. megoldás. Két szomszédos szám között van egy páros, tehát a három szám szorzata páros. Így az egyik prím a $2$, a másik egy páratlan prím. Legyen ez $p$. Ha a középső szám páros, akkor a két szélső páratlan. Nem lehet mindkettő osztható $p$-vel, mert $p$ nagyobb kettőnél. Tehát az egyik szám az 1, és mivel csak az első szám lehet 1, azért a három szám az 1, 2, 3. Ha a középső szám páratlan, akkor a két szélső páros, és mindkettő relatív prím a középsőhöz, ezért egyik sem osztható $p$-vel. De akkor mindkettő kettőhatvány. A kettőhatványok sorában: 1, 2, 4, 8, $\text{...}$ . Csak egy esetben 2 a különbség két (nem feltétlenül szomszédos) szám között: a $2$ és a $4$ esetében. Tehát a három szám a 2, 3, 4. A feladatnak tehát két számhármas tesz eleget: 1, 2, 3 és 2, 3, 4.