Cím:	Síkidomok csókszáma
Szerző(k):	Lángi Zsolt
Füzet:	2016/április, 194 - 200. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   1. Bevezetés Bár a konvex geometriának, a geometriának a konvex testekkel és síkidomokkal foglalkozó ágának gyökerei Euklidészhez és Arkhimédészhez nyúlnak vissza, a konvex testek szisztematikus vizsgálata a 20. század elején kezdődött Hermann Brunn és Hermann Minkowski munkásságával. Azóta ez a tudományág nagy jelentőségre tett szert, és a természettudományok számos ágában alkalmazásra került. A cikk célja ezen relatíve fiatal tudományterület egy ismert problémájának bemutatása. Ehhez először definiáljuk a szükséges alapfogalmakat.   1. definíció. A $K$ síkbeli halmazt konvex síkidomnak vagy konvex lemeznek nevezzük, ha (1) $K$ bármely két pontját összekötő szakasz is $K$-hoz tartozik (minden pontjából belátjuk az egész alakzatot); (2) $K$ korlátos (belerakható pl. egy nagy körbe); (3) $K$ határa, mely egy zárt, folytonos, önmagát nem metsző görbe, is $K$-hoz tartozik.     Hasonlóan lehet definiálni a konvex test fogalmát is, magasabb dimenzióban. A fenti fogalom gyengébb változataira is szükségünk lesz. Amennyiben az (1)-es tulajdonság helyett azt követeljük meg, hogy $K$-nak van olyan pontja, melyet $K$ bármely másik pontjával összekötő szakasz $K$-hoz tartozik, azt mondjuk, hogy $K$ egy csillagszerű tartomány. Ezt úgy fogalmazhatjuk meg, hogy $K$-nak legalább egy pontjából belátni $K$-t. Ha elhagyjuk az (1)-es, de megtartjuk a másik két tulajdonságot, azt mondjuk, $K$ egy topologikus lemez, vagy egyszerűen lemez vagy síkidom. Minden lemezre, így csillagszerű vagy konvex lemezre is érvényes az alábbi észrevétel.   1. megjegyzés. Legyen $S$ egy lemez. Ekkor minden egyenesnek pontosan két eltoltja van, ami $S$-et érinti.   Szükségünk lesz még az alábbi fogalomra.   2. definíció. Az $A$ és $B$ síkbeli halmazok vektorösszege vagy Minkowski-összege azon $A+B$ halmaz, melynek elemei az összes $\overrightarrow{a}+\overrightarrow{b}$ alakban felírható helyvektorú pontok halmaza, ahol $\overrightarrow{a}$ egy $A$-beli, és $\overrightarrow{b}$ egy $B$-beli pont helyvektora. Ha $\lambda \in \text{R}$, akkor a $\lambda A$ halmaz azon pontok összessége, melyek helyvektorai felírhatók $\lambda \overrightarrow{a}$ alakban, ahol $\overrightarrow{a}$ egy $A$-beli pont helyvektora.   Pongyolán fogalmazva, ha azonosnak tekintenénk a pontokat és a helyvektoraikat, akkor $A+B$ az összes $A$-beli pont és az összes $B$-beli pont összege, minden lehetséges párosításban. Így pl. két szakasz vektorösszege egy velük párhuzamos szakasz, ha párhuzamosak, ellenkező esetben pedig egy parallelogramma.   3. definíció. A $K$ konvex síkidom centrálszimmetrizáltjának az $\begin{array}{c}{\displaystyle \frac{1}{2}\left(K+\left(-K\right)\right)=\frac{1}{2}\left(K-K\right)}\end{array}$ halmazt nevezzük.   Könnyen látható, hogy minden konvex síkidom centrálszimmetrizáltja egy origóra szimmetrikus konvex síkidom.     Írásunk fő tárgya a Hugo Hadwigertől [6] származó alábbi fogalom, mely hasonlóan értelmezhető konvex testekre, illetve általában (topologikus) lemezekre. 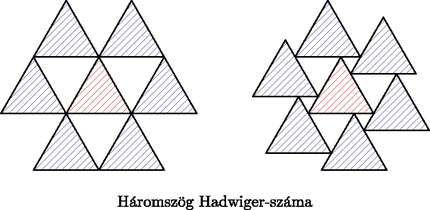  4. definíció. Egy $K$ konvex síkidom eltolt érintési száma/csókszáma/Hadwiger-száma azon eltoltjainak maximális száma, melyek az eredeti alakzatot érintik, és nincs közös belső pontjuk (nem fedik át egymást). Jele: $H\left(K\right)$.       A cikkben ismertett fő eredmény az alábbi tétel [6].   1. tétel (Hadwiger, 1957). Minden $K$ konvex síkidom Hadwiger-számára igaz az alábbi egyenlőtlenség: $6\le H\left(K\right)\le 8$.   Az előbbi példában láthattuk, hogy háromszöget hat eltoltjával tudunk érinteni. Meggondolható az is, hogy parallelogramma esetében nyolc eltoltját is köré tudjuk pakolni. A következő részben Hadwiger tételét igazoljuk.   2. Hadwiger tételének bizonyítása Legyen $K$ egy konvex síkidom, és jelölje $K$ eltoltját az $\overrightarrow{x}$ vektorral $\overrightarrow{x}+K$. Az első eszköz, amihez a bizonyításhoz szükségünk lesz, Minkowski [10] egy eredménye.   1. lemma (Minkowski, 1904). Legyen $K$ centrálszimmetrizáltja $M$. Ekkor tetszőleges $\overrightarrow{x}$ és $\overrightarrow{y}$ vektorokra $\overrightarrow{x}+K$ és $\overrightarrow{y}+K$ pontosan akkor fednek át/érintik egymást/nincs közös pontjuk, ha $\overrightarrow{x}+M$ és $\overrightarrow{y}+M$ átfednek/érintik egymást/nincs közös pontjuk.   Bizonyítás. Először belátjuk, hogy $\overrightarrow{x}+K$ és $\overrightarrow{y}+K$ pontosan akkor metszi egymást, ha $\overrightarrow{x}+M$ és $\overrightarrow{y}+M$ is. Vegyük észre, hogy az alábbi tulajdonságok ekvivalensek. $•$ $\left(\overrightarrow{x}+M\right)\cap \left(\overrightarrow{y}+M\right)\ne \varnothing$. $•$ Léteznek $P_x\text{'}\mathrm{,}{P}_y\text{'}\mathrm{,}{P}_x\text{'}\text{'}\mathrm{,}{P}_y\text{'}\text{'}\in K$ pontok, melyek helyvektoraira $\begin{array}{c}{\displaystyle \overrightarrow{x}+\frac{1}{2}\left({\overrightarrow{p}}_x\text{'}-{\overrightarrow{p}}_x\text{'}\text{'}\right)=\overrightarrow{y}+\frac{1}{2}\left({\overrightarrow{p}}_y\text{'}-{\overrightarrow{p}}_y\text{'}\text{'}\right)\mathrm{.}}\end{array}$ $•$ Léteznek $P_x\text{'}\mathrm{,}{P}_y\text{'}\mathrm{,}{P}_x\text{'}\text{'}\mathrm{,}{P}_y\text{'}\text{'}\in K$ pontok, melyek helyvektoraira $\begin{array}{c}{\displaystyle \overrightarrow{x}+\frac{1}{2}\left({\overrightarrow{p}}_x\text{'}+{\overrightarrow{p}}_y\text{'}\text{'}\right)=\overrightarrow{y}+\frac{1}{2}\left({\overrightarrow{p}}_y\text{'}+{\overrightarrow{p}}_x\text{'}\text{'}\right)\mathrm{.}}\end{array}$ * léteznek $P_x\mathrm{,}{P}_y\in K$ pontok, melyekre $\overrightarrow{x}+{\overrightarrow{p}}_x=\overrightarrow{y}+{\overrightarrow{p}}_y$. $•$ $\left(\overrightarrow{x}+K\right)\cap \left(\overrightarrow{y}+K\right)\ne \varnothing$. Hasonló ekvivalencia igazolható, ha a $K$ és $M$ halmazok helyett $K$ és $M$ belsejét írunk. Ebből az állítás viszont már következik.  $\square$   Vegyük észre, hogy a lemma alapján tetszőleges $K$ konvex síkidom és $M$ centrálszimmetrizáltjának Hadwiger-száma egyenlő. Így Hadwiger tételét elég középpontosan szimmetrikus konvex síkidomokra igazolni. Az egyszerűség kedvéért feltesszük, hogy $K$ középpontja az $O$ origó.   Első állítás: $H\left(K\right)\le 8$. Legyen $K\text{'}$ a $K$ olyan eltoltja, amely érinti $K$-t; jelölje a középpontját $X$. Legyen $Y$ az $OX$ szakasz felezőpontja. Belátjuk, hogy $Y$ közös pontja $K$-nak és $K\text{'}$-nek. Mivel $K$ és $K\text{'}$ érintik egymást, van egy közös $P$ pontjuk. De $K$ szimmetrikus $O$-ra, így $K$ és $K\text{'}$ helyet cserél, ha $Y$-ra tükrözzük őket. Tehát $P$-nek az $Y$-ra vett $P\text{'}$ tükörképe is közös pont. De $K$ és $K\text{'}$ konvex, így a $PP\text{'}$ szakasz minden pontja közös pont, azaz $Y$ is. Hosszabbítsuk meg most az $OX$ szakaszt $X$ irányában, míg metszi $K\text{'}$ határát, és jelöljük a kapott metszéspontot $Z$-vel. Minthogy $K\text{'}$ szimmetrikus $X$-re, $\overline{OY}=\overline{YX}=\overline{XZ}=\frac{1}{3}\overline{OZ}$. Jelölje $K\text{'}$-nek a $Z$-ből háromszorosára nagyított képét $\overline{K}$. Mivel $K\text{'}$ konvex, $K\text{'}\subset \overline{K}$. Másrészt $\overline{K}$ középpontja $O$, így $\overline{K}$ a $K$-nak az $O$-ból háromszorosára nagyított képe. Tehát beláttuk, hogy $K$ minden $K$-t érintő eltoltja benne van $K$-nak az $O$ pontból háromszorosára nagyított képében. 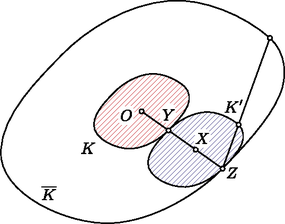    Könnyű meggondolni, hogy a nagyított kép területe $T\left(\overline{K}\right)=3^{2}T\left(K\right)=9T\left(K\right)$. Ha $K$-t $n=H\left(K\right)$ darab eltoltja érinti úgy, hogy nem fednek át, akkor $\overline{K}$ tartalmazza $K$ $\left(n+1\right)$ darab eltoltját, melyek nem fednek át. Ezek összterülete $\left(n+1\right)T\left(K\right)$. Tehát $\left(n+1\right)T\left(K\right)\le 9T\left(K\right)$, amiből $n\le 8$.   Második állítás: $H\left(K\right)\ge 6$. A bizonyításhoz az alábbi definícióra lesz szükségünk.   5. definíció. Egy középpontosan szimmetrikus hatszög affin-szabályos, ha a három, szemközti csúcsait összekötő átlója hat egybevágó háromszögre bontja.   Ennek megfelelően affin-szabályos hatszöget gyártani is tudunk: ha egy tetszőleges háromszöget tükrözünk valamelyik oldalfelező pontjára, majd folytatjuk a tükrözést úgy, hogy az eredeti háromszög valamelyik csúcsa mindegyik tükörképhez hozzátartozzon, öt tükrözés után egy affin-szabályos hatszöget kapunk. Először belátjuk, hogy $K$ tetszőleges $P$ határpontjához található olyan $K$-ba írt affin-szabályos hatszög, melynek $P$ az egyik csúcsa. Legyen $P\text{'}$ a $P$-nek az $O$-ra vett tükörképe. Ekkor $\overline{OP}=\overline{OP\text{'}}$. Toljuk el $P$ és $P\text{'}$ egyenesét valamelyik irányban párhuzamosan úgy, hogy az eltolt $K$-t egy $\frac{1}{2}\overline{PP\text{'}}$ hosszú szakaszban metszi. Ezen szakasz végpontjait $Q$-val és $R$-rel jelöljük oly módon, hogy $K$ határán körbemenve $P$, $Q$, $R$ és $P\text{'}$ ebben a sorrendben következnek. Tükrözzük a $Q$ és $R$ pontokat $O$-ra. Az így kapott, $K$ határában levő pontokat jelöljük $Q\text{'}$-vel 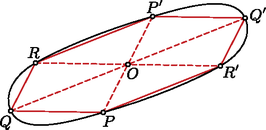és $R\text{'}$-vel.     Megmutatjuk, hogy a $PQRP\text{'}Q\text{'}R\text{'}$ hatszög affin szabályos. Valóban, a hatszög szemközti csúcsait összekötő átlók az $O$ pontban metszik egymást. Másrészt a tükrözés tulajdonságai miatt a szemközti háromszögek egybevágók. Mivel $\overline{OP}=\overline{QR}$ és $RQO\sphericalangle =QOP\sphericalangle$, így az $OQR▵$ és az $OPQ▵$ egybevágó. Hasonlóan látható be a többi háromszög egybevágósága is. Most megkonstruáljuk $K$-nak hat eltoltját, melyek nem fednek át, de $K$-t érintik. Legyen $ABCDEF$ egy $K$-ba írt affin-szabályos hatszög. Toljuk el $K$-t az $\overrightarrow{AD}$, $\overrightarrow{DA}$, $\overrightarrow{BE}$, $\overrightarrow{EB}$, $\overrightarrow{CF}$, $\overrightarrow{FC}$ vektorokkal. Belátjuk, hogy a hat eltolt érinti $K$-t és nem fednek át, melyből az igazolni kívánt egyenlőtlenség már következik. Tekintsük most $K$-t, és például az $\overrightarrow{AD}$ vektorral vett $K_D$ eltoltját. Legyen az $e$ egyenes $K$ egy érintője a $D$ pontban. Vegyük észre, hogy $D$ közös pontja $K$-nak és $K_D$-nek. Mivel a két síkidom középpontosan szimmetrikus, így őket $D$-re tükrözve a középpontjaik és ők is helyet cserélnek. Minthogy $e$ helyben marad a tükrözés során, ezért $e$ elválasztja $K$-t és $K_D$-t. De $D$ közös pontja a két síkidomnak, így $K$ és $K_D$ érintik egymást. Ugyanezzel a gondolatmenettel igazolható, hogy mind a hat eltolt érinti $K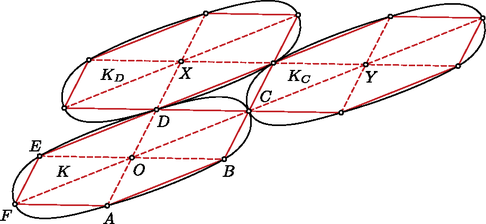$-t.     Legyen most $K$ eltoltja $\overrightarrow{FC}$-vel $K_C$. Legyen $K_D$ középpontja $X$ és $K_C$ középpontja $Y$. Könnyen látható, hogy $\overrightarrow{FC}-\overrightarrow{AD}=2\overrightarrow{OC}-2\overrightarrow{OD}=2\overrightarrow{DC}=\overrightarrow{EB}$, és $\overrightarrow{FC}-\overrightarrow{AD}=\overrightarrow{OY}-\overrightarrow{OX}=\overrightarrow{XY}$. Így $K_C$ a $K_D$ eltoltja az $\overrightarrow{XY}=\overrightarrow{EB}$ vektorral. Minthogy az előző bekezdés gondolatmenete alapján $K$ és $\overrightarrow{EB}$-vel vett eltoltja érintik egymást, így $K_C$ és $K_D$ is érinti egymást. Hasonlóan látható be, hogy minden eltolt érinti a két szomszédját. Ezzel a tételt bebizonyítottuk.  $\square$   3. További eredmények Hadwiger eredményét Branko Grünbaum [5] fejlesztette tovább az alábbi formában.   2. tétel (Grünbaum, 1961). Legyen $K$ egy konvex síkidom. (1) Ha $K$ egy parallelogramma, $H\left(K\right)=8$. (2) Ha $K$ nem parallelogramma, $H\left(K\right)=6$.   De mi a helyzet, ha $K$ nem feltétlenül konvex? Wlodzimierz és Krystyna Kuperberg, valamint Bezdek András [2] fogalmazta meg a következő kérdést, illetve sejtést.   1. kérdés (Bezdek‐Kuperberg‐Kuperberg, 1995). Igaz-e, hogy tetszőleges lemez Hadwiger-száma legfeljebb $8?$ Ha nem, van olyan szám, melyre $8$-at kicserélve igaz marad az állítás?   1. sejtés (Bezdek‐Kuperberg‐Kuperberg, 1995). Tetszőleges csillagszerű lemez Hadwiger-száma legfeljebb $8$.   A fenti kérdésre Gottfried Cheong és Mira Lee [4] adott választ 2007-ben, akik megmutatták, hogy tetszőleges $n$ pozitív egész esetén található olyan $K_n$ lemez, melyre $H\left(K_n\right)\ge n$. A sejtést érintő első eredmény Bezdek Andráshoz kötődik [1], aki 1997-ben megmutatta, hogy ha $S$ egy csillagszerű lemez, akkor $H\left(S\right)\le 75$. Lángi [8] 2009-ben igazolta, hogy ha $S$ középpontosan szimmetrikus, akkor $H\left(S\right)\le 12$. A módszerét alkalmazva született meg 2011-ben a $H\left(S\right)\le 35$ becslés tetszőleges $S$ csillagszerű lemez esetén [9]. Ezen erőfeszítések ellenére a Bezdek-Kuperberg-Kuperberg sejtés még ma is nyitott. Természetesen konvex síkidomok helyett vizsgálhatunk konvex testeket is. A síkidomok Hadwiger-számára vonatkozó felső becslés átültethető konvex testekre is. Ez alapján Hadwiger belátta, hogy minden $n$-dimenziós $K$ konvex testre $H\left(K\right)\le 3^n-1$, azaz speciálisan háromdimenziós testek esetén $H\left(K\right)\le 26$. Azt a régóta ismert alsó becslést, hogy $n$-dimenziós konvex testek Hadwiger száma legalább $n\left(n+1\right)$, Talata István [11] javította azzal 1998-ban, hogy igazolta, hogy létezik olyan $a>1$ konstans, hogy minden $n$-dimenziós $K$ konvex testre $H\left(K\right)\ge a^n$. Minthogy Minkowski lemmája alapján minden konvex test Hadwiger-száma megegyezik a centrálszimmetrizáltjának Hadwiger számával, felvetődhet bennünk, hogy igaz-e, hogy minden konvex test Hadwiger-száma páros. Ezt a kérdést, sejtés formájában, Grünbaum fogalmazta meg 1961-ben. A sejtést Talata István, majd később Joós Antal [7] cáfolta: olyan $3$-dimenziós konvex testet konstruáltak, melynek Hadwiger-száma $17$, illetve $15$. Talata István igazolta azt is, hogy minden $12$ és $26$ közti páros szám előáll, mint egy $3$-dimenziós konvex test Hadwiger-száma. Poór Attila és Talata István bizonyította, hogy ha $h\left(n\right)$ jelöli a Hadwiger-számok halmazának minimumát az $n$-dimenziós konvex testekre nézve, akkor tetszőleges $h\left(n\right)\le m\le 3^n-2$ esetén $H\left(K\right)=m$ vagy $H\left(K\right)=m+1$ alkalmas $K$ $n$-dimenziós konvex testre. Jelenleg is számos Hadwiger-számokkal kapcsolatos kérdés nyitott. Ezekről az érdeklődő olvasó Brass, Moser és Pach könyvéből [3] tájékozódhat.   Hivatkozások [1] A. Bezdek, On the Hadwiger number of a starlike disk, in: Intuitive Geometry (Budapest 1995), Bolyai Soc. Math. Studies, 6 (1997), 237‐245. [2] A. Bezdek, K. Kuperberg and W. Kuperberg, Mutually contiguous translates of a plane disk, Duke Math. J., 78 (1995), 19‐31. [3] P. Brass, W. Moser and J. Pach, Research Problems in Discrete Geometry, Springer, New York, 2005. [4] O. Cheong and M. Lee, The Hadwiger number of Jordan regions is unbounded, Discrete Comput. Geom., 37 (2007), 497‐501. [5] B. Grünbaum, On a conjecture of Hadwiger, Pacific J. Math., 11 (1961), 215‐219. [6] H. Hadwiger, Über Treffanzahlen be translationsgleichen Eikörpern, Arch. Math., 8 (1957), 212‐213. [7] A. Joós, On a convex body with odd Hadwiger number, Acta Math. Hungar., 119 (2008), 307‐321. [8] Z. Lángi, On the Hadwiger numbers of centrally symmetric starlike disks, Beiträge Algebra Geom., 50 (2009), 249‐257. [9] Z. Lángi, On the Hadwiger numbers of starlike disks, European J. Comb., 32 (2011), 1203‐1211. [10] H. Minkowski, Dichteste gitterförmige Lagerung kongruenter Körper, Nachrichten Ges. Wiss. Göttingen, Math.-Phys. Klasse (1904), 311‐355. [11] I. Talata, Exponential lower bound for the translative kissing numbers of $d$-dimensional convex bodies, Discrete Comput. Geom., 19 (1998), 447‐455.