| Cím: | Gráfalgoritmusok 5. | |
| Szerző(k): | Schmieder László | |
| Füzet: | 2016/március, 157 - 161. oldal |  PDF | MathML PDF | MathML |
| Hivatkozás(ok): | 2015/november: Gráfalgoritmusok 2.
2016/február: Gráfalgoritmusok 4. 2015/december: Gráfalgoritmusok 3. 2015/október: Gráfalgoritmusok 1. 2016/április: Gráfalgoritmusok 6. 2016/május: Gráfalgoritmusok 7. | |
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az előző részben a 2014/15. évi Informatika OKTV Döntő 3. feladatára (Családfa, elérhető pl. http://nemes.inf.elte.hu/nemes_archivum.html#2015) adtunk megoldást. Az algoritmus minden gyermektelen személytől kiindulva bejárta a szülő‐gyermek kapcsolatok által létrehozott gráfot, és megtalálta a közös ősöket. Mivel a feladatban akár 10 000 személy is szerepelhetett, ezért megpróbáltuk kiszámítani, hogy milyen nagyságrendű az algoritmus lépésszáma, nehogy nagy bemenetekre túllépjük az időkorlátot. Arra jutottunk, hogy a személyek számának négyzetével arányos lépésszámú algoritmust készítettünk. A cikk végén kértük, hogy az olvasók maguk is töprengjenek jobb megoldáson, és írják meg a KöMaL honlapján működő Fórumban az Informatika OKTV témához. Családfa2_előkészítés gysz[] := 0 szn[] := igaz gytn[] := hamis Ciklus személy := 1-től N-ig Ha él[személy][1]>0 akkor gysz[él[személy][1]] := gysz[él[személy][1]]+1 gysz[él[személy][2]] := gysz[él[személy][2]]+1 szn[személy] := hamis Elágazás vége Ciklus vége g = 0 sz = 0 Ciklus j := 1-től N-ig Ha gysz[j]=0 akkor g := g+1; ind[j] := g; gytn[j] := true különben sz := sz+1 ; ind[j] := sz Elágazás vége Ciklus vége gy[] := hamis Családfa2_előkészítés vége Az előkészítést végző algoritmus lépésszáma a három ciklusban és az méretű tömbökben -nel arányos, míg a gy tömb feltöltése ugyan -tel, de ez a lépés egy egyszerű memóriafeltöltés azonos értékkel, amit a legtöbb rendszerben hatékonyan megvalósítanak. Nézzük a bejárást, amely úgy kezdődik, hogy betesszük a sorba a gyermektelen, de ugyanakkor szülőként előforduló személyeket. Minden lépésben kiveszünk egy személyt a sorból, a gysz értékét a két szülőknél csökkentjük, és a szülők gy táblázatát a személyhez való elérhetőségekkel bővítjük. A sorba helyezünk minden olyan szülőt, aki nem ős, és az eddigiek során összegyűjtött minden információt, azaz minden hozzá vezető élt már bejártunk. A ciklus most is addig folytatódik, amíg van a sorban személy. Családfa2 él_tömb_elkészítése családfa2_előkészítés Sor_legyen_üres Ciklus csúcs := 1-től N-ig Ha gysz[csúcs]=0 és nem szn[csúcs] akkor Sorba(csúcs) Ciklus vége Ciklus amíg Sor nem üres Sorból(személy) szülő1 := él[személy][1] szülő2 := él[személy][2] gysz[szülő1] := gysz[szülő1]-1 gysz[szülő2] := gysz[szülő2]-1 Ha gytn[személy] akkor gy[(ind[szülő1]-1)*g+ind[személy]] := igaz gy[(ind[szülő2]-1)*g+ind[személy]] := igaz különben Ciklus gyk := 1-től g-ig Ha gy[(ind[személy]-1)*g+gyk] akkor gy[(ind[szülő1]-1)*g+gyk] := igaz gy[(ind[szülő2]-1)*g+gyk] := igaz Elágazás vége Ciklus vége Ha gysz[szülő1]=0 és nem szn[szülő1] akkor Sorba(szülő1) Ha gysz[szülő2]=0 és nem szn[szülő2] akkor Sorba(szülő2) Ciklus vége Családfa2 vége A bejárás után nincs más dolgunk, mint végignézni a lehetséges ősök gy táblázatát, és amelyiknél minden bejegyzés igaz, azokat megszámoljuk, és sorrendben a kimenetre írjuk. Gondoljuk végig, hogy a második megoldás valóban hatékonyabb lett-e az elsőnél. Az előkészítésről beszéltünk, most vizsgáljuk meg a bejárást. Bár összetettebb az egy csúccsal végzett feladat, mégis biztosan egyszer kerül be minden csúcs a sorba, tehát egyetlen élen sem fogunk kétszer áthaladni. Mivel a sorba számú csúcs kerül be, így most is a szorzat mutatja a műveletek számát, amit szintén csak -gyel tudunk felülről becsülni. Ennek ellenére azt várjuk, hogy a második megoldás az elsőnél hatékonyabb lesz. A futásidő minden olyan esetben nyilván kisebb, amikor sok a testvér. A futásidőt persze csak úgy kaphatjuk meg, hogy összehasonlítjuk a két algoritmus alapján készült programok futásidejét azonos, nagy számú bemenetekre. Az eredményt a diagram szemlélteti. 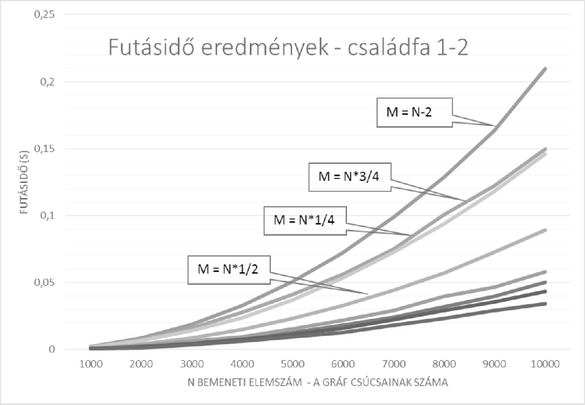 A négy nagyobb futásidőt mutató vonal a Családfa1, míg a kisebb futásidőt mutató négy vonal a Családfa2 algoritmusok alapján készült programok futásidejét mutatja. Az eredményekből egyrészt leolvasható, hogy értéke is jelentősen befolyásolja a programok futásidejét, ahogy ez természetesen várható is volt. Ugyanakkor jól látszik, hogy az algoritmusok lépésszáma a bemenet elemszámának négyzetes függvénye. Az időmérés igazolta azt a várakozásunkat, hogy a második algoritmus gyorsabb, mint az első. A feladat időkorlátjának megadott 0,5 másodperces futásidőt persze az OKTV döntőjében a programokat értékelő rendszer méri. A http://mester.inf.elte.hu oldalon elérhető az értékelést végző számítógép. Regisztráció, vagy Google azonosító segítségével használhatjuk az online programozási feladatbankot, amelyre ha feltöltjük a C/C++/Pascal vagy Java forrásprogramunkat, akkor lefordítja és futtatja azokat különböző tesztesetekre. Az értékelő rendszerben a az előző és a mostani részben közölt két algoritmus C++ változata leghosszabb futásideje 0,039 és 0,031 másodperc volt, vagyis az első programunkkal is maximális pontszámot szereztünk volna. Tapasztalatként szolgál, hogy egy legföljebb 10 000 elemszámú bemenetre kitűzött versenyfeladatra nem szükséges lépésszámú algoritmusnál hatékonyabbat készíteni. A KöMaL Fórumon is született több megoldás, amelyeket érdemes lefuttatni és megnézni. A programok közreadására és futtatására használt http://ideone.com weboldal szintén tartalmaz egy online futtató rendszert, bár értékelést nem végez, és a bemeneteket is nekünk kell megadnunk. A rendszerről más esett szó a KöMaL-ban, a 2013. decemberi I. 336. feladatban egy róla szóló útmutató elkészítése volt a cél. Feladatok és kérdések: 1. Készítsünk programot, amely a Családfa feladat egy helyes bemenetét adja, tehát a feladat leírásának megfelelő szülő‐gyermek kapcsolatrendszert tartalmaz. A program bemenete és értéke legyen. 2. Készítsük el a második algoritmus bejárásának rekurzív változatát. 3. A Fórumban a [8]-as számú bejegyzéshez tartozó program szép és rövid (szerzője a Fórumban használt nevén Róbert Gida). Próbáljuk megérteni a programot, és találjuk ki, hogy mit végez benne a fun() függvény! |