|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az előző részben a mélységi és szélességi bejárás rekurzív és nem rekurzív algoritmusait használtuk föl a Nemes Tihamér Verseny és az Informatika OKTV feladatainak megoldásához. A megoldott két példa és az önálló megoldásra javasolt harmadik feladat esetén könnyen felismerhető volt, hogy melyik gráfalgoritmust érdemes alkalmazni. A feladat pontos megértése után nem volt nehéz az eredeti algoritmusok valamelyikét módosítani. Próbáljunk most megoldani egy összetettebb, az algoritmusok közvetlen alkalmazásánál többet igénylő feladatot.
Informatika OKTV 2014/15, 11‐12. osztályosok, 3. forduló
(Családfa)
Ismerjük egy szigeten élő emberek családi leszármazotti viszonyait, a szüleiket, a szüleik szüleit, és így tovább. Minden embernek vagy mindkét szülőjét ismerjük, vagy egyiket sem. Az embereket sorszámmal azonosítjuk.
Készíts programot, amely megadja azokat az embereket, akik a gyermektelen szigetlakók mindegyikének ősei!
A standard bemenet első sorában az emberek száma () és az ismert szülőjű emberek száma (0≤M< N) van. A következő M sorban egy gyereknek és a két szülőjének sorszáma van (1≤Gyerek≠Szülő1, Gyerek≠Szülő2, Szülő1≠Szülő2≤N), egy-egy szóközzel elválasztva.
A standard kimenet első sorába a gyermektelen szigetlakók összes közös ősének számát, a második sorába pedig ezek sorszámát kell írni, növekvő sorrendben, egy-egy szóközzel elválasztva! Ha nincs közös ős, akkor az egyetlen sorba egyetlen 0-t kell kiírni!
Megjegyzés: a tesztek nem valós emberi kapcsolatokra épülnek, csupán egy feltételt vesznek figyelembe: saját magának senki sem lehet őse.
Példa:̲
Korlátok:̲
időlimit: 0,5 mp,
memórialimit: 32 MiB.
Pontozás:̲
Pontozás: a tesztek 60%-ában N< 100.
Mivel ez egy OKTV döntős feladat, ezért a megoldás értékelését számítógép végzi úgy, hogy lefuttatja a versenyző által elkészített programot bizonyos bemenetekre, és megvizsgálja a kapott kimeneteket. A korlátok most azt jelentik, hogy az összes bemeneti tesztállomány esetén legföljebb 32 MiB memóriát használhat a program, amelynek 0,5 másodpercen belül be kell fejeződnie. A feladatot futtató rendszer az esetek 60%-ában 100-nál kevesebb személyt tartalmazó bemeneti állománnyal teszteli és értékeli a programunkat, míg a többi esetben N értéke valószínűleg nagyobb 100-nál. Ha olyan programot készítünk, amely 100-nál kisebb bemenetekre lefut 0,5 másodperc alatt, akkor a feladatért kapható pontok 60%-ra biztosan számíthatunk. Ha a program a nagyobb elemszámú bemenetekre nem fut le, mert nem tud elegendő memóriát foglalni vagy nem fejeződik be időre, akkor azokra a tesztesetekre nem kapunk pontot.
Nézzük meg, hogy eddigi ismereteink alapján hogyan oldanánk meg a feladatot. A családi kapcsolatok leírására kiválóan alkalmazhatók a gráfok: a személyeket a gráf csúcsai, a szülő-gyermek viszonyt az élek reprezentálják. Matematikailag is helyes a ,,családfa'' kifejezés, mivel egy ilyen gráfban ‐ a megjegyzés ezt külön hangsúlyozza ‐ nem fordulhat elő irányított kör, hiszen úgy valaki önmagának lenne az őse.
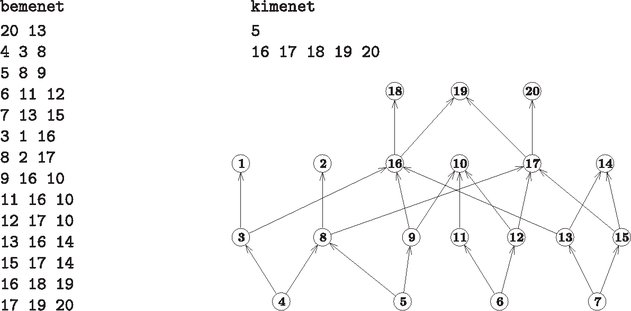
A feladathoz mellékelt példa gráfja egy irányított gráf, amelynél a gyermekek csomópontjaiból élek mutatnak mindkét szülőjük csomópontjaiba. A gyermektelen személyek tehát azok, amelyek csomópontjába nem vezet él, vagyis az ábrán a 4, 5, 6, 7 sorszámú emberek. Az ő őseik azok, akikhez tőlük az irányított gráfban el lehet jutni, míg a közös őseik azok, akikhez mindegyikőjüktől el lehet jutni. A feladat egyszerűen megoldható a következő gondolatmenet szerint:
| 1. | megkeressük a gyermektelen sorszámú személyeket; |
| 2. | minden gyermektelen személytől indítunk egy bejárást, és följegyezzük, hogy melyik csúcsokhoz lehet tőle eljutni; |
| 3. | összevetjük a 2. pontban kapott eredményeket, és megadjuk azokat a személyeket, ahová mindegyik bejárás során eljutottunk. |
A feladatot ezzel megoldottuk, de gondolkozzunk el azon, hogy mennyire hatékony a megoldásunk. A feladatban legföljebb 10 000 személy szerepel, amelyek között egy-egy konkrét példában akár több száz gyermektelen is lehet, így a 2. pontban több százszor kell bejárni egy, akár ezer csúcsot tartalmazó gráfot. Ez sajnos azzal járhat, hogy a megoldásunk jó, de nem fut le a feladathoz megadott 0,5 másodperc alatt. Vajon honnan tudhatnánk előre, hogy elég gyors lesz-e tetszőleges bemenetre a megoldásunk? Vagy megírjuk a programot és kipróbáljuk, vagy becslést adunk a lehetséges futásidőre, tehát végiggondoljuk a leendő programunk memóriahasználatát és lépésszámát. Tegyük most először ezt:
A bemenetről megkapjuk a gyermek ‐ szülő1 ‐ szülő2 számhármasokat, amelyekből fölépítjük az irányított gráfot. Legyen egy N sorból és két oszlopból álló él táblázat, amelynek i-edik sorában az i-edik személy két szülőjének sorszáma szerepel. A táblázatban szereplő pozitív érték jelentse a szülők sorszámát, a nulla vagy negatív érték azt, hogy nem rendelkezik szülőkkel (a táblázat M számú sorában lesz pozitív érték). A 10 000-es számkör egészei elférnek két bájton, a táblázat 20 000 egészet tartalmaz, tehát 40 KiB elegendő lesz a gráf éleinek tárolásához a memóriában.
A gyermektelen tulajdonság jelölésére fölveszünk egy gytn nevű, szintén N méretű táblázatot, amelyben elég egy logikai érték tárolása, ami egyszerűen elfér N bájton, így legföljebb 10 KiB-ot foglal. A táblázatot az él táblázat alapján tudjuk kitölteni: kezdetben minden személy gyermektelen, majd végigjárjuk az él táblázatot, és aki megjelenik szülőként, annál módosítjuk a gyermektelen tulajdonságot.
gytn_jelölés
gytn[] := igaz
Ciklus személy := 1-től N-ig
Ha él[személy][1]>0 akkor
gytn[él[személy][1]] := hamis
gytn[él[személy][2]] := hamis
Elágazás vége
gytn_jelölés vége
Az előbbi algoritmus futásidejét a következőképp becsülhetjük. Az első sorban a teljes gytn táblázat feltöltése valójában N értékadás, tehát N elemi lépés. A második sorban induló ciklus szintén N-szer végez feltételvizsgálatot, és nyilván kevesebb, mint N-szer két értékadást. Azt mondhatjuk, hogy a teljes programrész futási ideje N értékével egyenesen arányos, vagyis a bemenet elemszámának lineáris függvénye. Az arányossági tényező és a lineáris függvény pontos alakja attól függ, hogy mennyi idő alatt végez el egy elemi műveletet a futtató számítógép, mennyi időbe telik egy értékadás, egy összehasonlítás, egy vezérlésátadás. Ezek a részletek számunkra nem fontosak, de annyit biztosan állíthatunk, hogy bármely számítógépen futtatva a fenti programrészletet a futási idő és N értéke között lineáris kapcsolatot találnánk.
Az előbbi megfontolás alapján N-nel arányos futásidejű az a programrész is, amely még a gytn_jelölés előtt fut le azért, hogy nullázza az él táblázatot, majd beolvassa a standard bemenetről a kapott adatokat és kitöltse az él táblázatot a beolvasott adatok alapján. Bár a beolvasás feltehetőleg hosszabb időt igényel, mint egy memóriaművelet vagy egy számítás a processzorban, de a lépésszám most is a bemenettel egyenesen arányos. Ezek alapján a megoldás 1. részének becsült futás ideje a bemenet N elemszámának lineáris függvénye.
Foglalkozzunk a megoldás tervének 2. és 3. részével. Válasszuk a szélességi bejárás nem rekurzív változatát a gyermektelen csúcsoktól induló bejáráshoz. Vegyünk föl egy ős tömböt, amelynek elemei logikai értékek, és a k-adik elem megadja, hogy a k sorszámú csúcs lehet-e az eddigi bejárások alapján közös ős. A bejárások kezdése előtt a tömbben adjuk meg, hogy a gyermektelenek nem lehetnek ősök, a többiek igen. Minden bejárás után a jártunk tömb és az ős tömb elemei közötti logikai és művelet eredményét írjuk az ős tömbbe. Az első bejárás után az ős tömb maga a jártunk tömb lesz, vagyis megmutatja, hogy melyek az elsőnek választott gyermektelen személy ősei. A következő bejárás után az első két gyermektelen közös ősei esetén lesz az ős tömb egy eleme igaz, és így tovább. Az összes bejárás után megkapjuk, hogy mely csúcsok lesznek közös ősök, vagyis melyek azok, amelyekhez minden bejáráskor elértünk.
A szélességi bejárás a korábbiakhoz hasonlóan egy sor segítségével történik, amelybe először csak a bejárás kezdő csúcsa van. A bejárás csak annyiban tér el a korábban ismertetett változattól, hogy minden csúcsból vagy két él indul ki, vagy egy sem. Egy bejárás során a sorba kevesebb, mint N csúcs kerül, így a sor memóriaigénye legföljebb 2N, vagyis kevesebb, mint 20 KiB.
Családfa
él_tömb_elkészítése
gytn_jelölés
Ciklus sz := 1-től N-ig
ős[sz] := nem gytn[sz]
Ciklus vége
Ciklus k := 1-től N-ig
Ha gytn[k] akkor
jártunk[] := hamis
Sor_legyen_üres
Sorba(k)
jartunk[k] = igaz
Ciklus amíg Sor nem üres
Sorból(személy)
jártunk[személy] := igaz
Ha él[személy][1]>0 akkor
szülő1 := él[személy][1]
szülő2 := él[személy][2]
Ha nem jártunk[szülő1] akkor Sorba(szülő1) ; jártunk[szülő1] := igaz
Ha nem jártunk[szülő2] akkor Sorba(szülő2) ; jártunk[szülő1] := igaz
Elágazás vége
Ciklus vége
ős[] := ős[] és jártunk[]
Elágazás vége
Ciklus vége
Családfa vége
Becsüljük meg a Családfa algoritmus futásidejét. A k változójú ciklus előtti részről láttuk, hogy N-nel arányos lépésszámú, míg a k változójú ciklus N-szer fut le, de lényegi műveletvégzés csak azokban az esetekben történik, amikor a k-adik csúcs gyermektelen személyt jelöl.
Legyen egy tesztesetben g számú gyermektelen (1≤g≤N). Mivel a jártunk tömb hamis értékkel történő feltöltése, valamint a bejárás után az ős és a jártunk tömb elemei közötti és művelet N lépést igényel, így a k változójú ciklus lépésszáma legalább g⋅2N. Ebben a ciklusban van még a szélességi bejárás is, melynek futásideje attól függ, hogy az induló csúcstól mekkora része járható be a gráfnak. Adott N és g mellett a bejárás a gyermektelen csúcsot, valamint még legföljebb N-g számú további csúcsot jár be, helyez a sorba, azaz a bejárás N-g-vel arányos lépésszámú. A bemenetek elég különbözőek lehetnek, így a k indexű ciklus lépésszáma g⋅(N+N+N-g)-vel arányos, amit a számtani-mértani egyenlőtlenség segítségével könnyen felülről becsülhetünk: Előfordulhat tehát, hogy a tesztesetek egy részében algoritmusunk N2-tel arányos lépésszámú műveletet végez, vagyis a futásidő a bemenet elemszámának négyzetes függvénye. Ilyen gráfot nem is olyan nehéz készíteni, pl. N=2⋅g-1 csúcsot rendezzünk el úgy, hogy g számú testvérnek azonos a két szülője, és minden további szülőnek azonos a két szülője (a feladat kitűzésénél szereplő megjegyzés szerint nem csak a megszokott családi kapcsolatok lehetségesek). Így a g gyermektelentől kiindulva az algoritmusunk g-szer bejárja ugyanazt a szülőkből álló N-g csúcsú gráfot, tehát csak a bejárás lépésszáma az előzőekhez hasonlóan közelítéssel N2-tel arányos.
Összefoglalva megállapíthatjuk a becslés alapján, hogy az elkészített algoritmus legrosszabb esetben is N2-tel arányos lépésszámú, tehát N<100 esetén legföljebb 10 000-es nagyságrendű elemi műveletet hajt végre, vagyis várhatóan gyorsan lefut egy mai számítógépen. De N=10000 esetén a lépésszám már 108-nal arányos, vagyis a 100-nál kisebb esetek lépésszámának 10 000-szerese is lehet. Abban már nem lehetünk benne biztosak, hogy ilyen elemszám mellett is befejeződik az algoritmus az előírt idő alatt. A feladatra kapható teljes pontszám megszerzéséhez érdemes volna egy hatékonyabb, kisebb lépésszámú algoritmust kitalálnunk.
Persze kérdés, hogy létezik-e lényegesen jobb, nem N2-tel arányos lépésszámú megoldás. Ha a versenyen a kész programunk minden bemenetre megkapja az elérhető összes pontot, akkor nem érdemes tovább töprengeni. A következő számban bemutatunk egy ,,kicsit'' jobb megoldást, de előtte arra kérjük olvasóinkat, hogy találjanak ki a most megismertnél ügyesebb algoritmust. Az ötleteket a KöMaL fórumban az Informatika OKTV rovatban várjuk. |
 PDF | MathML
PDF | MathML