Cím:	Megoldásvázlatok a 2016/1. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Koncz Levente
Füzet:	2016/február, 75 - 83. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Ágoston és Benedek egy-egy marék kavicsot tartanak a kezükben. Ha Benedek a sajátjai közül $10$ kavicsot átadna Ágostonnak, akkor a kezükben tartott kavicsok számának szorzata $150$-nel csökkenne. Ha Benedek nem $\mathrm{10,}$ hanem $20$ kavicsot adna át Ágostonnak, akkor a kezükben tartott kavicsok számának szorzata a harmadára csökkenne. Hány kavicsot tartottak a kezükben kezdetben?   (12 pont)   Megoldás. Jelölje kezdetben Ágoston kavicsainak számát $a$, Benedek kavicsainak számát $b$. A feladat szövege alapján felírható egyenletrendszer: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \left(a+10\right)\left(b-10\right)}& {\displaystyle =ab-\mathrm{150,}}\hfill \\ \hfill {\displaystyle \left(a+20\right)\left(b-20\right)}& {\displaystyle =\frac{ab}{3}\mathrm{.}}\hfill \end{array}}\}}\end{array}$ Az első egyenlet bal oldalán elvégezve a kijelölt szorzást, majd 10-zel osztva és rendezve $a=b+5$ adódik. Ezt behelyettesítve a második egyenletbe, majd 3-mal beszorozva: $\begin{array}{c}{\displaystyle 3\left(b+25\right)\left(b-20\right)=\left(b+5\right)b\mathrm{.}}\end{array}$ A műveleteket elvégezve, 2-vel osztva és nullára rendezve a $b^2+5b-750=0$ egyenletet kapjuk. Ennek az egyenletnek a gyökei $b_1=25$ és $b_2=-30$. A negatív gyök nyilván nem megoldása a feladatnak. Ellenőrzés. Ha Benedeknek kezdetben 25 kavicsa volt, akkor Ágoston $25+5=30$-at tartott a kezében, ezek szorzata 750. Ha Benedek 10 kavicsot átad Ágostonnak, akkor kavicsaik számának szorzata $15\cdot 40=600$ lesz, tehát valóban 150-nel csökkent. Ha nem 10, hanem 20 kavicsot ad át, akkor a szorzat $5\cdot 50=250$ lesz, tehát valóban harmadára csökken. Tehát kezdetben Benedeknek 25, Ágostonnak 30 kavics volt a markában.   2. Határozzuk meg az $x$ értékét úgy, hogy az $x^2+x-2$, az $2x^2+x+3$ és a $4x^2-12$ kifejezések értéke ebben a sorrendben egy $a)$ számtani; $b)$ mértani sorozat három egymást követő tagja legyen.  (13 pont)   Megoldás. $a)$ Ha a három kifejezés értéke számtani sorozatot alkot, akkor $\begin{array}{c}{\displaystyle \left(x^2+x-2\right)+\left(4x^2-12\right)=2\left(2x^2+x+3\right)\mathrm{.}}\end{array}$ Rendezve: $x^2-x-20=0$. Az egyenlet megoldásai $x_1=5$ és $x_2=-4$. Ellenőrzés. Az első esetben a sorozat 28; 58; 88, a második esetben pedig 10; 31; 52, mindkettő jó. Tehát $x$ értéke 5 vagy $-4$ lehet. $b)$ Ha a három kifejezés értéke mértani sorozatot alkot, akkor $\begin{array}{c}{\displaystyle \left(x^2+x-2\right)\left(4x^2-12\right)={\left(2x^2+x+3\right)}^2\mathrm{.}}\end{array}$ Elvégezve a kijelölt műveleteket: $\begin{array}{c}{\displaystyle 4x^4+4x^3-20x^2-12x+24=4x^4+4x^3+13x^2+6x+9.}\end{array}$ Rendezve: $0=33x^2+18x-15=3\left(11x^2+6x-5\right)$. Az egyenlet megoldásai $x_1=-1$ és $x_2=\frac{5}{11}$. Ellenőrzés. Az első esetben a sorozat $-2$; 4; $-8$, a második esetben pedig $-\frac{162}{121}$; $\frac{468}{121}$; $-\frac{1352}{121}$ (ekkor a hányados $-\frac{26}{9}$), mindkettő jó. Tehát $x$ értéke $-1$ vagy $\frac{5}{11}$ lehet.   3. $a)$ Legyen $a$ és $b$ egy-egy olyan egész szám, amelyeket véletlenszerűen választunk a $\left[-10;10\right]$ intervallumból. Mekkora a valószínűsége, hogy az $y=ax+b$ egyenletű egyenes áthalad a $P\left(2;6\right)$ ponton? $b)$ Legyen $G$ egy hétpontú teljes gráf, csúcsai $P$, $Q$, $R$, $S$, $T$, $U$ és $V$. Hány olyan négypontú köre van $G$-nek, amely $P$ és $Q$ közül legalább az egyik csúcson áthalad?  (13 pont)   Megoldás. $a)$ Mivel $a$ és $b$ értéke is egymástól függetlenül 21-féle lehet, az összes esetek száma 441. Kedvező esetet akkor kapunk, amikor $P$ rajta van az egyenesen, tehát $6=2a+b$, azaz $a=3-\frac{b}{2}$. Ha $b$ páratlan, akkor $a$ értékére nem egész szám adódik, tehát ekkor nincs megoldás. Ha $-10\le b\le 10$ és $b$ páros, akkor egyrészt $a$ egész, másrészt $-2\le a=3-\frac{b}{2}\le 8$, tehát minden $-10$ és 10 közötti páros $b$ értékhez tartozik egy-egy jó $a$ érték, azaz 11 kedvező eset van. A keresett valószínűség ezért $\frac{11}{441}\approx 0\mathrm{,}025$. $b)$ I. megoldás. A gráf négy kiválasztott pontja három különböző négypontú kört határoz meg, mert háromféleképpen lehet kiválasztani a körben egymással nem szomszédos csúcspárokat. A $P$ csúcshoz az $R$, $S$, $T$, $U$ és $V$ csúcsok közül $\left(\genfrac{}{}{0ex}{}{5}{3}\right)=10$-féleképpen választhatunk ki másik hármat egy $P$-t igen, de $Q$-t nem tartalmazó négypontú körhöz. Hasonlóképpen a $Q$ csúcshoz is 10-féleképpen választhatunk ki másik hármat egy $Q$-t igen, de $P$-t nem tartalmazó négypontú körhöz. Végül egy $P$-t és $Q$-t is tartalmazó négypontú körhöz $\left(\genfrac{}{}{0ex}{}{5}{2}\right)=10$-féleképpen választhatunk ki másik kettőt a maradék öt csúcs közül. Mivel mind a 30 lehetséges pontnégyes három különböző négypontú kört határoz meg, így a feltételeknek megfelelő körök száma 90. II. megoldás. A gráf négy kiválasztott pontja három különböző négypontú kört határoz meg, mert háromféleképpen lehet kiválasztani a körben egymással nem szomszédos csúcspárokat. A gráf pontjai közül $\left(\genfrac{}{}{0ex}{}{7}{4}\right)=35$-féleképpen választhatunk ki négyet egy négypontú körhöz. Ezen pontnégyesek számából levonjuk a rossz pontnégyesek számát, melyek sem $P$-t, sem $Q$-t nem tartalmazzák. Az ilyen pontnégyesek száma $\left(\genfrac{}{}{0ex}{}{5}{4}\right)=5$, tehát összesen $35-5=30$ megfelelő pontnégyes van. Mivel mind a 30 lehetséges pontnégyes három különböző négypontú kört határoz meg, így a feltételeknek megfelelő körök száma 90.   4. $a)$ Mi lehet az alapszáma annak a számrendszernek, melyben teljesül az alábbi egyenlőtlenség? $\begin{array}{c}{\displaystyle 1410<1254+135.}\end{array}$ $b)$ Egy $n$ elemű halmaznak feleannyi $7$ elemű részhalmaza van, mint $8$ elemű. Határozzuk meg az $n$ értékét.  (13 pont)   Megoldás. $a)$ Mivel az egyenlőtlenségben szereplő legnagyobb számjegy az 5, ezért a számrendszer $n$ alapszámára $n\ge 6$ teljesül (és $n\in \text{Z}$). Az $n$ alapú számrendszer helyiértékei jobbról balra 1, $n$, $n^2$ és $n^3$, ezért az egyenlőtlenség így írható: $\begin{array}{c}{\displaystyle n^3+4n^2+n<\left(n^3+2n^2+5n+4\right)+\left(n^2+3n+5\right)\mathrm{.}}\end{array}$ Rendezve: $n^2-7n-9<0$. A megfelelő másodfokú egyenlet gyökei: $\begin{array}{c}{\displaystyle n_1=\frac{7+\sqrt[]{85}}{2}\approx 8\mathrm{,}1\text{és}{n}_2=\frac{7-\sqrt[]{85}}{2}\approx -1\mathrm{,}1.}\end{array}$ Mivel a másodfokú kifejezés főegyütthatója pozitív, ezért az egyenlőtlenség $n_1<n<n_2$ esetén teljesül. Figyelembe véve még a megoldás elején kapott feltételt is, a számrendszer alapszáma 6, 7 vagy 8 lehet. $b)$ Az $n$ elemű halmaz $k$ elemű részhalmazainak száma $\left(\genfrac{}{}{0ex}{}{n}{k}\right)$. Ha a halmaznak feleannyi 7 elemű részhalmaza van, mint 8 elemű, akkor $\begin{array}{c}{\displaystyle \frac{1}{2}=\frac{\left(\genfrac{}{}{0ex}{}{n}{7}\right)}{\left(\genfrac{}{}{0ex}{}{n}{8}\right)}=\frac{\frac{n!}{7!\cdot \left(n-7\right)!}}{\frac{n!}{8!\cdot \left(n-8\right)!}}=\frac{n!}{7!\cdot \left(n-7\right)!}\cdot \frac{8!\cdot \left(n-8\right)!}{n!}=\frac{8}{n-7}\mathrm{,}}\end{array}$ ahonnan $n=23$. Ellenőrzés. A 23 elemű halmaz 7 elemű részhalmazainak száma $\left(\genfrac{}{}{0ex}{}{23}{7}\right)=245157$, ez valóban fele a 8 elemű részhalmazok számának, mely $\left(\genfrac{}{}{0ex}{}{23}{8}\right)=490314$.   II. rész     5. Három testvér betér egy fagylaltozóba. Nyolcféle fagylalt kapható: citrom, csokoládé, eper, karamell, meggy, puncs, sárgabarack és vanília. (Az alábbi kérdéseknél a gombócok sorrendjétől minden esetben eltekintünk.) $a)$ Tünde három különböző ízű gombócot szeretne kérni. A puncsot nem szereti, ezért azt biztosan nem kér, a citrom viszont a kedvence, ha van, azt sosem mulasztja el. Hányféleképpen választhat Tünde? $b)$ Viola is háromgombócos fagyit eszik, de csak a csokoládét, a karamellt, a puncsot és a vaníliát szereti. Hányféleképpen választhat Viola, ha egy-egy ízből akár több gombóccal is ehet? $c)$ Zolinak mindegy, mit kap, ezért csak annyit mond a fagylaltosnak, hogy három különböző ízt szeretne. Mennyi a valószínűsége annak, hogy a három gombóc közül pontosan kettő gyümölcsízű (citrom, eper, meggy vagy sárgabarack) lesz? (A fagylaltos a három gombóc ízét egymástól függetlenül, véletlenszerűen választja ki.) $d)$ Egy jó közelítéssel forgáskúp alakú tölcsér alapkörének belső átmérője 58 mm, magassága 83 mm. Hány dkg 0,6 g/cm${}^3$ sűrűségű fagylalt fér ebbe a tölcsérbe, ha színültig töltjük?  (16 pont)   Megoldás. $a)$ Hat lehetséges íz közül kell kiválasztani két különbözőt úgy, hogy a kiválasztott ízek sorrendje nem számít. A lehetséges kiválasztások száma $\left(\genfrac{}{}{0ex}{}{6}{2}\right)=21$. $b)$ I. megoldás. Ha három különböző ízt kér, akkor 4 lehetősége van (aszerint, hogy melyiket hagyja ki). Ha két különbözőt kér, akkor 4-féleképpen választhatja ki azt az ízt, amelyből két gombócot is kér, s e mellé 3-féleképpen a másikat. Ez összesen $4\cdot 3=12$ különböző lehetőséget jelent. Ha csak egyféle ízt kér, akkor ismét 4 lehetősége van. Összesen tehát $4+12+4=20$-féleképpen kérhet a feltételeknek megfelelően. II. megoldás. 4 íz közül kell kiválasztani hármat úgy, hogy a kiválasztott ízek sorrendje nem számít, de egy-egy ízt többször is kiválaszthat. Ez megfelel 4 elem harmadosztályú ismétléses kombinációjának. A lehetőségek száma így $\left(\genfrac{}{}{0ex}{}{4+3-1}{3}\right)=\left(\genfrac{}{}{0ex}{}{6}{3}\right)=20$. $c)$ I. megoldás. Négy gyümölcsíz közül kell kettőt, és a négy nem gyümölcsíz közül egyet kiválasztani (a sorrendre való tekintet nélkül). A kedvező esetek száma így $\left(\genfrac{}{}{0ex}{}{4}{2}\right)\left(\genfrac{}{}{0ex}{}{4}{1}\right)=24$. Az összes eset száma: $\left(\genfrac{}{}{0ex}{}{8}{3}\right)=56$. A kérdezett valószínűség így $\begin{array}{c}{\displaystyle p=\frac{24}{56}=\frac{3}{7}\left(\approx 0\mathrm{,}429\right)\mathrm{.}}\end{array}$ II. megoldás. Legyen az első gombóc gyümölcsízű, ennek a valószínűsége $\frac{4}{8}$. Annak a valószínűsége, hogy a második gombóc is gyümölcsízű (mivel az elsőnek választott ízt már nem kaphatja), $\frac{3}{7}$. Annak a valószínűsége, hogy a harmadik gombóc nem gyümölcsízű, $\frac{4}{6}$. Mivel a három esemény egymástól független, ezért annak a valószínűsége, hogy a három gombóc közül az első kettő gyümölcsízű, a harmadik nem, az előzőek szorzata, tehát $\frac{4}{8}\cdot \frac{3}{7}\cdot \frac{4}{6}=\frac{1}{7}$. A nem gyümölcsízű gombócot ugyanekkora valószínűséggel kaphatja elsőként vagy másodikként is, így a keresett valószínűség ennek az értéknek a háromszorosa, tehát $\frac{3}{7}\left(\approx 0\mathrm{,}429\right)$. $d)$ $r=2\mathrm{,}9$ cm, $m=8\mathrm{,}3$ cm. A tölcsér térfogata $V=\frac{2\mathrm{,}{9}^2\cdot \pi \cdot 8\mathrm{,}3}{3}\left(\approx 73\mathrm{,}1{\text{cm}}^3\right)$. Ebbe a tölcsérbe így (színültig töltve) $m=\rho V\approx 43\mathrm{,}9$ g, azaz kb. 4,4 dkg fagylalt fér.   6. Egy 20 cm sugarú körbe írt $ABC$ hegyesszögű háromszög két oldala $AC=34$ cm és $BC=30$ cm. $a)$ Határozzuk meg a háromszög $AB$ oldalának hosszát. $b)$ Határozzuk meg a háromszög $B$ csúcsához tartozó szögfelezőjének és súlyvonalának hosszát.  (16 pont) 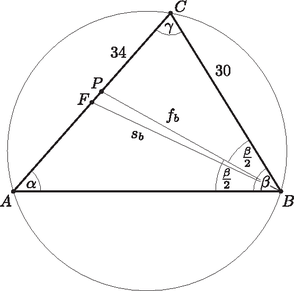  Megoldás. $a)$ Jelöljük a háromszög szögeit a szokott módon $\alpha$-val, $\beta$-val, illetve $\gamma$-val. Az ismert $a=2r\cdot \text{sin}\alpha$ képlet alapján $\begin{array}{c}{\displaystyle \text{sin}\alpha =\frac{30}{2\cdot 20}=0\mathrm{,}\mathrm{75,}}\end{array}$ ahonnan $\alpha \approx 48\mathrm{,}{6}^{\circ }$ (hiszen hegyesszög).     $\text{sin}\beta =0\mathrm{,}85$, ahonnan $\beta \approx 58\mathrm{,}{2}^{\circ }$ (hiszen hegyesszög). Innen $\begin{array}{c}{\displaystyle \gamma ={180}^{\circ }-\alpha -\beta \approx 73\mathrm{,}{2}^{\circ }\mathrm{,}}\end{array}$ majd $\begin{array}{c}{\displaystyle AB=2\cdot 20\cdot \text{sin}73\mathrm{,}{2}^{\circ }\approx 38\mathrm{,}3\text{cm. }}\end{array}$ $b)$ Az $AC$ oldal felezőpontját $F$-fel jelölve a $B$ csúcsból induló súlyvonal hossza ($s_b$) kiszámítható a $BCF$ háromszögből koszinusztétellel: $\begin{array}{c}{\displaystyle s_b=\sqrt[]{{30}^2+{17}^2-2\cdot 30\cdot 17\cdot \text{cos}\gamma }\approx 29\mathrm{,}9\text{cm. }}\end{array}$ A $B$-ből induló szögfelező metszéspontját az $AC$ oldallal jelölje $P$. $\begin{array}{c}{\displaystyle CPB\sphericalangle ={180}^{\circ }-\frac{\beta }{2}-\gamma \approx 77\mathrm{,}{7}^{\circ }\mathrm{.}}\end{array}$ A $B$-ből induló szögfelező hossza ($f_b$) ezután kiszámítható a $BCP$ háromszögből szinusztétellel: $\begin{array}{c}{\displaystyle \frac{f_b}{30}=\frac{\text{sin}\gamma }{\text{sin}CPB\sphericalangle }\mathrm{,}\text{ahonnan}{f}_b\approx 29\mathrm{,}4\text{cm. }}\end{array}$   7. Van hatféle számkártyánk, mindegyikből 1-1 darab: 1, 2, 3, 4, 5, 6. A kártyákat véletlenszerűen sorba rendezve hatjegyű számokat képezünk. $a)$ Igazoljuk, hogy $\frac{4}{15}$ annak a valószínűsége, hogy az így kapott szám osztható lesz $12$-vel. $b)$ Határozzuk meg annak a valószínűségét, hogy az így kapott szám a 6-os számjeggyel kezdődik, feltéve, hogy $12$-vel osztható. $c)$ Egy papírlapra felírjuk a számkártyákból képezhető összes lehetséges hatjegyű számot. Határozzuk meg a papírlapra felírt számok mediánját.  (16 pont)   Megoldás. $a)$ 12-vel akkor osztható egy szám, ha 3-mal és 4-gyel is osztható. A képzett szám 3-mal biztosan osztható lesz, mert (a kártyák sorrendjétől függetlenül) számjegyeinek összege 21 (ami osztható 3-mal). 4-gyel akkor osztható egy szám, ha az utolsó két számjegyéből képzett szám osztható 4-gyel. Az utolsó két helyre ezért a következő kártyák kerülhetnek: 12, 32, 52, 24, 64, 16, 36, 56, ez 8 lehetőség. Az utolsó két helyre az összes lehetőség: $6\cdot 5=30$. Mivel minden esetben ugyanannyiféle lehet az első négy számjegy, a keresett valószínűség $\frac{8}{30}=\frac{4}{15}$. $b)$ Jelölje $A$ azt az eseményt, hogy a kapott szám 6-ossal kezdődik, $B$ pedig azt az eseményt, hogy 12-vel osztható. Ezzel a jelöléssel meghatározandó a $P\left(A\mid B\right)$ valószínűség. A feltételes valószínűség definíciója szerint $\begin{array}{c}{\displaystyle P\left(A\mid B\right)=\frac{P\left(AB\right)}{P\left(B\right)}\mathrm{.}}\end{array}$ Tudjuk, hogy $P\left(B\right)=\frac{4}{15}$. Határozzuk meg $P\left(AB\right)$-t: ha a kapott szám 6-ossal kezdődik, akkor 12-vel csak akkor lehet osztható, ha az utolsó két számjegyéből képzett szám 12, 32, 52 vagy 24. A második, harmadik és negyedik számjegy mind a négy esetben $3!=6$-féle lehet. Összesen tehát $6\cdot 4=24$ ilyen szám van. Az összes felírható szám $6!=720$. Tehát $\begin{array}{c}{\displaystyle P\left(AB\right)=\frac{24}{720}=\frac{1}{30}\mathrm{.}}\end{array}$ Ezért $\begin{array}{c}{\displaystyle P\left(A\mid B\right)=\frac{\frac{1}{30}}{\frac{4}{15}}=\frac{1}{8}\mathrm{.}}\end{array}$ $c)$ 720 darab ilyen szám van, a medián ezért a nagyság szerint sorba rendezett számok közül a két középső átlaga. Nagyság szerint a két középső szám a legnagyobb 3-mal és a legkisebb 4-gyel kezdődő szám lesz, ezek a 365 421 és a 412 356, ezért a medián $\begin{array}{c}{\displaystyle \frac{365421+412356}{2}=\frac{777777}{2}=388888\mathrm{,}5.}\end{array}$   8. Gyurta Dániel $2009$-ben, Rómában szerezte első világbajnoki aranyérmét a $200$ méteres mellúszásban. Győztes ideje 2:07.64 volt $(2$ perc $7$ másodperc $64$ századmásodperc$)$. Egyetlen századmásodperccel előzte meg az amerikai Eric Shanteau-t. $a)$ Határozzuk meg Gyurta Dániel átlagsebességét a teljes távon. A választ km/h-ban, egy tizedesjegy pontossággal adjuk meg. $b)$ Az úszók rendszerint gyorsabbak a táv elején. Gyurta Dániel a második $100$ métert 1:05.50 alatt tette meg. Ezen belül az utolsó $50$ méter megtételéhez $10$ századmásodperccel több időre volt szüksége, mint a megelőző $50$ méter megtételéhez. Határozzuk meg Gyurta Dániel idejét az utolsó $50$ méteren. $c)$ Eric Shanteau az első $100$ métert 1:01.22, a második $100$ métert 1:06.43 alatt tette meg. Gyurta Dániel célba érkezésekor az amerikai úszónak még hány centiméter volt hátra a teljes távból? (Tételezzük fel, hogy a második $100$ métert egyenletes tempóban tette meg a versenyző.) A választ egy tizedesjegy pontossággal adjuk meg. $d)$ Hugó, Hanna és Ödön, a három testvér ugyanabba az uszodába járnak úszóedzésre. Hugó (a legkisebb) a $20$ méteres, Hanna a $33\frac{1}{3}$ méteres, Ödön az $50$ méteres medencében edz. Az egyik edzésen Hanna néggyel több hosszt úszott, mint Ödön, Hugó pedig néggyel több hosszt úszott, mint Hanna. A Hugó, Hanna és Ödön által leúszott távolságok (ebben a sorrendben) egy növekvő számtani sorozat szomszédos tagjai. Határozzuk meg mindhárom gyerek esetén az edzésen általa leúszott távolságot.  (16 pont)   Megoldás. $a)$ 2 perc 7 másodperc 64 századmásodperc = 127,64 másodperc$=\frac{127\mathrm{,}64}{3600}$ óra, $\text{200 m = 0,2 km}$. Gyurta Dániel átlagsebessége $\begin{array}{c}{\displaystyle \frac{0\mathrm{,}2}{\frac{127\mathrm{,}64}{3600}}=\frac{720}{127\mathrm{,}64}\approx 5\mathrm{,}6\text{ km/h}\text{volt.}}\end{array}$ $b)$ $x=\frac{1:05.50-0:00.10}{2}=\frac{1:05.40}{2}=\frac{65.40}{2}=32.70$ az ideje a harmadik, 32.80 pedig az utolsó 50 méteren. 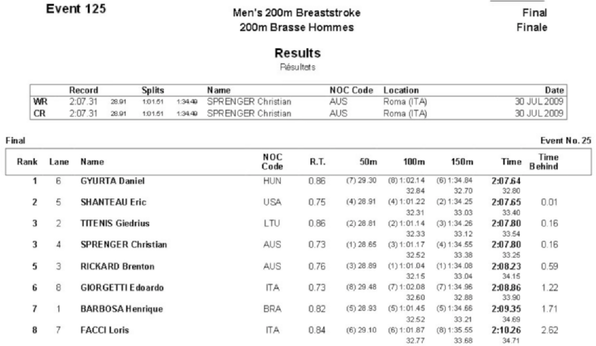    $c)$ Shanteau a második 100 métert (egyenletes tempóban) 66 másodperc 43 századmásodperc, tehát 6643 századmásodperc alatt tette meg. Gyurta Dániel célba érkezésekor még 1 századmásodpercnyi útja, azaz $\begin{array}{c}{\displaystyle \frac{100}{6643}\approx 0\mathrm{,}015\text{ méter}=1\mathrm{,}5\text{ cm}}\end{array}$ volt hátra. $d)$ I. megoldás. A Hanna által leúszott hosszok számát jelölje $n$, ekkor Hugó $n+4$, Ödön pedig $n-4$ hosszt úszott. Ekkor Hugó $20\left(n+4\right)$, Hanna $33\frac{1}{3}n$, Ödön pedig $50\left(n-4\right)$ métert úszott. A feladat szövege szerint ez a három távolság számtani sorozatot alkot, így $\begin{array}{c}{\displaystyle 50\left(n-4\right)+20\left(n+4\right)=2\cdot 33\frac{1}{3}n\mathrm{.}}\end{array}$ Innen $3\frac{1}{3}n=120$, azaz $n=36$. Hugó 40, Hanna 36, Ödön 32 hosszt úszott, az általuk leúszott távolságok pedig rendre 800, 1200 és 1600 méter. Ezek a távolságok valóban számtani sorozatot alkotnak. II. megoldás. A Hanna által leúszott távolságot $m$-mel, a számtani sorozat differenciáját $d$-vel jelölve megoldandó a $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 20\left(m+4\right)}& {\displaystyle =m-d}\hfill \\ \hfill {\displaystyle 33\frac{1}{3}m}& {\displaystyle =m}\hfill \\ \hfill {\displaystyle 50\left(m-4\right)}& {\displaystyle =m+d}\hfill \end{array}}\}}\end{array}$ egyenletrendszer. Az első egyenlet ötszöröséből kivonva a második egyenlet háromszorosát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle 400=2m-5d\mathrm{.}}& \text{(<mn>1</mn>)}\end{array}}$ A harmadik egyenlet kétszereséből kivonva a második egyenlet háromszorosát: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle -400=-m+2d\mathrm{.}}& \text{(<mn>2</mn>)}\end{array}}$ Az (1) egyenlethez hozzáadva a (2) egyenlet kétszeresét $d=400$ adódik, amit visszahelyettesítve (1)-be kapjuk, hogy $m=1200$, majd ezeket az értékeket az eredeti egyenletrendszer valamelyik egyenletébe helyettesítve $n=36$ adódik. Hugó 40, Hanna 36, Ödön 32 hosszt úszott, az általuk leúszott távolságok pedig rendre 800, 1200 és 1600 méter. Ezek a távolságok valóban egy (400 differenciájú) számtani sorozatot alkotnak.   9. Egy duatlon verseny rajtja egy egyenes tengerparton van, célja a vízben. Egyik lehetőség a táv teljesítésére, hogy először 4 km-t fut a versenyző a parton, majd $90$ fokkal elfordulva 1 km-t úszik a tengerben. Azonban megengedett bármikor letérni a futópályáról és úszni kezdeni a cél felé. $a)$ Mennyi idő alatt ér célba Dénes, akinek a tengerparti homokban futva 8 km/h, a vízben úszva 1,5 km/h a sebessége, és 3,5 km lefutása után kezd el úszni a cél felé? $b)$ Juli sebessége futva 6 km/h, úszva 2 km/h. A 4 km-es futópálya vége előtt hány méterrel érdemes úszni kezdenie ahhoz, hogy a lehető leggyorsabban teljesítse a távot? Mekkora ez az idő?  (16 pont)   Megoldás. $a)$ Dénesnek úszva $s_{\text{ú}}=\sqrt[]{1^2+0\mathrm{,}{5}^2}\approx 1\mathrm{,}118$ km-t kell megtennie, ehhez $t_{\text{ú}}=\frac{s_{\text{ú}}}{v_{\text{ú}}}=\frac{1\mathrm{,}118}{1\mathrm{,}5}\approx 0\mathrm{,}745$ órára van szüksége. A 3,5 km lefutásához szükséges idő $t_{\text{f}}=\frac{s_{\text{f}}}{v_{\text{f}}}=\frac{3\mathrm{,}5}{8}\approx 0\mathrm{,}438$ óra. A teljes táv megtételéhez szükséges idő $t=t_{\text{f}}+t_{\text{ú}}\approx 1\mathrm{,}183$ óra, azaz kb. 71 perc. $b)$ I. megoldás. Jelölje $x$ azt a (kilométerben mért) távolságot, amennyivel a 4 km-es futópálya vége előtt Juli bevág a vízbe. Ekkor a teljes táv megtételéhez szükséges idő 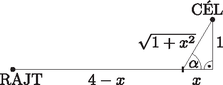$\begin{array}{c}{\displaystyle t=t_{\text{f}}+t_{\text{ú}}=\frac{4-x}{6}+\frac{\sqrt[]{1^2+x^2}}{2}\mathrm{.}}\end{array}$ Vizsgáljuk a $t\left(x\right)$ függvényt a $\left(0;4\right)$ intervallumon. A függvénynek minimumhelye ott lehet, ahol a deriváltja 0. $\begin{array}{c}{\displaystyle t\text{'}\left(x\right)=-\frac{1}{6}+\frac{1}{2}\cdot \frac{1}{2\sqrt[]{1+x^2}}\cdot 2x=\frac{x}{2\sqrt[]{1+x^2}}-\frac{1}{6}\mathrm{.}}\end{array}$     Ha $t\text{'}\left(x\right)=0$, akkor $\begin{array}{c}{\displaystyle \frac{x}{2\sqrt[]{1+x^2}}=\frac{1}{6}\mathrm{,}\text{azaz}6x=2\sqrt[]{1+x^2}\mathrm{.}}\end{array}$ Négyzetre emelve $36x^2=4\left(1+x^2\right)$, ahonnan $x^2=\frac{1}{8}$, tehát (figyelembe véve, hogy $x>0$) $x=\frac{1}{2\sqrt[]{2}}\approx 0\mathrm{,}354$ km. $\begin{array}{c}{\displaystyle t\text{'}\left(x\right)=\frac{x}{2\sqrt[]{1+x^2}}-\frac{1}{6}=\frac{1}{2}\cdot \sqrt[]{\frac{x^2}{1+x^2}}-\frac{1}{6}=\frac{1}{2}\cdot \sqrt[]{1-\frac{1}{1+x^2}}-\frac{1}{6}\mathrm{,}}\end{array}$ s innen látszik, hogy $x$ növelésével a gyök alatti törtkifejezés nevezője nő, a törtkifejezés értéke csökken, így a gyök alatti kifejezés értéke nő. A deriváltfüggvény tehát $x=\frac{1}{2\sqrt[]{2}}$-ben negatívból pozitívba megy át, így az adott helyen valóban minimuma van a $t$ függvénynek. (Behelyettesítve azt kapjuk, hogy $t\left(0\right)$ és $t\left(4\right)$ nagyobb, mint $t\left(\frac{1}{2\sqrt[]{2}}\right)$). Tehát a futópálya vége előtt kb. 354 méterrel érdemes Julinak úszni kezdenie. A táv megtételéhez szükséges idő ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle t\left(\frac{1}{2\sqrt[]{2}}\right)}& {\displaystyle =\frac{4-\frac{1}{2\sqrt[]{2}}}{6}+\frac{\sqrt[]{1+\frac{1}{8}}}{2}=\frac{2}{3}-\frac{1}{12\sqrt[]{2}}+\frac{3}{4\sqrt[]{2}}=\frac{2}{3}+\frac{8}{12\sqrt[]{2}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{2}{3}\left(1+\frac{1}{\sqrt[]{2}}\right)=\frac{2+\sqrt[]{2}}{3}\approx 1\mathrm{,}138\text{ óra, azaz kb. 68 perc.}}\hfill \end{array}}$ II. megoldás. Jelölje $\alpha$ azt a szöget, amit az optimális irányú úszás a futópályával bezár. Ekkor az úszás megkezdésekor a futópályából hátralevő szakasz hossza $\text{ctg}\alpha$, az úszva megteendő táv pedig $\frac{1}{\text{sin}\alpha }$. A teljes táv megtételéhez szükséges idő $\begin{array}{c}{\displaystyle t=t_{\text{f}}+t_{\text{ú}}=\frac{4-\text{ctg}\alpha }{6}+\frac{1}{2\text{sin}\alpha }\mathrm{.}}\end{array}$ Vizsgáljuk a $t\left(\alpha \right)$ függvényt a $\left(0;\frac{\pi }{2}\right)$ intervallumon. A függvénynek minimumhelye ott lehet, ahol a deriváltja 0. $\begin{array}{c}{\displaystyle t\text{'}\left(\alpha \right)=\frac{1}{6\text{sin}{}^2\alpha }-\frac{\text{cos}\alpha }{2\text{sin}{}^2\alpha }=\frac{1-3\text{cos}\alpha }{6\text{sin}{}^2\alpha }\mathrm{.}}\end{array}$ Ha $t\text{'}\left(\alpha \right)=0$, akkor $1-3\text{cos}\alpha =0$, azaz $\text{cos}\alpha =\frac{1}{3}$, tehát ${\alpha }_{\underset{}{\overset{}{\text{min}}}}\approx 70\mathrm{,}{53}^{\circ }$ (1,231 radián). Mivel $\alpha$ növelésével $\text{cos}\alpha$ csökken, a deriváltfüggvény tehát ebben a pontban negatívból pozitívba megy át, így az adott helyen valóban minimuma van a $t$ függvénynek. (Behelyettesítve azt kapjuk, hogy $t\left(0\right)$ és $t\left(\frac{\pi }{2}\right)$ nagyobb, mint $t\left(70\mathrm{,}{53}^{\circ }\right)$). Tehát a futópálya vége előtt kb. $\text{ctg}70\mathrm{,}{53}^{\circ }\approx 0\mathrm{,}354$ kilométerrel érdemes Julinak úszni kezdenie. A táv megtételéhez szükséges idő ekkor $t\left({\alpha }_{\underset{}{\overset{}{\text{min}}}}\right)\approx 1\mathrm{,}138$ óra, azaz kb. 68 perc.