Kezdőlap


Cím:	Matematika és fizika totó megoldása
Füzet:	2016/január, 41 - 44. oldal	PDF \| MathML
Hivatkozás(ok):	2016/január: Matematika és fizika totó

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A telitalálatos szelvény:

\begin{matrix} X, X, X, 2,1,2, 2, X,2, X, X, X, 1, X . \end{matrix}

A legtöbb (11) találatot Williams Kada (Szeged, Radnóti M. Kís. Gimn., 11. évf.) érte el.
Az alábbiakban rövid útmutatást adunk a feladatok megoldásához.

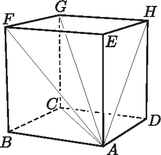
1. Legyen a kocka egy lapja

A B C D

, az ennek csúcsaiból kiinduló harmadik élek

A E

B F

C G

D H

és a kiszemelt csúcs

A

. A szimmetria miatt elég az

A B

és az

A C

élekkel bezárt szögeket vizsgálni.

A B

éllel az

A C

és az

A F

él

45^{\circ}

-os, míg az

A D

A E

és az

A H

él

90^{\circ}

-os szöget zár be. Végül az

A B

és az

A G

él által bezárt szög megegyezik az 1 és

\sqrt[]{2}

befogójú derékszögű háromszög nagyobbik szögével.
Az

A C

él az

A B

és az

A D

éllel

45^{\circ}

-os, az

A E

éllel

90^{\circ}

-os szöget zár be. Mivel a

C A F

és a

C A H

háromszög is szabályos, így az

A F

és az

A H

éllel bezárt szög egyaránt

60^{\circ}

. Végül az

A C

és az

A G

élek által bezárt szög megegyezik az 1 és

\sqrt[]{2}

befogójú derékszögű háromszög kisebbik szögével.
Tehát

5

különböző nagyságú szöget kapunk.

2. Mivel

\begin{matrix} a = 1 \frac{fényév}{{év}^{2}} = \frac{c \cdot év}{{év}^{2}} = \frac{3 \cdot 10^{8} \frac{m}{s}}{365 \cdot 24 \cdot 3600 s} = 9, 5 \frac{m}{s^{2}} \approx g, \end{matrix}

egy

m

tömegű űrhajós majdnem pontosan a földi

m g

súlyával megegyező nagyságú ,,tehetetlenségi erőt'' érez.

3. Készítsünk táblázatot.

\begin{matrix} Hány & Mitől & Meddig & Hány & A felhasznált jegyek száma \\ jegyűek & db & ebben a csoportban & eddig összesen \\ 1 & 1^{2} & 3^{2} & 3 & 3 & 3 \\ 2 & 4^{2} & 9^{2} & 6 & 12 & 15 \\ 3 & 10^{2} & 31^{2} & 22 & 66 & 81 \end{matrix}

A 100-as sorszámú számjegy a 4 jegyűekkel betöltött

100 - 81 = 19

-edik helyen áll. Mivel

19 = 4 \cdot 4 + 3

, így a kérdéses számjegy a

{(32 + 4)}^{2} = 1296

harmadik jegye, vagyis a 9-es.

4. Ha a

z

tengely függőlegesen felfelé mutat és a kezdősebesség nagysága

v_{0} = \sqrt[]{2 g h}

, akkor a parabolák csúcspontjainak mértani helyét az

x^{2} + y^{2} + {(2 z - h)}^{2} = h^{2}

egyenlet írja le. Ez egy lencseszferoidot határoz meg, melynek féltengelyei

h

h

\frac{1}{2} h

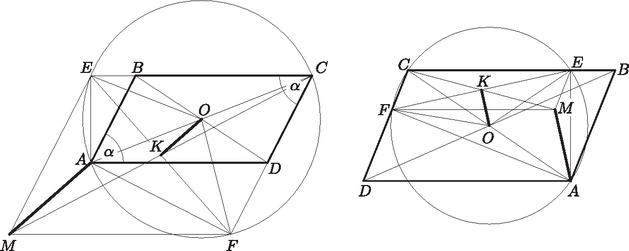
5. Az

A E F

háromszög

M E

magasságvonala merőleges

A F

-re, tehát párhuzamos

C D

-vel. Ugyanígy

M F ∥ C B

, tehát az

M E C F

négyszög paralelogramma (az ábra két változatában

B A D ∢

hegyesszög, illetve tompaszög).

Jelöljük az

M E C F

és az

A B C D

paralelogramma középpontját

K

-val, illetve

O

-val.

K O

A C M

háromszög

A M

-mel párhuzamos középvonala, tehát

A M = 2 \cdot K O

E

és

F

rajta vannak az

A C

Thalész-körén, így

O E = O F = A C / 2

, és mivel

K

E F

-et is felezi, azért

K O

O E F

egyenlő szárú háromszög magassága. Ebből

\begin{matrix} A M^{2} = 4 \cdot {K O}^{2} = 4 (O E^{2} - K E^{2}) = A C^{2} - E F^{2} . \end{matrix}

6. Ha a sötét mezők feletti kockák jó szigetelők (

ϱ_{1} \to \infty

), akkor az egész tábla is szigetelőként viselkedik (

ϱ_{0} \to \infty

), mert a véges vezetőképességű kockák csak élek (nulla nagyságú ,,felületek'') mentén érintkeznek; az (X) válasz tehát nem lehet jó. Azt is könnyen beláthatjuk, hogy ha a ,,sötét'' kockák jó vezetők (

ϱ_{1} \to 0

), akkor az egész tábla is jó vezetőként viselkedik, vagyis

ϱ_{0} \approx 0)

. Érvelésünk: a fémlapokra adott feszültséget kapcsolva a jól vezető kockák egymással érintkező éleinek közelében véges potenciálkülönbség, tehát nagy elektromos térerősség alakul ki, emiatt a véges

ϱ_{2}

fajlagos ellenállású kockák éleinek közelében nagyon nagy áram folyik. Ezek szerint az (1)-es válasz is hibás, tehát a (2)-es válasznak kell helyesnek lennie. Valóban, megmutatható (ha nem is túl egyszerűen), hogy az általános esetben mindig teljesül:

ϱ_{0} = \sqrt[]{ϱ_{1} ϱ_{2}}

7. A második egyenletből

x = 5 y - 11

. Mivel

x

feltételünk szerint negatív, az egyenlőség csak úgy teljesülhet, ha

y < \frac{11}{5}

. Az

y

-ra vonatkozó kikötésből

y = 2

vagy

y = 1

adódik, s ezért

x = - 1

vagy

x = - 6

.
Az első egyenletből az

x = - 1

y = 2

esetben

m = 4

-et kapunk, míg a másik esetben a kapott

m

érték nem egész szám.

8. Bebizonyítható, hogy (lineáris) optikai eszközökkel a felmelegített test hőmérséklete nem lehet magasabb, mint a Nap felszíni hőmérséklete. Ellenkező esetben (leegyszerűsített érveléssel) nem a Nap melegítené a testet, hanem a test a Napot. Ha viszont a Napból érkező energiát pl. akkumulátorokban elraktározzuk, majd azzal hevítünk fel egy testet, az elérhető hőmérsékletnek nincs elvi felső korlátja. Jól mutatja ezt a Nagy Hadronütköztető, amelyben elektromos energia felhasználásával nehéz atommagokat gyorsítanak fel a fénysebességhez közeli sebességekre, majd a magok összeütközése után rövid időre igen magas hőmérsékletű anyagot állítanak elő.

9. Egy kis kockának legfeljebb három lapja lehet piros, ezek a sarokkockák. Mivel ezek a legjobban festett kockák, nincs náluk jobban festett szomszédjuk, ez a

8

kocka a

b)

szempont szerint ugyanabba az osztályba tartozik.
A 0, 1 és 2 piros lappal rendelkező kockák között

n \geq 5

esetén találhatunk olyat, amelynek összes szomszédján vele megegyező számú piros lap van, és olyat is, amelynek van jobban festett szomszédja.
A nem üres osztályok száma tehát

1 + 3 \cdot 2 = 7

10. Nem az elektromos potenciál nagyságát, hanem annak egységnyi hosszra eső változási ütemét (vagyis az elektromos térerősséget) érzékelik az űrhajósok. A földi potenciál értékét nem ,,viszi magával'' az űrhajó, hiszen a potenciál nem megmaradó mennyiség, hanem az utazás során fokozatosan változik, növekszik. A helyzet mechanikai megfelelője: egy felhőkarcoló legfelső emeletének megközelítése sem veszélyes amiatt, hogy ott sokkal nagyobb a helyzeti energiánk, mint a földszinten.

11. Az összes esetek száma

6^{n}

. A kedvező esetek száma

n \cdot 5^{n - 1}

.
A keresett valószínűség

n

függvényében:

\begin{matrix} P (n) = \frac{n \cdot 5^{n - 1}}{6^{n}} = \frac{n}{6} \cdot {(\frac{5}{6})}^{n - 1} . \end{matrix}

Látszik, hogy ez

n = 5

és

n = 6

esetén megegyezik, tehát az (X) válasz a jó.
Be is bizonyítjuk, hogy ekkor van a maximum. Tekintsük

P (n + 1)

és

P (n)

hányadosát:

\begin{matrix} q (n) = \frac{P (n + 1)}{P (n)} = \frac{n + 1}{n} \cdot \frac{5}{6} = \frac{5 n + 5}{5 n + n} . \end{matrix}

Látjuk, hogy

q (5) = 1

, vagyis a

P (5)

és

P (6)

valószínűségek egyenlők. Továbbá ha

n < 5

, akkor

q (n) > 1

, azaz

P (n) < P (n + 1)

, végül ha

n > 5

, akkor

q (n) < 1

, tehát

P (n + 1) < P (n)

12. A hőtan második főtétele szerint nem létezik olyan hőerőgép, aminek a hatásfoka meghaladná a Carnot-körfolyamat

Δ T / T_{1}

hatásfokát. Mivel ez utóbbi

Δ T \to 0

határesetben nullához tart, az (1)-es és (2)-es válasz nem lehet helyes.

Megjegyzés. Érdekes, hogy az a naiv érvelés, miszerint egy adott hőtágulási együtthatójú és hőkapacitású testre

W

is és

Q_{1}

is egyenesen arányos

Δ T

-vel (tehát

η

független a hőmérsékletkülönbségtől) hibás, mert sérti a második főtételt. Ez a hibás megoldás az I. Nemzetközi Fizikai Diákolimpián (1967, Varsó), majd később több példatárban is felbukkant, és csak 2015-ben mutatott rá két olasz fizikus, Giacomo De Palma és Mattia C. Sormani annak tarthatatlanságára.

13. Egy jó ábrát készítve ,,látszik'', hogy az (1) lehet a helyes válasz.

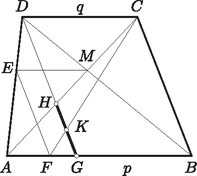
Jelöljük a

C F

és a

D G

egyenesek metszéspontját

K

-val, a trapéz átlóinak metszéspontját

M

-mel, továbbá legyen

A B = p

és

D C = q

, ahol

p > q

.
A

K G F

és

C B F

háromszögek hasonlók egymáshoz, úgyszintén a

H G A

C B A

háromszögek is. Ezek alapján

\begin{matrix} H G : K G = (\frac{A G}{A B} \cdot C B) : (\frac{F G}{F B} \cdot C B) = \frac{A G}{F G} : \frac{A B}{F B} . \end{matrix}

Mivel

A G D ▵ \sim A F E

A M E ▵ \sim A C D

és

A B M ▵ \sim C D M

, azért

\begin{matrix} \frac{A F}{F G} = \frac{A E}{E D} = \frac{A M}{M C} = \frac{A B}{D C} = \frac{p}{q} . \end{matrix}

A G = A F + F G = p - q

, ezért ebből

\begin{matrix} A F = \frac{p}{p + q} \cdot A G és F G = \frac{q}{p + q} \cdot A G, vagyis \frac{A G}{F G} = \frac{p + q}{q} . \end{matrix}

Másrészt

\begin{matrix} F B = F G + G B = \frac{q}{p + q} \cdot (p - q) + q = \frac{2 p q}{p + q}, amiből \frac{A B}{F B} = \frac{p + q}{2 q} . \end{matrix}

Tehát

H G : K G = \frac{A G}{F G} : \frac{A B}{F B} = 2

13 + 1

. A nulla nyugalmi tömegű neutrínók (sokáig ilyennek vélték ezeket a részecskéket) csak egyféle ,,csavarodási iránnyal'' rendelkeznek, vagy ,,jobbkezes'', vagy ,,balkezes'' állapotúak. A véges nyugalmi tömegű, feles spinű részecskék (ilyen például az elektron is) kétféle spinállapotban fordulhatnak elő (ezt fogalmazza meg a Pauli-elv). A legfrissebb (2015-ben fizikai Nobel-díjjal is elismert) mérési eredmények szerint a háromféle neutrínó közül legalább kettőnek nem nulla a nyugalmi tömege, tehát az összes lehetséges spinállapot

2 + 2 + 1 = 5

, de esetleg akár 6 is lehet.