Cím:	Megoldásvázlatok a 2015/9. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):	Katz Sándor
Füzet:	2016/január, 13 - 19. oldal	PDF  |  MathML

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. rész     1. Határozzuk meg a következő kifejezések pontos értékét közelítő értékek használata nélkül: ${\displaystyle \begin{array}{c}\hfill {\displaystyle a=\text{sin}{75}^{\circ }\cdot \text{cos}{75}^{\circ }\mathrm{,}b=\frac{5^{\text{lg}20}}{{20}^{1+\text{lg}5}}\mathrm{,}}\hfill \\ \hfill {\displaystyle c=\frac{1}{\sqrt[]{1}+\sqrt[]{2}}+\frac{1}{\sqrt[]{2}+\sqrt[]{3}}+\frac{1}{\sqrt[]{3}+\sqrt[]{4}}+\text{...}+\frac{1}{\sqrt[]{99}+\sqrt[]{100}}\mathrm{.}}\hfill \end{array}}$  ($\text{4}+\text{5}+\text{4}$ pont)   Megoldás. $a)$ $\text{sin}{75}^{\circ }\cdot \text{cos}{75}^{\circ }=\frac{1}{2}\cdot 2\text{sin}{75}^{\circ }\cdot \text{cos}{75}^{\circ }=\frac{1}{2}\cdot \text{sin}{150}^{\circ }=\frac{1}{2}\cdot \text{sin}{30}^{\circ }=\frac{1}{4}$. $b)$ I. megoldás. $\text{lg}b=\text{lg}20\cdot \text{lg}5-\left(1+\text{lg}5\right)\text{lg}20=\text{lg}1/20$. Az $f\left(x\right)=\text{lg}x$ függvény kölcsönösen egyértelmű, ezért $b=1/20$. II. megoldás. Használjuk fel, hogy ha $a$, $b$, $c$ pozitív és $b\ne$1, akkor $a^{\text{log}{}_{b}c}=c^{\text{log}{}_{b}a}$: $\begin{array}{c}{\displaystyle b=\frac{5^{\text{lg}20}}{{20}^{1+\text{lg}5}}=\frac{5^{\text{lg}20}}{20\cdot {20}^{\text{lg}5}}=\frac{1}{20}=0\mathrm{,}05.}\end{array}$ $c)$ Gyöktelenítsük a nevezőket: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle c}& {\displaystyle =\frac{1}{\sqrt[]{1}+\sqrt[]{2}}+\frac{1}{\sqrt[]{2}+\sqrt[]{3}}+\frac{1}{\sqrt[]{3}+\sqrt[]{4}}+\text{...}+\frac{1}{\sqrt[]{99}+\sqrt[]{100}}=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\frac{\sqrt[]{2}-\sqrt[]{1}}{2-1}+\frac{\sqrt[]{3}-\sqrt[]{2}}{3-2}+\frac{\sqrt[]{4}-\sqrt[]{3}}{4-3}+\text{...}+\frac{\sqrt[]{100}-\sqrt[]{99}}{100-99}=\sqrt[]{100}-\sqrt[]{1}=9.}\hfill \end{array}}$   2. Egy háromszögben két oldal hosszának különbsége $a-b=4\text{cm}$, a velük szemközti szögek $\alpha ={60}^{\circ }$, $\beta ={40}^{\circ }$. Mekkora a háromszög területe?  (12 pont)   I. megoldás. Szinusztétellel: $\begin{array}{c}{\displaystyle \frac{b+4}{b}=\frac{\text{sin}{60}^{\circ }}{\text{sin}{40}^{\circ }}\mathrm{.}}\end{array}$ Ebből $b\approx 11\mathrm{,}52$ cm, $a\approx 15\mathrm{,}52$ cm, $\begin{array}{c}{\displaystyle t=\frac{1}{2}ab\text{sin}{80}^{\circ }\approx 88\mathrm{,}04{\text{cm}}^2\mathrm{.}}\end{array}$ II. megoldás. Tangenstétellel: $\begin{array}{c}{\displaystyle \frac{a+b}{a-b}=\frac{\text{tg}\frac{\alpha +\beta }{2}}{\text{tg}\frac{\alpha -\beta }{2}}=\frac{\text{tg}{50}^{\circ }}{\text{tg}{10}^{\circ }}\mathrm{,}}\end{array}$ így $a+b=27\mathrm{,}04$ cm. Ebből $a=15\mathrm{,}52$ cm, $b=11\mathrm{,}52$ cm, $t=\frac{1}{2}ab\text{sin}{80}^{\circ }\approx 88\mathrm{,}04{\text{cm}}^2$. III. megoldás. Legyen $D$ a $BC$ oldalnak az a pontja, amelyre $DC=AC$. Ekkor $DB=4$ cm, és az $ADB$ háromszög szögei ${10}^{\circ }$, ${40}^{\circ }$, ${130}^{\circ }$. Az $AB$ oldal szinusztétellel: 17,65 cm. $\begin{array}{c}{\displaystyle t=c^2\text{sin}{60}^{\circ }\cdot \frac{\text{sin}{40}^{\circ }}{2\text{sin}{80}^{\circ }}\approx 88\mathrm{,}05{\text{cm}}^2\mathrm{.}}\end{array}$   3. Egy matematikai teszt megírásában egy középiskola $100$ tanulója vett részt, és az átlagpontszámuk $100$. Az alsóévesek száma $50\%$-kal több, mint a felsőéveseké, a felsőévesek átlagpontszáma pedig $50\%$-kal magasabb, mint az alsóéveseké. Mennyi a felsőévesek átlagpontszáma?  (13 pont)   I. megoldás. Ha az alsóévesek száma 50%-kal több, akkor $1\mathrm{,}5:1=60:40$ arányban kell a százat felbontani. Tehát az alsóévesek 60-an, a felsőévesek 40-en vannak. Az is világos, hogy ha ugyanannyiszor többen vannak az alsóévesek, mint ahányszor több a felsőévesek átlagpontszáma, akkor összesen ugyanannyi pontot érnek el, mindegyik $\left(100\cdot 100\right)/2=5000$ pontot. Ha ezt 40 felsőéves éri el, akkor átlagpontszámuk $5000/40=125$. Ellenőrzésképp megállapíthatjuk, hogy az alsóévesek átlagpontszáma $5000/60=250/3$. Valóban: $\begin{array}{c}{\displaystyle \frac{125}{\frac{250}{3}}=\frac{\frac{375}{3}}{\frac{250}{3}}=1\mathrm{,}5.}\end{array}$ II. megoldás. Ha a felsőévesek létszáma $x$, akkor az alsóéveseké $1\mathrm{,}5x$. Ha az alsóévesek átlagpontszáma $y$, akkor a felsőéveseké $1\mathrm{,}5y$. $\begin{array}{c}{\displaystyle x+1\mathrm{,}5x=\mathrm{100,}\frac{x\cdot 1\mathrm{,}5y+y\cdot 1\mathrm{,}5x}{100}=100.}\end{array}$ Az első egyenletből $x=40$. A másodikból pedig $y=10000/120=250/3\approx 83\mathrm{,}3$. A felsőévesek átlagpontszáma $1\mathrm{,}5y=125$. 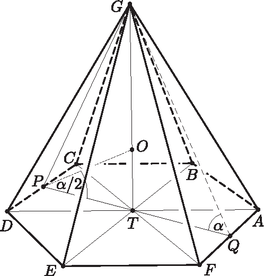Valóban: $\begin{array}{c}{\displaystyle \frac{40\cdot 125+\frac{250}{3}\cdot 60}{100}=100.}\end{array}$   4. Egy szabályos hatszög alapú gúla alapélei 5 cm, oldalélei 10 cm hosszúságúak. Mekkora a gúla térfogata, a beírt és köré írt gömb sugara? Mekkora egy oldallapnak az alaplappal bezárt szöge?  (13 pont)   Megoldás. A szabályos hatszög $AD$ átlója az oldal kétszerese: 10 cm. Így az $ADG$ háromszög szabályos, magassága: $TG=5\sqrt[]{3}$ cm.     Egy 5 cm oldalú szabályos háromszög területe: $\begin{array}{c}{\displaystyle t_1=\frac{25\sqrt[]{3}}{4}{\text{cm}}^2\mathrm{.}}\end{array}$ A gúla térfogata: $\begin{array}{c}{\displaystyle V=\frac{Tm}{3}=\frac{6\cdot 25\frac{\sqrt[]{3}}{4}\cdot 5\sqrt[]{3}}{3}=\frac{375}{2}{\text{cm}}^3\mathrm{.}}\end{array}$ Az $ADG$ háromszög köré írt kör sugara, egyben a gúla köré írt gömb sugara is: $\begin{array}{c}{\displaystyle R=\frac{2}{3}\cdot TG=\frac{10\sqrt[]{3}}{3}\approx 5\mathrm{,}774\text{cm. }}\end{array}$ Az oldallapnak az alaplappal bezárt szöge pl. a $TQG\sphericalangle =\alpha$, amelyre $\begin{array}{c}{\displaystyle \text{tg}\alpha =\frac{TG}{TQ}=\frac{5\sqrt[]{3}}{\frac{5\sqrt[]{3}}{2}}=\mathrm{2,}\text{amiből }\alpha =63\mathrm{,}{43}^{\circ }\mathrm{.}}\end{array}$ A beírt gömb sugara a $PQG$ háromszögbe írt kör sugarával egyenlő: $r=OT=PT\cdot \text{tg}\left(\alpha /2\right)\approx 2\mathrm{,}676$ cm.   II. rész     5. $a)$ Mennyi $\text{lg}x-\text{lg}y$ értéke, ha az $x$, $y$ számokra teljesül a $\begin{array}{c}{\displaystyle 2x^2-5xy+3y^2=0}\end{array}$ feltétel? $b)$ Oldjuk meg a valós számok halmazán a $4^{x+\frac{1}{2}}-5\cdot 6^x+9^{x+\frac{1}{2}}=0$ egyenletet. $c)$ Milyen $0\le \alpha <{360}^{\circ }$ szögek a megoldásai a $\begin{array}{c}{\displaystyle 4\text{sin}{}^2\alpha -5\text{sin}\alpha \cdot \text{cos}\alpha +5\text{cos}{}^2\alpha =2}\end{array}$ egyenletnek?  ($\text{5}+\text{5}+\text{6}$ pont)   Megoldás. $a)$ $\text{lg}x-\text{lg}y$ akkor értelmezhető, ha $x>0$ és $y>0$. Ez esetben a $2x^2-5xy+3y^2=0$ egyenletet eloszthatjuk $y^2$-tel: $\begin{array}{c}{\displaystyle 2\cdot {\left(\frac{x}{y}\right)}^2-5\cdot \frac{x}{y}+3=0.}\end{array}$ Az $\frac{x}{y}=t$ helyettesítéssel kapott $2t^2-5t+3=0$ egyenlet megoldásai $t_1=1$, $t_2=\frac{3}{2}$. Ha $\frac{x}{y}=$1, akkor $\text{lg}x-\text{lg}y=\text{lg}\frac{x}{y}=0$; ha $\frac{x}{y}=\frac{3}{2}$, akkor $\begin{array}{c}{\displaystyle \text{lg}x-\text{lg}y=\text{lg}\frac{x}{y}=\text{lg}\frac{3}{2}\approx 0\mathrm{,}1761.}\end{array}$ Azt használtuk fel, hogy az $a{x}^2+bxy+c{y}^2=0$ homogén másodfokú egyenletből meg tudjuk határozni $\frac{x}{y}$ értékét. Ezt fogjuk alkalmazni a $b)$ és $c)$ feladatokban is. ${\displaystyle \begin{array}{ccc}\hfill {\displaystyle 4^{x+\frac{1}{2}}-5\cdot 6^x+9^{x+\frac{1}{2}}}& {\displaystyle =\mathrm{0,}}\hfill & \text{(<mi>*</mi>)}\\ \hfill {\displaystyle 2\cdot 4^x-5\cdot 6^x+3\cdot 9^x}& {\displaystyle =0.}\hfill \end{array}}$ $9^x$ nem lehet 0, ezért oszthatjuk az egyenlet mindkét oldalát $9^x$-nel: $\begin{array}{c}{\displaystyle 2\cdot {\left(\frac{2}{3}\right)}^{2x}-5\cdot {\left(\frac{2}{3}\right)}^x+3=0.}\end{array}$ A ${\left(\frac{2}{3}\right)}^x=t$ helyettesítéssel kapott $2t^2-5t+3=0$ egyenlet megoldásai $t_1=1$, $t_2=\frac{3}{2}$. A ${\left(\frac{2}{3}\right)}^x=1$ egyenlet megoldása $x=0$, a ${\left(\frac{2}{3}\right)}^x=\frac{3}{2}$ egyenlet megoldása $x=-1$. $c)$ Ez esetben az egyenletünk nem homogén másodfokú, de ha a jobb oldalon álló 2 helyett $\left(2\text{sin}{}^2\alpha +2\text{cos}{}^2\alpha \right)$-t helyettesítünk, akkor 0-ra redukálva a $\begin{array}{c}{\displaystyle 2\text{sin}{}^2\alpha -5\text{sin}\alpha \cdot \text{cos}\alpha +3\text{cos}{}^2\alpha =0}\end{array}$ homogén egyenletet kapjuk. Az adott intervallumban $\alpha ={90}^{\circ }$ és $\alpha ={270}^{\circ }$ esetén lesz $\text{cos}\alpha =0$. Ezek egyike sem megoldása az egyenletnek, ezért oszthatjuk az egyenlet mindkét oldalát $\text{cos}{}^2\alpha$-val: $\begin{array}{c}{\displaystyle 2\text{tg}{}^2\alpha -5\text{tg}\alpha +3=0.}\end{array}$ A $\text{tg}\alpha =t$ helyettesítéssel kapott $2t^2-5t+3=0$ egyenlet megoldásai $t_1=1$, $t_2=\frac{3}{2}$. A $\text{tg}\alpha =1$ egyenlet megoldása az adott intervallumban $\alpha ={45}^{\circ }$ és $\alpha ={225}^{\circ }$. A $\text{tg}\alpha =\frac{3}{2}$ egyenlet megoldása az adott intervallumban $\alpha =56\mathrm{,}{31}^{\circ }$ és $\alpha =236\mathrm{,}{31}^{\circ }$. A $b)$ és $c)$ feladatban kapott gyökök is kielégítik az egyenleteket.   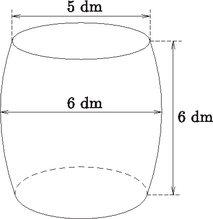6. Egy hordó legnagyobb átmérője 6 dm, legkisebb átmérője 5 dm, magassága 6 dm. (Ezek a hordó belső méretei.) A hordó olyan forgástestnek tekinthető, amely egy szimmetrikus parabolaív forgatásával keletkezett.     $a)$ Mekkora a hordó térfogata? $b)$ Hány százalékos hibát vétünk, ha a hordó térfogatát olyan hengerrel közelítjük, amelynek magassága megegyezik a hordóéval, átmérője pedig a hordó legkisebb és legnagyobb átmérőjének számtani közepével?  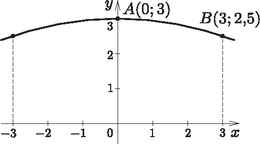(16 pont)   Megoldás. Helyezzük el a parabolaívet koordináta-rendszerbe, és határozzuk meg a parabola egyenletét.     Az $y$-tengelyre szimmetrikus parabola egyenlete $y=a{x}^2+b$. Az $A\left(0;3\right)$ és $B\left(3;2\mathrm{,}5\right)$ pontok illeszkednek a parabolára, ezért a koordináták kielégítik az egyenletet: $3=a\cdot 0+b$, illetve $2\mathrm{,}5=9a+b$. Ebből $a=-\frac{1}{18}$, $b=3$, azaz a parabola egyenlete $\begin{array}{c}{\displaystyle y=-\frac{1}{18}{x}^2+3.}\end{array}$ A forgástest térfogata ${\displaystyle \begin{array}{cc}\hfill {\displaystyle V}& {\displaystyle =\pi \underset{-3}{\overset{3}{\int }}{\left(-\frac{1}{18}{x}^2+3\right)}^{2}dx=\pi \underset{-3}{\overset{3}{\int }}\left(\frac{1}{324}{x}^4-\frac{1}{3}{x}^2+9\right)dx=}\hfill \\ \hfill {\displaystyle }& {\displaystyle =\pi {\left[\frac{x^5}{1620}-\frac{x^3}{9}+9x\right]}_{-3}^3\approx 151\mathrm{,}74{\text{dm}}^3\mathrm{.}}\hfill \end{array}}$ A közelítő henger térfogata $\begin{array}{c}{\displaystyle V_h={\left(\frac{2\mathrm{,}5+3}{2}\right)}^2\cdot 6\pi \approx 142\mathrm{,}55{\text{dm}}^3\mathrm{.}}\end{array}$ A közelítés abszolút hibája 9,19 dm, a relatív hiba $9\mathrm{,}19/151\mathrm{,}74=0\mathrm{,}0606$. Azaz a közelítés hibája 6,06%-os.   7. $a)$ Hányféleképpen állítható elő a $2016$ szomszédos pozitív egész számok összegeként? $b)$ Adjunk meg egy olyan, $2016$-nál nagyobb, pozitív egész számot, amely nem állítható elő szomszédos pozitív egész számok összegeként.  (16 pont)   Megoldás. $a)$ Legyen az első szám $n$, és adjunk össze $k\left(>1\right)$ db természetes számot, azaz $\begin{array}{c}{\displaystyle n+\left(n+1\right)+\left(n+2\right)+\text{...}+\left(n+k-1\right)=2016.}\end{array}$ Ezek a számok egy $k$ elemű számtani sorozatot alkotnak, ezért ${\displaystyle \begin{array}{cc}\hfill {\displaystyle S=\frac{k\cdot \left(n+\left(n+k-1\right)\right)}{2}}& {\displaystyle =\mathrm{2016,}}\hfill \\ \hfill {\displaystyle k\cdot \left(2n+k-1\right)}& {\displaystyle =\mathrm{4032,}}\hfill \\ \hfill {\displaystyle k\cdot \left(2n+k-1\right)}& {\displaystyle =2^6\cdot 3^2\cdot 7.}\hfill \end{array}}$ A $4032=2^6\cdot 3^2\cdot 7$ számnak $\left(6+1\right)\left(2+1\right)\left(1+1\right)=42$ pozitív osztója van. Ebből 21 pár készíthető, de ezek nem mind adnak $n$-re és $k$-ra pozitív egészeket. Ha figyelembe vesszük, hogy $k$ és 2$n+k-1$ különböző paritású, és a $2n+k-1>k>1$ feltételeket, akkor láthatjuk, hogy 4032-t úgy kell két, 1-nél nagyobb szám szorzatára bontani, hogy az egyik tényező páratlan, a másik páros legyen. Ekkor a kisebb tényező adja $k$ értékét, a nagyobb lesz $2n+k-1$. 4032-nek ugyanannyi páratlan osztója van, mint a $3^2\cdot 7=63$ számnak: $\left(2+1\right)\cdot \left(1+1\right)=6$ db. Ezek közül az 1-hez nem tartozik megfelelő $k$ és $n$. Tehát ötféle felbontás van, ezért 2016 ötféleképp írható fel szomszédos pozitív egész számok összegeként. (A megfelelő párok: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{|cccccc|}\hline \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>k</mi></math>}}\hfill & \hfill {\displaystyle \text{3}}\hfill & \hfill {\displaystyle \text{ 7}}\hfill & \hfill {\displaystyle \text{ 9}}\hfill & \hfill {\displaystyle \text{ 21}}\hfill & \hfill {\displaystyle \text{63 }}\hfill \\ \hfill {\displaystyle \text{2<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi><mo stretchy="false">+</mo><mi>k</mi></math>-1}}\hfill & \hfill {\displaystyle \text{1344}}\hfill & \hfill {\displaystyle \text{ 576}}\hfill & \hfill {\displaystyle \text{ 448}}\hfill & \hfill {\displaystyle \text{ 192}}\hfill & \hfill {\displaystyle \text{64 }}\hfill \\ \hfill {\displaystyle \text{<math xmlns="http://www.w3.org/1998/Math/MathML"><mi>n</mi></math>}}\hfill & \hfill {\displaystyle \text{671}}\hfill & \hfill {\displaystyle \text{ 285}}\hfill & \hfill {\displaystyle \text{ 220}}\hfill & \hfill {\displaystyle \text{ 86}}\hfill & \hfill {\displaystyle \text{1 }}\hfill \\ \hline\end{array}}}\end{array}$ A megfelelő összegek: $671+672+673$, $285+286+\text{...}+291$, $220+221+\text{...}+228$, $86+87+\text{...}+106$, $1+2+3+\text{...}+63$.) $b)$ A fenti megoldásból látható, hogy ha az $M$ számot akarjuk felírni szomszédos pozitív egész számok összegeként, akkor $2M$-et kell egy páros és egy 1-nél nagyobb páratlan szám szorzataként felírni. Ha $M$ kettő-hatvány, akkor $2M$-nek nincs 1-nél nagyobb páratlan osztója. Eszerint pl. $2^{11}=2048$ nem írható fel szomszédos pozitív egész számok összegeként.   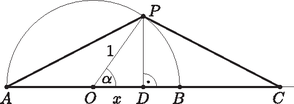8. Az $AB$ átmérőjű kör egy pontja $P$. Az $AB$ egyenesnek $C$ az a pontja, amelyre $AP=PC$. $P$ mely helyzetében lesz az $ACP$ háromszög területe maximális?  (16 pont)   I. megoldás. Legyen a kör sugara 1, a $P$ pontból az $AC$-re állított merőleges talppontja $D$ és legyen $OD=x$.     Ekkor $PD=\sqrt[]{1-x^2}$. $\begin{array}{c}{\displaystyle T_{APC}=\frac{AC\cdot PD}{2}=\frac{2\cdot \left(1+x\right)\sqrt[]{1-x^2}}{2}\mathrm{.}}\end{array}$ Mivel $T$ pozitív, ezért ugyanott van maximuma, mint négyzetének. $T^2$-re alkalmazhatjuk a számtani és mértani közép összefüggését négy számra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{APC}^2}& {\displaystyle ={\left(1+x\right)}^2\left(1-x^2\right)=\frac{1}{3}{\left(1+x\right)}^3\left(3-3x\right)\le }\hfill \\ \hfill {\displaystyle }& {\displaystyle \le \frac{1}{3}\cdot {\left(\frac{\left(1+x\right)+\left(1+x\right)+\left(1+x\right)+\left(3-3x\right)}{4}\right)}^4=\frac{1}{3}{\left(\frac{6}{4}\right)}^4\mathrm{.}}\hfill \end{array}}$ Ebből: $\begin{array}{c}{\displaystyle T_{APC}\le \frac{1}{\sqrt[]{3}}\frac{9}{4}=\frac{3\sqrt[]{3}}{4}\mathrm{.}}\end{array}$ $T_{APC}$ ezt a maximális értéket akkor veszi fel, ha $1+x=3-3x$, azaz $x=0\mathrm{,}5$.   II. megoldás. Legyen a kör sugara 1, és legyen $POD=\alpha$ ($0^{\circ }<\alpha <{90}^{\circ }$). Ekkor $PD=\text{sin}\alpha$, $OD=\text{cos}\alpha$. $\begin{array}{c}{\displaystyle T_{APC}=\frac{AC\cdot PD}{2}=\frac{2\cdot \left(1+\text{cos}\alpha \right)\text{sin}\alpha }{2}=\left(1+\text{cos}\alpha \right)\text{sin}\alpha \mathrm{.}}\end{array}$ Ezt négyzetre emelve újra alkalmazhatjuk a számtani és mértani közép összefüggését négy számra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle T_{APC}^2}& {\displaystyle ={\left(1+\text{cos}\alpha \right)}^2\text{sin}{}^2\alpha ={\left(1+\text{cos}\alpha \right)}^3\left(1-\text{cos}\alpha \right)=\frac{1}{3}{\left(1+\text{cos}\alpha \right)}^3\left(3-3\text{cos}\alpha \right)\le }\hfill \\ \hfill {\displaystyle }& {\displaystyle \le \frac{1}{3}\cdot {\left(\frac{3\left(1+\text{cos}\alpha \right)+\left(3-3\text{cos}\alpha \right)}{4}\right)}^4=\frac{1}{3}{\left(\frac{6}{4}\right)}^4\mathrm{.}}\hfill \end{array}}$ Ebből: $\begin{array}{c}{\displaystyle T_{APC}\le \frac{1}{\sqrt[]{3}}\frac{9}{4}=\frac{3\sqrt[]{3}}{4}\mathrm{.}}\end{array}$ $T_{APC}$ ezt az értéket akkor veszi fel, ha $1+\text{cos}\alpha =3-3\text{cos}\alpha$, azaz $\text{cos}\alpha =0\mathrm{,}5$, $\alpha ={60}^{\circ }$.   III. megoldás. A $T_{APC}=\left(1+\text{cos}\alpha \right)\text{sin}\alpha =\text{sin}\alpha +0\mathrm{,}5\cdot \text{sin}2\alpha$ függvény maximumát differenciálással keressük meg: $\begin{array}{c}{\displaystyle T\text{'}=\text{cos}\alpha +\text{cos}2\alpha =\text{cos}\alpha +2\text{cos}{}^2\alpha -1.}\end{array}$ Ennek zérushelyei $\text{cos}\alpha =0\mathrm{,}5$ és $\text{cos}\alpha =-1$. A feladatnak csak az első felel meg, és táblázattal, vagy második deriválttal beláthatjuk, hogy $\alpha ={60}^{\circ }$-nál a területnek valóban maximuma van.   9. Ha felírjuk az összes olyan ötjegyű számot, amelyben az $1$ és $2$ számjegyeken kívül más jegy nem szerepel, akkor mennyi lesz $a)$ a felírt számok összege, $b)$ a felírt számjegyek összege, $c)$ annak a valószínűsége, hogy két véletlenszerűen kiválasztott ilyen számban ugyanannyi a számjegyek összege?  ($\text{5}+\text{4}+\text{7}$ pont)   Megoldás. $2^5=32$ ilyen szám van. Minden helyiértéken a számjegyek fele 1-es, a fele 2-es, tehát a számok összege $\begin{array}{c}{\displaystyle \left(1+10+100+1000+10000\right)\left(16\cdot 1+16\cdot 2\right)=533328.}\end{array}$ Megjegyzés. Az 11111, 11112, 11121, $\text{...}$, 22212, 22221, 22222 nem számtani sorozat, de a számtani sorozatra jellemző $\begin{array}{c}{\displaystyle S=\frac{32\cdot \left(11111+22222\right)}{2}}\end{array}$ képlet helyes végeredményt ad. Ennek az oka, hogy a sorozatban a $k$-adik és $\left(33-k\right)$-adik elem összege mindig 33 333. $b)$ Az $5\cdot 32=160$ jegy fele 1-es a fele 2-es, tehát a számjegyek összege $80\cdot \left(1+2\right)=240$. $c)$ Az adott számokban a jegyek összege 5, 6, 7, 8, 9 és 10 lehet, de 5 és 10 csak egy-egy számban lesz az összeg, vagyis nem lehet két kiválasztott számban a jegyek összege 5, illetve 10. A jegyek összege annyi számban lesz 6, 7, 8 vagy 9, ahányféleképp az öt helyen el tudjuk osztani az 1, 2, 3 vagy 4 db 2-es számjegyet. 5 számban lesz a jegyek összege 6, 10-ben 7, 10-ben 8, és 5-ben 9. Ezek páronként kizáró lehetőségek, ezért annak a valószínűsége, hogy két választott számban a jegyek összege egyenlő: $\begin{array}{c}{\displaystyle \frac{\left(\genfrac{}{}{0ex}{}{5}{2}\right)}{\left(\genfrac{}{}{0ex}{}{32}{2}\right)}+\frac{\left(\genfrac{}{}{0ex}{}{10}{2}\right)}{\left(\genfrac{}{}{0ex}{}{32}{2}\right)}+\frac{\left(\genfrac{}{}{0ex}{}{10}{2}\right)}{\left(\genfrac{}{}{0ex}{}{32}{2}\right)}+\frac{\left(\genfrac{}{}{0ex}{}{5}{2}\right)}{\left(\genfrac{}{}{0ex}{}{32}{2}\right)}=\frac{110}{496}=\frac{55}{248}\approx 0\mathrm{,}2218.}\end{array}$