Cikkünkben egy egyszerű fizikai elv segítségével ellenállás-hálózatokból nyerhető egyenlőtlenségekkel foglalkozunk. Az első részben ‐ amely a KöMaL 2015. decemberi számának 514.‐524. oldalán olvasható ‐ a Milne-egyenlőtlenséggel ismerkedtünk meg. Most a Minkowski-egyenlőtlenség egy speciális esetével folytatjuk. Az egyenletek, ábrák stb. számozása folytatólagos.

 

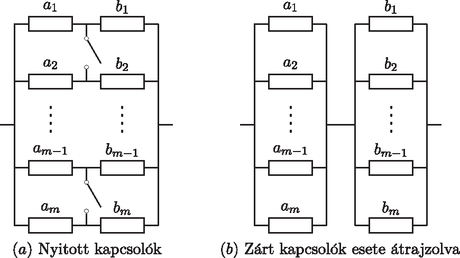8. ábra A (6.7) egyenlőtlenség hálózatai

 

6.2. feladat. Mutassuk meg (a bizonyítás végigkövetésével), hogy a (6.7) egyenlőtlenségben pontosan akkor teljesül az egyenlőség, ha az $\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_m\right)$, $\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_m\right)$ vektorok azonos irányúak.

 

A korábban már bevezetett szummás jelölésmóddal a (6.7) egyenlőtlenség a következőképpen írható:

$\begin{array}{c}{\displaystyle {\left(\sum _{i=1}^m{\left(a_i+b_i\right)}^{-1}\right)}^{-1}\ge {\left(\sum _{i=1}^m{a}_i^{-1}\right)}^{-1}+{\left(\sum _{i=1}^m{b}_i^{-1}\right)}^{-1}\mathrm{.}}\end{array}$

Ez az alak valójában speciális esete egy sokkal általánosabb egyenlőtlenségcsaládnak, amelyben a $\left(-1\right)$ kitevő helyett tetszőleges valós $p\ne 0$ kitevő szerepel: ha $p\ge 1$ és $x_i$, $y_i$ $\left(i=\mathrm{1,}\text{...}\mathrm{,}m\right)$ tetszőleges valós számok, akkor

$\begin{array}{c}{\displaystyle {\left(\sum _{i=1}^m{|x_i+y_i|}^p\right)}^{1/p}\le {\left(\sum _{i=1}^m{|x_i|}^p\right)}^{1/p}+{\left(\sum _{i=1}^m{|y_i|}^p\right)}^{1/p}\mathrm{,}}\end{array}$

(6.9)

ha pedig $p<1$, $p\ne 0$ és az $x_i$, $y_i$ számok mind pozitívak, akkor fordított egyenlőtlenség teljesül. Ezt az egyenlőtlenségcsaládot, legalábbis a $p\ge 1$ esetét az irodalomban Minkowski-egyenlőtlenség néven szokás hívni (a $p<1$ esetet inkább fordított Minkowski-egyenlőtlenségnek). Hermann Minkowski (1864‐1909) német matematikus ‐ aki ugyancsak a Königsbergi Egyetemen tanult ‐ 1896-ban igazolta az egyenlőtlenséget geometriai vizsgálódásai során (lásd a [3] könyv 115‐117. oldalait). A $p=2$ speciális esetben

$\begin{array}{c}{\displaystyle {\left(\sum _{i=1}^m{|x_i|}^p\right)}^{1/p}=\sqrt[]{x_1^2+\text{...}+x_m^2}}\end{array}$

éppen az $\text{x}=\left(x_1\mathrm{,}\text{...}\mathrm{,}{x}_m\right)$ $m$-dimenziós vektor euklidészi hossza (gondoljunk az $m=\mathrm{2,3}$ speciális esetekre), amelyre bevezetve az $|\text{x}|$ jelölést, a Minkowski-egyenlőtlenség az

$\begin{array}{c}{\displaystyle |\text{x}+\text{y}|\le |\text{x}|+|\text{y}|}\end{array}$

tömör alakba írható át. Ez az úgynevezett $m$-dimenziós háromszög-egyenlőtlenség, amelyet kétdimenzióban bizonyára mindenki jól ismer és a 9. ábra szemléltet: tetszőleges ‐ akár elfajuló ‐ háromszögben bármely két oldal hosszának összege legalább akkora, mint a harmadik oldal hossza (mi köze ennek a 4.5. feladat négyzetes középre vonatkozó részéhez?). A 9. ábráról az is világos, hogy egyenlőség csak akkor van, ha az $\text{x}$ és $\text{y}$ vektorok azonos irányúak.

 

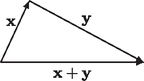9. ábra. Háromszög-egyenlőtlenség

 

A $p\ge 1$ esetben az

$\begin{array}{c}{\displaystyle {|\text{x}|}_p:={\left(\sum _{i=1}^m{|x_i|}^p\right)}^{1/p}}\end{array}$

képlettel az euklidészi hosszúság fogalmának egy általánosítása, úgynevezett norma értelmezhető ‐ vajon mit ad ${|\text{x}|}_p$, ha $p\to \infty$? ‐, amelyre nézve a Minkowski-egyenlőtlenség éppen a háromszög-egyenlőtlenség:

$\begin{array}{c}{\displaystyle {|\text{x}+\text{y}|}_p\le {|\text{x}|}_p+{|\text{y}|}_p\mathrm{.}}\end{array}$

A Minkowski-egyenlőtlenségnek egy másik interpretációját adják a hatványközepek. Az $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_m$ pozitív valós számok $p$-edik hatványközepe (ahol $p$ tetszőleges nem nulla valós szám)

$\begin{array}{c}{\displaystyle M_p\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_m\right)={\left(\frac{a_1^p+a_2^p+\text{...}+a_m^p}{m}\right)}^{1/p}\mathrm{.}}\end{array}$

(6.10)

Speciálisan $p=1$ esetén

$\begin{array}{c}{\displaystyle M_1\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_m\right)=\frac{a_1+a_2+\text{...}+a_m}{m}\mathrm{,}}\end{array}$

a számtani, $p=2$ esetén

$\begin{array}{c}{\displaystyle M_2\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_m\right)=\sqrt[]{\frac{a_1^2+a_2^2+\text{...}+a_m^2}{m}}}\end{array}$

a négyzetes közép, továbbá $p=-1$ esetén

$\begin{array}{c}{\displaystyle M_{-1}\left(a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_m\right)=\frac{m}{\frac{1}{a_1}+\frac{1}{a_2}+\text{...}+\frac{1}{a_m}}}\end{array}$

a már korábban (lásd a (6.1) formulát) $H_m$-mel jelölt harmonikus közép. Sőt némi analízis segítségével (lásd a [5] könyv 248‐250. oldalait) belátható az is, hogy $M_p$ formulája folytonosan kiterjeszthető a $p=0$ értékre is, mégpedig

$\begin{array}{c}{\displaystyle M_0\left(a_1\mathrm{,}{a}_2\text{...}\mathrm{,}{a}_m\right)=\sqrt[m]{a_1\cdot a_2\cdot \text{...}\cdot a_m}}\end{array}$

a geometriai közép. Ekkor a (6.9) Minkowski-egyenlőtlenséget és a fordítottját $m^{1/p}$-nel osztva, pozitív $x_i=a_i$, $y_i=b_i$ $\left(i=\mathrm{1,}\text{...}\mathrm{,}m\right)$ számok választásával éppen azt kapjuk, hogy $p\ge 1$ esetén

$\begin{array}{c}{\displaystyle M_p\left(a_1+b_1\mathrm{,}\text{...}\mathrm{,}{a}_m+b_m\right)\le M_p\left(a_1\mathrm{,}\text{...}\mathrm{,}{a}_m\right)+M_p\left(b_1\mathrm{,}\text{...}\mathrm{,}{b}_m\right);}\end{array}$

ha pedig $p<1$ (a $p=0$ esetet is beleértve), akkor fordított egyenlőtlenség érvényes. Mindez a (6.8) egyenlőtlenség általánosítása a hatványközepekre (amely a 4.5. feladat kérdéseire is választ ad).
A Minkowski-egyenlőtlenség általános esetével kapcsolatban további olvasmányként a [9] cikket ajánljuk, amely a konvexitás fogalmának segítségével közös kiindulópontra vezeti vissza a Minkowski-, a Milne- és még más nevezetes egyenlőtlenségeket, valamint a Milne-egyenlőtlenség egy általánosítását is megfogalmazza.

 

6.3. megjegyzés. Megmutatható, hogy ha Ohm törvénye helyett a nemlineáris

$\begin{array}{c}{\displaystyle U=R\cdot I^{-1/p}}\end{array}$

összefüggés lenne érvényes az ellenállásokra (ahol $p=-1$ felel meg Ohm törvényének), akkor az eddigiekben tárgyalt megfontolások általánosításaként éppen a Minkowski-egyenlőtlenséget nyerjük. Erről kicsit bővebben olvashatunk a [7] cikkben.

 

7. Számtani és harmonikus közép újra

Elérkeztünk cikkünk legáltalánosabb ellenállás-hálózatához, ezt mutatja a 10. ábra. Az összes kapcsoló nyitott, majd zárt állapotában felírva az eredő ellenállást, és ezután kihasználva Rayleigh monotonitási törvényét, az előző szakaszok hálózatainak mintájára könnyen látható, hogy az alábbi egyenlőtlenséghez jutunk.

 

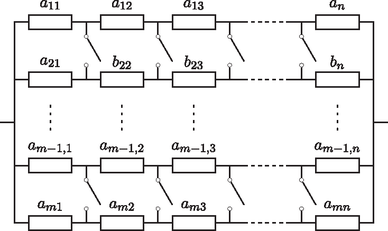10. ábra. A (7.1) egyenlőtlenség hálózata

 

 

7.1. állítás. Ha $a_{ij}$, $b_{ij}$ $(i=\mathrm{1,}\text{...}\mathrm{,}m;$ $j=\mathrm{1,}\text{...}\mathrm{,}n)$ pozitív számok, akkor

$\begin{array}{c}{\displaystyle {\left(\sum _{i=1}^m{\left(\sum _{j=1}^n{a}_{ij}\right)}^{-1}\right)}^{-1}\ge \sum _{j=1}^n{\left(\sum _{i=1}^m{a}_{ij}^{-1}\right)}^{-1}\mathrm{,}}\end{array}$

(7.1)

vagy ekvivalensen
${\displaystyle \begin{array}{c}\hfill {\displaystyle H_m\left(a_{11}+\text{...}+a_{1n}\mathrm{,}{a}_{21}+\text{...}+a_{2n}\mathrm{,}\text{...}\mathrm{,}{a}_{m1}+\text{...}+a_{mn}\right)\ge }\hfill \\ \hfill {\displaystyle \ge H_m\left(a_{11}\mathrm{,}\text{...}\mathrm{,}{a}_{m1}\right)+H_m\left(a_{12}\mathrm{,}\text{...}\mathrm{,}{a}_{m2}\right)+\text{...}+H_m\left(a_{1n}\mathrm{,}\text{...}\mathrm{,}{a}_{mn}\right)\mathrm{.}}\hfill \end{array}}$


Speciálisan $n=2$ esetén éppen a már igazolt (6.7) egyenlőtlenséget kapjuk, és ebből kiindulva az 5.1. állítás bizonyításának mintájára $n$-re vonatkozó teljes indukcióval rögtön adódik az általános eset.

 

7.2. feladat. Gondoljuk végig a 7.1. állítás bizonyítását $n$-re vonatkozó teljes indukcióval, és mutassuk meg, hogy egyenlőség csakis akkor teljesül, ha az $\left(a_{1j}\mathrm{,}\text{...}\mathrm{,}{a}_{mj}\right)$ $\left(j=\mathrm{1,}\text{...}\mathrm{,}n\right)$ vektorok páronként azonos irányúak.

 

Természetesen az $n$-re vonatkozó teljes indukció helyett $m$-re vonatkozó indukciót is használhatunk az $m=2$ esetből (vagyis az 5.1. állításból) kiindulva úgy, ahogyan a (6.7) egyenlőtlenséget is igazoltuk.

 

7.3. feladat. Gondoljuk végig a 7.1. állítás bizonyítását $m$-re vonatkozó teljes indukcióval, és mutassuk meg, hogy egyenlőség pontosan akkor teljesül, ha az $\left(a_{i1}\mathrm{,}\text{...}\mathrm{,}{a}_{in}\right)$ $\left(i=\mathrm{1,}\text{...}\mathrm{,}m\right)$ vektorok páronként azonos irányúak.

 

A jobb átláthatóság érdekében gyakran célszerű az $a_{ij}$ $(i=\mathrm{1,}\text{...}\mathrm{,}m$; $j=\mathrm{1,}\text{...}\mathrm{,}n)$ számokat egy $m\times n$-es táblázatba, matematikai nyelven $m\times n$-es mátrixba rendezni:

$\begin{array}{c}{\displaystyle A=\left({\displaystyle \begin{array}{cccc}\hfill {\displaystyle a_{11}}\hfill & \hfill {\displaystyle a_{12}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{1n}}\hfill \\ \hfill {\displaystyle a_{21}}\hfill & \hfill {\displaystyle a_{22}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{2n}}\hfill \\ \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle \ddots }\hfill & \hfill {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle a_{m1}}\hfill & \hfill {\displaystyle a_{m2}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{mn}}\hfill \end{array}}\right)}\end{array}$

Az egyenlőség a 7.2. és 7.3. feladatokban megfogalmazott feltételeiből következően a mátrixra az alábbi kis állítást nyertük.

 

7.4. állítás. Az $A$ mátrix oszlopaiból képzett $m$-dimenziós vektorok pontosan akkor azonos irányúak, amikor a sorokból képzett $n$-dimenziós vektorok azonos irányúak.

 

7.5. feladat. Igazoljuk közvetlenül (a 7.2. és 7.3. feladatok felhasználása nélkül) a 7.4. állítást.

 

Térjünk még vissza a (7.1) egyenlőtlenségre néhány gondolat erejéig. Először is érdemes végiggondolni, hogy milyen egyenlőtlenségeket kapunk, ha a 10. ábra hálózatában nem az összes kapcsolót zárjuk.

 

7.6. feladat. Írjuk fel, hogy milyen egyenlőtlenségek adódnak a Rayleigh-féle monotonitási elvből, ha a 10. ábra hálózatában csak bizonyos sorok vagy oszlopok kapcsolóit zárjuk.

 

A (7.1) egyenlőtlenségnek egy speciális esete is figyelemre méltó. Tekintsük ugyanis az

$\begin{array}{c}{\displaystyle \left({\displaystyle \begin{array}{cccc}\hfill {\displaystyle a_{11}}\hfill & \hfill {\displaystyle a_{12}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{1n}}\hfill \\ \hfill {\displaystyle a_{21}}\hfill & \hfill {\displaystyle a_{22}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{2n}}\hfill \\ \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle \ddots }\hfill & \hfill {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle a_{n1}}\hfill & \hfill {\displaystyle a_{n2}}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{nn}}\hfill \end{array}}\right)=\left({\displaystyle \begin{array}{cccc}\hfill {\displaystyle a_1}\hfill & \hfill {\displaystyle a_2}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_n}\hfill \\ \hfill {\displaystyle a_2}\hfill & \hfill {\displaystyle a_3}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_1}\hfill \\ \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle ⋮}\hfill & \hfill {\displaystyle \ddots }\hfill & \hfill {\displaystyle ⋮}\hfill \\ \hfill {\displaystyle a_n}\hfill & \hfill {\displaystyle a_1}\hfill & \hfill {\displaystyle \cdots }\hfill & \hfill {\displaystyle a_{n-1}}\hfill \end{array}}\right)}\end{array}$

szereposztást, ahol a jobb oldali mátrix egy sorát ,,eggyel balra tolva és a legutolsó elemet előre helyezve'' kaptuk a rákövetkező sort. Könnyen látható, hogy ekkor a (7.1) egyenlőtlenség az alábbi alakra egyszerűsödik:

$\begin{array}{c}{\displaystyle \frac{a_1+\text{...}+a_n}{n}\ge \frac{n}{\frac{1}{a_1}+\text{...}+\frac{1}{a_n}}\mathrm{,}}\end{array}$

(7.2)

ami éppen az $a_1\mathrm{,}\text{...}\mathrm{,}{a}_n$ számok számtani és harmonikus közepei közötti egyenlőtlenség.

 

7.7. feladat. Bizonyítsuk be (a (7.1) egyenlőtlenségbeli egyenlőség feltételének ismeretében), hogy a (7.2) egyenlőtlenségben pontosan akkor áll fenn egyenlőség, ha $a_1=a_2=\text{...}=a_n$.

 

A két pozitív szám számtani és harmonikus közepei között érvényes (3.2) azonosság valójában $n$ pozitív szám esetére is általánosítható, és ezzel egy újabb bizonyítást nyerünk a (7.2) egyenlőtlenségre.

 

7.8. feladat. Alakítsuk négyzetösszeggé az

$\begin{array}{c}{\displaystyle \frac{a_1+\text{...}+a_n}{n}-\frac{n}{\frac{1}{a_1}+\text{...}+\frac{1}{a_n}}}\end{array}$

kifejezést. Segítség: $n=3$ esetén

$\begin{array}{c}{\displaystyle \frac{a_1+a_2+a_3}{3}-\frac{3}{\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}}=\frac{{\left(a_1-a_2\right)}^2{a}_3+{\left(a_2-a_3\right)}^2{a}_1+{\left(a_1-a_3\right)}^2{a}_2}{3\left(a_1{a}_2+a_2{a}_3+a_1{a}_3\right)}\mathrm{.}}\end{array}$

 

7.9. megjegyzés. A (6.7) egyenlőtlenséghez hasonlóan a (7.1) egyenlőtlenség is valójában egy általánosabb család tagja: ha $p\ge 1$ és $x_{ij}$ $(i=\mathrm{1,}\text{...}\mathrm{,}m$; $j=\mathrm{1,}\text{...}\mathrm{,}n)$ tetszőleges valós számok, akkor

$\begin{array}{c}{\displaystyle {\left(\sum _{i=1}^m|\sum _{j=1}^n{x}_{ij}{|}^p\right)}^{1/p}\le \sum _{j=1}^n{\left(\sum _{i=1}^m{|x_{ij}|}^p\right)}^{1/p}\mathrm{,}}\end{array}$

(7.3)

ha pedig $p<1$, $p\ne 0$ és az $x_{ij}$ számok mind pozitívak, akkor fordított az egyenlőtlenség iránya. A $p=2$ eset nem más, mint az $m$-dimenziós háromszög-egyenlőtlenségnek a ,,töröttvonal-egyenlőtlenség'' változata, mely szerint egy zárt töröttvonal bármely oldalának hossza legfeljebb akkora, mint a többi oldal hosszának összege. Valóban, az ${\text{x}}_j=\left(x_{1j}\mathrm{,}\text{...}\mathrm{,}{x}_{mj}\right)$ $\left(j=\mathrm{1,}\text{...}\mathrm{,}n\right)$ vektorok bevezetésével arról van szó, hogy

$\begin{array}{c}{\displaystyle |{\text{x}}_1+\text{...}+{\text{x}}_n|\le |{\text{x}}_1|+\text{...}+|{\text{x}}_n|\mathrm{,}}\end{array}$

amit a 11. ábra szemléltet. Erről az egyenlőség feltétele is szemléletes, az ${\text{x}}_1\mathrm{,}\text{...}\mathrm{,}{\text{x}}_n$ vektoroknak páronként azonos irányúaknak kell lenniük.

 

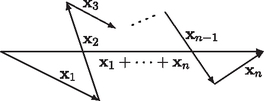11. ábra. Háromszög-egyenlőtlenség általánosítása

 

 

7.10. feladat. Fogalmazzuk meg a (7.3) egyenlőtlenséget (a (6.10) képlettel értelmezett) hatványközepek segítségével.

 

7.11. történeti megjegyzés. A (7.1) egyenlőtlenségnek a 10. ábra ellenállás-hálózatához való szoros kapcsolatát először Alfred Lehman (1931‐2006) vette észre, aki 1960-ban a SIAM Review folyóirat feladatrovatában ‐ amelynek egyébként Murray S. Klamkin (1921‐2004), amerikai matematikus és rendkívül termékeny feladatkitűző volt a szerkesztője ‐ írta le az ötletet, és tűzte ki feladatként a precíz bizonyítást (lásd [1]). Lehman kapcsolók nyitása és zárása helyett egyszerűen rövidre zárta az ellenállásokat, de talán a kapcsolók beiktatása természetesebb gondolat, ezért érveltünk mi így. A kitűzött feladatra beérkezett megoldások közül a rovatban két évvel később Fazlollah Reza ‐ idén 101 éves ‐ perzsa matematikus megoldását jelentették meg, amely éppen az általunk is tárgyalt teljes indukciós bizonyítás. Emellett Lehman megjegyzéseit is közölték, amelyben felhívja a figyelmet a Minkowski-egyenlőtlenséggel való rokonságra, valamint a 6.3. megjegyzés végén említett nemlineáris Ohm-törvénnyel kapcsolatos általánosítási lehetőségekre. Mindezek miatt gyakran a különböző cikkekben Lehman-egyenlőtlenségként emlegetik a (4.2) egyenlőtlenséget, miközben azt Milne már jóval korábban és általánosabb formában használta.

 

Bár cikkünk lassan a végéhez közeledik, de az általánosítások sora korántsem ér véget. A tárgyalt ellenállások helyett ugyanis több be- és kimenettel rendelkező (többpólusú) ellenállásokat is egymáshoz kapcsolhatunk. Ekkor az ellenállásokat egyetlen szám helyett egy mátrixszal írhatjuk le. Soros kapcsolás esetén az eredő ellenállást a mátrixok (elemenként vett) összege adja meg, párhuzamos kapcsolás esetén az (1.3) összefüggés megfelelő általánosítása lesz érvényben és mátrixok úgynevezett parallel összegét kapjuk. Ennek segítségével lehet például értelmezni két mátrix harmonikus közepét. Éppen ez motiválta és indította el a mátrixok, majd még általánosabb objektumok ‐ úgynevezett operátorok ‐ közepei elméletének fejlődését a 1960-as évek végétől kezdődően, amely azóta is igen aktív és népszerű kutatási terület (mátrixok közepeiről magyarul a [4] cikkben olvashatunk).

 

8. Zárás: további fizika a matematikában

Cikkünkben egy remélhetőleg sokak számára meglepő és érdekes példáját mutattuk annak, hogy tisztán matematikai jellegű állítások ‐ úgymint algebrai egyenlőtlenségek ‐ mögött is rejtőzhetnek fizikai elvek és törvények, amelyek egy csapásra szemléletessé és világossá tehetik az addig kissé száraznak tűnő összefüggéseket. Ahogy a bevezetőben is utaltunk rá, számtalan helyen találkozhatunk hasonló gyöngyszemekkel a matematikában, a már idézett [2] könyv rengeteg ilyen témakört tárgyal ‐ többek között a Pitagorasz-tételnek legalább fél tucat ,,fizikai bizonyítását'' mutatja be. Ezenkívül Pólya György kiváló [6] könyvében egy egész fejezetet szán a témakörre, valamint a [8] szakdolgozatban is bőven talál az Olvasó fizikai érveléseket matematikai eredményekre. További érdekes olvasnivalókat sorolunk fel az irodalomjegyzékben, ahol a legtöbb mű elektronikus változatának elérhetőségét is megadjuk (a linkek 2015. augusztusi állapotot tükröznek). Bízunk benne, hogy minél többen, diákok és tanárok egyaránt hasznát veszik majd a középiskolai matematikával és fizikával való foglalkozás során.

 

Hivatkozások

[1]	A. Lehman, A Resistor Network Inequality, SIAM Rev., 2 (1960), 152‐153. Elektronikus változat: http://www.jstor.org/stable/2027374.

[2]	M. Levi, The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, Princeton, New Jersey, 2009.

[3]	H. Minkowski, Geometrie der Zahlen, Teubner, Leipzig, 1896. Elektronikus változat: https://archive.org/details/geometriederzahl00minkrich.

[4]	Pálfia Miklós, Petz Dénes, Tsuyoshi Ando professzorról. Unitér dilatációk és mátrixok közepei, Polygon, XVI (2007), 1‐16. Elektronikus változat: http://www.renyi.hu/$\sim$petz/pdf/ando.pdf.

[5]	Pintér Lajos, Analízis I., Speciális matematika tankönyvek, Typotex, Budapest, 1998. Elektronikus változat: http://www.interkonyv.hu/konyvek/Analízis_1.

[6]	Pólya György, Indukció és analógia: A matematikai gondolkodás művészete I., Gondolat Kiadó, Budapest, 1988.

[7]	F. Reza, A. Lehman, A Resistor Network Inequality, SIAM Rev., 4 (1962), 150‐155. Elektronikus változat: http://www.jstor.org/stable/2028375.

[8]	Simon Júlia, Gondolkodjunk a fizika segítségével!, szakdolgozat, Eötvös Loránd Tudományegyetem, Budapest, 2014. Elektronikus változat: http://abesenyei.web.elte.hu/theses/simon.pdf.

[9]	G. Woeginger, When Cauchy and Hölder Met Minkowski: A Tour through Well-Known Inequalities, Math. Mag., 82 (2009), 202‐207. Elektronikus változat: http://www.jstor.org/stable/27765902