| Cím: | Gráfalgoritmusok 2. | |
| Szerző(k): | Schmieder László | |
| Füzet: | 2015/november, 481 - 484. oldal |  PDF | MathML PDF | MathML |
| Hivatkozás(ok): | 2015/október: Gráfalgoritmusok 1.
2016/május: Gráfalgoritmusok 7. 2016/március: Gráfalgoritmusok 5. 2016/április: Gráfalgoritmusok 6. 2016/február: Gráfalgoritmusok 4. 2015/december: Gráfalgoritmusok 3. | |
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az előző részben két csúcs között kerestünk útvonalat egy gráfban. Az ott megismert szélességi keresés a start csúcstól a cél csúcsig megtalál egy legrövidebb útvonalat, ha van út a két csúcs között. Amennyiben a keresés során nem adunk meg cél csúcsot, akkor a start csúcsból elérhető összes csúcsra kapunk egy legrövidebb útvonalat, vagyis bejárja a start csúcsból elérhető részgráfot. Az útvonal úgy áll elő, hogy a keresés során mindegyik érintett csúcshoz följegyezzük, hogy melyik szomszédjától értünk el hozzá. Mélységi bejárás rekurzívan(gráf, start) jártunk(csúcsok start kivételével) := nem honnan(minden csúcsra) := nem_létező_csúcs MBR(start) Mélységi bejárás rekurzívan vége MBR(csúcs) jártunk(csúcs) := igaz szomszéd := csúcs első szomszédja Ciklus amíg szomszéd létező csúcs Ha nem jártunk[szomszéd] akkor honnan(szomszéd) := csúcs MBR(szomszéd) Elágazás vége szomszéd := csúcs következő szomszédja Ciklus vége MBR vége A rekurzív megfogalmazás további előnye, hogy a visszalépésről nem kell külön gondoskodnunk: amikor egy csúcsból valamely szomszédos csúcson át elérhető részgráfot bejártuk, vagyis az MBR(szomszéd) eljárás lefutott, akkor a végrehajtás visszakerül a hívó ciklusba, és az adott csúcs következő, még el nem ért szomszédjánál folytatódik a bejárás. Példaként vegyünk egy irányított gráfot, melynek csúcsai 1-től 10-ig sorszámozottak, és a közöttük lévő kapcsolatokat az alábbi ábra szerintiek. Amennyiben a szomszédokat a sorszámuk szerint növekvő sorrendben vesszük, akkor az MBR(1) hívás először végigjárja az útvonalat, majd visszalépés után az részgráfot. 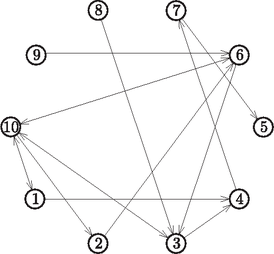 Az algoritmus nem rekurzív változatában minden csúcsnál megvizsgáljuk, hogy van-e még el nem ért szomszédja, vagy nincs. Az első esetben előre lépünk, a szomszéd lesz az aktuális csúcs, míg az utóbbi esetben visszalépünk ahhoz a szomszédhoz, ahonnan ide érkeztünk. Amikor egy szomszédból visszalépünk, akkor tudnunk kell, hogy melyik csúcsra kell visszalépnünk, valamint tudnunk kell, hogy annál a csúcsnál melyik a következő szomszéd, amelyet még érdemes vizsgálnunk. Ezt a két információt minden előrelépésnél meg kell őriznünk. A rekurzív algoritmusban ez automatikusan történt, mivel minden MBR eljáráshívás csúcs paramétere és szomszéd lokális változója egyedi minden hívásnál. A nem rekurzív algoritmusban nekünk kell gondoskodnunk az információk megőrzéséről. Mivel több előrelépés adatait is tárolnunk kell, és visszalépéskor mindig a legutolsó előrelépés adataira van szükség, ezért egy verem elnevezésű adatszerkezetet használunk föl. A vermet általában akkor alkalmazzuk, amikor az egymás után elhelyezett elemeket éppen fordított sorrendben szeretnénk fölhasználni. A szélességi keresésnél megismert sorhoz hasonlóan egyszerűen megvalósítható egy tömbbel és néhány változóval. Legyen a verem adatait tároló tömb v, mérete legyen méret, és mutasson az első üres helyre a tömbben. Ha a tömb 1-től sorszámozott, akkor az üres tömbnél vm értéke kezdetben 1. A verem szokásos műveletei: a verembe helyezés és a verem tetejéről egy elem kivétele, valamint annak vizsgálata, hogy a verem üres-e. Megvalósításuk egyszerű, a verembe helyezés például a következő: Verembe(elem) Ha vm <= méret akkor v[vm] := elem vm := vm 1 különben Hiba: nincs több hely a veremben Elágazás vége Verembe vége A mélységi bejárás nem rekurzív algoritmusát általában nem a fenti leírás szerint, hanem egyszerűbben valósítjuk meg. Az egyszerűsítés alapja az az ötlet, hogy ne a visszalépéshez szükséges adatokat helyezzük a verembe, hanem ‐ megfelelő sorrendben ‐ minden csúcsot, amelyet még nem látogattunk meg. A verem itt hasonlóan szerepet játszik, mint a szélességi bejárásnál a sor. Először az üres verembe helyezzük a start csúcsot, majd amíg a verem nem üres, addig a következőt ismételjük: kiveszünk egy csúcsot a veremből, és ha még nem jártunk ott, akkor megjelöljük, hogy már jártunk, és a verembe helyezzük az összes még föl nem keresett szomszédját. Így gyakorlatilag lecseréljük a verem tetején lévő, most elért csúcsot a még föl nem keresett szomszédjaira. Mivel mindig a verem tetejéről vesszük ki az utolsó oda rakott elemet, ezért a verembe korábban elhelyezett csúcsokhoz ‐ amelyek most a szomszédok alatt vannak ‐ később, csak a szomszédok és részgráfjaik bejárása után érünk el. Kivéve, ha egy szomszéd által kijelölt részgráfban egy korábban a verembe került csúcsot elérünk, de akkor az előbb is következik a mélységi bejárás során, tehát a veremből való kikerüléskor már nincs dolgunk vele. Mélységi bejárás(gráf, start) jártunk(csúcsok start kivételével) := nem honnan(minden csúcsra) := nem_létező_csúcs Verem_legyen_üres Verembe(csúcs) Ciklus amíg Verem nem üres Veremből(csúcs) Ha nem jártunk(csúcs) akkor jártunk(csúcs) := igaz szomszéd := csúcs első szomszédja Ciklus amíg szomszéd létező csúcs Ha nem jártunk(szomszéd) akkor Verembe(szomszéd) szomszéd := csúcs következő szomszédja Ciklus vége Elágazás vége Ciklus vége Mélységi bejárás vége Amennyiben a gráfot a legegyszerűbb módon, egy szomszédsági mátrixszal adjuk meg, akkor a szomszédokon egy egyszerű ciklussal végig lehet haladni, illetve könnyű megadni az első, vagy valamely szomszéd után következő szomszédot. Ha egy feladatban útvonalat keresünk egy gráfban a start csúcstól a cél csúcsig, akkor az előbbi két algoritmust úgy kell módosítanunk, hogy hagyják abba a keresést a cél csúcs megtalálásakor. A bejárás rekurzív MBR eljárását most érdemes függvénnyé alakítanunk, hogy visszaadja egy logikai érték formájában a keresés sikerességét. Mélységi keresés rekurzióval(gráf, start, cél) jártunk(csúcsok start kivételével) := nem honnan(minden csúcsra) := nem_létező_csúcs megvan_a_cél := MKR(start) Mélységi keresés rekurzióval vége MKR(csúcs) jártunk(csúcs) := igaz Ha csúcs cél Akkor MKR := igaz különben elértük_a_célt := hamis szomszéd := csúcs első szomszédja, ahol még nem jártunk Ciklus amíg nem igaz elértük_a_célt és szomszéd létező csúcs honnan(szomszéd) := csúcs elértük_a_célt := MKR(szomszéd) Ha még nem igaz elértük_a_célt akkor szomszéd := csúcs következő szomszédja, ahol még nem jártunk Elágazás vége Ciklus vége MKR := elértük_a_célt Elágazás vége MKR vége Ne tévesszük össze MKR két különböző jelentését az algoritmus-leíró nyelvben: a függvényhívás végét és az eredmény visszaadását pl. az MKR := elértük_a_célt utasítás jelöli, míg a függvényhívás formája MKR(szomszéd). Az eddig megismert algoritmusok segítséget nyújtanak egy gráf bejárásában, illetve egy útvonal megtalálásában. Természetesen nem mindig csak erre van szükség, de a bemutatott két bejárás alapját képezi több gráfokkal kapcsolatos algoritmusnak. Egy-egy konkrét probléma megoldásakor sokszor a fenti kétféle keresés módosított változatait alkalmazzuk. A következő részben bemutatunk gráfokkal modellezhető problémákat, melyek a fenti gráfkereső algoritmusokkal megoldhatók. 1. A mélységi keresésnél mi felel meg a görög mitológiából ismert Ariadné fonalának? 2. A szélességi keresés a start csúcstól egy legrövidebb utat talált a cél csúcsig. Igaz-e ez a mélységi keresésre is? 3. Tételezzük föl, hogy lefutott valamelyik keresés vagy bejárást végző algoritmus, és elkészítette a honnan táblázatot. Fogalmazzuk meg az útvonal kiírásának rekurzív és nem rekurzív algoritmusát. 4. Kövessük végig a fenti példában adott gráfon a mélységi bejárás nem rekurzív változatának működését az 1-es csúcstól indulva: észrevehetjük, hogy nem a rekurzív változatnak megfelelően járja be a gráfot. Miért? Hogyan kellene módosítani a nem rekurzív algoritmust, hogy tényleg pontosan egyformán haladjanak? 5. Legföljebb mekkora méretű veremre van szükség egy csúcsból álló gráf nem rekurzív mélységi bejárásához? Milyen az a gráf, amelynél ez a maximális méretű verem tele is lesz? 6. Készítsük el a mélységi keresés nem rekurzív változatát. |