Cím: Megoldásvázlatok a 2015/7. sz. emelt szintű matematika gyakorló feladatsorhoz
Szerző(k):  Sztranyák Attila 
Füzet: 2015/november, 461 - 468. oldal  PDF  |  MathML 

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. rész
 

 
1. Hány olyan 4 darab egész számból álló adatsokaság van, melynek mediánja 1, átlaga 2, szórásnégyzete pedig 3? Mi(k) ez(ek) az adatsokaság(ok)?  (12 pont)
 
Megoldás. Az adatsokaság elemei nemcsökkenő sorrendben legyenek a≤b≤c≤d. A medián 1, és ez most ‐ mivel páros számú adat van ‐ a két középső szám átlaga, ezért c=2-b.
Valamint az átlag miatt a négy szám összege a+b+(2-b)+d=8, ezért d=6-a. Vagyis az elemek a≤b≤2-b≤6-a. A szórásnégyzetre kapott feltétel miatt
3=(a-2)2+(b-2)2+(2-b-2)2+(6-a-2)24=2a2-12a+2b2-4b+244.
Innen 12=2a2-12a+2b2-4b+24. Ezt 2-vel osztva, és a jobb oldalon teljes négyzeteket kialakítva, végül rendezve, a 4=(a-3)2+(b-1)2 egyenlet adódik.
Mivel a és b egész számok, ezért a 4 két négyzetszám összege. Ez csak úgy lehet, ha 0=(a-3)2 és 4=(b-1)2, vagy fordítva, 4=(a-3)2 és 0=(b-1)2.
Az első esetben a=3 és |b-1|=2, amiből a 3;-1;3;3, illetve a 3;3;-1;3 adatnégyeseket kapjuk. Ezek egyike sem jó, mert a mediánjuk 3.
A második esetben |a-3|=2 (innen a=5 vagy a=1) és b=1 adódik. Mivel a≤b, ezért a=1. Az így kapott négy szám kielégíti a feltételeket.
Vagyis egyetlen megfelelő számnégyes van: 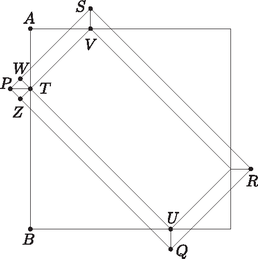1,1,1,5.
 
2. Egy 1 méter oldalhosszúságú, négyzet alakú asztallapra egy téglalap alakú abroszt terítünk. Az abrosz hosszabb oldalai kétszer olyan hosszúak, mint a rövidebbek, és úgy helyezzük az asztalra, hogy középvonalai egybeessenek az asztallap átlóival. Így az abrosz mind a négy sarka az asztallap síkjához képest 10 cm-rel lelóg. Az asztallap hány százalékát fedi a terítő ebben a helyzetben?  (13 pont)
 
Megoldás. A feladat során deciméterben fogunk számolni. Tekintsük az ábrát, ahol A, B az asztallap két csúcsa, P, Q, R, S a terítő csúcsai visszahajtva az asztallap síkjába, míg T, U, V a P, Q, S csúcsoknak az asztallap megfelelő oldaléleire vett merőleges vetületei.

 
 

Legyen a terítő két oldalának hossza PS=x, illetve PQ=2x, valamint AT=a. Ekkor TB=10-a.
A feladat szerint PT=QU=SV=1. Így a terítő elrendezése miatt
PZ=PW=12.
Ekkor
TV=x-2⋅12=x-2ésTU=2x-2⋅12=2x-2.
Az ATV és a BUT háromszögek egyenlő szárú derékszögű háromszögek, így TV=2a és TU=2(10-a)=102-2a. Innen a-ra és x-re a következő egyenleteket kapjuk: x-2=2a és 2x-2=102-2a. Az egyenleteket összeadva, majd mindkét oldalhoz 22-t adva: 3x=122, amiből x=42 adódik.
Vagyis a terítő oldalai 42 és 82 hosszúak.
Így a terítő teljes területe 42⋅82=64. Viszont az asztallapot nem fedi a négy saroknál lévő egybevágó egyenlő szárú, derékszögű háromszög. Ezek közül kettőt-kettőt együtt véve éppen két olyan négyzet kapható, melyek átlói 2 dm hosszúak. Így az abrosz asztallapot nem fedő részének a területe: 2⋅2⋅22=4.
Ezek szerint az abrosz az asztal 100 dm2-es területéből pontosan 60 dm2-t fed le, vagyis az abrosz az asztallapnak pontosan a 60%-át fedi le.
 
Megjegyzés. Mivel a terítő hosszabb oldala rövidebb az asztallap átlójánál (82<102), ezért valóban a fenti ábrán lerajzolt elrendezés valósul meg.
 
3. Oldjuk meg a következő egyenletet az egész (x;y) számpárok halmazán:
2x-2-8x+4=-|3y-25|.
 (14 pont)
 
Megoldás. A 8x+4 miatt -12≤x, és mivel x egész, ezért legalább 0. A bal oldalt átalakítva:
(2x+1)-22x+1-3=(2x+1)-22x+1+1-4.
Ez utóbbit 2x+1-ben teljes négyzetté alakítva az egyenletünk a következő alakra hozható:
(2x+1-1)2-4=-|3y-25|.
Mivel a jobb oldal nem pozitív, a bal sem lehet az. Vagyis (2x+1-1)2≤4, innen |2x+1-1|≤2, vagyis -1≤2x+1≤3. Innen 2x+1≤9, végül x≤4 adódik. Vagyis x lehetséges értékei 0, 1, 2, 3 és 4.
Helyettesítsük be ezeket az értékeket rendre az egyenlet bal oldalába.
Az x=1, x=2 és x=3 esetén a bal oldal értéke irracionális. Mivel a jobb oldal racionális (hiszen y egész), ezek nem adnak megoldásokat.
Ha x=0, akkor a bal oldal értéke: 0-2-0+4=-4. Ekkor 4=|3y-25|, tehát vagy 4=3y-25, amiből y=223, ami nem megoldás; vagy -4=3y-25, amiből y=-6, ami megoldás.
Ha x=4, akkor a bal oldal értéke: 8-2-32+4=0. Ekkor 0=|3y-25|, vagyis y=23, ami szintén nem megoldás.
Összesen egyetlen megfelelő számpár van, és ez az x=0, y=-6.
 
4. Az f(x)=x függvény grafikonját elmetsszük az x=b egyenletű függőleges egyenessel. Az egyenes, f(x), és az x-tengely által bezárt S síkidom területe t=18.
a) Mennyi b pontos értéke?
b) Az S síkidomot megforgatjuk az x-tengely körül. Mekkora a keletkezett forgástest térfogata?  (12 pont)
 
Megoldás. a) A kérdéses terület számolható integrál segítségével:
T=18=∫0bxdx=∫0bx12dx=[23⋅x32+c]0b=23⋅b32,innen  27=b32,  végül  b=9.

b) A kérdéses térfogat:
V=π∫0bf2(x)dx=π∫09xdx=π[12⋅x2+c]09=812π≈127,23.

 

II. rész
 

 
5. a) Igazoljuk, hogy az x3+3x2-3x-1=0 egyenletnek van egyjegyű pozitív egész megoldása.
b) Oldjuk meg az x3+3x2-3x-1=0 egyenletet a valós számok halmazán.
c) Adjuk meg a tangensra vonatkozó addíciósképletek és nevezetes szögek szögfüggvényei segítségével a 105∘ és a 165∘ szögek tangenseinek a pontos értékét.
d) Oldjuk meg a következő egyenletet a valós számok halmazán:
(tgx+2)2=7+tgx+ctgx.
 (16 pont)
 
Megoldás. a) Az x=1 megoldás, ez behelyettesítéssel ellenőrizhető. (A racionális gyökteszt mutatja, hogy nem is lehet más pozitív egész megoldás.)
b) Mivel x=1 megoldása az egyenletnek, az egyenlet bal oldala felírható
x3+3x2-3x-1=(x-1)(ax2+bx+c)
alakban alkalmas a, b, c valós konstansokkal.
Két polinom akkor egyezik meg, ha együtthatóik rendre azonosak. Így
(x-1)(ax2+bx+c)=ax3+(b-a)x2+(c-b)x-c=1⋅x3+3⋅x2-3⋅x-1
miatt rendre a=1, b=4, c=1 adódik.
Az egyenletet (x-1)(x2+4x+1)=0 szorzatalakra hozva a bal oldal második tényezőjéből adódik, hogy x2=-2-3, illetve x3=-2+3 az egyenlet két irracionális gyöke a korábban megtalált x1=1 mellett.
c) Felhasználva a tg45∘=1, tg60∘=3 és tg120∘=-3 értékeket, valamint a következő addíciós képletet:
tg(α+β)=tgα+tgβ1-tgα⋅tgβ,
kapjuk:
tg105∘=tg(45∘+60∘)=1+31-1⋅3=(1+3)2(1-3)(1+3)=4+23-2=-2-3.
Hasonlóan:
tg165∘=tg(45∘+120∘)=1-31-1⋅(-3)=(1-3)2(1+3)(1-3)=4-23-2==-2+3.

d) A tgx és ctgx függvények értelmezési tartománya miatt x≠k⋅π2 (k∈Z), ugyanezen okokból sem tgx, sem ctgx nem lehet 0.
Elvégezve a zárójelfelbontást, és rendezve az egyenletet: tg2x+3tgx-3-ctgx=0 adódik. Innen tgx(=1ctgx≠0)-szel szorozva a tg3x+3tg2x-3tgx-1=0 egyenletet kapjuk. Ez tgx helyére új változót bevezetve az új változóban éppen a b)-beli egyenlet. Vagyis (tgx)1,2,3=-2-3;-2+3;1.
A c) pontot figyelembe véve, rendre megoldva az egyenleteket: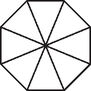
hatgx=-2-3,akkor  x1=7π12+k⋅π(k∈Z);hatgx=-2+3,akkor  x2=11π12+l⋅π(l∈Z),   végülhatgx=1,akkor  x3=π4+m⋅π(m∈Z)   adódik megoldás gyanánt.

 
6. Egy szabályos nyolcszögbe az ábra szerint a középpontján keresztül nyolc egyforma egyenlő szárú háromszöget rajzolunk be.

 
 

a) Mekkora a háromszögek súlypontjai által meghatározott szabályos nyolcszög, illetve az eredeti nyolcszög területének az aránya?
b) Kati az ábrának megfelelő pörgettyűket csinál. A pörgettyűk felső felén lévő nyolc kis háromszög mindegyikét kifesti a piros, fehér, vagy zöld színek valamelyikével (a pörgettyű alját nem festi le).
Hányféle különböző pörgettyűt készíthet Kati, ha az élben szomszédos háromszögek színét különbözőnek szeretné, de nem ragaszkodik ahhoz, hogy mind a három színt felhasználja?  (16 pont)
 
Megoldás. a) Vegyük az eredeti nyolcszög köré írható körének sugarát R=1-nek (ez megtehető).
Az ábrán lévő háromszögek olyan egyenlő szárú háromszögek, melyeknek alapjukkal szemközt 45∘-os szöge van. Egy ilyen háromszög alapjának magassága egyben súlyvonal is, valamint a 45∘-os csúcsszöget felezi. A csúcstól a súlypontig terjedő szakasz a magasság-súlyvonalnak a 2/3-a, ez az új nyolcszög köré írható körének sugara.
Ezek alapján az új nyolcszög köré írható körének sugara
r=cos22,5∘⋅23=2+23≈0,616.
Ez a hasonlóság aránya. Ennek négyzete a kérdéses területek aránya, vagyis
tújTrégi=2+29≈0,379.

b) A feladat szövege alapján az egymásba forgatható pörgettyűk azonosnak tekintendőek.
b1) Ha csak két színt használunk fel, és rögzítjük melyik ez a két szín, akkor csak egyféle pörgettyűt tudunk csinálni (hiszen felváltva kell szerepelni a két színnek a festett háromszögek között.) A felhasznált két színt (vagy a nem felhasznált egyet) háromféleképpen választhatjuk ki. Tehát itt 3 eset van.
b2) Ha mind a három szín szerepel, akkor ‐ aszerint, hogy az egyes színeket hányszor használjuk ‐ a következő esetek lehetnek: 4,3,1 / 4,2,2 / 3,3,2.
b21) A ,,4,3,1'' eset. Azt a színt, amelyikből 4 háromszög van 3-féleképpen, amiből 1 van, már csak 2-féleképpen választhatjuk, vagyis színeket 6-féleképpen választhatunk.


 

b21)
 

Ha már kiválasztottuk, hogy melyik színből mennyi lesz, akkor viszont már csak egyféle pörgettyű készíthető, hiszen amelyik színből 4 van, azt csak úgy tehetjük le, hogy minden két ilyen színű háromszög között pontosan egy másféle színű háromszög található. A másmilyen színek pedig a forgatás miatt csak egyféleképp ,,helyezhetők el''.
Tehát itt összesen 6 eset lehetséges.
b22) A ,,4,2,2'' eset. Azt a színt, amelyikből 4 háromszög van 3-féleképpen választhatjuk. Vagyis színeket most csak 3-féleképpen választhatunk.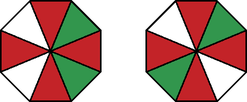


 

b22)
 

Ha már kiválasztottuk, hogy melyik színből mennyi lesz, akkor azt a színt, amelyikből 4 van, most is csak egyféleképpen tehetjük le. A két egyforma színből az egyik fajtát a maradék négy helyre kétféleképpen is tehetjük. Vagy úgy, hogy egy háromszög legyen közöttük, vagy úgy, hogy egymással szemben legyenek (lásd az ábrákat). Vagyis itt 3⋅2=6 eset lehetséges.
b23) A 3,3,2 eset. Azt a színt, amelyikből 2 háromszög van 3-féleképpen választhatjuk. Vagyis színeket megint csak 3-féleképpen választhatunk.
Ha pl. a pirosból van kettő, akkor három lehetőség van aszerint, hogy a két piros háromszög között 1, 2, vagy 3 háromszög kap más színt. Vizsgáljuk meg ezeket rendre.
b231) Ha a két piros között egy háromszög más színű. Ennek a háromszögnek a színét 2 szín közül választhatjuk. Ha viszont már választottunk (legyen pl. zöld), akkor a maradék 5 színezetlen háromszög közül 3 ‐ a zöldtől különböző ‐ azonos szín van még, ami csak egyféleképpen színezhető jól. Vagyis itt összesen 2 eset lehetséges.


 

b231)
 

b232) Ha a két piros között két háromszög más színű. Ezen két háromszögnek a színét 2-féleképpen választhatjuk ki. Hasonlóan a maradék 4 színezetlen háromszög is kétféleképpen színezhető. Vagyis itt a színek figyelembevételével 2⋅2=4 eset lehetséges.


 

b232)
 

b233) Ha a két piros egymással átellenes. Itt (látszólag) két eset van (felülről az óramutató járásával egyezően indulva): PZFZPFZF és PFZFPZFZ. Ezek viszont egy 180 fokos forgatással egymásba forgathatóak. Vagyis itt 1 eset van. A ,,3,3,2'' esetben tehát 3⋅(2+4+1)=21 lehetőség van a színezésre.


 

b233)
 

Vagyis 3+6+6+21=36-féleképpen színezhető ki a pörgettyű.
 
7. a) Adjuk meg a P(-1;1), és Q(3;3) pontokon átmenő e egyenes egyenletét.
b) Az f(x)=x2-6x+8 egyenletű függvény grafikonjának melyik az a pontja, amelyikbe húzott érintő merőleges a fenti e=PQ egyenesre?
c) Adjuk meg az e egyenes, az érintő, illetve a két koordináta-tengely által bezárt (az első síknegyedbe eső) konvex négyszög területét.  (16 pont)
 
Megoldás. a) A P-ből Q-ba mutató v=(4;2) irányvektor alapján az egyenes meredeksége 12. Emiatt az y-tengelyt 32-nél metszi, vagyis a PQ egyenes egyenlete: y=x+32.
b) Az érintő pontosan akkor merőleges az iménti egyenesre, ha meredekségeik szorzata -1. Mivel a PQ egyenesének meredeksége 12, így az érintő meredeksége -2.
Szükség van még az érintő egy pontjára. Ez például deriválással meghatározható. Az f(x)=x2-6x+8 függvény tetszőleges P0=(x0;f(x0)) pontjába húzott érintő meredeksége éppen f'(x0)=2x0-6. Ennek kell -2-nek lennie. Innen x0=2, és így P0=(2;0) adódik az érintési pontra.
c) Foglaljuk az eddigieket egy ábrába. Az érintési ponton átmenő -2 meredekségű érintő egyenlete: y=-2x+4. Nekünk az OP0RS négyszög területe kell.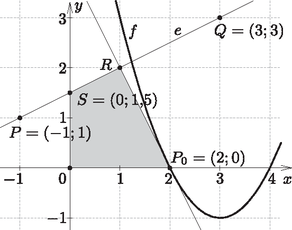

 
 

Az R pont az y=-2x+4 és az y=x+32 egyenesek közös pontja. Az egyenletek jobb oldalát egyenlővé téve -2x+4=x+32, majd x=1, és innen y=2. Vagyis R koordinátái: R(1;2).
Innen az OP0RS négyszög területe gyorsan meghatározható. Például az OP0TV 2 oldalhosszú négyzet (ahol T(2;2), V(0;2)) területéből kivonva a megfelelő 14, illetve 1 területű, az OP0RS-hez nem tartozó derékszögű háromszögek területét, a kérdéses terület:
TOP0RS=4-1-14=114.

 
8. Egy téglatest térfogata 8cm3. Ha a téglatest minden élét 1 centiméterrel megnöveljük, akkor egy 27cm3 térfogatú téglatestet kapunk. Mekkora térfogatú téglatestet kapunk, ha ismét megnöveljük az éleket 1-1 centiméterrel?  (16 pont)
 
Megoldás. Jól látszik, hogy az eredeti téglatest lehet egy 2 cm élhosszú kocka. Kérdés az, hogy lehet-e más. Legyenek az eredeti téglatest egy csúcsba futó élei az a, b, c pozitív számok. Ekkor abc=8 az eredeti térfogat.
Kétszer alkalmazzuk a háromtagú számtani-, és mértani közép közötti összefüggést. Először:
2=83=abc3≤a+b+c3,vagyis6≤a+b+c,
és egyenlőség csak az  a=b=c=2 esetben lehetséges. Másodszor:
4=823=a2b2c23=ab⋅ac⋅bc3≤ab+ac+bc3,vagyis12≤ab+ac+bc,
és egyenlőség csak az a=b=c=2 esetben lehetséges. Az új térfogatra kapott feltétel szerint:
27=(a+1)(b+1)(c+1)=abc+ab+ac+bc+a+b+c+1≥8+12+6+1=27.
Ez nyilván csak úgy lehet, ha 6=a+b+c és 12=ab+ac+bc egyaránt teljesül, vagyis, ha az eredeti téglatest kocka.
Azaz valóban csak a 2 cm élű kocka lehetett az eredeti test.
Így az újabb növelés után kapott téglatest térfogata: 43=64(cm3).
 
9. Egy játékgyártó vállalat az ábrának megfelelő műanyag játékkockákat gyárt. A gyártás során elkészítik a ,,sértetlen'' 2 cm élhosszú kockákat, majd a nyolc csúcs mindegyikénél az éleken kimérve az azonos d távolságokat levágnak egy-egy olyan tetraédert, melynek alaplapja szabályos háromszög. A levágott tetraéderek anyagát összegyűjtik, és ebből a hulladékanyagból később új játékkockákat gyártanak. (Ezek hulladékát is összegyűjtik. Általában nem kell anyagveszteséggel számolnunk a gyártás során, illetve a hulladékot nem keverik a nem hulladék anyaggal össze.)

 
 

a) Mekkora a d távolság pontos értéke, ha pontosan 48 darab játékkocka hulladékából állítható elő egy, mind a nyolc csúcsában ép 2 cm élhosszú kocka?
b) A nem hulladékanyagból készült kockák mind első osztályúak a minőség szempontjából, míg a hulladékból készült kockáknak csak 80%-a első osztályú, a többi hibás. A gyártó cég 20 éve változatlan feltételekkel, változatlan gyártósoron gyártja játékait. A hulladék- és a nem hulladékanyagból készült kockák a gyártás során egy tárolóba kerülnek, ahol összekeverednek. A jubileum alkalmából egy exkluzív 200 darabos játékkocka szettet adnak ki díszdobozba csomagolva. Mekkora az esélye, hogy a dobozba legalább két darab hibás dobókocka kerül?  (16 pont)
 
Megoldás. a) Egy levágott kis tetraéder térfogata:
V=d⋅d⋅d23=d36.
Vagyis a hulladék mennyisége egy kockánál: 8d36. A szöveg alapján:
48⋅8d36=64d3=23,innen  d3=18,   és végül  d=12.
Vagyis a kérdéses d távolság éppen 5 mm.
b) Legyen pontosan 48 ép kockára való anyagunk. Abból legyárthatunk 48 csonkolt dobókockát, és azok maradékából pontosan egy újabb ép kockát kapunk. Vagyis 48 ép egységnyi anyagból 1 ép egységnyi maradék keletkezik. Mivel nem kell anyagveszteséggel számolni, a gyártás során felhasznált teljes anyagmennyiség 148 része készül hulladék anyagból.1 Az összes kocka
148⋅15=1240
része hibás, és így 239240 eséllyel első osztályú egy játékkocka.
Számoljuk ki a komplementer esetet, vagyis azt, hogy mekkora az esély arra, hogy pontosan 0 vagy 1 darab hibás kocka van:
P(0  hibás)=(239240)200≈0,4338,illetveP(1  hibás)=(2001)⋅(239240)199⋅(1240)1=200⋅239199240200≈0,3630.
Annak az esélye, hogy pontosan 0 vagy 1 darab kocka hibás, kb. 0,4338+0,3630=0,7968, azaz annak a valószínűsége, hogy a szettben legalább két darab hibás játékkocka van, körülbelül 20,32%.
1Húsz éve változatlan feltételekkel gyártják a kockákat, tehát tekinthetjük úgy, hogy a kockagyártás folyamata hosszú távú, rendszeresen érkezik friss nyersanyag, és az összes hulladék felhasználásra kerül.